- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамикалық қатарлар презентация
Содержание
- 1. Динамикалық қатарлар
- 2. Дәріс жоспары: Динамикалық қатарлардың түрлері. Тренд түсінігі.
- 3. Динамиқалық қатардың анықтамасы Динамикалық (уақытты) қатар –
- 4. Динамикалық қатарға мысал Стат. көрсеткіш (у)
- 5. Динамикалық қатарлардың түрлері
- 6. Моенттік динамикалық қатарлар зерттелетін құбылыс өлшемдерінің белгілі
- 7. Толық динамикалық қатарлардың аралығы бірдей болады.
- 8. Абсолютті мәндердің қатарлары – қатар деңгейі сәйке
- 9. Дәріс жоспары: Динамикалық қатарлардың түрлері. Тренд түсінігі.
- 10. Тренд түсінігі Тренд – бұл уақыт ішінде
- 11. Ең кіші квадраттар әдісі Зерттелетін құбылыстың өзгерісін
- 12. Түзу сызықты
- 13. Сызықты тренд теңдеуі Егер зерттелетін динамикалық қатардың
- 15. Бұл теңдеуге «t»-ның мәндерін қою арқылы теүзетілген
- 16. Дәріс жоспары: Динамикалық қатардың түрлері. Тренд түсінігі.
- 17. Динамикалық қатарларды болжау Динамикалық қатардың болжанатын
- 18. Іс жүзінде болжанатын құбылыстарды экстраполяциялаудың нәтижесі әдетте
- 19. Аралықтардың шекараларын анықтау үшін формуласы қолданыдады.
- 20. 1 мысал. Берілген динамикалық қатар негізінде: ауруға
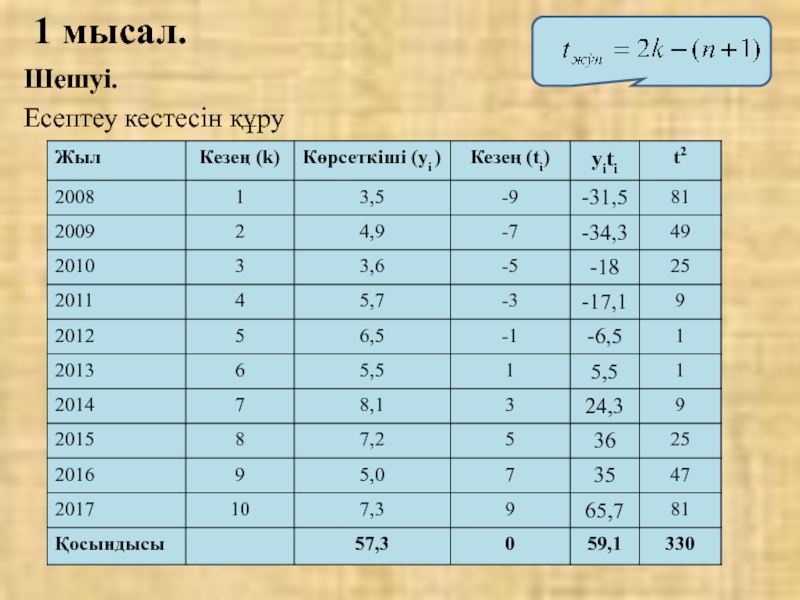
- 21. Шешуі. Есептеу кестесін құру 1 мысал.
- 22. Шешуі (жалгасы). Сызықты тренд теңдеуінің коэффициенттерін
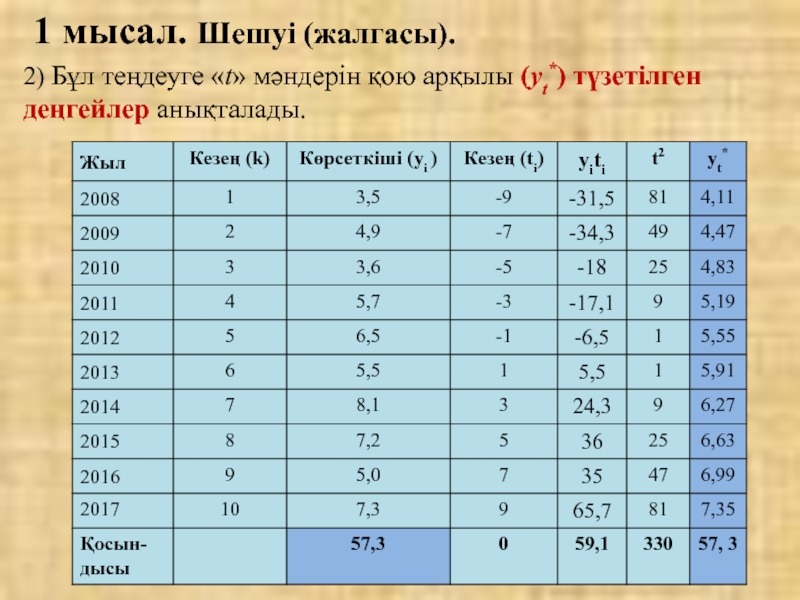
- 23. 2) Бұл теңдеуге «t» мәндерін қою арқылы (уt*) түзетілген деңгейлер анықталады. 1 мысал. Шешуі (жалгасы).
- 24. Cызбада динамикалық қатардың деңгейі бойынша түзетілген теориялық
- 25. 3) 2018 жылы болжам 95% сенім ықтималдығы
- 26. t=11 уақытында динамикалық қатардың деңгейінің болжамған мәнінің
- 27. Стьюдент t-белгісінің критикалық мәндерінің кестесі
- 28. Дәріс жоспары: Динамикалық қатардың түрлері. Тренд түсінігі.
- 29. Динамикалық қатардың көрсеткіштері Құбылыстың уақыт ішіндегі дамуының
- 30. Мұндай көрсеткіштерге жататындар: абсолюттік өсу;
- 31. Тұрақты базалық (базистік) динамикалық көрсеткіштер базалық деңгей
- 32. Абсолютті өсу (Δi) – динамикалық қатардың екі
- 33. Абсолютті өсу (Δi) Динамикалық қатардың көрсеткіштері
- 34. Ұлғаю коэффициенті (ki) екі салыстырмалы деңгейдің қатынасы
- 35. Ұлғаю коэффициенті (ki) Динамикалық қатардың көрсеткіштері
- 36. Егер өсудің коэффициенттері пайызбен өрнектелген болса, онда
- 37. Ұлғаю шапшаңдығы (Тұлғаю) Динамикалық қатардың көрсеткіштері
- 38. Өсу шапшаңдығы берілген кезең деңгейінің базистік деңгейден
- 39. Өсу шапшаңдығы (Төсу) Динамикалық қатардың көрсеткіштері
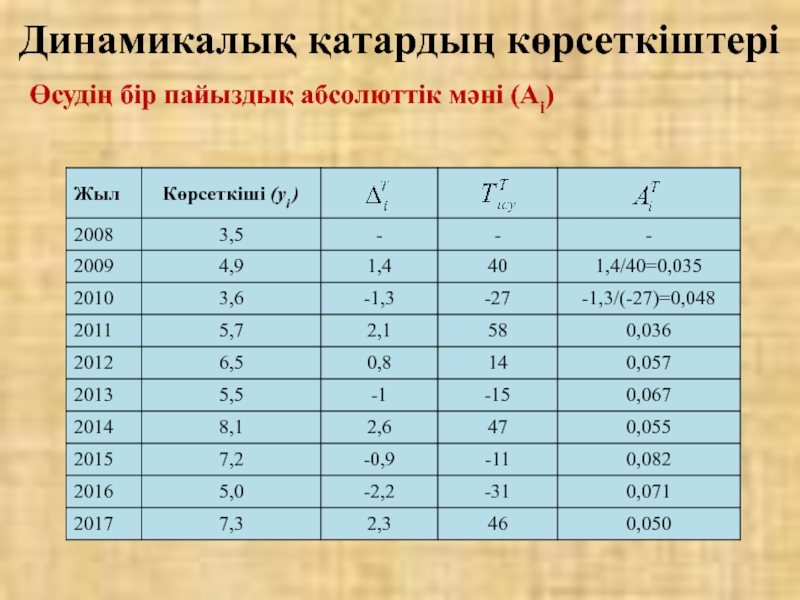
- 40. Өсудің бір пайыздық абсолюттік мәні (Аi) алынған
- 41. Өсудің бір пайыздық абсолюттік мәні (Аi) Динамикалық қатардың көрсеткіштері
- 42. Зерттелетін құбылыстың динамикасын жалпы сипаттауда кезең қатары
- 43. Ұлғаюдың орташа шапшаңдығы – бұл динамикалық қатар
- 44. Өсудің орташа шапшаңдығы келесі формуламен есептелінеді: Динамикалық қатардың көрсеткіштері
- 45. Бақылау сұрақтары: Динамикалық қатар дегеніміз не? Ол
Дәріс жоспары: Динамикалық қатарлардың түрлері. Тренд түсінігі. Динамикалық қатарларды түзету әдістері. Динамикалық қатарларды болжау. Динамикалық қатардың көрсеткіштері.
Слайд 2Дәріс жоспары:
Динамикалық қатарлардың түрлері.
Тренд түсінігі. Динамикалық қатарларды түзету әдістері.
Динамикалық қатарларды
болжау.
Динамикалық қатардың көрсеткіштері.
Динамикалық қатардың көрсеткіштері.
Слайд 3Динамиқалық қатардың анықтамасы
Динамикалық (уақытты) қатар – бірнеше реттелген кезеңдердің немесе периодттардың
қандайда бір мәндерінің көрсеткіштерінің жиыны.
Кез келген уақытты қатар екі элементтен:
келтірілген статистикалық берілгендерге жататын уақыт моментінен немесе кезеңдерінен (ti) тұрады;
зертелетін нысанды белгілі бір моментте немесе көрсетілген уақыт кезеңінде сипаттайтын статистикалық көрсеткіштерінен немесе қатардың деңгейінен (yi) тұрады.
Кез келген уақытты қатар екі элементтен:
келтірілген статистикалық берілгендерге жататын уақыт моментінен немесе кезеңдерінен (ti) тұрады;
зертелетін нысанды белгілі бір моментте немесе көрсетілген уақыт кезеңінде сипаттайтын статистикалық көрсеткіштерінен немесе қатардың деңгейінен (yi) тұрады.
Слайд 4Динамикалық қатарға мысал
Стат. көрсеткіш (у)
Уақыт моменттері немесе кезеңдері (ti)
Қатардың деңгейлері (уi)
Слайд 5
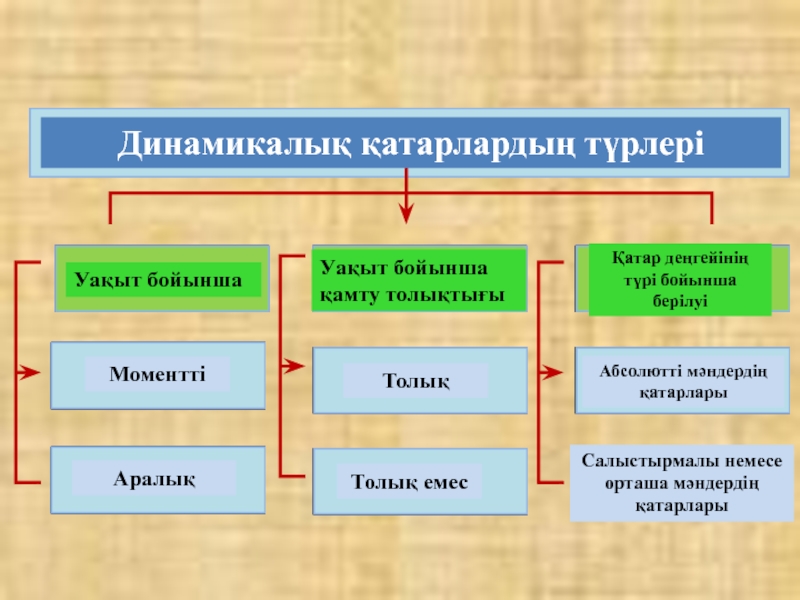
Динамикалық қатарлардың түрлері
Уақыт бойынша
Уақыт бойынша қамту толықтығы
Қатар деңгейінің түрі бойынша берілуі
Моментті
Аралық
Толық
Толық емес
Абсолютті мәндердің қатарлары
Салыстырмалы немесе орташа мәндердің қатарлары
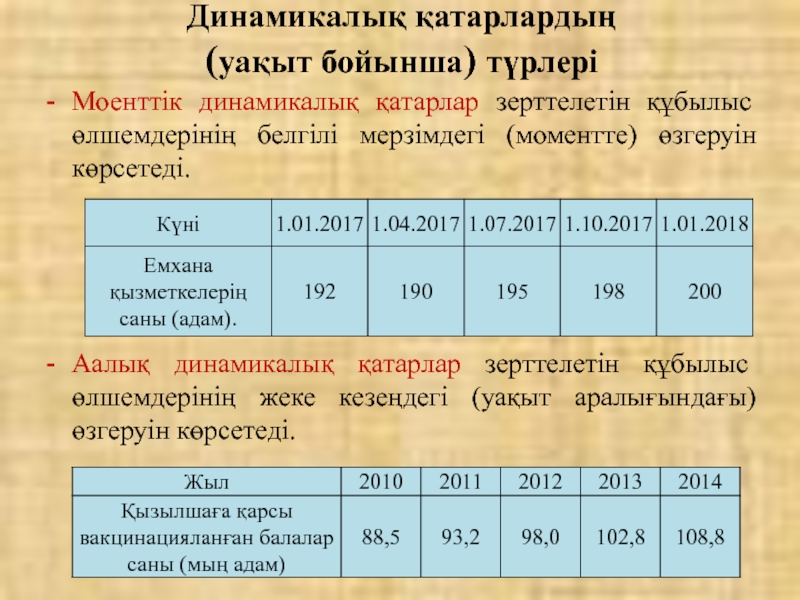
Слайд 6Моенттік динамикалық қатарлар зерттелетін құбылыс өлшемдерінің белгілі мерзімдегі (моментте) өзгеруін көрсетеді.
Аалық динамикалық қатарлар зерттелетін құбылыс өлшемдерінің жеке кезеңдегі (уақыт аралығындағы) өзгеруін көрсетеді.
Динамикалық қатарлардың
(уақыт бойынша) түрлері
Слайд 7Толық динамикалық қатарлардың аралығы бірдей болады.
Толық емес динамикалық қатарлардың аралығы
бірдей болмайды.
Динамикалық қатарлардың (уақыт ішінде қамту толықтығы бойынша) түрлері
Слайд 8Абсолютті мәндердің қатарлары – қатар деңгейі сәйке (кг, л, км, сағ,
тг және т.б.) өлшем бірліктерімен беріледі.
Салыстырмалы мәндердің қатарлары – қатар деңгейі сәйкес пайыз, бөліктер, промиллелер және т.б. түрінде беріледі.
Орташа мәндердің қатарлары – қатар деңгейі орташа көрсеткіштер болып табылатын сандармен беріледі.
Салыстырмалы мәндердің қатарлары – қатар деңгейі сәйкес пайыз, бөліктер, промиллелер және т.б. түрінде беріледі.
Орташа мәндердің қатарлары – қатар деңгейі орташа көрсеткіштер болып табылатын сандармен беріледі.
Динамикалық қатарлардың (қатар деңгейінің түрі бойынша берілуі) түрлері
Слайд 9Дәріс жоспары:
Динамикалық қатарлардың түрлері.
Тренд түсінігі. Динамикалық қатарларды түзету әдістері.
Динамикалық қатарларды
болжау.
Динамикалық қатардың көрсеткіштері.
Динамикалық қатардың көрсеткіштері.
Слайд 10Тренд түсінігі
Тренд – бұл уақыт ішінде көрсеткіштер дамуының негізгі үрдісін анықтайтын,
уақыттан алынған функция.
Трендті орнату үшін динамикалық қатар түзетіледі.
Түзету келесі тәсілдермен іске асырылады:
кезеңдерді ірілендіру;
топтық орташаны есептеу;
жылжымалы орташаны есептеу;
ең кіші квадраттар әдісі.
Трендті орнату үшін динамикалық қатар түзетіледі.
Түзету келесі тәсілдермен іске асырылады:
кезеңдерді ірілендіру;
топтық орташаны есептеу;
жылжымалы орташаны есептеу;
ең кіші квадраттар әдісі.
Слайд 11Ең кіші квадраттар әдісі
Зерттелетін құбылыстың өзгерісін (динамикасын) дәл сапалы бағалау үшін
ең кіші квадраттар әдісі қолданылады:
мұндағы, уi - нақты (эмпирикалық) қатар деңгейі,
уt* - теориялық қатар деңгейі.
Трендтің әртүрлі үлгілерін (модель) (сызықты, параболалық, экпоненциалды және т.б.) құруға болады.
Үлгіні таңдау зерттеудің мақсатына байланысты болады және ол теориялық талдауға сәйкес негізделген болуы керек.
мұндағы, уi - нақты (эмпирикалық) қатар деңгейі,
уt* - теориялық қатар деңгейі.
Трендтің әртүрлі үлгілерін (модель) (сызықты, параболалық, экпоненциалды және т.б.) құруға болады.
Үлгіні таңдау зерттеудің мақсатына байланысты болады және ол теориялық талдауға сәйкес негізделген болуы керек.
Слайд 12Түзу сызықты
теңдеу (сызықты тренд) құбылыстың дамуын айқындайтын үрдістің қарапайым үлгісі болып табылады.
Мұндағы «а» және «b» – коэффициенттер, олар төмендегі формулалар бойынша есептелінеді:
Мұндағы «а» және «b» – коэффициенттер, олар төмендегі формулалар бойынша есептелінеді:
Ең кіші квадраттар әдісі
Слайд 13Сызықты тренд теңдеуі
Егер зерттелетін динамикалық қатардың есептеу уақытын, уақыт көрсеткіштерінің қосындысын
нөлге тең болатындай етіп алса, онда теңдеулердің (a және b) параметрлерін анықтайтын жеңілдетілген формулалар алуға болады:
егер қатарда тақ сандар болса
егер қатарда жұп сандар болса
мұндағы k – жылдың реттік нөмірі,
n – кезеңдегі жылдардың саны.
егер қатарда тақ сандар болса
егер қатарда жұп сандар болса
мұндағы k – жылдың реттік нөмірі,
n – кезеңдегі жылдардың саны.
Слайд 14 болғанда сызықты тренд
теңдеуінің коэффици-
енттерін табу үшін , формулалары қолданылады.
Трендтік үлгі болып табылатын анықталатын функцияның есептелген параметрлеріне сәйкес, қажетті динамикалық қатар үшін түзу сызықты теңдеудің жазылуы:
енттерін табу үшін , формулалары қолданылады.
Трендтік үлгі болып табылатын анықталатын функцияның есептелген параметрлеріне сәйкес, қажетті динамикалық қатар үшін түзу сызықты теңдеудің жазылуы:
Сызықты тренд теңдеуі
Слайд 15Бұл теңдеуге «t»-ның мәндерін қою арқылы теүзетілген деңгейледі (уt*) табуға болады.
Егер
есептеулер дұрыс орындалса, онда эмпирикалық қатардың мәндерінің қосындысы түзетілген қатардың есептелген деңгейлерінің қосындысымен сәйкес келуі керек, яғни
Сызықты тренд теңдеуі
Слайд 16Дәріс жоспары:
Динамикалық қатардың түрлері.
Тренд түсінігі. Динамикалық қатарларды теңестіру әдістері.
Динамикалық қатарларды
болжау.
Динамикалық қатардың көрсеткіштері.
Динамикалық қатардың көрсеткіштері.
Слайд 17Динамикалық қатарларды болжау
Динамикалық қатардың болжанатын мәндерінің деңгейін анықтау үшін экстраполяция
әдісі қолданылады.
Экстраполяция зерттелген қатардан тыс деңгейлерді табу, яғни өткен кезеңде байқалып отырған үрдістің болашағын кеңейту.
Экстраполяция зерттелген қатардан тыс деңгейлерді табу, яғни өткен кезеңде байқалып отырған үрдістің болашағын кеңейту.
Слайд 18Іс жүзінде болжанатын құбылыстарды экстраполяциялаудың нәтижесі әдетте аралық бағалар түрінде алынады
- бұл болжамның сенімді аралығы.
Динамикалық қатарларды болжау
Слайд 19Аралықтардың шекараларын анықтау үшін
формуласы қолданыдады.
мұндағы -
«t» уақыт кезіндегі қатар деңгейінің болжанған мәнінің дәл бағасы, S – трендтен қалдық орташа квадраттық ауытқу.
мұндағы n – динамикалық қатар деңгейлерінің саны,
m – тренд үлгісінің параметрлерінің саны (сызықты үшін m=2),
tр - маңыздылық деңгейі р=0,05 болғандағы Студенттің үлестіріміне сәйкес және еркіндік дәрежесі f=n-m болғандағы сенімділік коэффициенті.
мұндағы n – динамикалық қатар деңгейлерінің саны,
m – тренд үлгісінің параметрлерінің саны (сызықты үшін m=2),
tр - маңыздылық деңгейі р=0,05 болғандағы Студенттің үлестіріміне сәйкес және еркіндік дәрежесі f=n-m болғандағы сенімділік коэффициенті.
Динамикалық қатарларды болжау
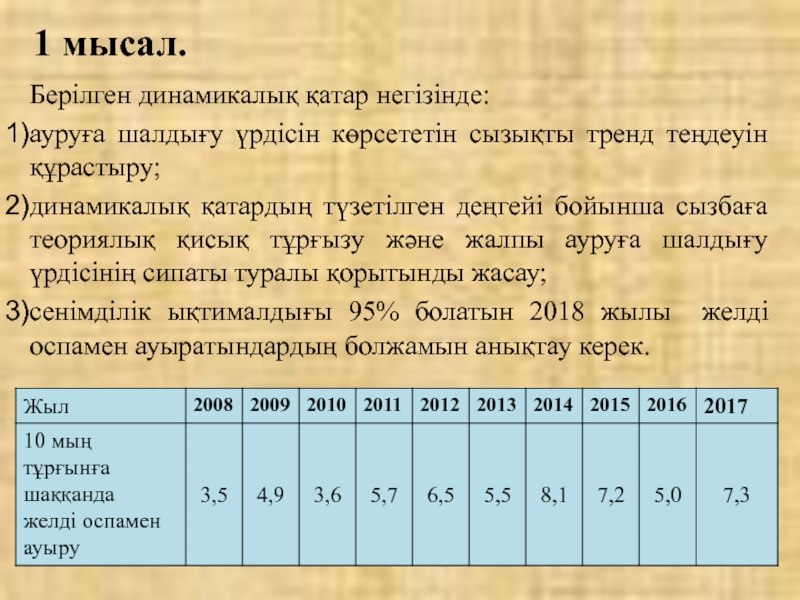
Слайд 201 мысал.
Берілген динамикалық қатар негізінде:
ауруға шалдығу үрдісін көрсететін сызықты тренд теңдеуін
құрастыру;
динамикалық қатардың түзетілген деңгейі бойынша сызбаға теориялық қисық тұрғызу және жалпы ауруға шалдығу үрдісінің сипаты туралы қорытынды жасау;
сенімділік ықтималдығы 95% болатын 2018 жылы желді оспамен ауыратындардың болжамын анықтау керек.
динамикалық қатардың түзетілген деңгейі бойынша сызбаға теориялық қисық тұрғызу және жалпы ауруға шалдығу үрдісінің сипаты туралы қорытынды жасау;
сенімділік ықтималдығы 95% болатын 2018 жылы желді оспамен ауыратындардың болжамын анықтау керек.
Слайд 22Шешуі (жалгасы).
Сызықты тренд теңдеуінің коэффициенттерін анықтау:
Сызықтық тренд теңдеуі:
1 мысал.
Слайд 232) Бұл теңдеуге «t» мәндерін қою арқылы (уt*) түзетілген деңгейлер анықталады.
1
мысал. Шешуі (жалгасы).
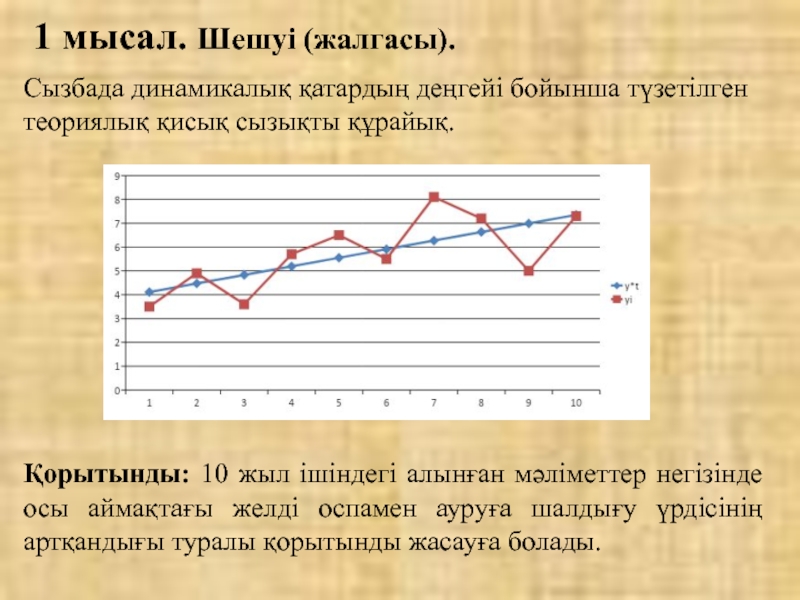
Слайд 24Cызбада динамикалық қатардың деңгейі бойынша түзетілген теориялық қисық сызықты құрайық.
Қорытынды: 10
жыл ішіндегі алынған мәліметтер негізінде осы аймақтағы желді оспамен ауруға шалдығу үрдісінің артқандығы туралы қорытынды жасауға болады.
1 мысал. Шешуі (жалгасы).
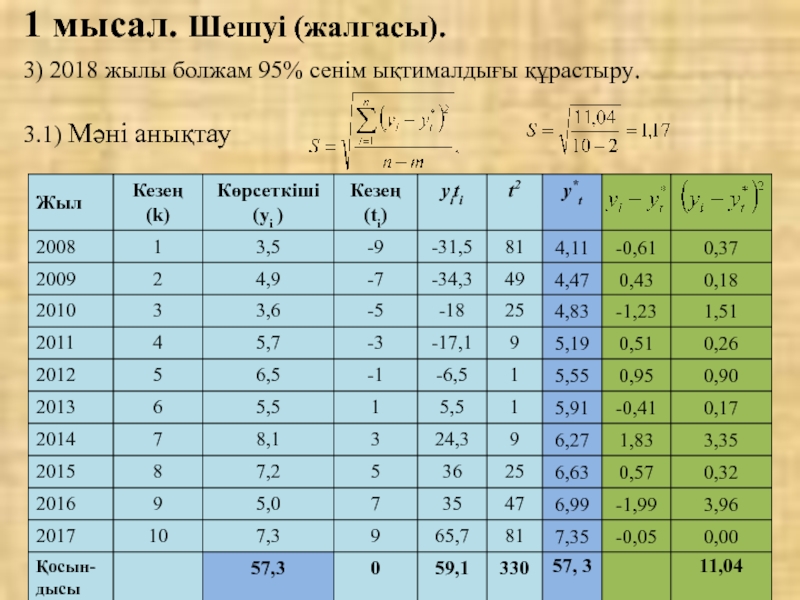
Слайд 253) 2018 жылы болжам 95% сенім ықтималдығы құрастыру.
3.1) Мәні анықтау
1 мысал. Шешуі (жалгасы).
Слайд 26t=11 уақытында динамикалық қатардың деңгейінің болжамған мәнінің нүктелік бағасын есептеу:
Кестеден сенімділік
коэффициенті табу: t (0,05; 8)= 2,31
Болжанатын аралықтын шекараларын формула бойынша анықтау:
Болжанатын аралықтын шекараларын формула бойынша анықтау:
Қорытынды: 95% ықтималдықпен, 2018 жылы осы аймақтығы желді оспамен науқастану 10000 мың адамға шаққанда 5,01-ден кем емес және 10,41 адамнан артық болады деп айтуға болады.
1 мысал. Шешуі (жалгасы).
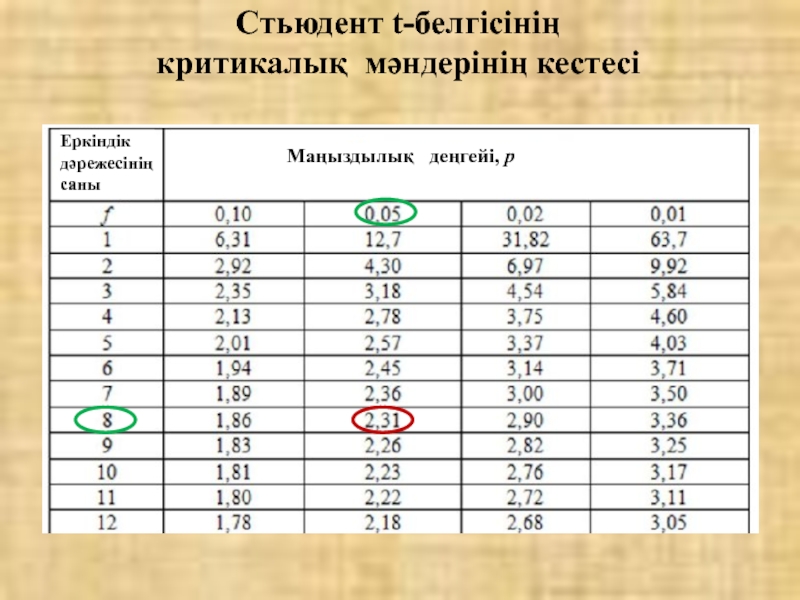
Слайд 27Стьюдент t-белгісінің
критикалық мәндерінің кестесі
Eркіндік дәрежесінің саны
Маңыздылық деңгейі, р
Слайд 28Дәріс жоспары:
Динамикалық қатардың түрлері.
Тренд түсінігі. Динамикалық қатарларды теңестіру әдістері.
Динамикалық қатарларды
болжау.
Динамикалық қатардың көрсеткіштері.
Динамикалық қатардың көрсеткіштері.
Слайд 29Динамикалық қатардың көрсеткіштері
Құбылыстың уақыт ішіндегі дамуының жылдамдығын және жітілігін талдау деңгейлерді
өзара салыстыру нәтижесінде алынатын статистикалық көрсеткіштер арқылы іске асады.
Слайд 30Мұндай көрсеткіштерге жататындар:
абсолюттік өсу;
өсудің шапшаңдығы;
бір пайыз өсудің абсолюттік
мәні және т.б.
Осы бойынша салыстыратын деңгейді есептік, ал салыстыру жүргізілетін деңгейді – базистік деп атау қабылданған.
Осы бойынша салыстыратын деңгейді есептік, ал салыстыру жүргізілетін деңгейді – базистік деп атау қабылданған.
Динамикалық қатардың көрсеткіштері
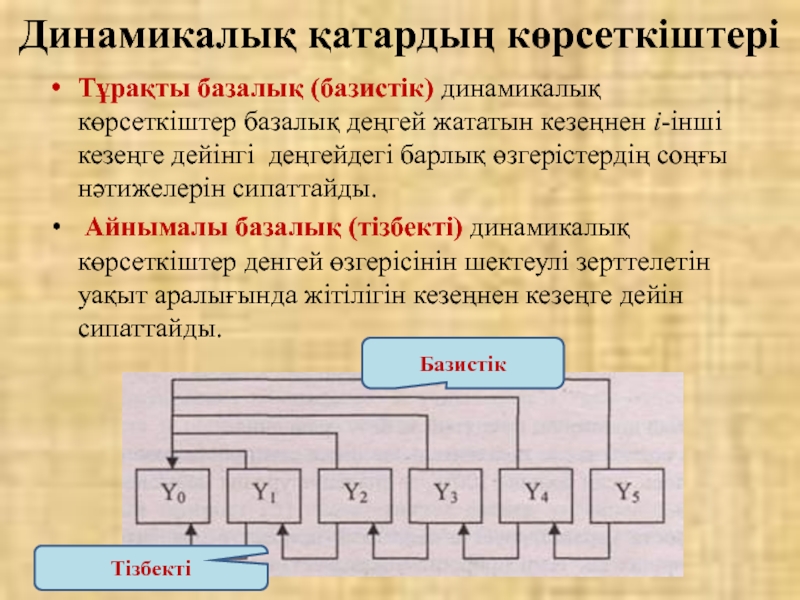
Слайд 31Тұрақты базалық (базистік) динамикалық көрсеткіштер базалық деңгей жататын кезеңнен i-інші кезеңге
дейінгі деңгейдегі барлық өзгерістердің соңғы нәтижелерін сипаттайды.
Айнымалы базалық (тізбекті) динамикалық көрсеткіштер денгей өзгерісінін шектеулі зерттелетін уақыт аралығында жітілігін кезеңнен кезеңге дейін сипаттайды.
Айнымалы базалық (тізбекті) динамикалық көрсеткіштер денгей өзгерісінін шектеулі зерттелетін уақыт аралығында жітілігін кезеңнен кезеңге дейін сипаттайды.
Базистік
Тізбекті
Динамикалық қатардың көрсеткіштері
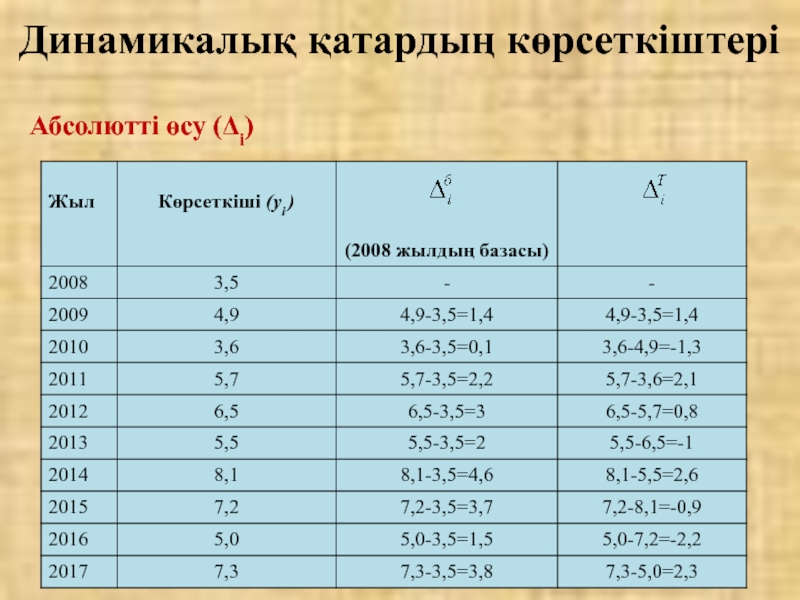
Слайд 32Абсолютті өсу (Δi) – динамикалық қатардың екі деңгейінің айырмашылығы ретінде анықталынатын
көрсеткіш. Ол қатардың берілген деңгейі салыстыру үшін база ретінде қабылданған деңгейден қаншалықты артық немесе кем екенін көрсетеді:
мұндағы - абсолюттік базистік өсу; уi – салыстырмалы кезеңнің деңгейі, у0 – базистік кезеңнің деңгейі.
Айнымалы базамен салыстырғанда абсолюттік өсу
тең болады,
мұндағы уi-1 – тікелей алдыңғы кезеңнің деңгейі.
мұндағы - абсолюттік базистік өсу; уi – салыстырмалы кезеңнің деңгейі, у0 – базистік кезеңнің деңгейі.
Айнымалы базамен салыстырғанда абсолюттік өсу
тең болады,
мұндағы уi-1 – тікелей алдыңғы кезеңнің деңгейі.
Динамикалық қатардың көрсеткіштері
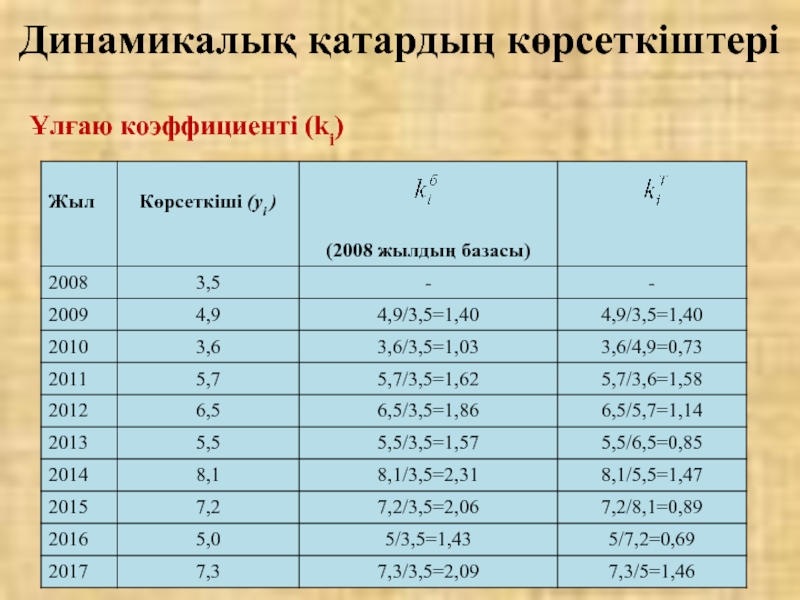
Слайд 34Ұлғаю коэффициенті (ki) екі салыстырмалы деңгейдің қатынасы ретінде анықталынады және берілген
деңгейдің қаншалықты базистік кезеңнің деңгейінен қанша рет артық екендігін көрсетеді :
базистік
тізбекті
базистік
тізбекті
Динамикалық қатардың көрсеткіштері
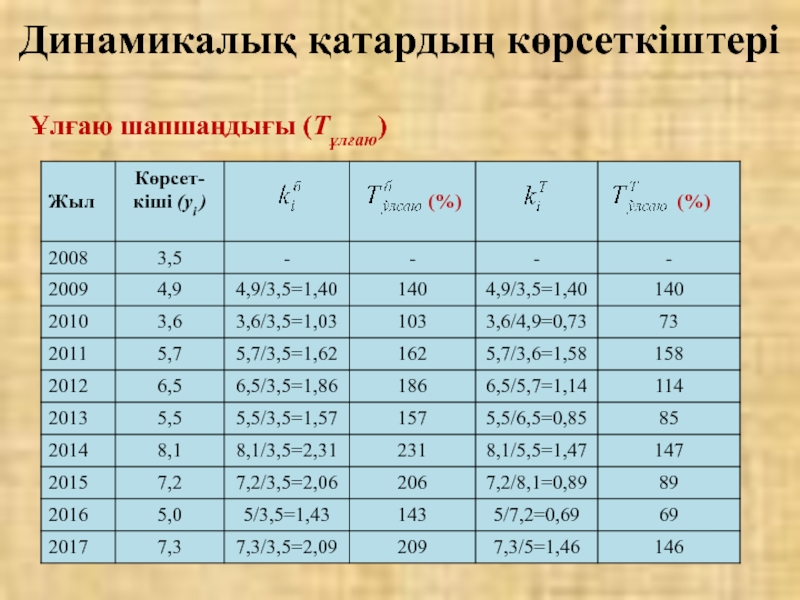
Слайд 36Егер өсудің коэффициенттері пайызбен өрнектелген болса, онда оларды ұлғаю шапшаңдығы деп
атайды, яғни олар көрсеткіштің пайызбен берілген жылдамдық өзгерісінің уақыт бірлігімен сипатталады:
Динамикалық қатардың көрсеткіштері
Слайд 38Өсу шапшаңдығы берілген кезең деңгейінің базистік деңгейден қанша пайызға көп (немесе
аз) екендігін көрсетеді. Бұл көрсеткіш екі түрде есептелінеді.
абсолютті өсудің базистік деңгейге қатынасы ретінде:
базистік ;
тізбекті
ұлғаюдың шапшаңдығы (%) және 100% арасындағы айырмашылық ретінде:
.
абсолютті өсудің базистік деңгейге қатынасы ретінде:
базистік ;
тізбекті
ұлғаюдың шапшаңдығы (%) және 100% арасындағы айырмашылық ретінде:
.
Динамикалық қатардың көрсеткіштері
Слайд 40Өсудің бір пайыздық абсолюттік мәні (Аi) алынған өсудің шапшаңдығының мәнін дұрыс
бағалау үшін пайдаланылады.
Тек тізбекті әдіспен есептеуге болады.
Тек тізбекті әдіспен есептеуге болады.
Динамикалық қатардың көрсеткіштері
Слайд 42Зерттелетін құбылыстың динамикасын жалпы сипаттауда кезең қатары үшін түрлі орташа көрсеткішті
анықтайды.
Орташа абсолюттік өсу – уақыт аралығындағы көрсеткіштің орташа шамасының өзгеруі.
Орташа абсолюттік өсу – уақыт аралығындағы көрсеткіштің орташа шамасының өзгеруі.
Динамикалық қатардың көрсеткіштері
Слайд 43Ұлғаюдың орташа шапшаңдығы – бұл динамикалық қатар деңгейілері жітілігінің өзгеруі сипаттамасы.
Ол бірлік уақыт ішінде динамикалық қатар деңгейінің орташа қанша рет өзгеретіндігін көрсетеді:
,
мұндағы - ұлғаюдың орташа коэффициенті;
n - қатар деңгейінің саны.
,
мұндағы - ұлғаюдың орташа коэффициенті;
n - қатар деңгейінің саны.
Динамикалық қатардың көрсеткіштері
Слайд 45Бақылау сұрақтары:
Динамикалық қатар дегеніміз не? Ол қандай элементтерден тұрады?
Қандай динамикалық қатарларды
білесіздер?
Тренд дегеніміз не?
Динамикалық қатар қандай жолымен түзетіледі?
Сызықты трендтің коэффициентері қалай анықталады?
Базистік және тізбекті көрсеткіштерін арасында қандай айырмашылық бар?
Қандай салыстырмалы динамикалық көрсеткіштерді білесіздер?
Қандай орташа динамикалық көрсеткіштерді білесіздер?
Тренд дегеніміз не?
Динамикалық қатар қандай жолымен түзетіледі?
Сызықты трендтің коэффициентері қалай анықталады?
Базистік және тізбекті көрсеткіштерін арасында қандай айырмашылық бар?
Қандай салыстырмалы динамикалық көрсеткіштерді білесіздер?
Қандай орташа динамикалық көрсеткіштерді білесіздер?
