на
приращения соответствующих
независимых переменных.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциалом функции нескольких переменных презентация
Содержание
Слайд 116.4. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
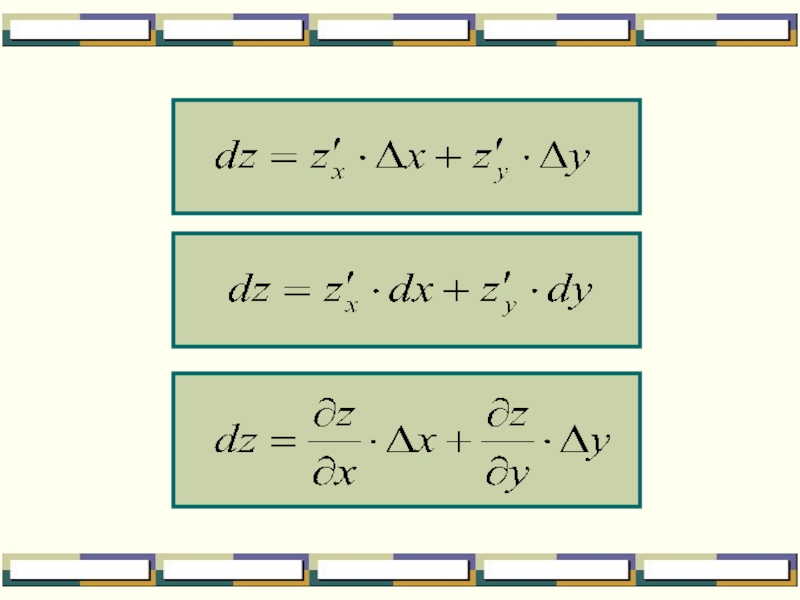
Дифференциалом функции называется
сумма произведений частных
производных этой функции
Слайд 3Функция z=f(x,y) называется
дифференцируемой в точке (x,y), если
ее полное приращение можно
представить
в виде:
Слайд 4Где dz – дифференциал функции;
- бесконечно малые величины при
Таким образом,
дифференциал функции нескольких переменных – это главная, линейная относительно приращений Δх и Δу часть полного приращения функции.
Слайд 5Для функции одной переменной y=f(x) существование конечной производной
и представление приращения
функции в виде
являются равнозначными утверждениями.
Для функции нескольких переменных существование частных производных является необходимым но не достаточным условием дифференцируемости функции.
Слайд 6ТЕОРЕМА.
Если частные производные функции
z=f(x,y) существуют в некоторой
окрестности точки (x,y) и непрерывны
в
самой точке (x,y), то функция
z=f(x,y) дифференцируема в этой точке.
z=f(x,y) дифференцируема в этой точке.