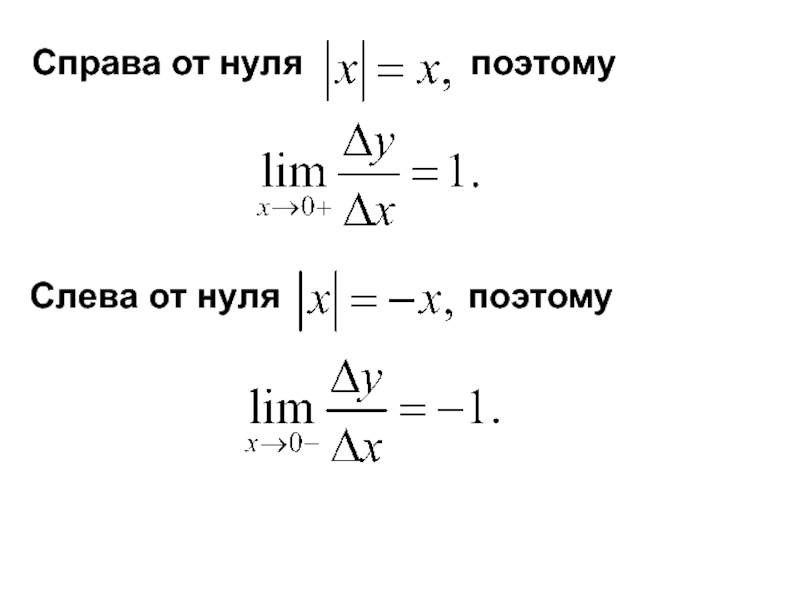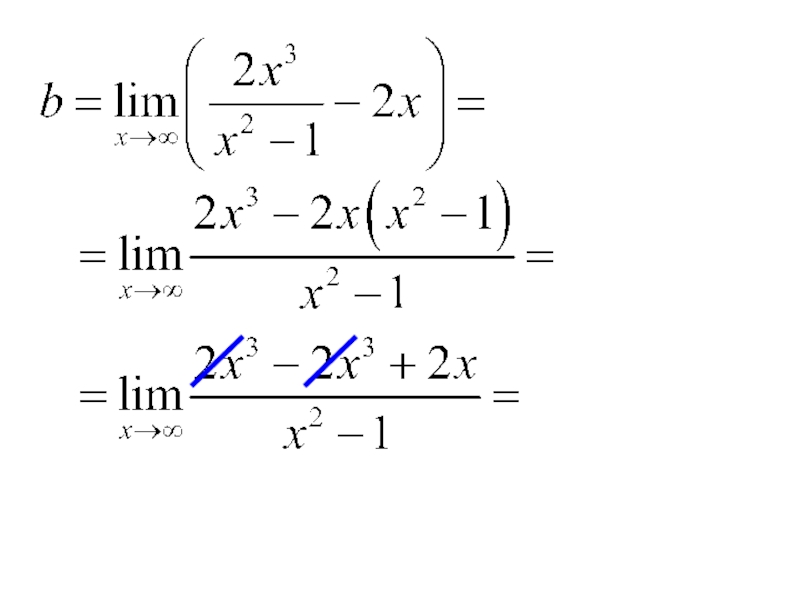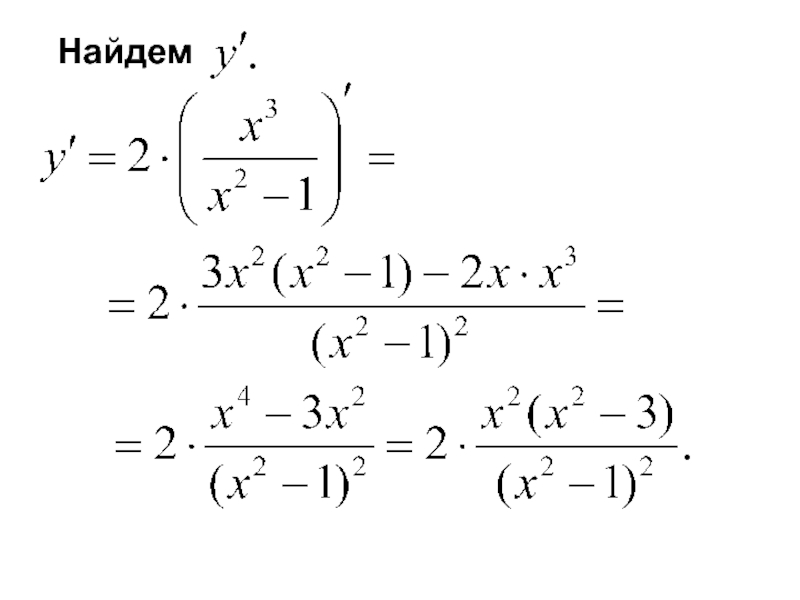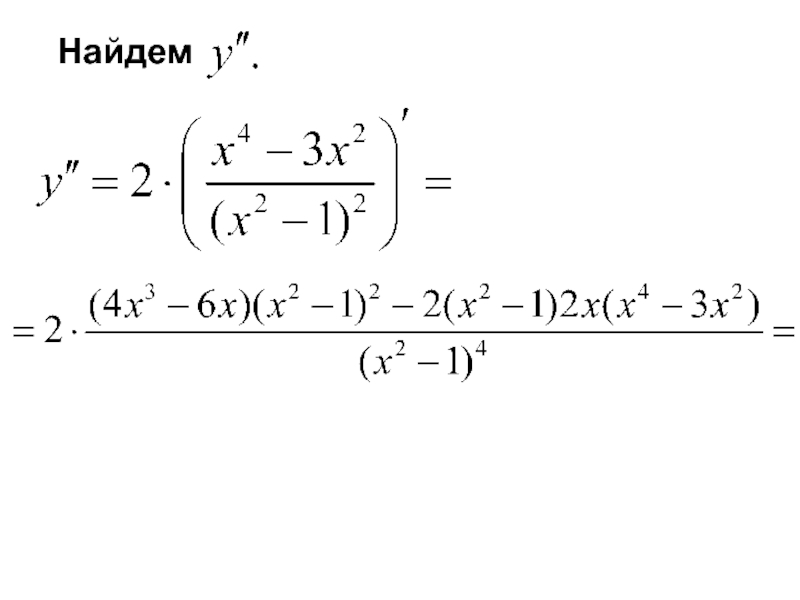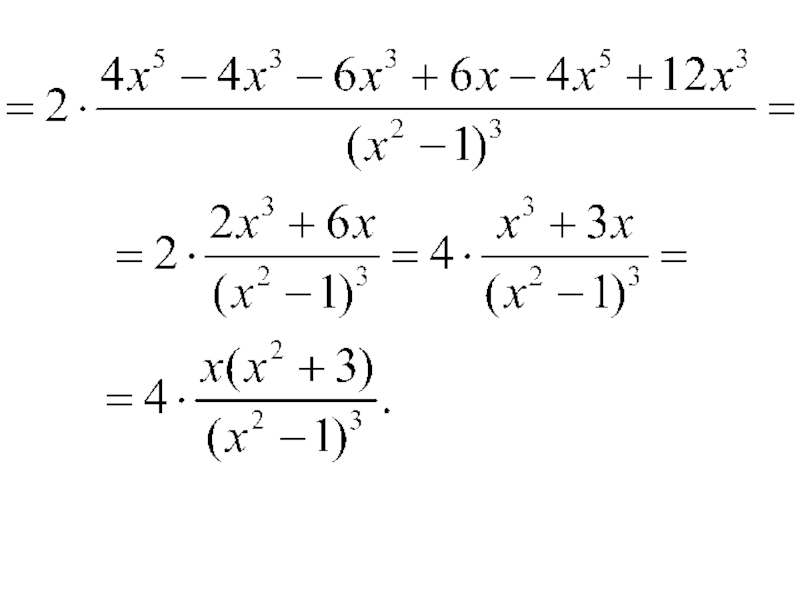помощью производной
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциал функции. Исследование функции с помощью производной презентация
Содержание
- 1. Дифференциал функции. Исследование функции с помощью производной
- 2. Рассмотрим функцию Найдем Дифференциал функции
- 3. Приращение функции можно рассматривать как сумму двух слагаемых: - линейное относительно - нелинейное относительно
- 4. При
- 5. Теорема. Если функция
- 6. Примеры. Найти дифференциалы функций 1) 2)
- 7. Теорема. Если функция
- 8. Пример. В точке
- 9. Справа от нуля
- 10. Таким образом, отношение
- 11. Схема исследования функции 1) Найти область определения
- 12. 4) Найти асимптоты кривой 5) Исследовать функцию
- 13. 6) Исследовать функцию по знаку второй производной
- 14. Пример. Исследовать функцию и построить график: 1) Область определения:
- 15. 2) Чётность, нечётность. четная, если нечетная, если
- 16. 3) Точки пересечения с осями координат 4)
- 17. Асимптоты бывают: a) вертикальные. Они параллельны оси Уравнение вертикальной асимптоты b) наклонные. Уравнение где
- 18. c) если
- 19. Аналогично, - вертикальная асимптота. Заметим, что кривая
- 20. Найдем наклонную асимптоту
- 22. - наклонная асимптота.
- 23. Найдем
- 24. - точка максимума. - точка минимума. + - + -
- 25. Можно было не рассматривать
- 26. Найдем
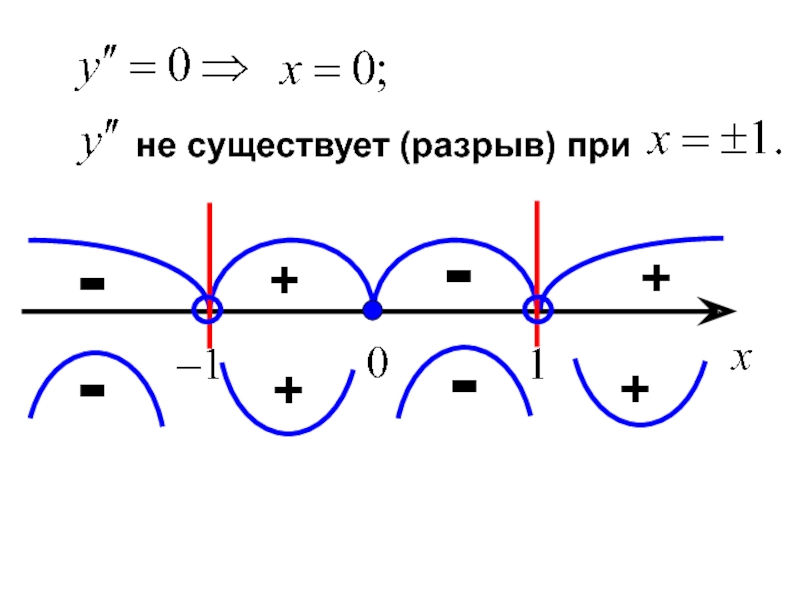
- 28. не существует (разрыв) при + - + -
- 29. Если
- 30. Точки, в которых выпуклость меняется на вогнутость
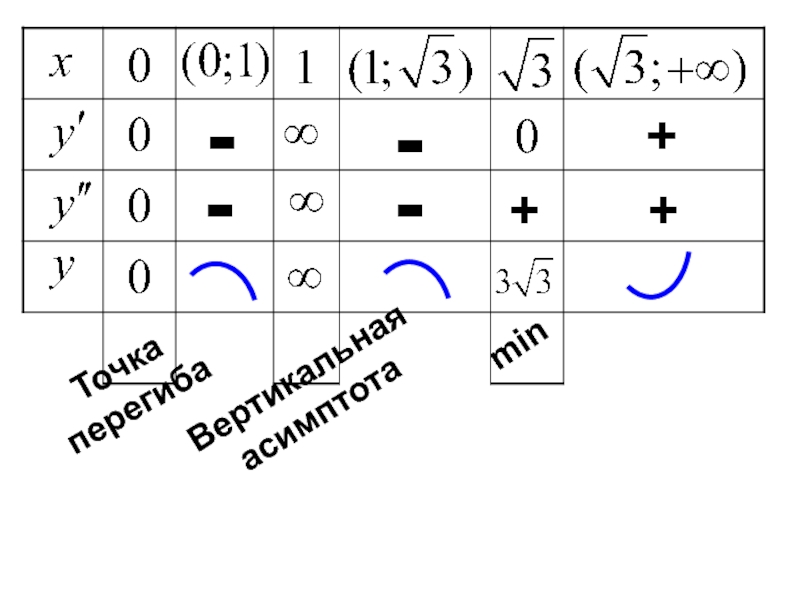
- 31. + - - - - + + Точка перегиба Вертикальная асимптота min
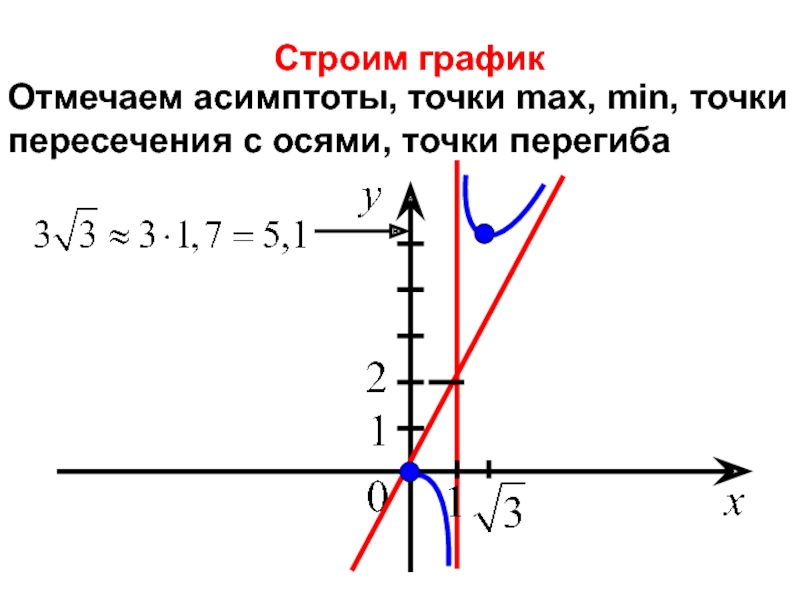
- 32. Строим график Отмечаем асимптоты, точки max,
- 33. Для строим график, используя нечетность функции.
Рассмотрим функцию Найдем Дифференциал функции
Слайд 1Лекция N12
Лектор: доц. Лаптева Надежда Александровна
Тема: Дифференциал функции. Исследование функции
с
Слайд 3Приращение функции можно рассматривать как сумму двух слагаемых:
- линейное относительно
-
нелинейное относительно
Слайд 4При оба слагаемых
стремятся к нулю, но второе слагаемое быстрее стремится к нулю. Поэтому при малых считают, что (т.е. считают, что приближенно равно линейной части). Эту часть называют главной частью приращения функции или дифференциалом.
Дифференциал функции обозначают
Слайд 5Теорема. Если функция
имеет в точке дифференциал, то она имеет в этой точке производную и наоборот, если функция имеет в точке производную, то она имеет в этой точке дифференциал.
Выражение для дифференциала записывается в форме
Слайд 7Теорема. Если функция дифференцируема в
точке то она в этой точке непрерывна.
Связь между дифференцируемостью и непрерывностью функции
Обратная теорема неверна: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми.
Слайд 10Таким образом, отношение при справа и
слева имеет различные пределы, а это значит, что при это отношение предела не имеет, т.е. производная в точке
не существует.
Слайд 11Схема исследования функции
1) Найти область определения функции
2) Исследовать функцию на четность
и нечетность
3) Найти точки пересечения с осями координат
Слайд 124) Найти асимптоты кривой
5) Исследовать функцию по знаку первой производной
, т.е. найти интервалы возрастания, убывания, точки экстремума
Слайд 136) Исследовать функцию по знаку второй производной ,
т.е. найти интервалы выпуклости, вогнутости, точки перегиба
7) Построить график. Для построения графика можно все результаты исследования свести в таблицу.
Слайд 152) Чётность, нечётность.
четная, если
нечетная, если
функция нечетная, следовательно график функции симметричен относительно
начала координат.
Слайд 163) Точки пересечения с осями координат
4) Асимптоты – это прямые, к
которым стремится график функции при неограниченном удалении от начала координат.
Слайд 17Асимптоты бывают:
a) вертикальные. Они параллельны оси
Уравнение вертикальной асимптоты
b) наклонные. Уравнение
где
Слайд 18c) если то
и наклонная асимптота становится горизонтальной, т.е. параллельной оси
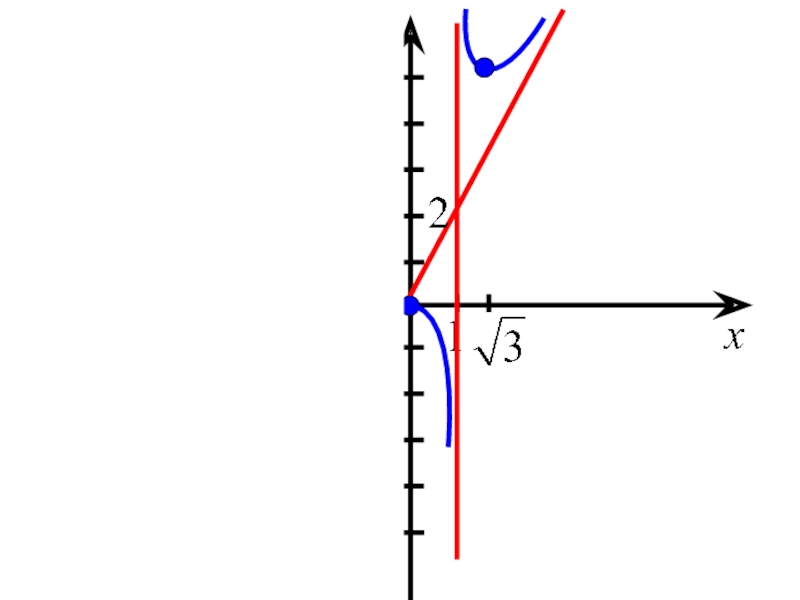
Найдем асимптоты кривой
Т.к.
то - вертикальная асимптота.
Слайд 19Аналогично,
- вертикальная асимптота.
Заметим, что кривая может иметь сколько угодно вертикальных асимптот.
Пример.
Вертикальные асимптоты
где
Слайд 25Можно было не рассматривать т.е.
функция нечетная и достаточно построить график только для а затем отобразить график симметрично относительно начала координат.
Слайд 30Точки, в которых выпуклость меняется на вогнутость или наоборот, называются точками
перегиба.
7) Для построения графика сделаем сводную таблицу. Т.к. функция нечетная, то будем рассматривать только
- точка перегиба.
