- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дискретная математика. Отношения презентация
Содержание
- 1. Дискретная математика. Отношения
- 2. Унарные отношения Отношения – один из способов
- 3. Бинарные (двухместные отношения) используются для определения каких-либо
- 4. n-местное отношение
- 5. Бинарные отношения Пример. Пусть
- 6. Область определения и область значений Область определения
- 7. Пример. Для отношения рассмотренного в предыдущем
- 8. Способы задания отношений 2. Характеристическим свойством. Например,
- 9. Способы задания отношений
- 10. Пример. R ={(1,5), (2,4), (3,6), (6,2)} на
- 11. Способы задания отношений
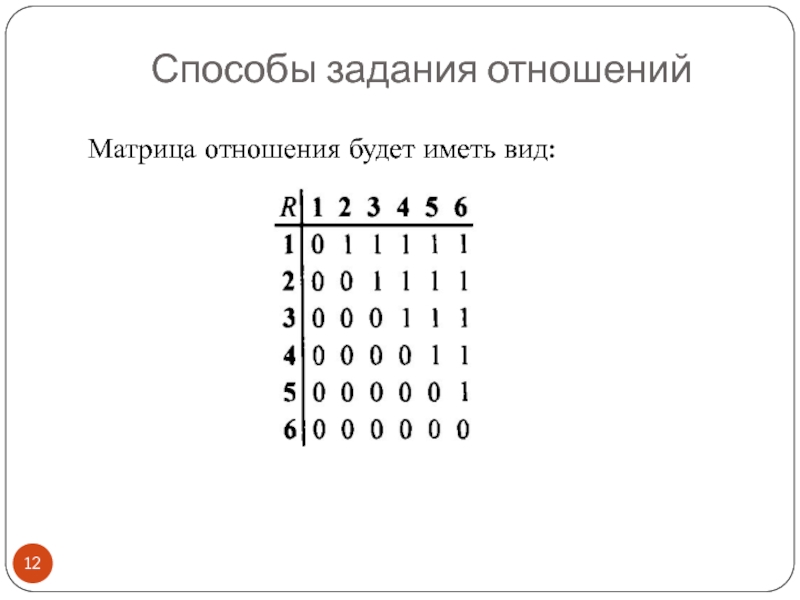
- 12. Матрица отношения будет иметь вид: Способы задания отношений
- 13. Способы задания отношений
- 14. Способы задания отношений
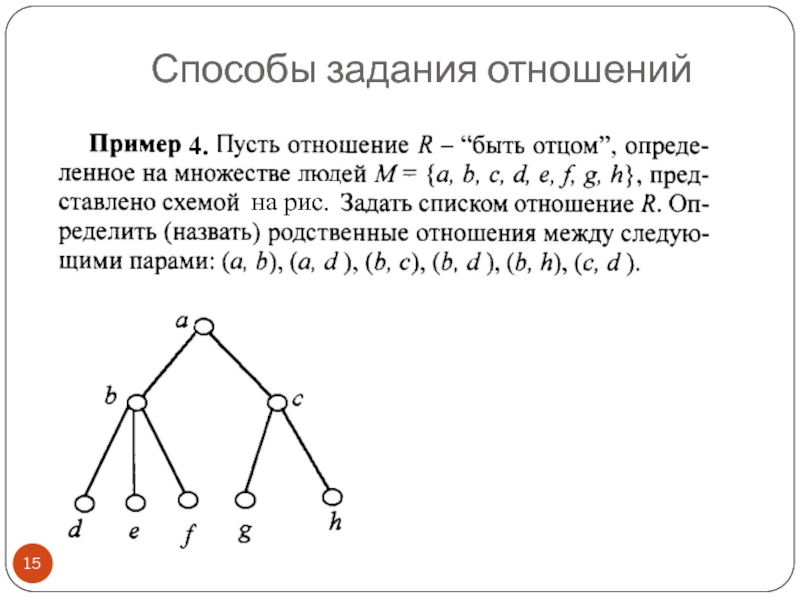
- 15. Способы задания отношений 4. на рис.
- 16. Рассмотрим подробнее графический способ задания отношений. Графические
- 17. Координатный метод Способы задания отношений Пусть дано
- 18. Линейно-координатный метод Способы задания отношений Представим то
- 19. Линейный метод Используя параллельные вертикальные линии для
- 20. Графовый метод Элементы множества, на котором строится
- 21. Задача. По матрице представить отношение списком, графически Способы задания отношений
- 22. Свойства отношений
- 23. Свойства отношений
- 24. Пример. Пусть Определено на множестве Зададим списком:
- 25. Свойства отношений
- 26. Пример. На булеане множества М={1, 2, 3}
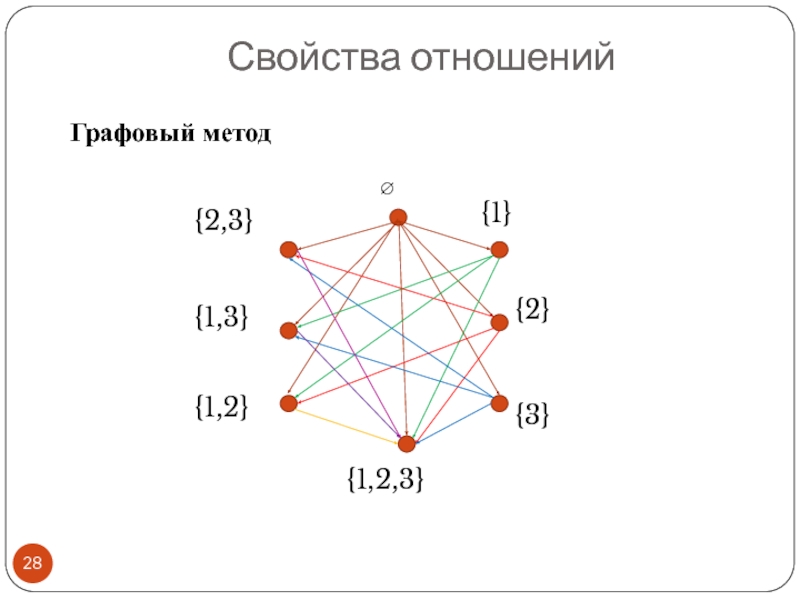
- 27. Свойства отношений ∅ ∅ {1} {2} {3}
- 28. Свойства отношений ∅
- 29. Свойства отношения R – «быть собственным подмножеством»:
- 30. Пример. R Задать всеми способами и определить
- 31. Матрица отношения «иметь общий делитель» Свойства отношений
- 32. Свойства отношения R- «иметь общий делитель»:
- 33. Свойства отношений
- 34. Свойства отношений Матрица рефлексивного отношения имеет на
- 35. Свойства отношений На диаграмме графового представления
- 36. Свойства отношений
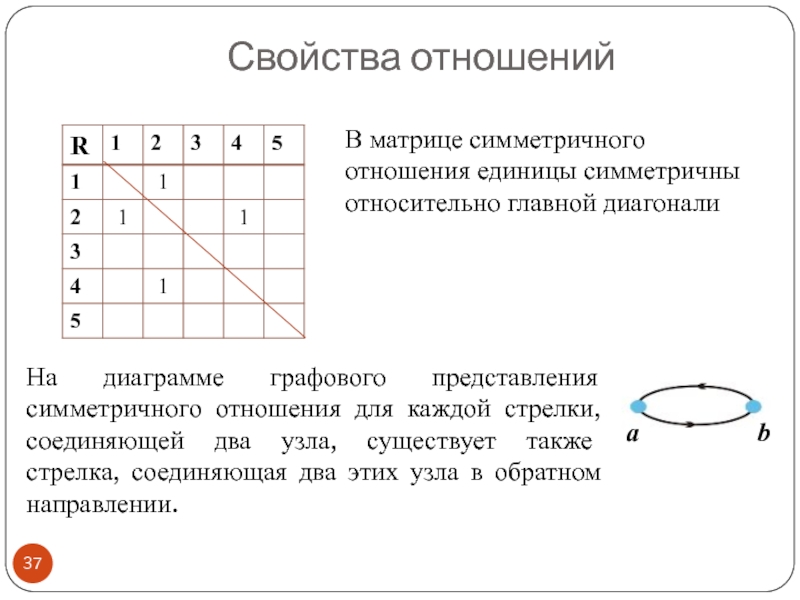
- 37. Свойства отношений В матрице симметричного отношения единицы
- 38. Свойства отношений Пример матрицы антисимметричного отношения
- 39. На диаграмме графового представления антисимметричного отношения ни
- 40. 5) На диаграмме графового представления транзитивного отношения
- 41. Отношения эквивалентности и порядка Пример. На рисунке
- 42. Определение: Отношение эквивалентности– это бинарное отношение на
- 43. Отношение эквивалентности Пример. R- «быть равным» на
- 44. Примеры отношений эквивалентности: Отношение «быть равным»,
- 45. Отношение толерантности Определение: Отношением толерантности (или просто
- 46. Отношения «быть другом», «быть знакомым», -
- 47. Отношение строгого порядка Определение: Отношение строгого порядка–
- 48. Отношение нестрогого порядка Определение: Отношение нестрогого порядка–
- 49. Отношения порядка Множество
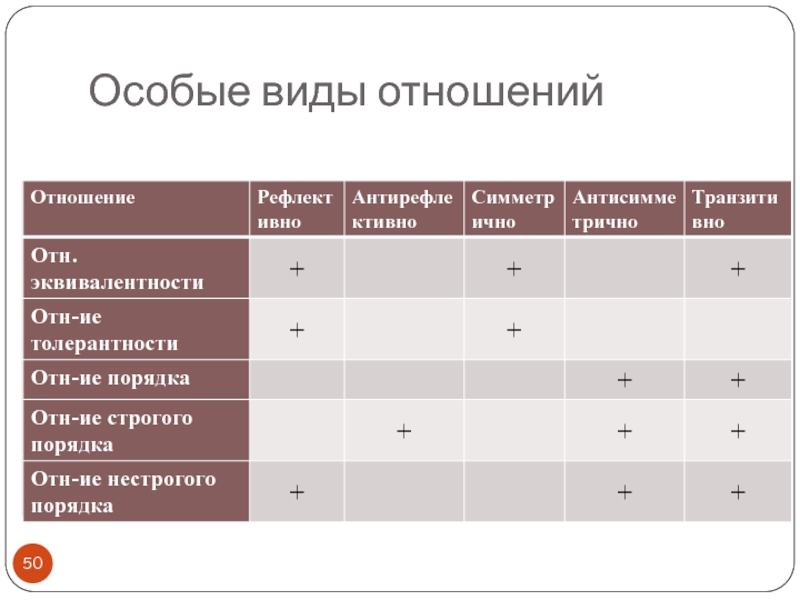
- 50. Особые виды отношений
- 51. Задача 2. Дан граф некоторого отношения. Дополните
- 52. Задача 3. Назовем два слова сходными, если
Слайд 2Унарные отношения
Отношения – один из способов задания взаимосвязей между элементами множества.
Унарные
Пример.
М – множество студентов гр.08АСУ;
R – «быть светловолосым»
R={Гуничев, Хомутинникова, Смирнов, Федотова, Баранов}
Унарным отношением R на множестве М называется подмножество R множества М, состоящее из элементов множества М, обладающих свойством R, т.е. а ∈R и R⊆М.
Слайд 3Бинарные (двухместные отношения) используются для определения каких-либо взаимосвязей, которыми характеризуются пары
Например, М-множество людей,
отношение R- «жить в одном городе»,
R = {(Иванов, Сидоров), (Смит, Джонсон), …}
Все пары (a,b) элементов из М, между которыми имеет место отношение R, образуют подмножество пар из множества всех возможных пар элементов М × М = М2, называемое бинарным отношением R, т.е. (a,b)∈R, при этом R⊆ М × М.
Бинарные отношения
Если а и b находятся в отношении R, то это часто записывают как а R b.
Слайд 5Бинарные отношения
Пример. Пусть
Т.е. }. Перечислим все такие пары:
Т.о. мы задали отношение R⊆ A × A
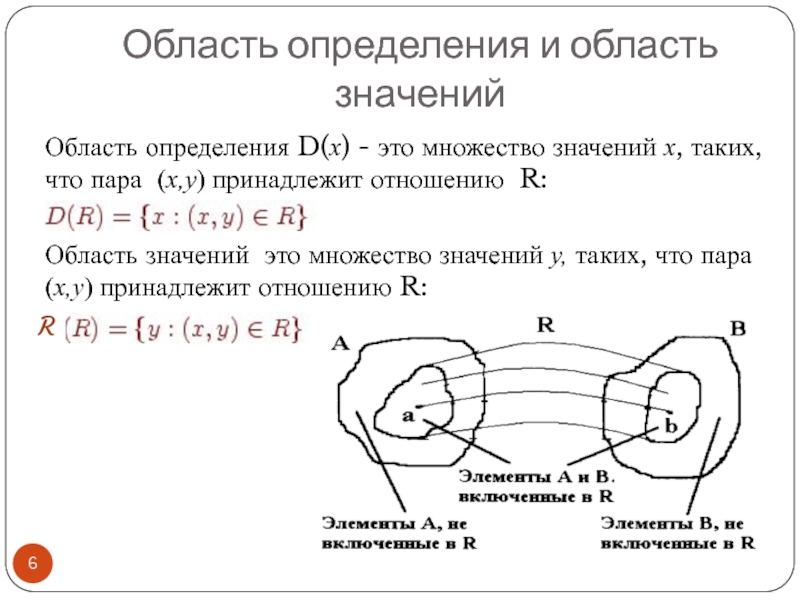
Слайд 6Область определения и область значений
Область определения D(x) - это множество значений
Область значений это множество значений y, таких, что пара (x,y) принадлежит отношению R:
R
Слайд 7Пример. Для отношения
рассмотренного в предыдущем примере, область определения и область значений
Область определения и область значений
R
Слайд 8Способы задания отношений
2. Характеристическим свойством.
Например,
3. Графически.
Например, R ={(1,5), (2,4), (3,6),
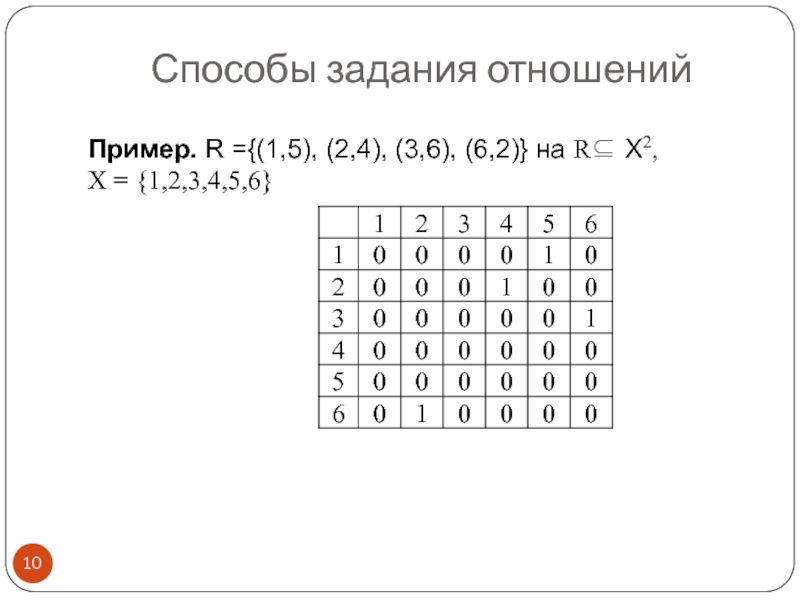
Слайд 10Пример. R ={(1,5), (2,4), (3,6), (6,2)} на R⊆ Х2,
Х =
Способы задания отношений
Слайд 16Рассмотрим подробнее графический способ задания отношений.
Графические методы задания отношения:
Координатный метод;
Линейно-координатный метод;
Линейный
Графовый метод.
Способы задания отношений
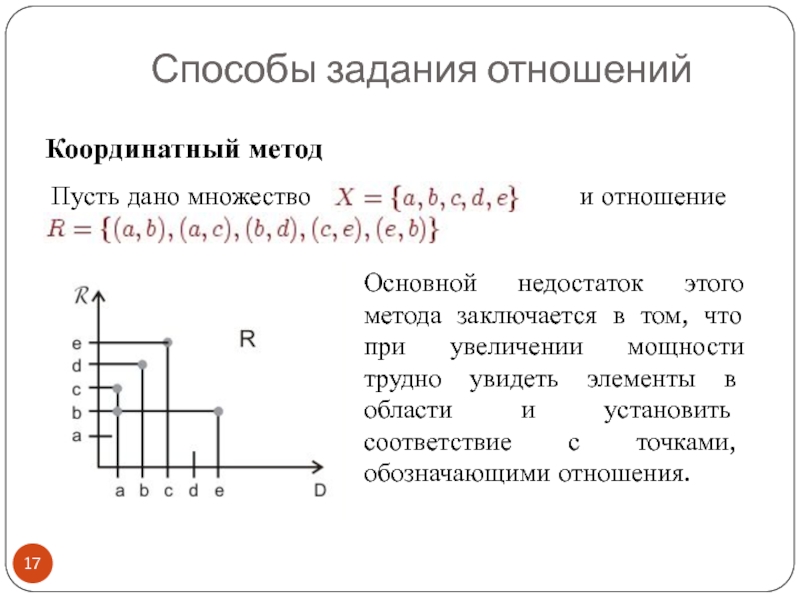
Слайд 17Координатный метод
Способы задания отношений
Пусть дано множество
Основной недостаток этого метода заключается в том, что при увеличении мощности трудно увидеть элементы в области и установить соответствие с точками, обозначающими отношения.
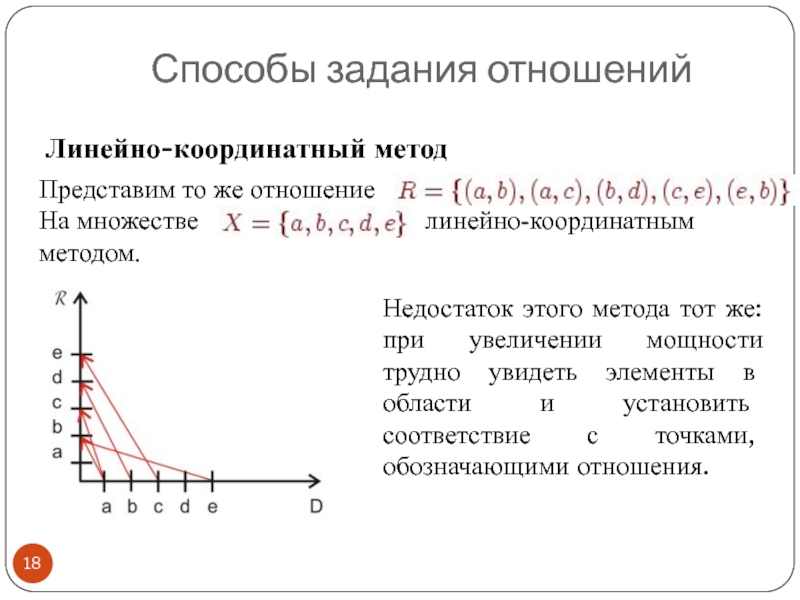
Слайд 18Линейно-координатный метод
Способы задания отношений
Представим то же отношение
На множестве
Недостаток этого метода тот же: при увеличении мощности трудно увидеть элементы в области и установить соответствие с точками, обозначающими отношения.
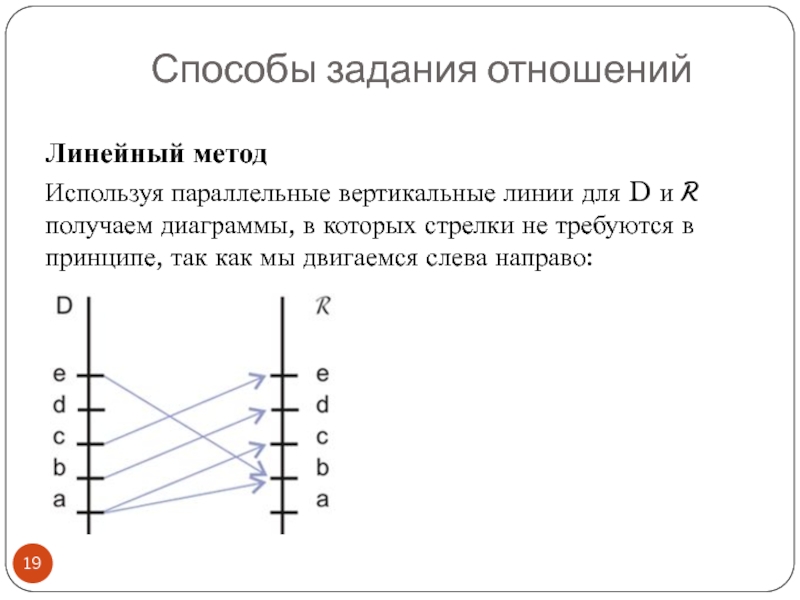
Слайд 19Линейный метод
Используя параллельные вертикальные линии для D и R получаем диаграммы,
Способы задания отношений
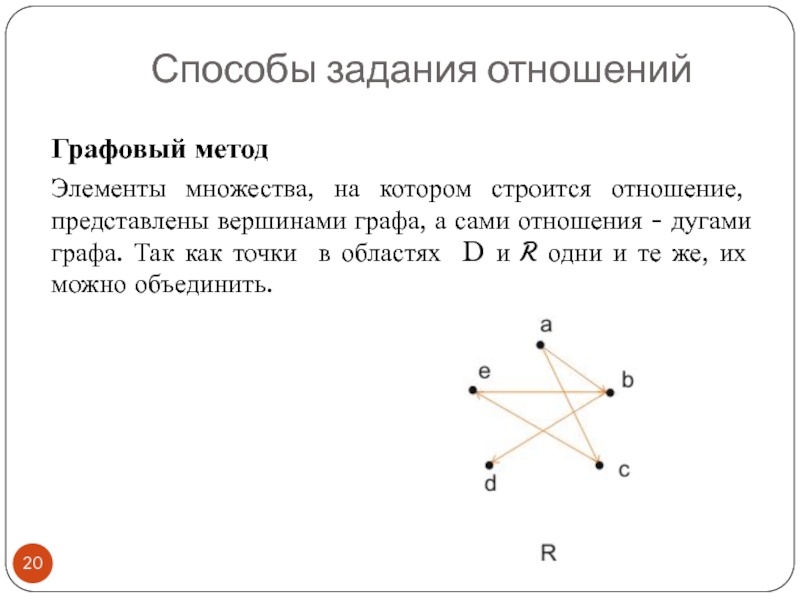
Слайд 20Графовый метод
Элементы множества, на котором строится отношение, представлены вершинами графа, а
Способы задания отношений
Слайд 24Пример. Пусть
Определено на множестве
Зададим списком:
Свойства отношения R:
рефлексивно, так как х/х=1
несимметрично, поскольку, например, 2 - делитель 4, а 4 не является делителем 2;
антисимметрично, так как если x/y ∈R и y/x ∈R, то х=у.
транзитивно, так как (2, 4) и (4, 8) влечет (2, 8);
Свойства отношений
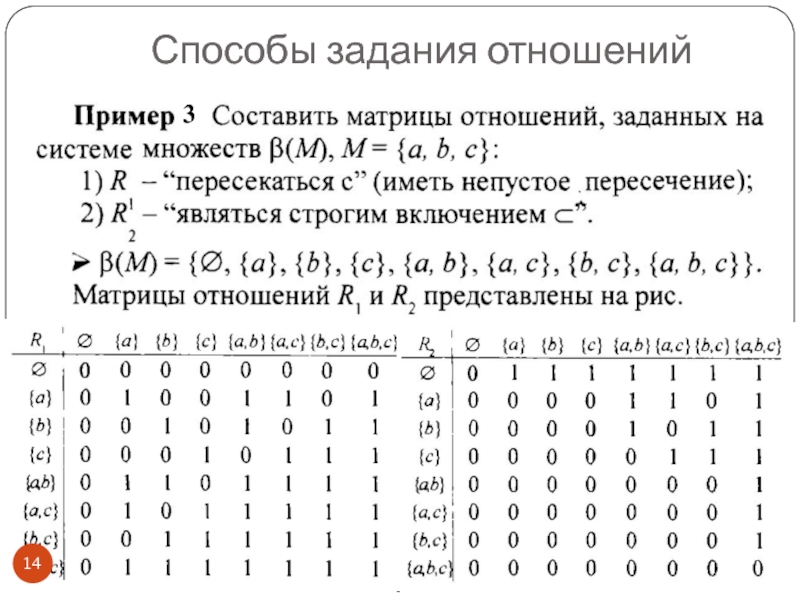
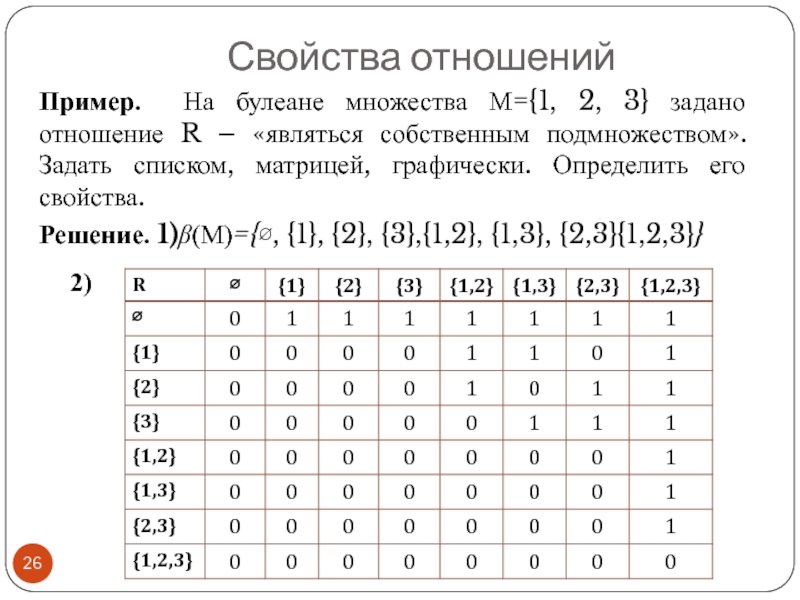
Слайд 26Пример. На булеане множества М={1, 2, 3} задано отношение R –
Решение. 1)β(М)={∅, {1}, {2}, {3},{1,2}, {1,3}, {2,3}{1,2,3}}
Свойства отношений
2)
Слайд 27Свойства отношений
∅
∅
{1}
{2}
{3}
{1,2}
{1,3}
{2,3}
{1,2,3}
{1}
{3}
{2}
{1,2}
{1,3}
{2,3}
{1,2,3}
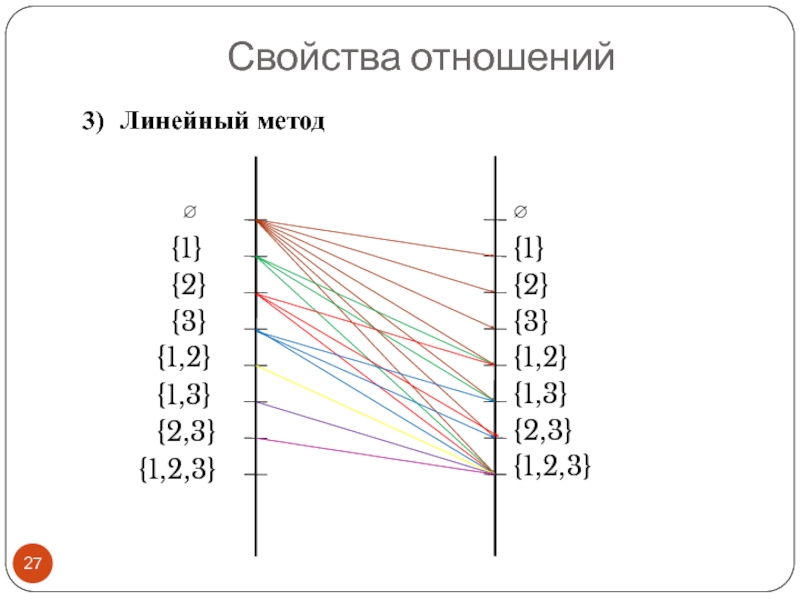
3)
Линейный метод
Слайд 29Свойства отношения R – «быть собственным подмножеством»:
Не является рефлексивным
Антирефлексивно, так как
Не является симметричным, так как, например, {1}⊂{1,2}, но {1,2}⊄{1}
антисимметрично, так как для любых множеств А и В из того, что А⊂В и В⊂А следует А=В.
Является транзитивным, так как, если А⊂В и В⊂С, то А⊂С
Свойства отношений
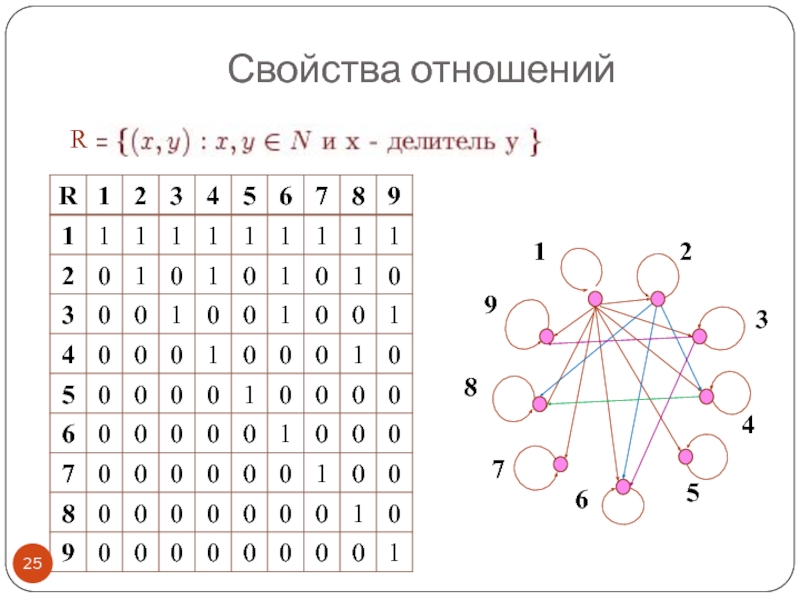
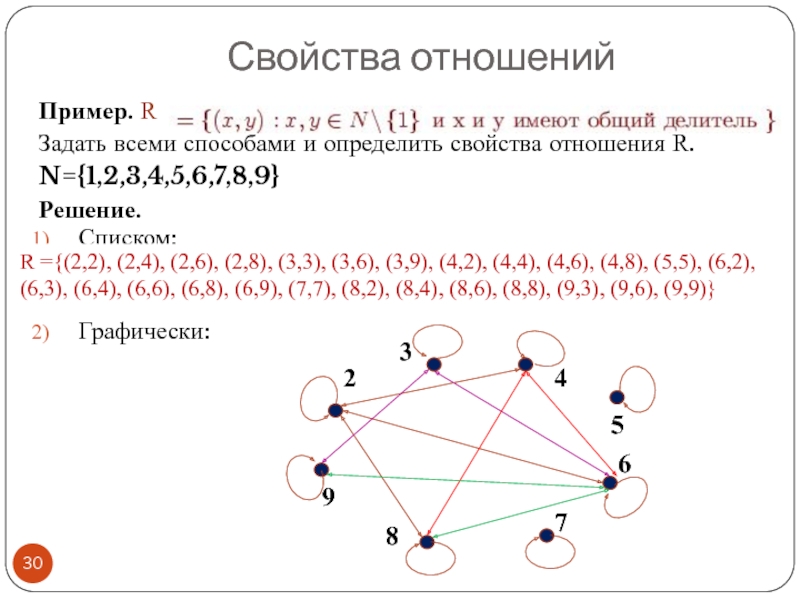
Слайд 30Пример. R
Задать всеми способами и определить свойства отношения R.
N={1,2,3,4,5,6,7,8,9}
Решение.
Списком:
Графически:
Свойства отношений
R
4
9
5
7
6
8
3
2
Слайд 32Свойства отношения R- «иметь общий делитель»:
рефлексивно, так как выполняется аRа
Не антирефлексивно;
симметрично, так как если пара (а, b) имеет общий делитель, то и пара (b, а) тоже имеет общий делитель;
не антисимметрично;
не транзитивно, так как, например, 2 и 6 имеют общий делитель, 6 и 9 имеют общий делитель, но 2 и 9 не имеют общий делитель, т.е.
(2,6)∈R, (6,9)∈R ⇒(2,9)∈R .
Свойства отношений
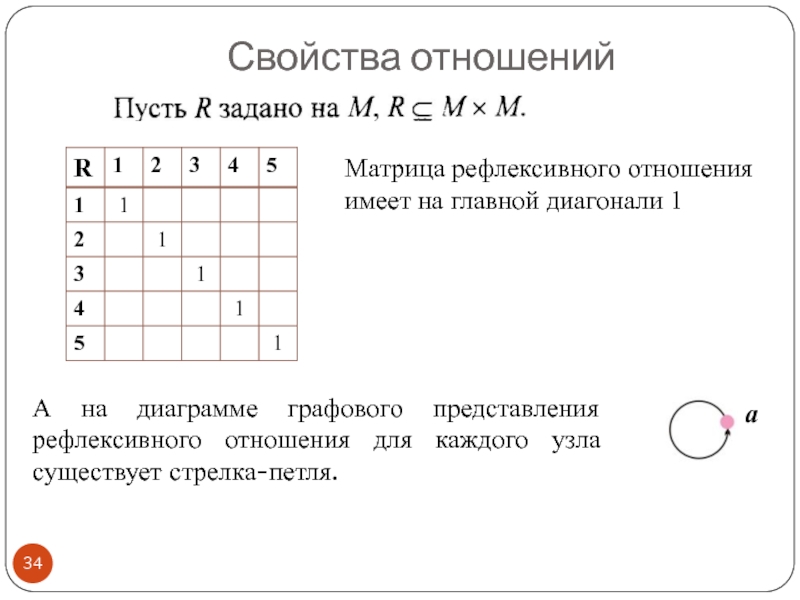
Слайд 34Свойства отношений
Матрица рефлексивного отношения имеет на главной диагонали 1
А на диаграмме
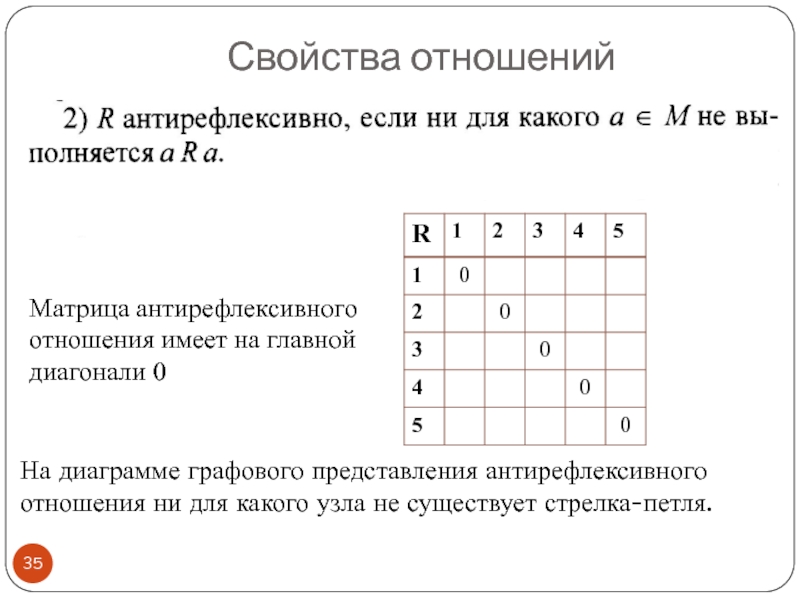
Слайд 35Свойства отношений
На диаграмме графового представления антирефлексивного отношения ни для какого узла
Матрица антирефлексивного отношения имеет на главной диагонали 0
Слайд 37Свойства отношений
В матрице симметричного отношения единицы симметричны относительно главной диагонали
На диаграмме
a
b
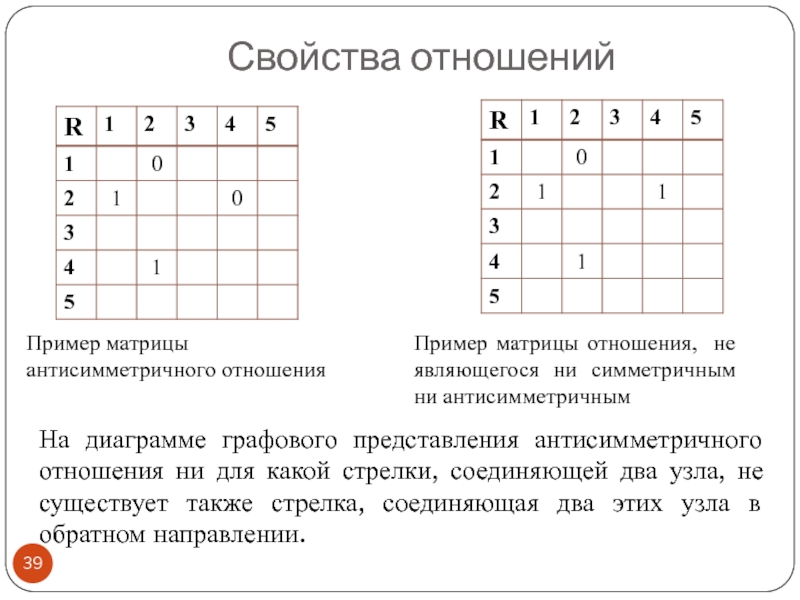
Слайд 39На диаграмме графового представления антисимметричного отношения ни для какой стрелки, соединяющей
Свойства отношений
Пример матрицы антисимметричного отношения
Пример матрицы отношения, не являющегося ни симметричным ни антисимметричным
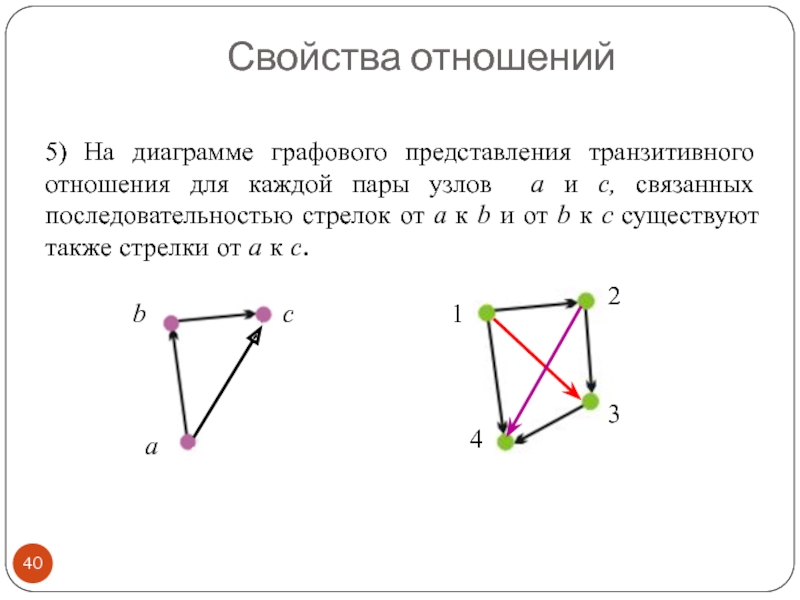
Слайд 405) На диаграмме графового представления транзитивного отношения для каждой пары узлов
1
2
3
4
Свойства отношений
c
a
b
Слайд 41Отношения эквивалентности и порядка
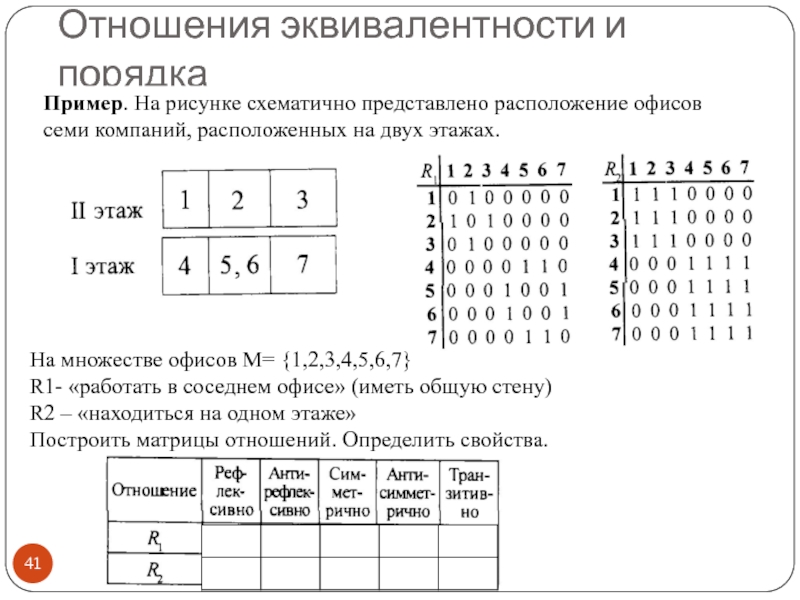
Пример. На рисунке схематично представлено расположение офисов семи
На множестве офисов М= {1,2,3,4,5,6,7}
R1- «работать в соседнем офисе» (иметь общую стену)
R2 – «находиться на одном этаже»
Построить матрицы отношений. Определить свойства.
Слайд 42Определение: Отношение эквивалентности– это бинарное отношение на множестве Х, удовлетворяющее следующим
Рефлексивность (xRx)
Симметричность (xRy & yRx)
Транзитивность (xRy & yRz → xRz)
Отношение эквивалентности
Слайд 43Отношение эквивалентности
Пример. R- «быть равным» на множестве натуральных чисел.
Свойства:
Рефлексивно, т.к. а=а,
Симметрично, т.к. если а=b, то и b=а, ∀а, b∈N;
Транзитивно, т.к. если а=b и b=с, то и а=с, ∀а, b, с∈N.
Т.к. отношение R- «быть равным» на множестве натуральных чисел рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
Слайд 44 Примеры отношений эквивалентности:
Отношение «быть равным», «иметь один и тот же
рефлексивность
симметричность
транзитивность
Отношение эквивалентности
Отношение эквивалентности
Слайд 45Отношение толерантности
Определение: Отношением толерантности (или просто толерантностью) на множестве X называется
Отношение эквивалентности – частный случай отношения толерантности.
Слайд 46Отношения «быть другом», «быть знакомым», - отношения толерантности, так как
Отношение «иметь непустое пересечение» для множеств – отношение толерантности.
Отношение толерантности
рефлексивность
симметричность
Отношение толерантности
Слайд 47Отношение строгого порядка
Определение: Отношение строгого порядка– это бинарное отношение на множестве
Антирефлексивность (xRx)
Антисимметричность (xRy → yRx)
Транзитивность (xRy & yRz → xRz)
Слайд 48Отношение нестрогого порядка
Определение: Отношение нестрогого порядка– это бинарное отношение на множестве
Рефлексивность (xRx)
Антисимметричность (xRy → yRx)
Транзитивность (xRy & yRz → xRz)
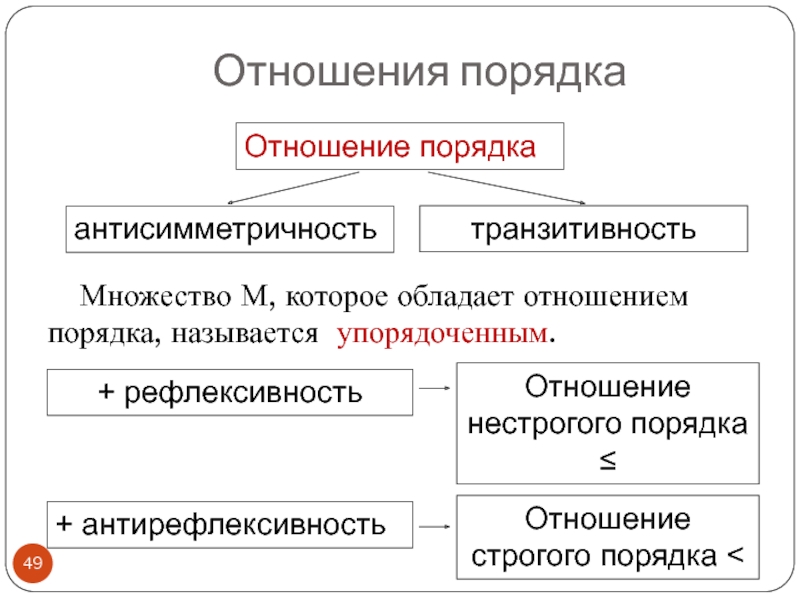
Слайд 49Отношения порядка
Множество М, которое обладает отношением порядка, называется упорядоченным.
Отношение порядка
антисимметричность
транзитивность
+ рефлексивность
+
Отношение нестрогого порядка ≤
Отношение строгого порядка <
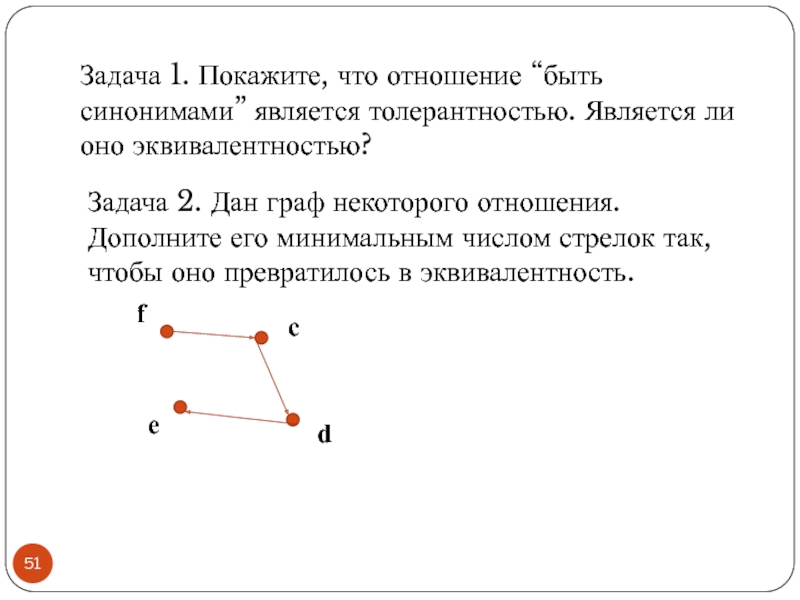
Слайд 51Задача 2. Дан граф некоторого отношения. Дополните его минимальным числом стрелок
f
c
d
e
Задача 1. Покажите, что отношение “быть синонимами” является толерантностью. Является ли оно эквивалентностью?
Слайд 52Задача 3. Назовем два слова сходными, если они состоят из одинакового
Задача 4. Папки в файловой системе компьютера вложены друг в друга, образуя ветвящуюся структуру. Определить вид отношения «вложенности».
Задача 5. Определить вид отношения