- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Диаграмма Вороного презентация
Содержание
- 6. Наверно, многие заметили что то общее между
- 7. Диаграмма Вороного
- 9. Перед тем, как начать разбираться, что такое
- 11. Именно из выпуклых многоугольников и будет состоять
- 12. Что такое диаграмма Вороного? Это разбиение
- 14. Немного истории Первое использование этой диаграммы встречается
- 15. Спустя два века, известный немецкий математик
- 16. В1908 году русский математик Георгий Феодосьевич
- 17. Применение диаграммы Воронова Применение диаграммы очень обширно,
- 18. Геолокационный софт использует диаграммы Вороного. Геолокационные рекомендательные
- 19. Диаграмма часто используется дизайнерами и архитекторами
- 20. Heydar Aliyev Center / Zaha Hadid Architects
- 21. Метод Вороного был усовершенствован Борисом Делоне. Который
- 24. Эстетика параметризма проникла и в современные
- 27. Алгоритмы построения Алгоритм построения диаграммы Вороного
Слайд 6Наверно, многие заметили что то общее между картинками показанными ранее. Некий
часто встречающийся узор, органическую структуру в клетках, окраске животных, архитектуре.
Все эти структуры созданы с помощью популярной во многих областях
диаграммы Вороного
Она позволяет легко создавать параметрические (задаваемые набором легко изменяемых параметров) структуры, которые будут выглядеть, как органические формы.
Все эти структуры созданы с помощью популярной во многих областях
диаграммы Вороного
Она позволяет легко создавать параметрические (задаваемые набором легко изменяемых параметров) структуры, которые будут выглядеть, как органические формы.
Слайд 9Перед тем, как начать разбираться, что такое — диаграмма Вороного, вспомним
некоторые понятия нужных нам геометрических объектов:
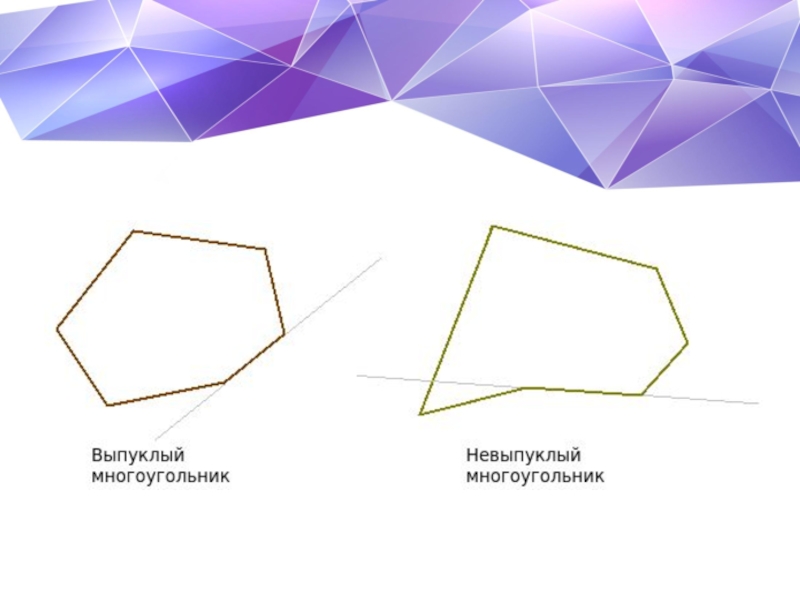
Простой многоугольник — это многоугольник без самопересечений. В диаграмме используются именно они. Невыпуклый многоугольник — это многоугольник, в котором найдутся такие две вершины, что через них проводится прямая, пересекающая данный многоугольник где-либо ещё, кроме ребра, соединяющего эти вершины Выпуклый многоугольник — это многоугольник, у которого продолжения сторон не пересекают других его сторон
Простой многоугольник — это многоугольник без самопересечений. В диаграмме используются именно они. Невыпуклый многоугольник — это многоугольник, в котором найдутся такие две вершины, что через них проводится прямая, пересекающая данный многоугольник где-либо ещё, кроме ребра, соединяющего эти вершины Выпуклый многоугольник — это многоугольник, у которого продолжения сторон не пересекают других его сторон
Основные понятия
Слайд 11Именно из выпуклых многоугольников и будет состоять диаграмма. Почему именно из
выпуклых? Потому что они являются ничем иным, как пересечением полуплоскостей, которые являются выпуклыми фигурами.
Раз уж мы начали говорить про полуплоскости, то можно плавно перейти и к самой диаграмме — она состоит из так называемых локусов — областей, в которых присутствуют все точки, которые находятся ближе к данной точке, чем ко всем остальным. В диаграмме Вороного локусы являются выпуклыми многоугольниками.
Точку, для которой строится локус, называют сайтом (site).
Раз уж мы начали говорить про полуплоскости, то можно плавно перейти и к самой диаграмме — она состоит из так называемых локусов — областей, в которых присутствуют все точки, которые находятся ближе к данной точке, чем ко всем остальным. В диаграмме Вороного локусы являются выпуклыми многоугольниками.
Точку, для которой строится локус, называют сайтом (site).
Слайд 12Что такое диаграмма Вороного?
Это разбиение плоскости с заданными «главными» точками на
такие участки (локусы) для каждой «главной» точки (сайту), что все точки внутри каждого такого участка будут ближе к «главной» точке , чем к любой другой. Попробуем понять это, начертив — диаграмму Вороного.
Слайд 14Немного истории
Первое использование этой диаграммы встречается в труде Рене Декарта (1596-1650)
«Начала философии» (1644). Декарт предложил деление Вселенной на зоны гравитационного влияния звезд.
Слайд 15
Спустя два века, известный немецкий математик Иоганн Петер Густав Лежён-Дирихле (1805
— 1859) ввел диаграммы для двух- и трехмерного случаев. Поэтому их иногда называют диаграммами Дирихле
Слайд 16
В1908 году русский математик Георгий Феодосьевич Вороной (16 апреля 1868 —
7 ноября 1908) описал эту диаграмму для пространств больших размерностей, с тех пор диаграмма носит его фамилию.
Слайд 17Применение диаграммы Воронова
Применение диаграммы очень обширно, затронем только несколько примеров:
диаграмма в
картографии — для очерчивания границ регионов и дальнейшего анализа на их основе. Да и вообще, любые географические диаграммы, показывающие распределение чего либо, можно наглядно можно проиллюстрировать с помощью раскрашенных диаграмм Вороного, и там будет виден переход нужного нам показателя (например, температуры)
Слайд 18Геолокационный софт использует диаграммы Вороного. Геолокационные рекомендательные системы могут использовать диаграмму
Вороного для определения, например, ближайшего к вам продуктового магазина, для различного поиска и анализа местоположения.
широко используется диаграмма при моделировании органических систем в биологии.
В промышленном дизайне
широко используется диаграмма при моделировании органических систем в биологии.
В промышленном дизайне
Слайд 19 Диаграмма часто используется дизайнерами и архитекторами для облегчения и украшения
конструкций. Органические формы хорошо сочетаются с «зелеными» стенами, выглядят одновременно природно и футуристично.
Параметризм стиль в котором используется диаграмма.
Развитие компьютерных технологий и увеличение вычислительных мощностей компьютеров открывают огромные возможности для дальнейшего развития параметрического дизайна. С их помощью архитекторы, дизайнеры, скульпторы и художники обретают больше свободы в создании сложных форм.
Параметризм стиль в котором используется диаграмма.
Развитие компьютерных технологий и увеличение вычислительных мощностей компьютеров открывают огромные возможности для дальнейшего развития параметрического дизайна. С их помощью архитекторы, дизайнеры, скульпторы и художники обретают больше свободы в создании сложных форм.
Слайд 21Метод Вороного был усовершенствован Борисом Делоне. Который ввел понятие триангуляции. С
помощью триангуляции Делоне можно описать практически любой «естественный» алгоритм. Мощность современных компьютеров уже достаточна для использования так называемых генетических алгоритмов с миллионами возможных комбинаций параметров. То, что получается на выходе, скорее напоминает нерукотворные творения
Слайд 24
Эстетика параметризма проникла и в современные интерьеры. Плавные лини, изогнутые геометрические
паттерны создают ощущение сюрреализма. Стены и потолки перестают быть плоскими и статичными. Они открывают портал в иные измерения, обнажая кривизну пространства и времени в которых мы живем.
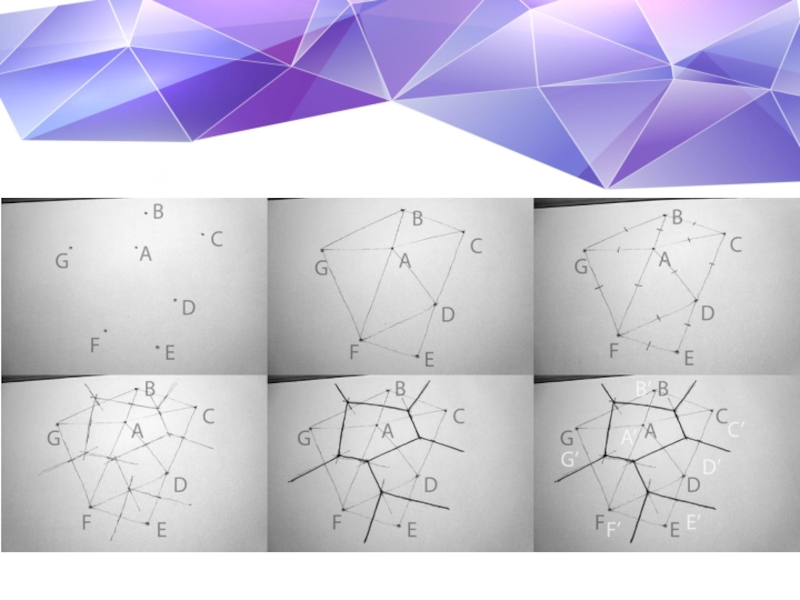
Слайд 27Алгоритмы построения
Алгоритм построения диаграммы Вороного «в лоб»
Алгоритм построения диаграммы Вороного путём
пересечения полуплоскостей
Алгоритм Форчуна построения диаграммы Вороного на плоскости
Рекурсивный алгоритм построения диаграммы Вороного
Алгоритм Форчуна построения диаграммы Вороного на плоскости
Рекурсивный алгоритм построения диаграммы Вороного