- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное диференцирование презентация
Содержание
- 1. Численное диференцирование
- 2. План Численное дифференцирование функций, заданных аналитически Численное
- 3. Разностная схема первого порядка точности Производная
- 4. Симметричная разностная схема второго порядка Ряд
- 5. Симметричная разностная схема для второй производной
- 6. Продифференцировать численно функцию с применением
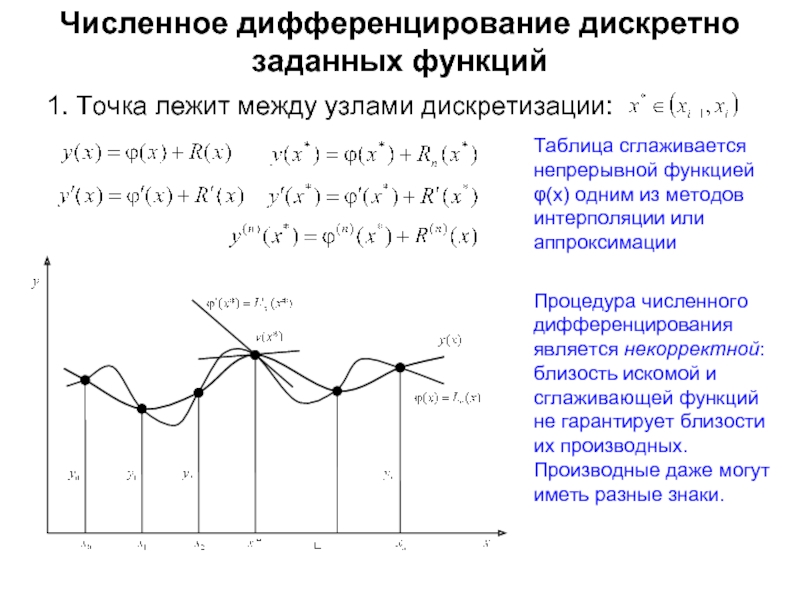
- 7. Численное дифференцирование дискретно заданных функций
- 8. Численное дифференцирование дискретно заданных функций
- 9. Численное дифференцирование дискретно заданных функций Вторая
- 10. Метод Рунге уточнения формул численного дифференцирования
Слайд 2План
Численное дифференцирование функций, заданных аналитически
Численное дифференцирование функций, заданных дискретным набором данных
Метод
Литература
Формалев В. Ф., Ревизников Д. Л., Численные методы. –М.: Физматлит, 2004. - 400 с.
Поршнев С.В., Беленкова И.В., Численные методы на базе Mathcad. – СПб.: БХВ-Петербург, 2005. – 464 с.
Слайд 3Разностная схема первого порядка точности
Производная от функции
Простейшая приближенная формула (правосторонняя разностная
Ряд Тейлора
Ошибка приближенной формулы
Левосторонняя разностная схема первого порядка
Формулы точны для полиномов первой степени, т.к. для них
Слайд 4Симметричная разностная схема второго порядка
Ряд Тейлора
Ошибка приближенной формулы
Формула точна для полиномов
Слайд 5Симметричная разностная схема для второй производной
Ряд Тейлора
Ошибка приближенной формулы
Формула точна для
Схемы для производных более высоких порядков можно строить аналогично
Альтернативная идея вывода
Слайд 6Продифференцировать численно функцию
с применением правосторонней и симметричной разностных формул для первой
Пример
Слайд 7Численное дифференцирование дискретно заданных функций
Таблица сглаживается непрерывной функцией φ(x) одним
Процедура численного дифференцирования является некорректной: близость искомой и сглаживающей функций не гарантирует близости их производных. Производные даже могут иметь разные знаки.
Слайд 8
Численное дифференцирование дискретно заданных функций
Можно использовать аппарат разложения функций в
Отношение конечных разностей справа
Отношение конечных разностей слева
Отношение центральных разностей
Порядком точности метода численного дифференцирования называют показатель степени h в главном члене погрешности
Слайд 9Численное дифференцирование дискретно заданных функций
Вторая производная
Третья производная
Правосторонние разности
Левосторонние
Центральные разности
Центральные разности
Фактически, используется 5 узлов
Используется 4 узла сетки
Четвертая производная
Слайд 10Метод Рунге уточнения формул
численного дифференцирования
Метод p-го порядка
Остаточный член
Вводим
Производная на сетке с шагом kh
Главный член погрешности в узлах исходной сетки
Вычисляем разностную производную на равномерной сетке с шагом h
Метод (p+1)-го порядка в узлах исходной сетки
Уточненная разностная аппроксимация