- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Чётность, нечётность, периодичность функций презентация
Содержание
- 2. График чётной функции симметричен относительно оси
- 3. Четные функции Их графики симметричны относительно оси
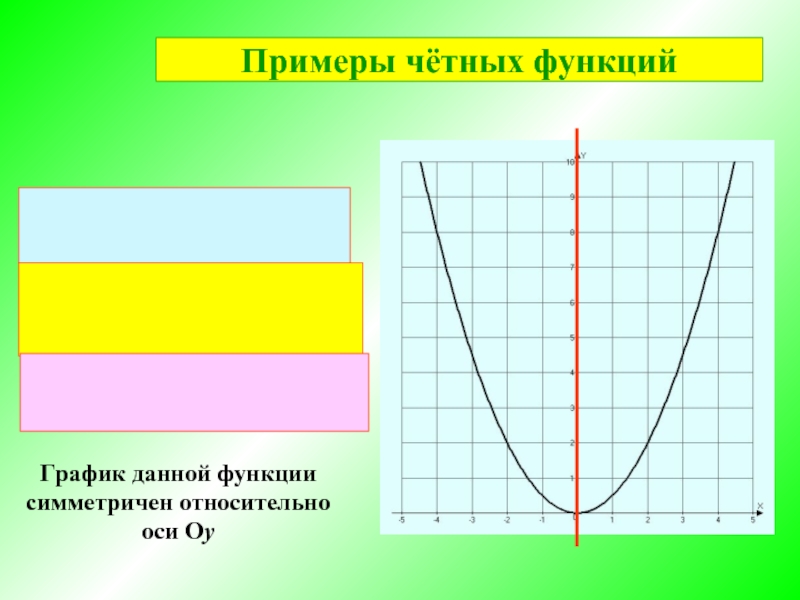
- 4. График данной функции симметричен относительно оси Оу Примеры чётных функций
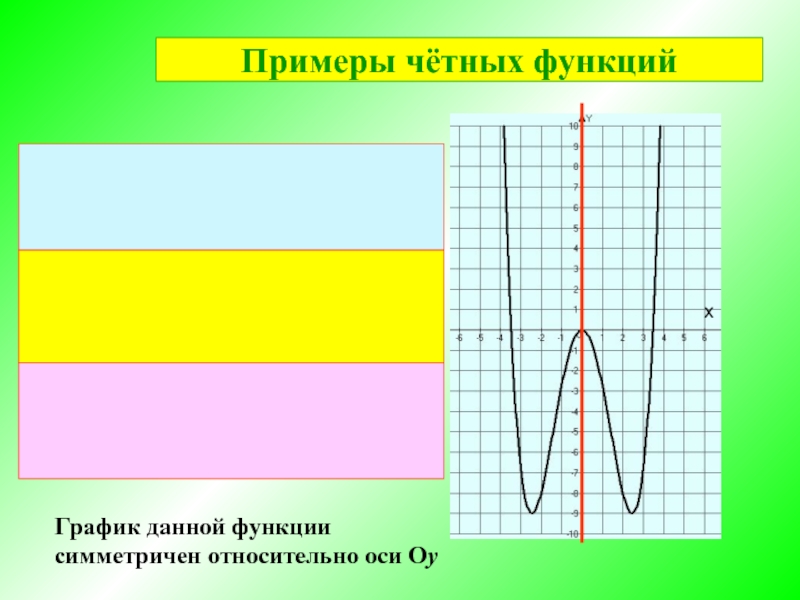
- 5. График данной функции симметричен относительно оси Оу х Примеры чётных функций
- 6. График нечётной функции симметричен относительно начала
- 7. Нечетные функции Их графики симметричны относительно начала
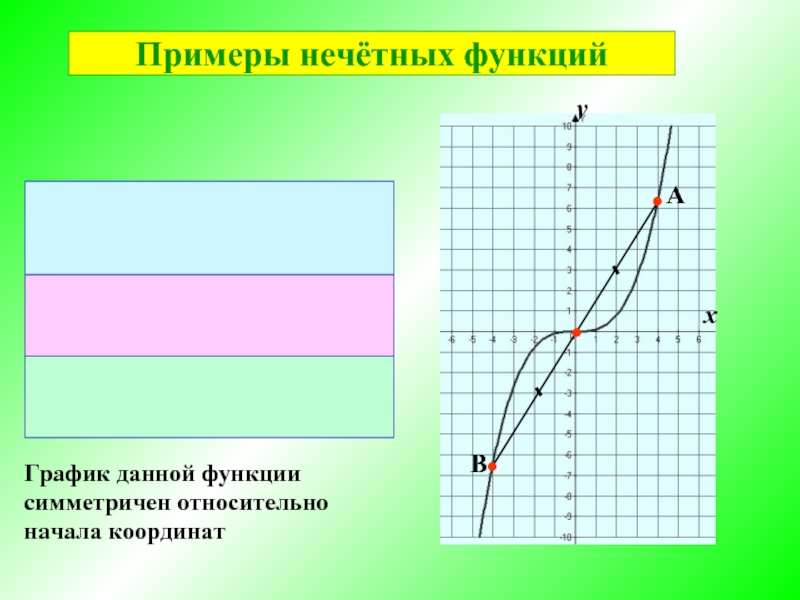
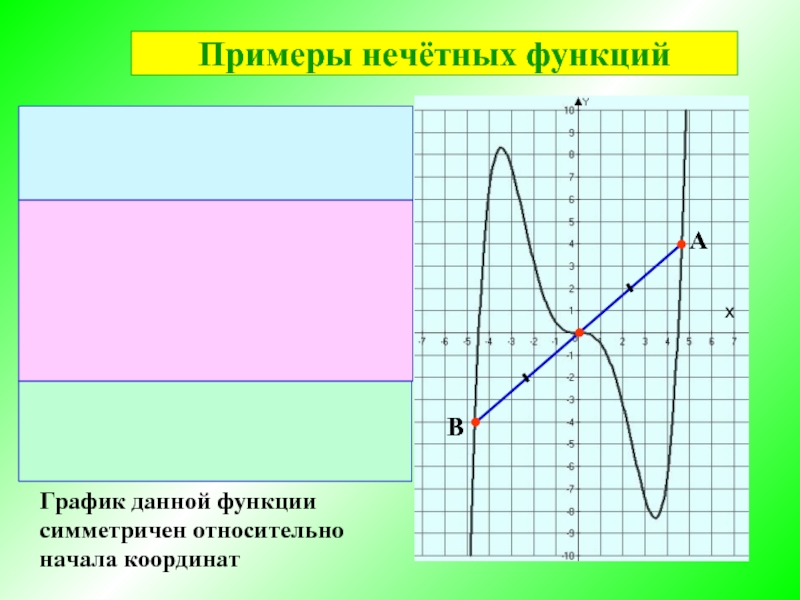
- 8. График данной функции симметричен
- 9. График данной функции симметричен
- 10. Функция называется периодической, если
- 11. Периодические функции График периодической функции состоит из
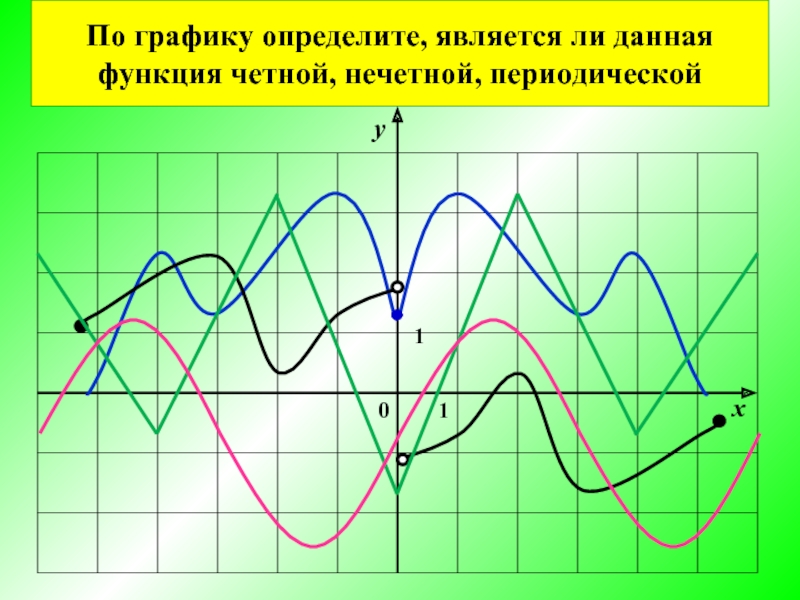
- 12. По графику определите, является ли данная функция четной, нечетной, периодической ●
График чётной функции симметричен относительно оси ОУ Функция у = f (x) с D(f) = X называется чётной, если для любого x Є X есть (‒х) Є X
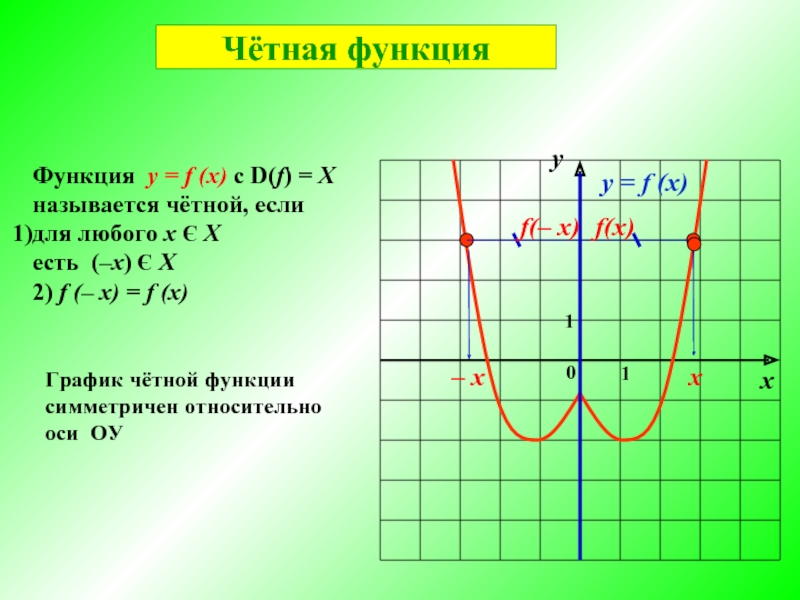
Слайд 2График чётной функции
симметричен относительно
оси ОУ
Функция у = f (x) с
D(f) = X называется чётной, если
для любого x Є X
есть (‒х) Є X
2) f (‒ x) = f (x)
для любого x Є X
есть (‒х) Є X
2) f (‒ x) = f (x)
Чётная функция
х
‒ х
f(х)
f(‒ х)
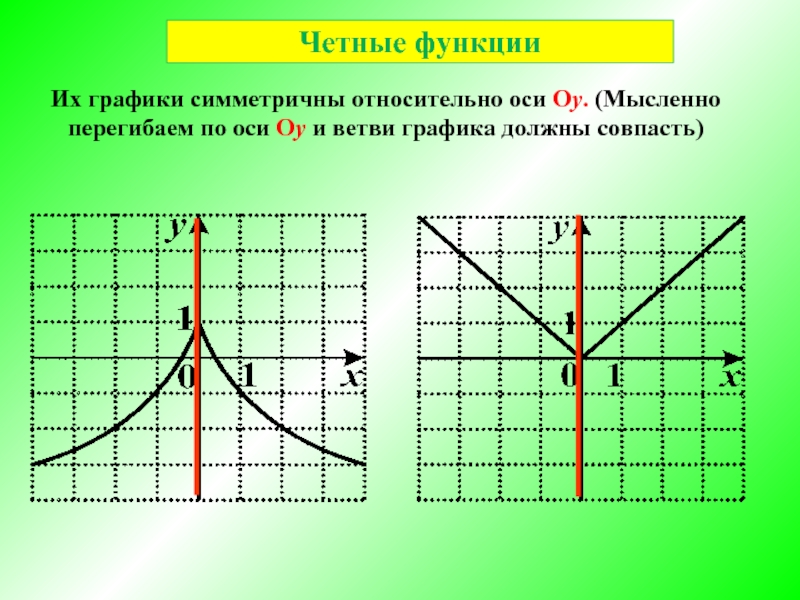
Слайд 3Четные функции
Их графики симметричны относительно оси Oу. (Мысленно перегибаем по оси
Oу и ветви графика должны совпасть)
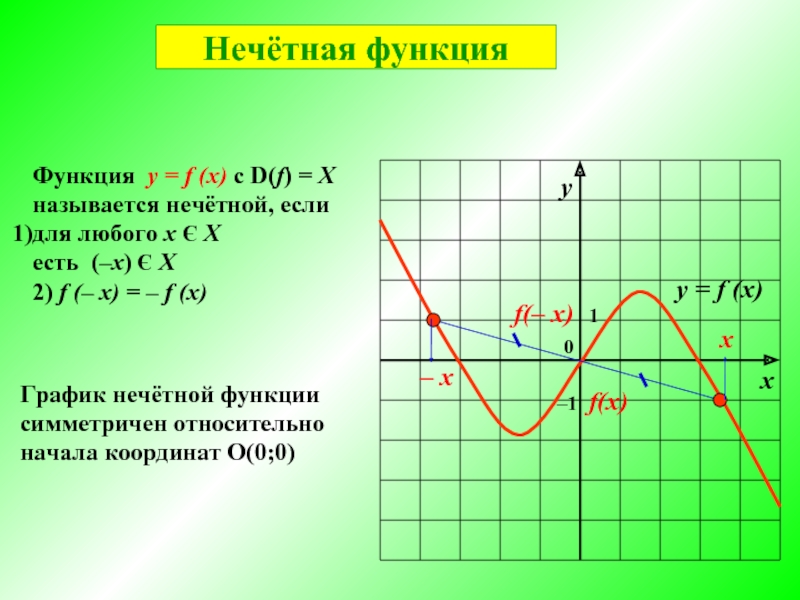
Слайд 6График нечётной функции
симметричен относительно
начала координат О(0;0)
Функция у = f (x)
с D(f) = X называется нечётной, если
для любого x Є X
есть (‒х) Є X
2) f (‒ x) = ‒ f (x)
для любого x Є X
есть (‒х) Є X
2) f (‒ x) = ‒ f (x)
Нечётная функция
х
‒ х
f(‒ х)
f(х)
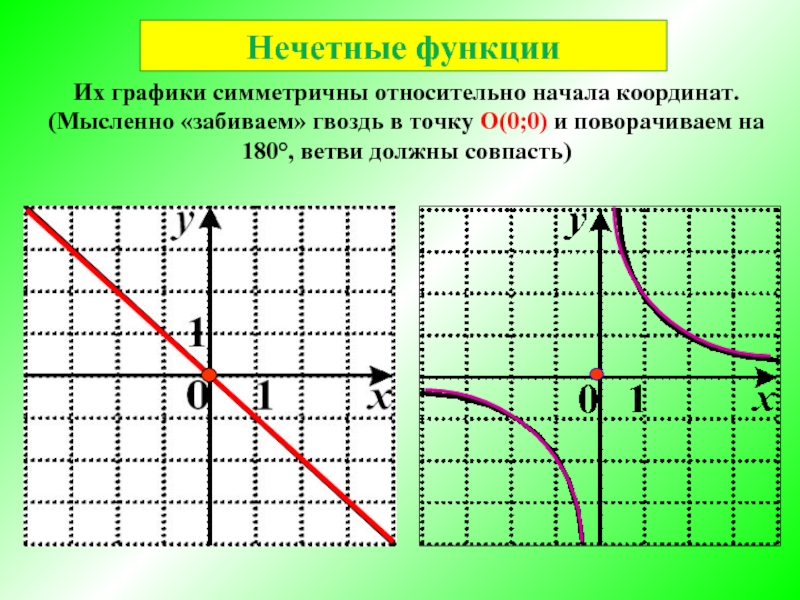
Слайд 7Нечетные функции
Их графики симметричны относительно начала координат. (Мысленно «забиваем» гвоздь в
точку O(0;0) и поворачиваем на 180°, ветви должны совпасть)
Слайд 10
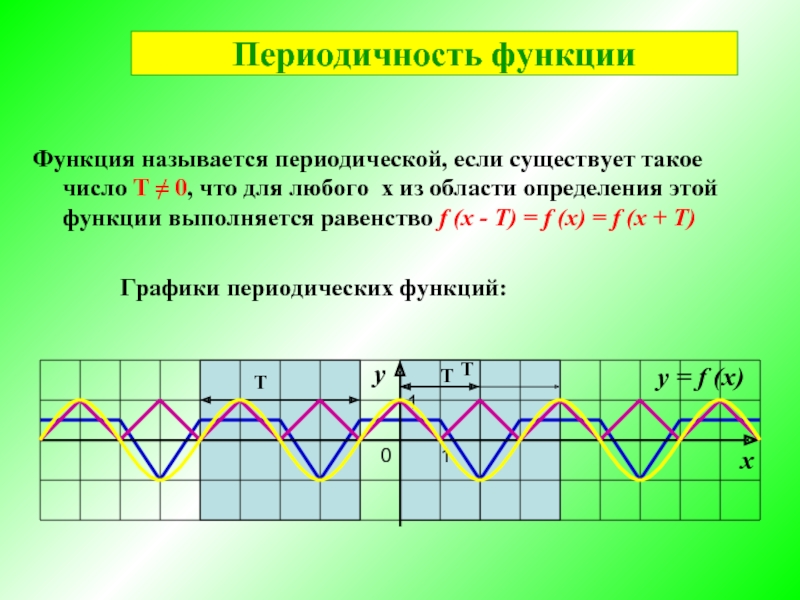
Функция называется периодической, если существует такое число Т ≠ 0, что
для любого х из области определения этой функции выполняется равенство f (x - T) = f (x) = f (x + T)
у = f (x)
Графики периодических функций:
Т
T
T
Периодичность функции
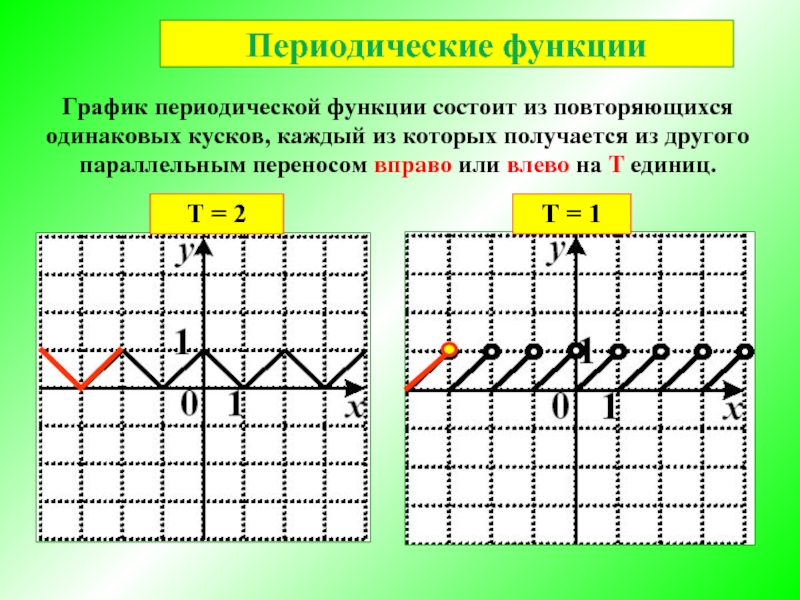
Слайд 11Периодические функции
График периодической функции состоит из повторяющихся одинаковых кусков, каждый из
которых получается из другого параллельным переносом вправо или влево на Т единиц.
Т = 2
Т = 1
