- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовые множества. Комплексные числа презентация
Содержание
- 1. Числовые множества. Комплексные числа
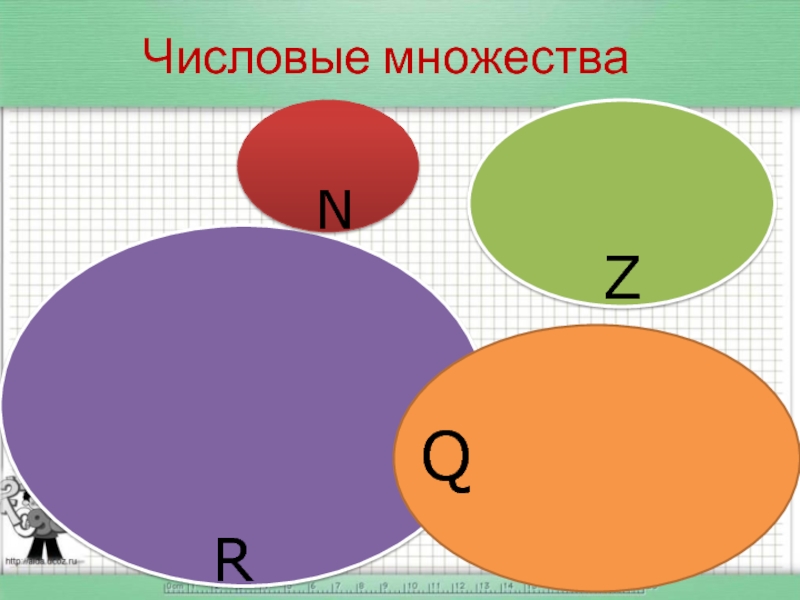
- 2. Числовые множества
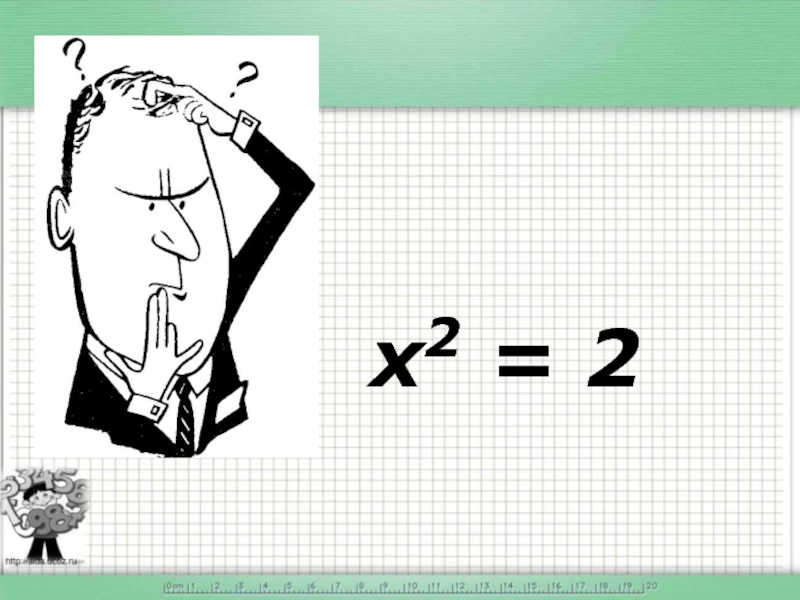
- 3. x2 = 2
- 5. x2 +4 = 0 Нет решения в IR
- 6. Решите уравнения: Вариант I Вариант II
- 7. x2 = -1 i – мнимая единица i2 = -1
- 8. a,b – любые действительные числа Если а
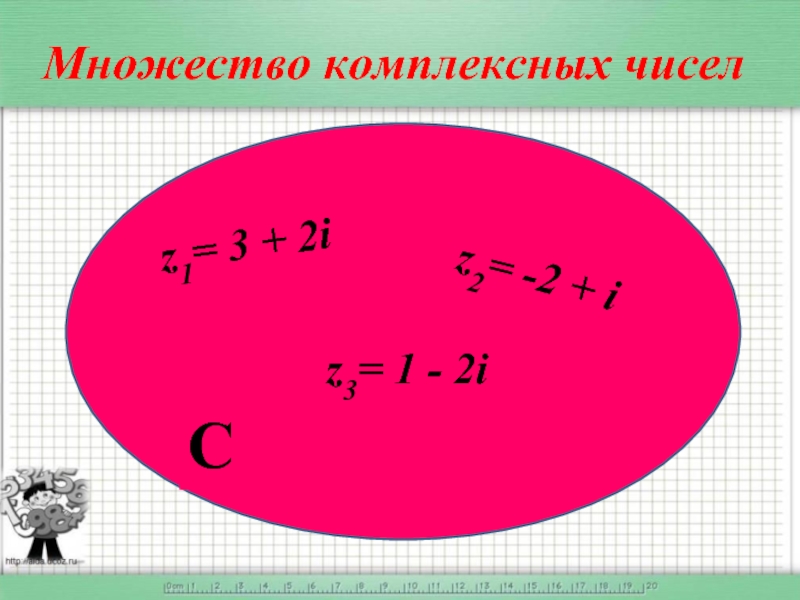
- 9. Множество комплексных чисел
- 10. СУММА z1 = a1 + b1i z2
- 11. а)Z1 =5+4i
- 12. РАЗНОСТЬ Z1 = a1+b1i Z2 = a2+b2i
- 13. РАЗНОСТЬ z1 = a1 + b1i z2
- 14. а)Z1 =5+4i
- 15. Возведение в степень Вычислить: а) i3=
- 16. Самостоятельная работа Для комплексных чисел z1 и
- 17. Произведение Произведением комплексных чисел является комплексное число:
- 18. Если у комплексного числа сохранить действительную часть
- 19. Деление Для того, чтобы разделить два
- 20. Геометрическое изображение комплексных чисел. Рассмотрим плоскость с
- 21. Часто бывает удобно рассматривать на комплексной плоскости
- 22. Модулем (абсолютной величиной) комплексного числа называется длина
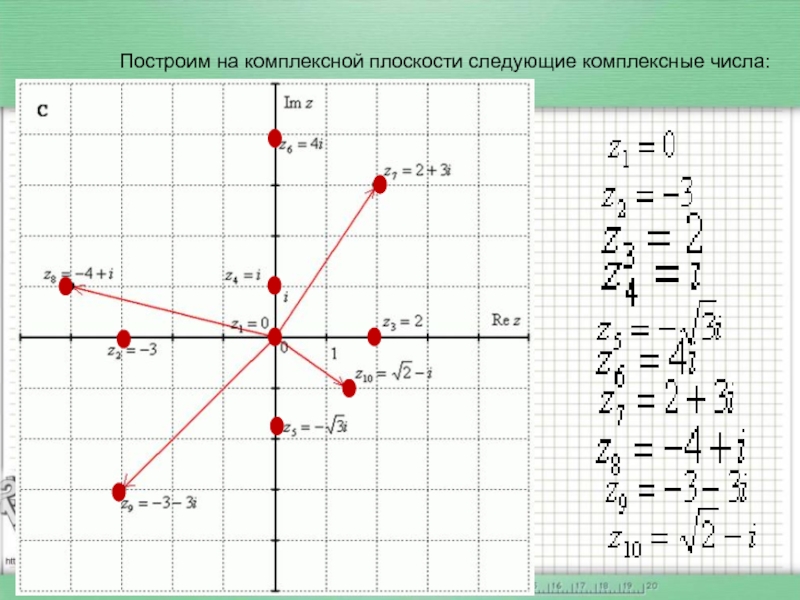
- 23. Построим на комплексной плоскости следующие комплексные числа:
- 24. Модулем комплексного числа z называется расстояние от
Слайд 6Решите уравнения:
Вариант I
Вариант II
Решения нет
во множестве действительных чисел!!!!!
x2 +1 = 0
x2 +9 = 0
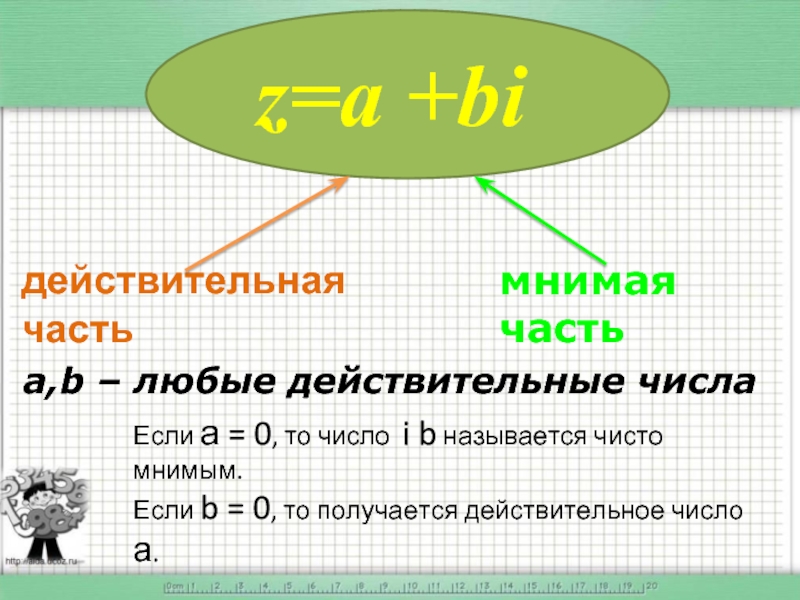
Слайд 8a,b – любые действительные числа
Если а = 0, то число i
Если b = 0, то получается действительное число а.
Слайд 16Самостоятельная работа
Для комплексных чисел z1 и z2 найдите их сумму z1
z1 = 1+i, z2 = -1+2i;
Ответ:
Слайд 18Если у комплексного числа сохранить действительную часть и поменять знак у
комплексное число;
сопряженное число.
Сопряженные числа
Слайд 19Деление
Для того, чтобы разделить два комплексных числа, нужно делимое и делитель
Слайд 20Геометрическое изображение комплексных чисел.
Рассмотрим плоскость с прямоугольной системой
координат. Каждому комплексному
Такая плоскость называется комплексной.
Действительная часть числа на ней занимает
горизонтальную ось, мнимая часть изображается на вертикальной оси; по этой причине горизонтальная и вертикальная оси
называются соответственно вещественной и
мнимой осями.
Вещественная ось
Мнимая ось
Слайд 21Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат,
Геометрическое изображение комплексных чисел.
модул
аргумент
Слайд 22Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной
Модуль комплексного числа z обозначается |z| и определяется выражением
Часто обозначается буквами r или ρ.
Геометрическое изображение комплексных чисел.
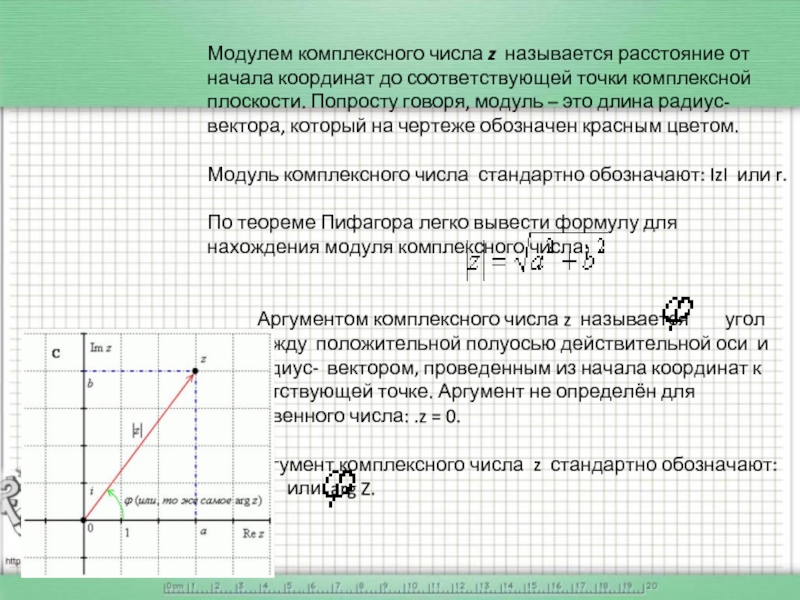
Слайд 24Модулем комплексного числа z называется расстояние от начала координат до соответствующей
Модуль комплексного числа стандартно обозначают: IzI или r.
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа:
Аргументом комплексного числа z называется угол между положительной полуосью действительной оси и радиус- вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .z = 0.
Аргумент комплексного числа z стандартно обозначают: или arg Z.