квазилинейной системы уравнений 1 порядка.
2.Характеристическая форма гиперболической системы уравнений. Инварианты Римана
3. Системы законов сохранения в интегральной и дифференциальной форме
4. Примеры гиперболических систем уравнений в механике
5. Симметризация законов сохранения. Энтропия.
6. Волны Римана
7. Истинно нелинейные и слабо нелинейные семейства характеристик
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное решение гиперболических систем уравнений презентация
Содержание
- 1. Численное решение гиперболических систем уравнений
- 2. Определение гиперболической квазилинейной системы уравнений 1
- 3. Система
- 4. Инварианты Римана Пусть lk зависит только от
- 5. Пример. 1D система уравнений газовой динамики Характеристическая
- 6. для дифференцируемых потоков Интегральная форма уравнений
- 7. Пусть система уравнений записывается в виде
- 8. Дополнительный закон сохранения есть следствие системы уравнений
- 9. Пример. 1D система уравнений мелкой воды используя дополнительный закон сохранения записать систему в симметричной форме.
- 10. Уравнения Эйлера (гидродинамика)
- 11. Уравнения релятивистской гидродинамики Сохранение энергии-импульса Тензор энергии-импульса
- 12. Уравнения релятивистской гидродинамики вектор консервативных переменных
- 13. Уравнения идеальной МГД
- 14. Литература Куликовский А.Г. и др.
- 15. Волны Римана - собственное значение матрицы Определение.
- 16. Волны Римана - правый собственный вектор, соответствующий
- 17. Показать, что скалярное произведение невырожденной
- 18. Математические вопросы численного решения гиперболических систем уравнений
- 19. Вектор функция U называется классическим решением краевой
- 21. скорость поверхности контрольного объема в направлении
- 22. В СК, связанной с разрывом Wn=0
- 23. Уравнения Эйлера Уравнения релятивистской гидродинамики (СТО)
- 24. Модель Баклея-Леверетта многофазной фильтрации несжимаемых жидкостей
- 25. В задаче Баклея-Леверетта отношение вязкости вытесняемой жидкости
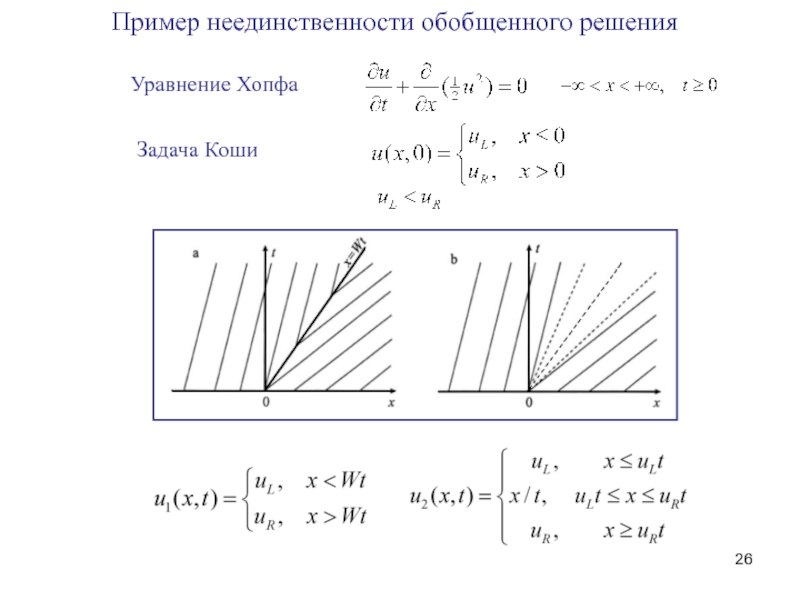
- 26. Пример неединственности обобщенного решения Уравнение Хопфа Задача Коши
- 27. Энтропийное решение потребуем дополнительно - поток
- 28. x t q r Условие эволюционности разрыва
- 29. Метод малой вязкости Скалярный пример (Теорема
- 30. 0 1 2 3 Ударные волны в
- 31. Решение о вязкой структуре ударной волны не
- 32. Задача Римана о распаде разрыва Задача Коши
- 33. Решение задачи Римана о распаде разрыва для
- 34. Точное решение задачи Римана о распаде произвольного
- 35. Решение задачи Римана в скалярном случае
- 36. Математические вопросы численного решения гиперболических систем уравнений 13. Численный метод Годунова.
- 37. Численный метод Годунова (1D) 1. Консервативная
- 38. Численный метод Годунова Система уравнений в
- 39. В случае декартовой СК (x,y) и равномерной
- 40. Метод Годунова для линейной гиперболической системы
- 41. Эквивалентная запись схемы в терминах потоков
- 42. Свойства схемы первого порядка “разность против потока”
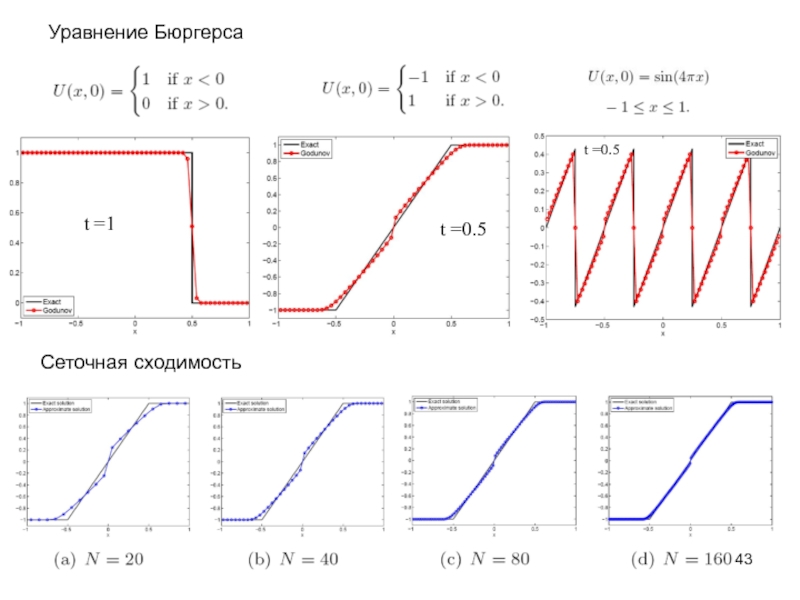
- 43. t =1 t =0.5 t =0.5 Сеточная сходимость Уравнение Бюргерса
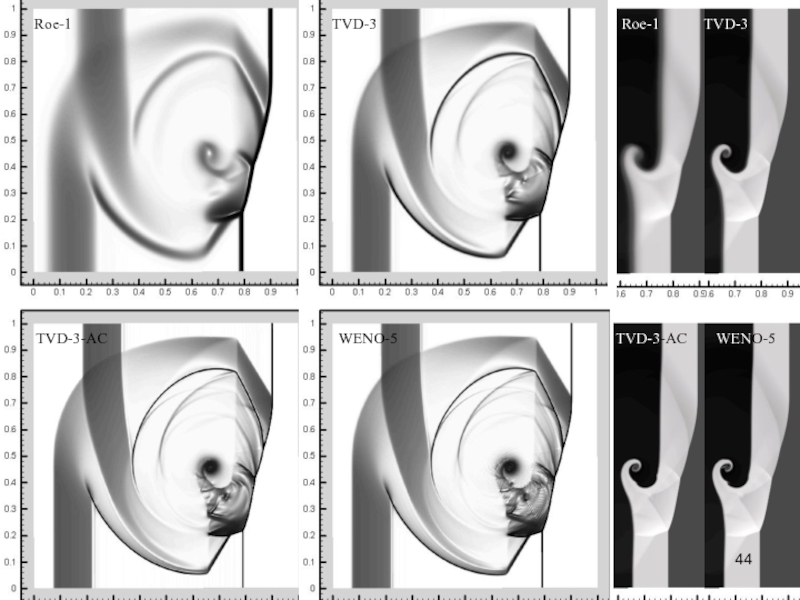
- 44. Roe-1 TVD-3 TVD-3-AC WENO-5 Roe-1 TVD-3 TVD-3-AC WENO-5
- 45. Математические вопросы численного решения гиперболических систем уравнений
- 46. Метод Роу Требования к матрице A(UL,UR)
- 47. Пример: уравнения Эйлера
- 48. Свойство метода Роу. Пусть левые и правые
- 49. Поток пропорциональный градиенту решения Энтропийная коррекция Хартена
- 51. Метод Хартена-Лакса-ван Лира (HLL) x t dx/dt=SL
- 52. Метод HLLC (C for contact) Toro et
- 53. Метод HLLC (C for contact) Toro et
- 54. Оценки скоростей 1. 2. Оценка с использованием собственных значений осредненной по Роу матрицы Якоби
- 55. Схема Русанова 1. В методе КИР
- 56. Схема Лакса-Фридрихса Если в схеме Русанова положить
- 57. Схема FORCE Дополнительная литература
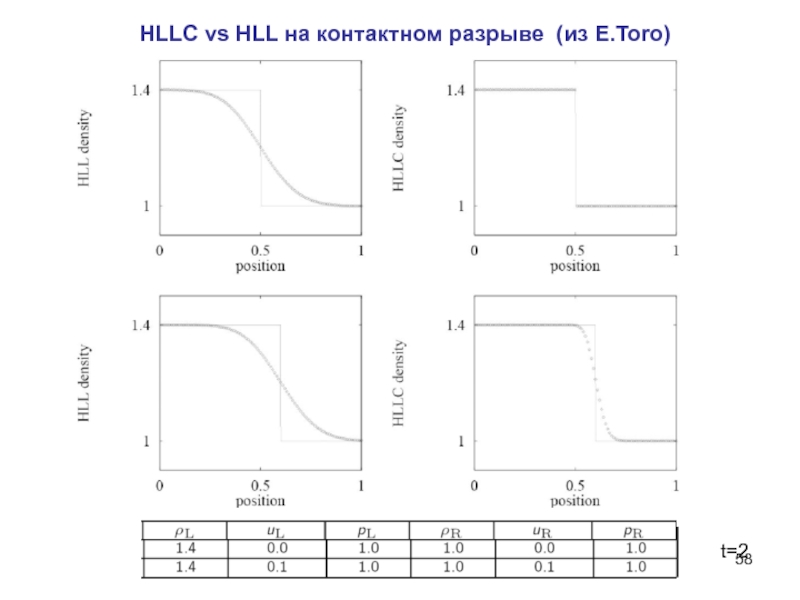
- 58. t=2 HLLC vs HLL на контактном разрыве (из E.Toro)
- 59. Точное решение задачи Римана
- 60. Пример некорректного расчета двойного Маховского
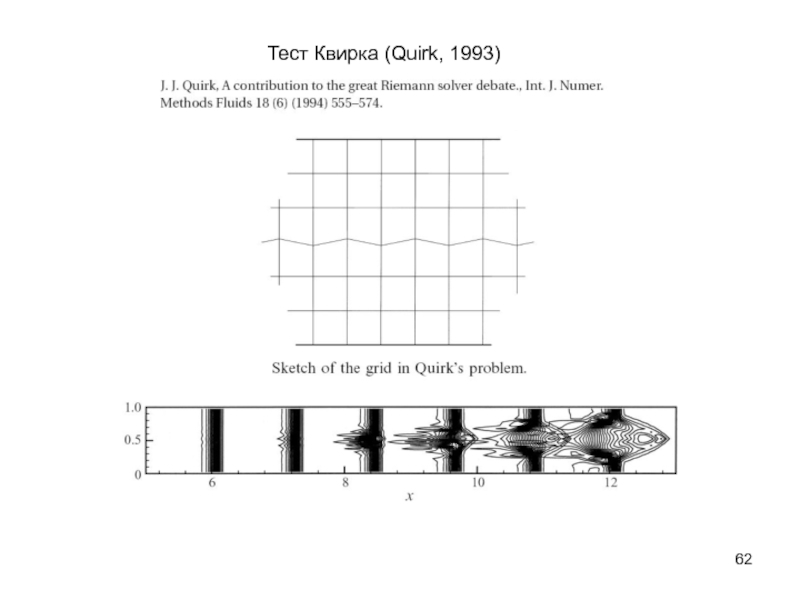
- 62. Тест Квирка (Quirk, 1993)
- 63. Вращательные гибридные методы решения задачи Римана. Уравнения Эйлера
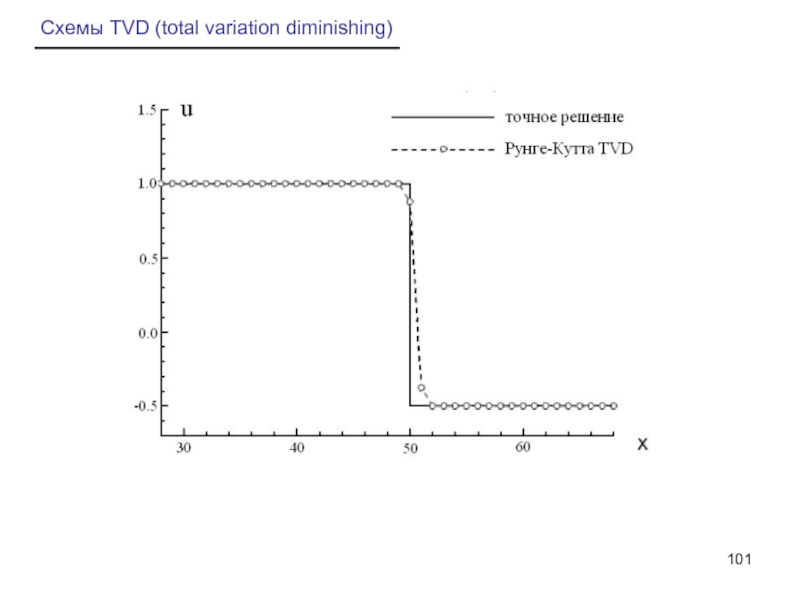
- 64. Шаг интегрирования по времени Метод Рунге-Кутта второго порядка точности Схема TVD с ограничителем van Albada
- 65. При построении вращательного гибридного метода комбинируются различные
- 66. - cтолбец k матрицы собственных векторов Поток Роу:
- 67. Энтропийная коррекция Амплитуды волн Метод HLL В
- 68. Метод Русанова
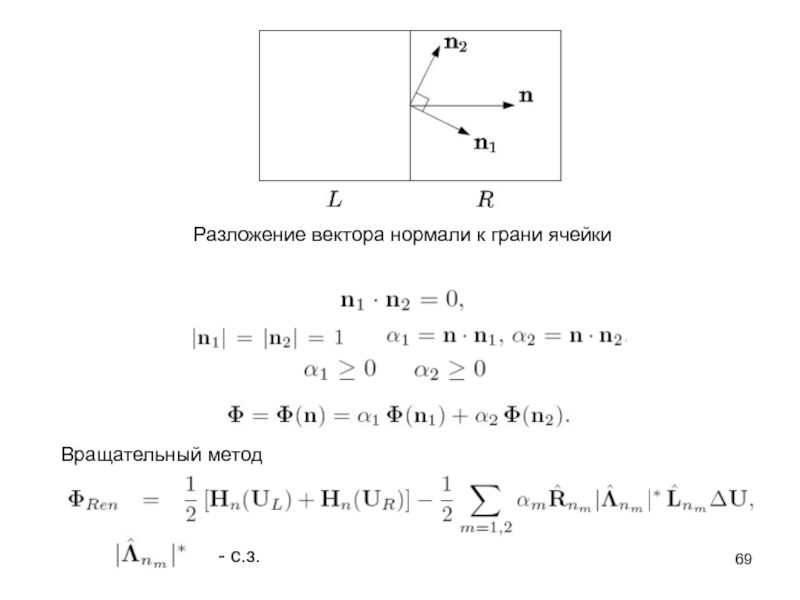
- 69. Разложение вектора нормали к грани ячейки Вращательный метод - с.з.
- 70. Вращательный гибридный метод Roe-Rusanov
- 71. Вращательно гибридный метод Roe-HLL
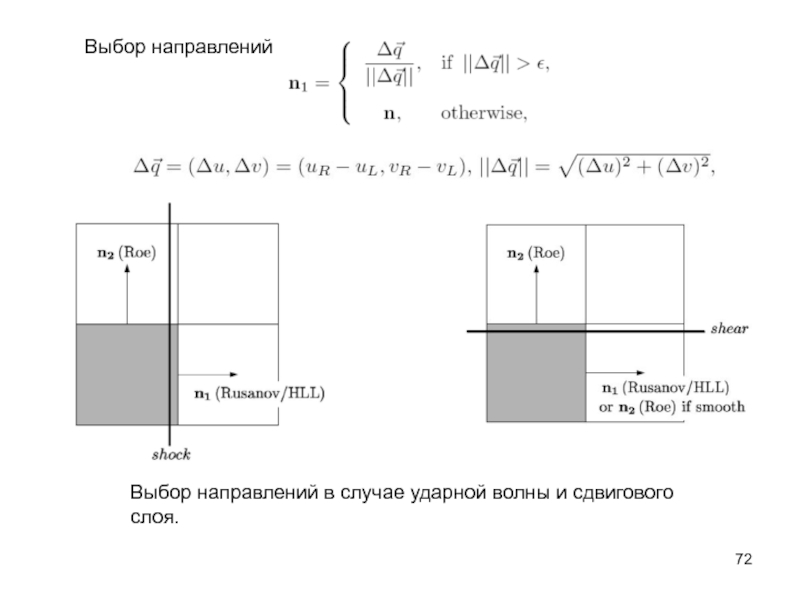
- 72. Выбор направлений Выбор направлений в случае ударной волны и сдвигового слоя.
- 73. Обобщение на трехмерный случай Гибридный поток
- 74. Дополнительная литература Nishikawa, H.; Kitamura, K.
- 75. Некоторые вопросы численного интегрирования систем уравнений гиперболического
- 76. Схемы TVD (total variation diminishing) Монотонные схемы.
- 77. Схемы TVD (total variation diminishing) Теорема (Harten,
- 78. Схемы TVD (total variation diminishing) - все
- 79. Схемы TVD (total variation diminishing) Основная идея:
- 80. Схемы TVD (total variation diminishing) Линейное уравнение
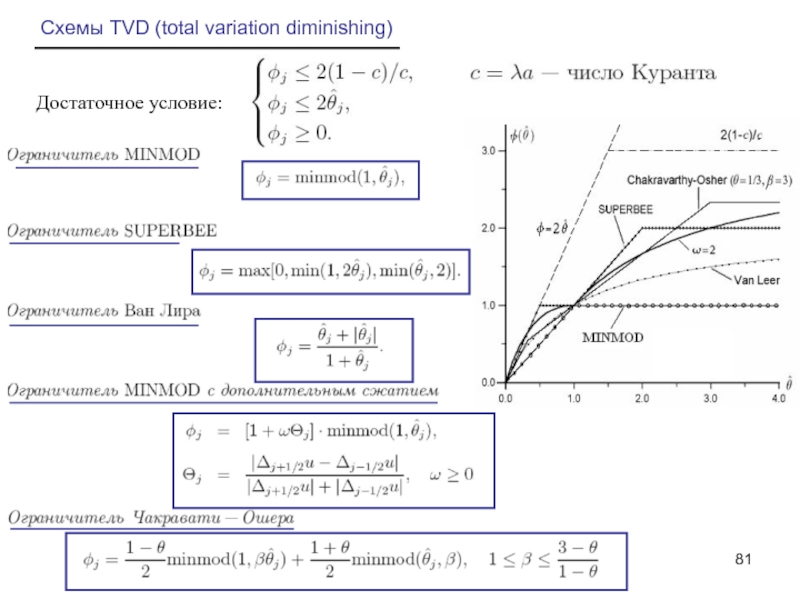
- 81. Схемы TVD (total variation diminishing) Достаточное условие:
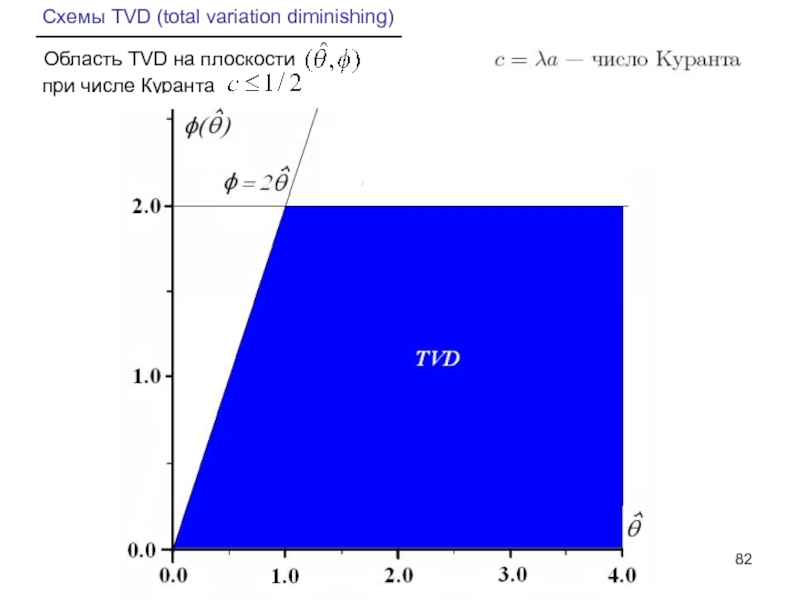
- 82. Схемы TVD (total variation diminishing) Область TVD на плоскости при числе Куранта
- 83. Схемы TVD (total variation diminishing) Область TVD
- 84. Схемы TVD (total variation diminishing) Область TVD
- 85. Схемы TVD (total variation diminishing) Область TVD
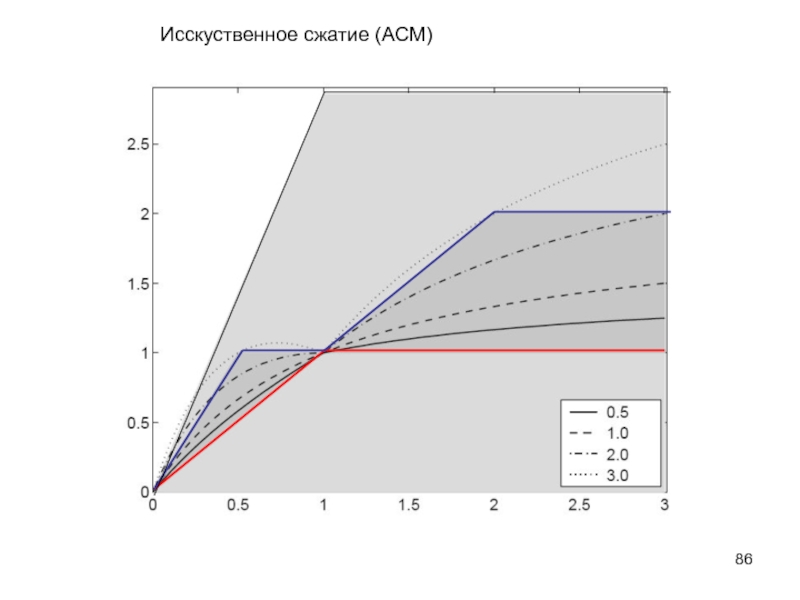
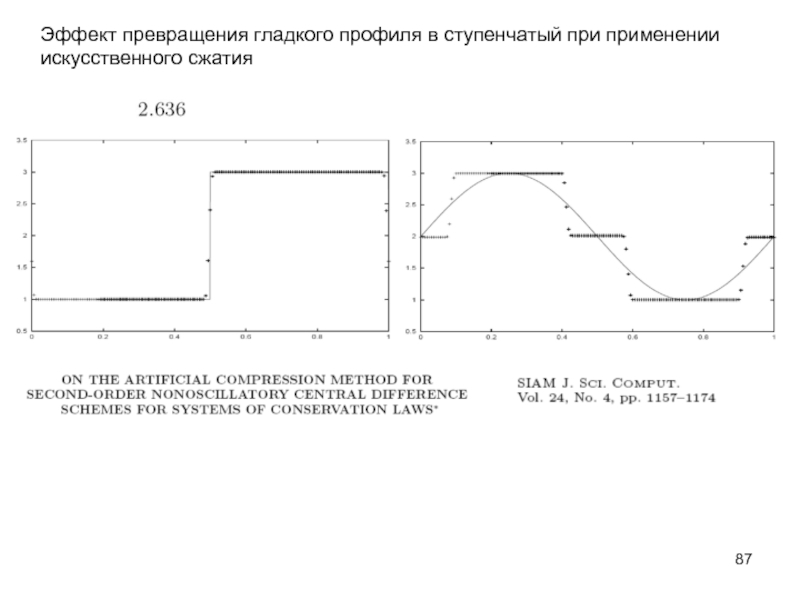
- 86. Исскуственное сжатие (ACM)
- 87. Эффект превращения гладкого профиля в ступенчатый при применении искусственного сжатия
- 88. Схемы TVD (total variation diminishing) 20. Ограничители
- 89. Схемы TVD (total variation diminishing) Ограничители вариации
- 90. Схемы TVD (total variation diminishing) Кусочно-постоянное распределение
- 91. Схемы TVD (total variation diminishing) Применение к
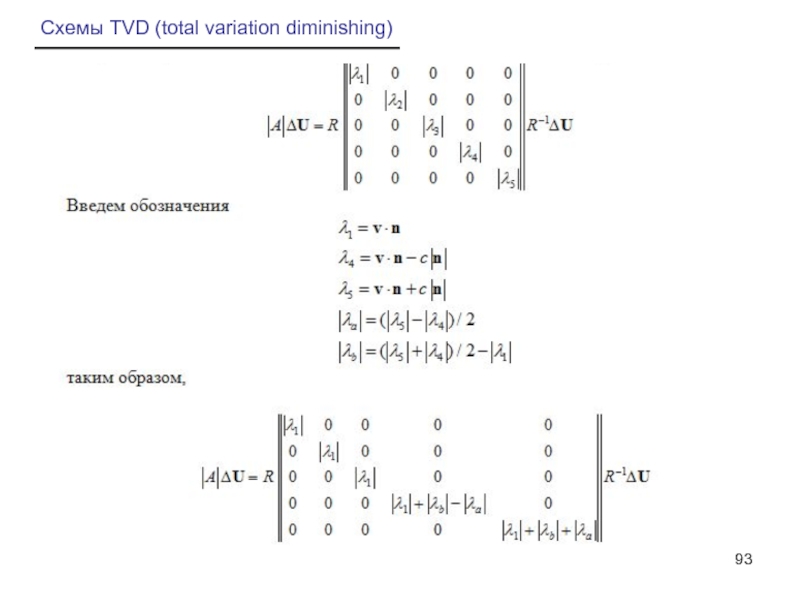
- 92. Схемы TVD (total variation diminishing)
- 93. Схемы TVD (total variation diminishing)
- 94. Схемы TVD (total variation diminishing)
- 95. Пусть
- 96. Интегрирование по времени.
- 97. Пример. Если схема
- 98. Схемы TVD (total variation diminishing) Пример.
- 99. Схемы TVD (total variation diminishing) Сравнение двух
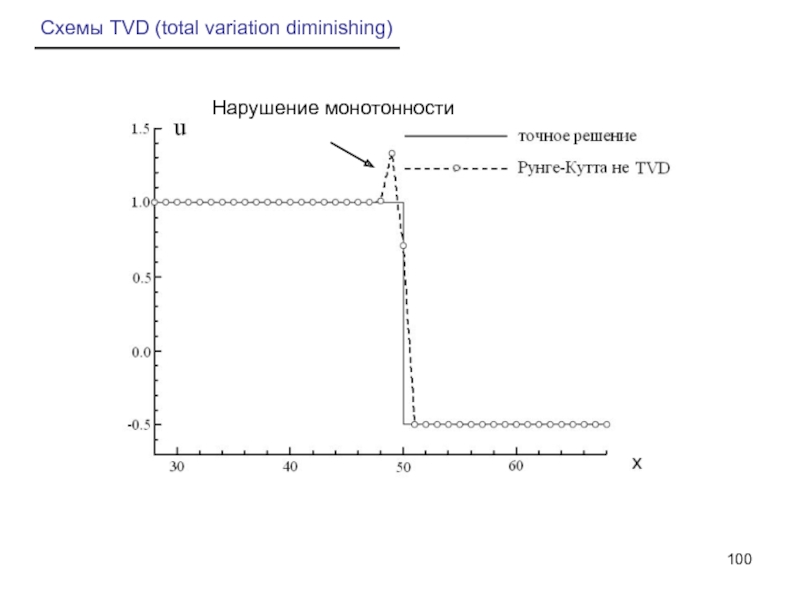
- 100. Схемы TVD (total variation diminishing) Нарушение монотонности
- 101. Схемы TVD (total variation diminishing)
- 102. Некоторые вопросы численного интегрирования систем уравнений гиперболического
- 103. A.Harten, B. Engquist, S.Osher and S. Chakravarthy,
- 104. TVD схемы типа MUSCL Аппроксимация Вычисление
- 105. TVD схемы типа MUSCL Аппроксимация Вычисление
- 106. Построить полином p(x) степени k-1, аппроксимирующий u(x)
- 107. Построить полином p(x) степени k-1, аппроксимирующий u(x)
- 108. Интерполяция Ньютона
- 109. Значение интерполяционного полинома на гранях ячеек
- 110. такой, что разность потоков аппроксимирует производную
- 111. Идея метода ENO: Для увеличения порядка
- 112. Реконструкция решения на гранях ячейки
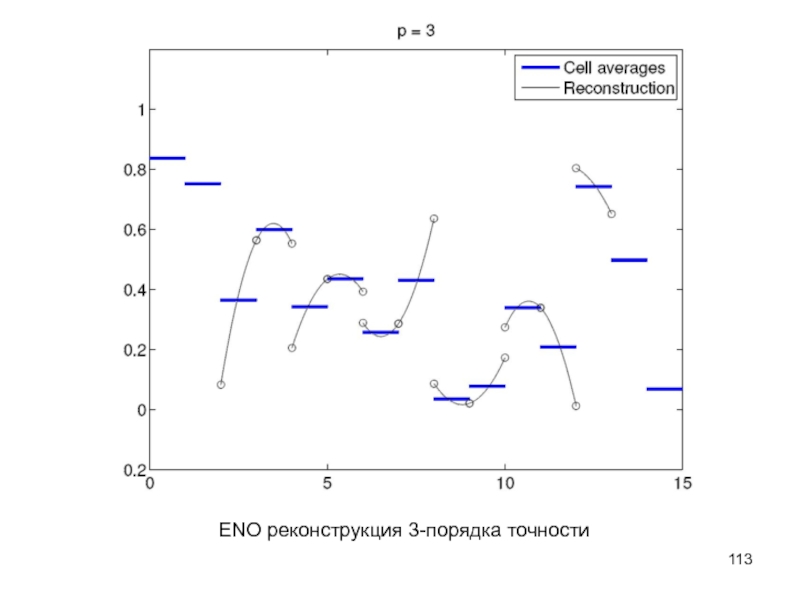
- 113. ENO реконструкция 3-порядка точности
- 114. ENO реконструкция 3-порядка точности на случайном наборе
- 115. p – порядок ENO схемы
- 116. Некоторые вопросы численного интегрирования систем уравнений гиперболического
- 117. Возможности для совершенствования схем ENO 1.
- 118. Шаблоны i-r+k-1
- 119. Основная идея: вместо использования для реконструкции
- 120. Это приводит к следующему представлению для весов
- 121. G.Jiang
- 122. G.Jiang
- 123. WENO реконструкция при k=3
- 124. Линейное уравнение переноса интегрирование
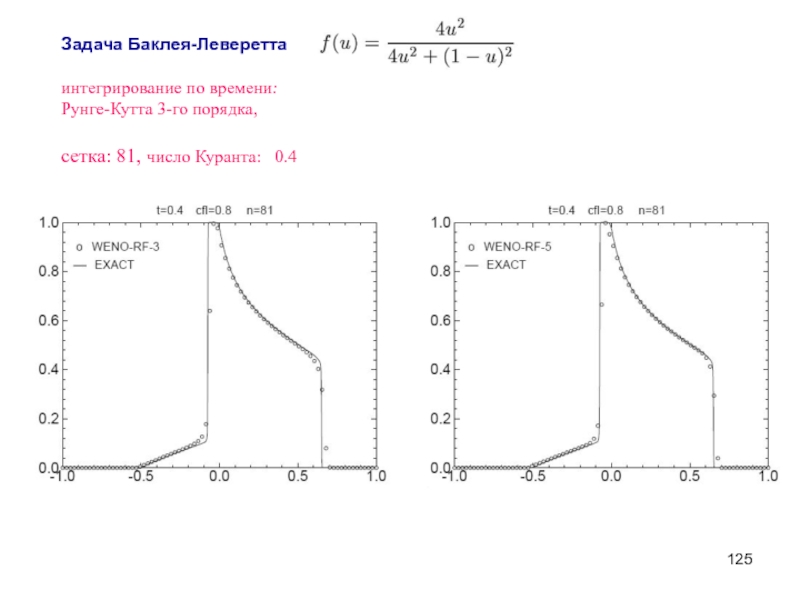
- 125. Задача Баклея-Леверетта интегрирование по времени: Рунге-Кутта
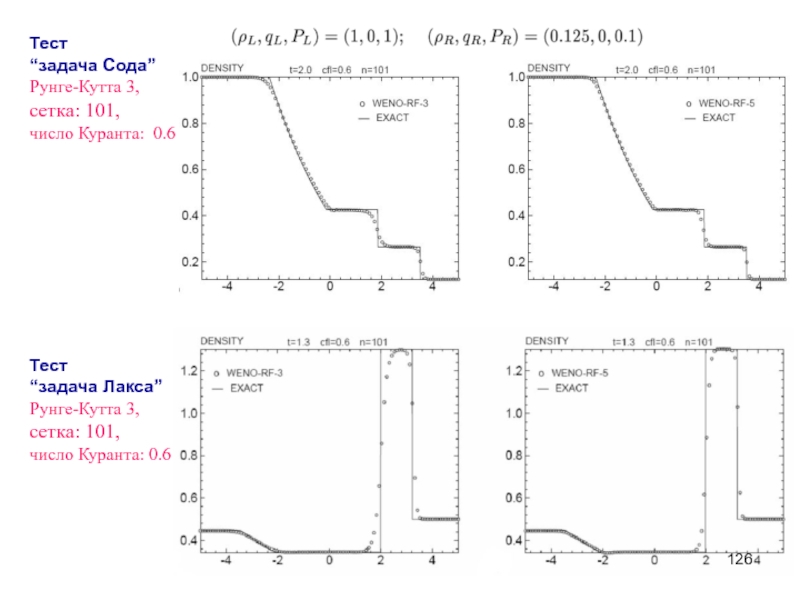
- 126. Тест “задача Сода” Рунге-Кутта 3, сетка:
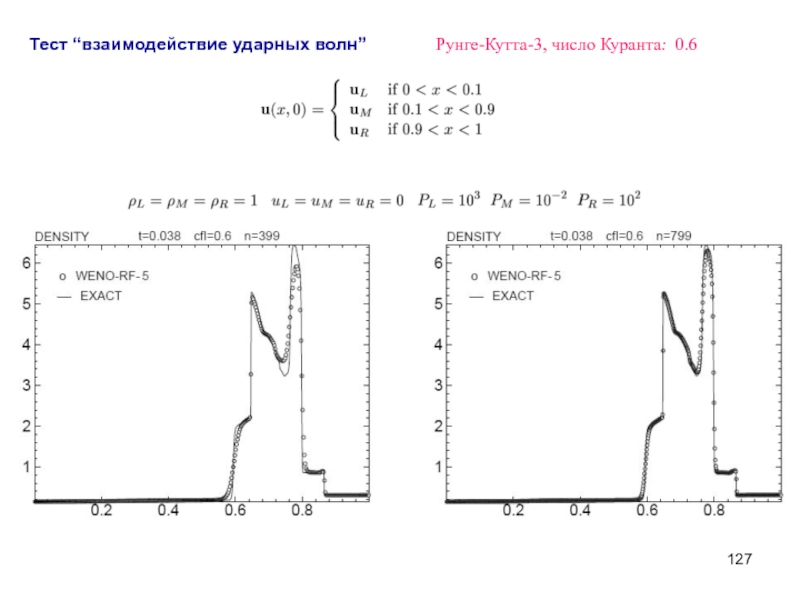
- 127. Тест “взаимодействие ударных волн” Рунге-Кутта-3, число Куранта: 0.6
- 128. Некоторые вопросы численного интегрирования систем уравнений гиперболического
- 129. Литература
- 130. Применение методики локального предобуславливания при решении стационарных задач.
- 131. ≤1 выбирается так, что Параметр 0
- 132. - увеличение шага интегрирования
- 133. Применение предобуславливателя со схемами,
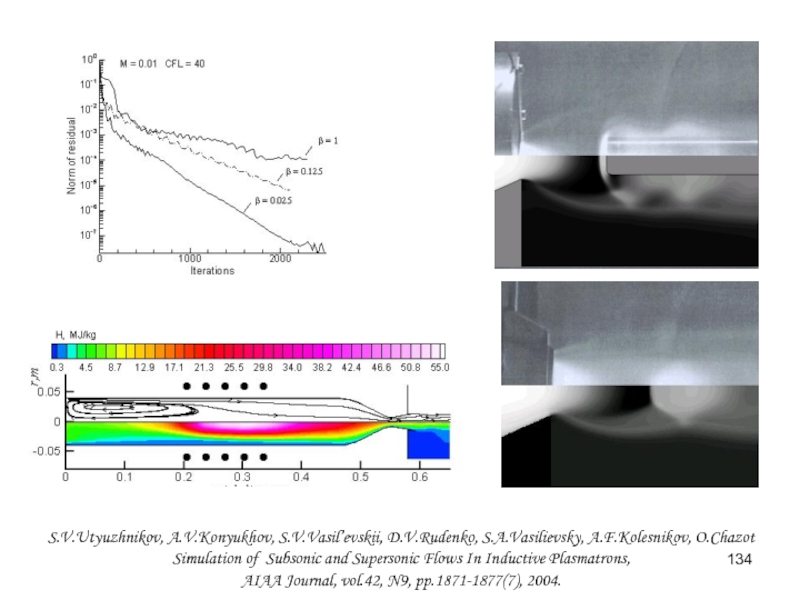
- 134. S.V.Utyuzhnikov, A.V.Konyukhov, S.V.Vasil’evskii, D.V.Rudenko,
Определение гиперболической квазилинейной системы уравнений 1 порядка. (Общий вид квазилинейной системы уравнений первого порядка) Пусть матрица A не особая Введем матрицу P(n):
Слайд 1Математические вопросы численного решения гиперболических систем уравнений
1. Определение гиперболической
Слайд 2 Определение гиперболической квазилинейной системы уравнений 1 порядка.
(Общий вид квазилинейной
системы уравнений первого порядка)
Пусть матрица A не особая
Введем матрицу P(n):
(далее штрих опускаем)
Слайд 3
Система уравнений
описывает одномерный процесс в направлении, заданном вектором
После умножения на
левый собственный вектор lk
Система уравнений в характеристической форме
Слайд 4Инварианты Римана
Пусть lk зависит только от x, t
Соотношения на характеристиках устанавливают
связь между дифференциалами различных переменных в направлении характеристик dx/dt=λk
Интегрирование дифференциальных соотношений на характеристиках в тех случаях, когда оно возможно, приводит к записи системы уравнений в инвариантах Римана
Замечание 1. В случае линейной системы уравнений при f=0, инварианты Римана сохраняют свое значение на характеристиках системы уравнений
Замечание 2. В случае n=2 гиперболическая система всегда может быть расширена, до системы, записанной в инвариантах Римана.
Слайд 5Пример. 1D система уравнений газовой динамики
Характеристическая запись уравнений
Пусть S=const независимо от
x и t,
проинтегрируем соотношения на характеристиках
проинтегрируем соотношения на характеристиках
Инварианты Римана в случае
идеального газа
в напр.
Соотношения между
дифференциалами переменных
в направлении характеристик
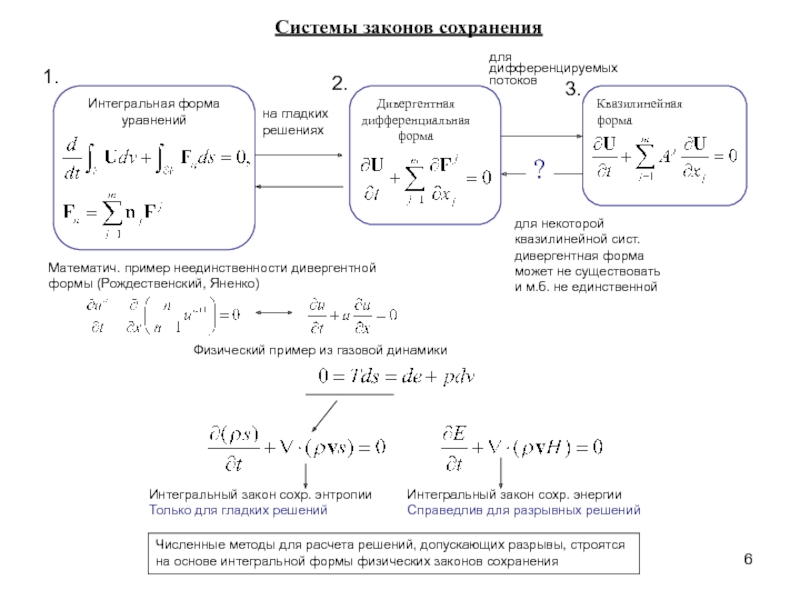
Слайд 6для дифференцируемых потоков
Интегральная форма
уравнений
Дивергентная дифференциальная
форма
Квазилинейная
форма
Системы законов сохранения
1.
2.
3.
на гладких
решениях
?
для некоторой квазилинейной сист. дивергентная форма может не существовать
и м.б. не единственной
Математич. пример неединственности дивергентной формы (Рождественский, Яненко)
Физический пример из газовой динамики
Интегральный закон сохр. энтропии
Только для гладких решений
Интегральный закон сохр. энергии
Справедлив для разрывных решений
Численные методы для расчета решений, допускающих разрывы, строятся на основе интегральной формы физических законов сохранения
Слайд 7 Пусть система уравнений записывается в виде
Система (*) называется симметрической
t-гиперболической системой по Фридрихсу
Система уравнений (*) является гиперболической
где A, Вj – симметричные матрицы, A – положительно определена
(*)
Теорема (Годунов, Фридрихс, Лакс). Пусть система законов сохранения
допускает дополнительный закон сохранения
где - выпуклая функция, тогда система приводится к виду (*)
Симметризация законов сохранения
Слайд 8Дополнительный закон сохранения есть следствие системы уравнений
Подстановка в систему законов сохранения
Квазилинейная форма записи уравнения (***) – симметрическая
t- гиперболическая по Фридрихсу система уравнений
(А, Вj - матрицы Гессе, А – положительно определена)
(преобразование Лежандра)
следовательно
(*)
Определим функции
Преобразование взаимно-однозначно в силу выпуклости
(**)
(*) =>
(**),
выпуклая функция
(***)
Законы сохранения, описывающие изоэнтропические процессы приводят
к гиперболическим системам уравнений
Слайд 9Пример. 1D система уравнений мелкой воды
используя дополнительный закон сохранения
записать систему в
симметричной форме.
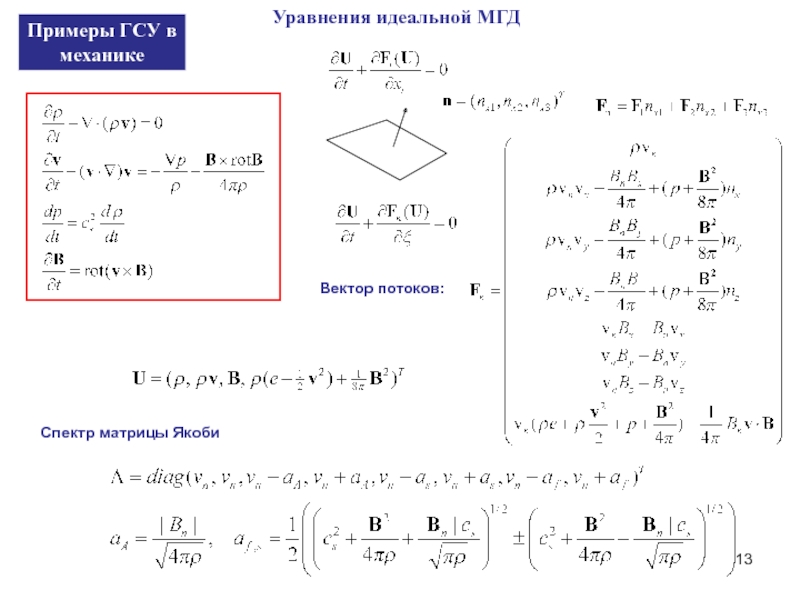
Слайд 10
Уравнения Эйлера (гидродинамика)
Вектор потоков:
Спектр матрицы Якоби
Вектор консервативных переменных:
Примеры ГСУ в
механике
Скорость звука
Слайд 11Уравнения релятивистской гидродинамики
Сохранение энергии-импульса
Тензор энергии-импульса
Примеры ГСУ в
механике
Сохранение скалярной характеристики (заряд, кол-во
частиц, масса покоя)
- фактор Лоренца
4-х вектор скорости
- плотность энтальпии в ССК
4-х дивергенция
- плотность энергии в ССК
- гидростатическое давление
метрический тензор (СТО)
Ландау Л.Д., Лифшиц Е.М. T.VI
Слайд 12Уравнения релятивистской гидродинамики
вектор
консервативных переменных
- потоки
Спектр матрицы
Связь консервативных и
простейших переменных
Примеры
ГСУ в
механике
механике
- скорость звука
Слайд 14 Литература
Куликовский А.Г. и др. Математические вопросы численного решения гиперболических систем
уравнений
Годунов С.К., Роменский Е.И. Элементы механики сплошных сред и законы сохранения
Годунов С.К., Роменский Е.И. Элементы механики сплошных сред и законы сохранения
Слайд 15Волны Римана
- собственное значение матрицы
Определение. Простой волной (волной Римана) называется частное
решение
вида
вида
Характеристики семейства k – прямые линии
Слайд 16Волны Римана
- правый собственный вектор, соответствующий с.з.
Возможные случаи:
в этом случае
характеристики семейства k
называют истинно нелинейными
называют истинно нелинейными
1.
2.
характеристики семейства k
называют слабо нелинейными
x
t
x
t
формирование разрыва
при гладких начальных
данных разрыв не формируется
Слайд 17 Показать, что скалярное произведение
невырожденной замены переменных
инвариантно относительно
Показать, что семейство характеристик уравнений газовой динамики,
соответствующих собственному значению , является слабо нелинейным
Для одномерных уравнений
газовой динамики:
Консервативные переменные
Дифференциалы локальных характеристических переменных
Слайд 18Математические вопросы численного решения гиперболических систем уравнений
8. Классическое и
обобщенное решение гиперболической квазилинейной системы уравнений 1 порядка. Соотношения на сильном разрыве.
9. Пример неединственности обобщенного решения.
10. Энтропийные решения.
11. Условие эволюционности разрыва Лакса
12. Задача Римана о распаде произвольного разрыва. Точное решение задачи Римана о распаде произвольного разрыва
для линейной системы уравнений
9. Пример неединственности обобщенного решения.
10. Энтропийные решения.
11. Условие эволюционности разрыва Лакса
12. Задача Римана о распаде произвольного разрыва. Точное решение задачи Римана о распаде произвольного разрыва
для линейной системы уравнений
Слайд 19Вектор функция U называется классическим решением краевой задачи для
системы уравнений,
если
U и F непрерывно-дифференцируемые функции своих аргументов и
удовлетворяет краевым условиям и д.у. в области интегрирования поточечно.
Проблема существования классического решения
Необходимость обобщения классического решения введением разрывов
Проблема неединственности обобщенного решения
Допустимые разрывы. Критерии отбора допустимых разрывов
Устойчивость сильных разрывов. Условие Лакса
Метод исчезающей вязкости. Критерий Олейник/Лю (T.P.Liu)
Ударная адиабата
удовлетворяет краевым условиям и д.у. в области интегрирования поточечно.
Проблема существования классического решения
Необходимость обобщения классического решения введением разрывов
Проблема неединственности обобщенного решения
Допустимые разрывы. Критерии отбора допустимых разрывов
Устойчивость сильных разрывов. Условие Лакса
Метод исчезающей вязкости. Критерий Олейник/Лю (T.P.Liu)
Ударная адиабата
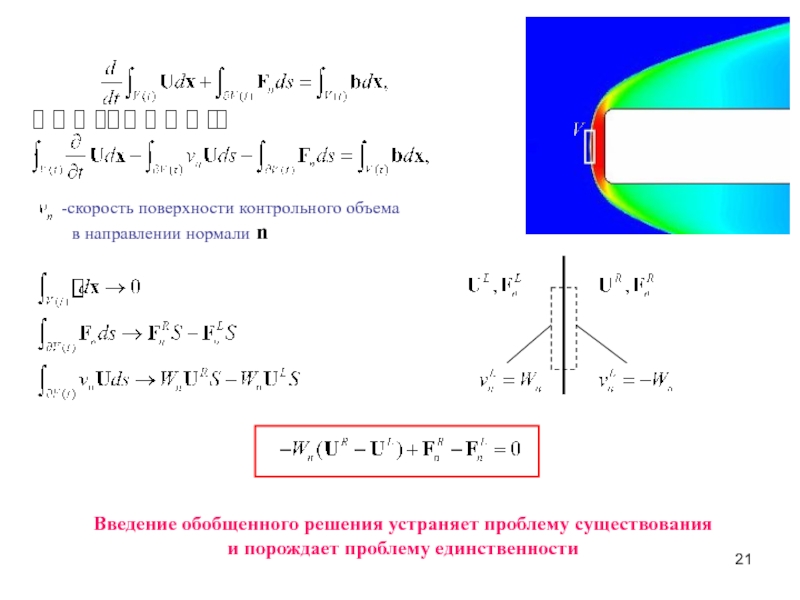
Слайд 21скорость поверхности контрольного объема
в направлении нормали n
Введение обобщенного решения
устраняет проблему существования
и порождает проблему единственности
и порождает проблему единственности
Слайд 22
В СК, связанной с разрывом Wn=0
Уравнения Эйлера
Уравнения релятивистской гидродинамики (СТО)
(1),
(2) =>
(4)
(3), (4) =>
Скорость разрыва отн. среды
(5)
Ударная адиабата Гюгонио
(1), (2) =>
обобщенный объем
Подставляем в
(4)
Ударная адиабата Тауба
симметрично
симметрично
После подстановки и в (1), получим
Слайд 23
Уравнения Эйлера
Уравнения релятивистской гидродинамики (СТО)
(4)
Скорость разрыва отн. среды
(5)
Ударная адиабата Гюгонио
Ударная адиабата Тауба
Перейдем к пределу в (4) и (5)
Скорость звука
Сохранение энтропии в пределе
беконечно малой интенсивности разрыва
Скорость звука в релятивистской
гидродинамике
Принцип причинности =>
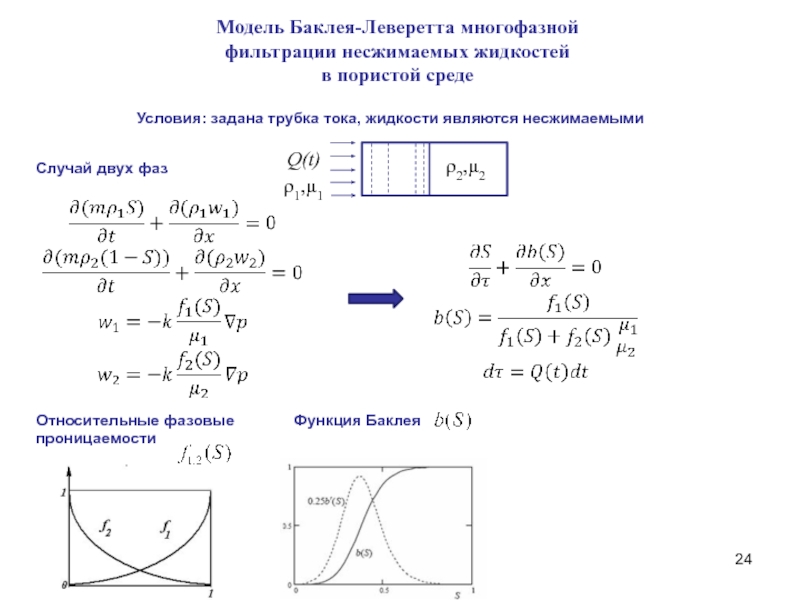
Слайд 24Модель Баклея-Леверетта многофазной
фильтрации несжимаемых жидкостей
в пористой среде
Относительные фазовые
проницаемости
Условия: задана трубка тока, жидкости являются несжимаемыми
Функция Баклея
Q(t)
ρ2,μ2
ρ1,μ1
Случай двух фаз
Слайд 25В задаче Баклея-Леверетта отношение вязкости вытесняемой жидкости
к вязкости вытесняющей – μ,
относительные фазовые проницаемости
пропорциональны квадратам фазовых насыщенностей.
Используя соотношение на разрыве, определить скорость распространения фронта вытеснения, значение насыщенности
за скачком.
пропорциональны квадратам фазовых насыщенностей.
Используя соотношение на разрыве, определить скорость распространения фронта вытеснения, значение насыщенности
за скачком.
Слайд 27Энтропийное решение
потребуем дополнительно
- поток энтропии
Случай кусочно-гладких решений
Условие устойчивости
(допустимости разрыва)
-необходимое и достаточное условие
существования вязкой структуры разрыва
возрастание энтропии
Слайд 28x
t
q
r
Условие эволюционности разрыва (P.Lax):
q+r+1=n
Лаксовский p-скачок:
*
Условия устойчивости Лакса
Слайд 29Метод малой вязкости
Скалярный пример
(Теорема Олейник)
Условие устойчивости разрыва имеет вид
при S1>S0
при S1
при S1
Условие Олейник
Условие Лакса
Прямая, соединяюшая точки (S0,b(S0)) и (S1,b(S1)) лежит
выше (ниже) графика зависимости b(S), соответственно
(обратное
неверно!)
Слайд 300
1
2
3
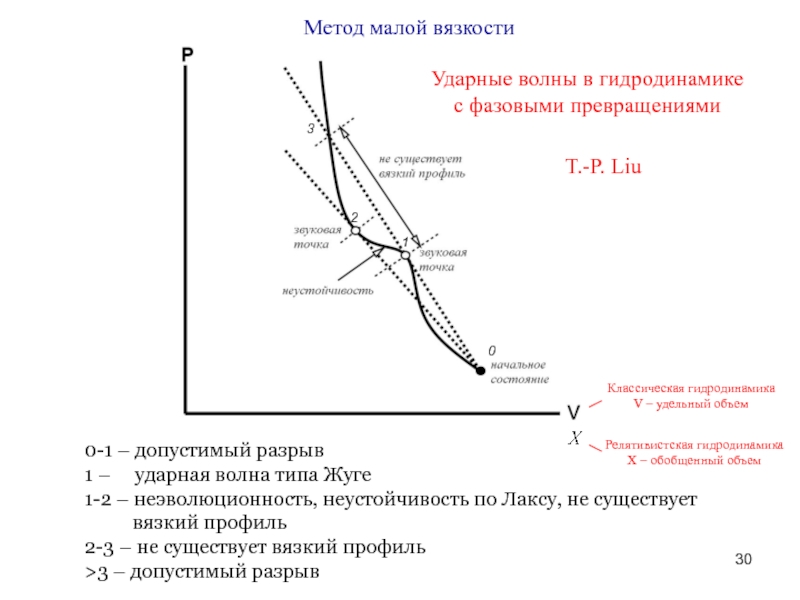
Ударные волны в гидродинамике с фазовыми превращениями
Метод малой вязкости
0-1 – допустимый
разрыв
1 – ударная волна типа Жуге
1-2 – неэволюционность, неустойчивость по Лаксу, не существует
вязкий профиль
2-3 – не существует вязкий профиль
>3 – допустимый разрыв
1 – ударная волна типа Жуге
1-2 – неэволюционность, неустойчивость по Лаксу, не существует
вязкий профиль
2-3 – не существует вязкий профиль
>3 – допустимый разрыв
Классическая гидродинамика
V – удельный объем
Релятивистская гидродинамика
X – обобщенный объем
T.-P. Liu
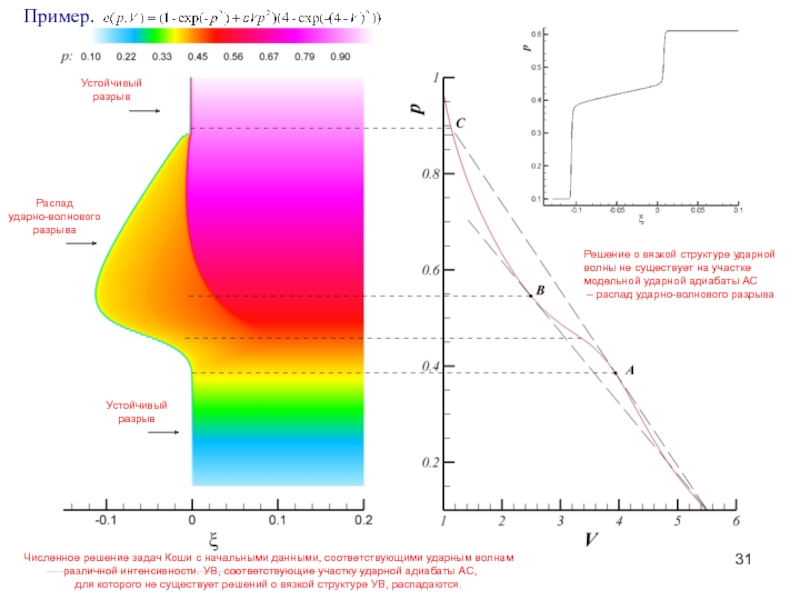
Слайд 31Решение о вязкой структуре ударной
волны не существует на участке
модельной ударной
адиабаты AC
– распад ударно-волнового разрыва
– распад ударно-волнового разрыва
Пример.
Численное решение задач Коши с начальными данными, соответствующими ударным волнам
различной интенсивности. УВ, соответствующие участку ударной адиабаты АС,
для которого не существует решений о вязкой структуре УВ, распадаются.
Распад
ударно-волнового
разрыва
Устойчивый
разрыв
Устойчивый
разрыв
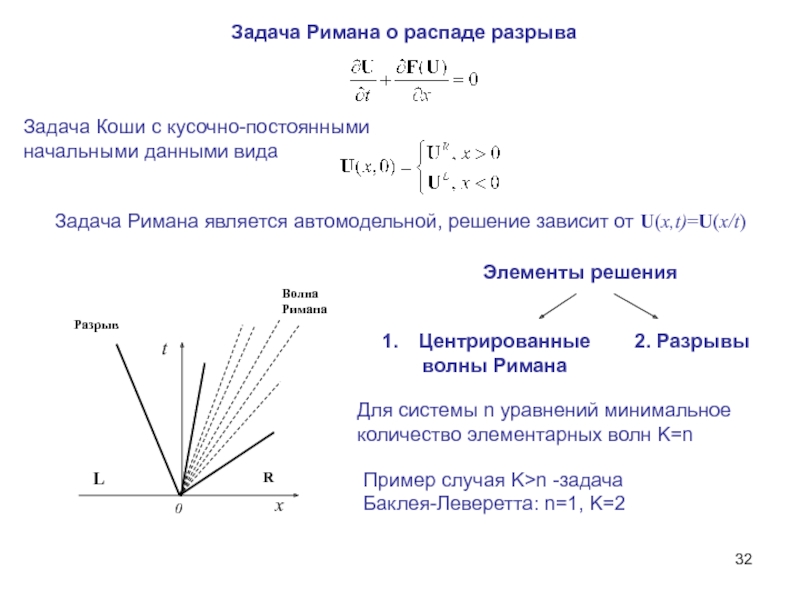
Слайд 32Задача Римана о распаде разрыва
Задача Коши с кусочно-постоянными
начальными данными вида
Задача
Римана является автомодельной, решение зависит от U(x,t)=U(x/t)
Элементы решения
Центрированные
волны Римана
2. Разрывы
R
L
Волна Римана
Разрыв
t
x
Для системы n уравнений минимальное
количество элементарных волн K=n
Пример случая K>n -задача
Баклея-Леверетта: n=1, K=2
0
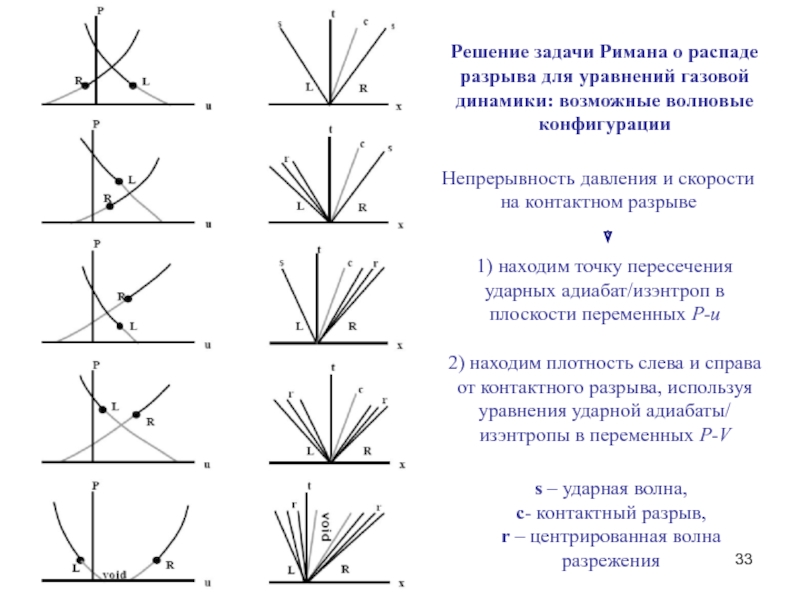
Слайд 33Решение задачи Римана о распаде разрыва для уравнений газовой динамики: возможные
волновые конфигурации
Непрерывность давления и скорости на контактном разрыве
1) находим точку пересечения
ударных адиабат/изэнтроп в
плоскости переменных P-u
2) находим плотность слева и справа от контактного разрыва, используя уравнения ударной адиабаты/ изэнтропы в переменных P-V
s – ударная волна,
c- контактный разрыв,
r – центрированная волна разрежения
Слайд 34Точное решение задачи Римана о распаде произвольного разрыва
для линейной системы уравнений
K=n
Элемент k –”ступенька” для инварианта Римана k
Решение для вектора U=R-1w
Решение для вектора потоков F=AU
при ξ=0 (для интегрирования уравнений на стационарных сетках)
Слайд 35Решение задачи Римана в скалярном случае
1.Точное решение для произвольного потока f(u)
2.Частный
случай потока, имеющего единственный минимум в точке ω и не имеющего локальных максимумов
3.Монотонный поток f(u)
(разность ‘против потока’)
3.Монотонный поток f(u)
(разность ‘против потока’)
Слайд 36Математические вопросы численного решения гиперболических систем уравнений
13. Численный метод
Годунова.
Слайд 37Численный метод Годунова (1D)
1. Консервативная аппроксимация
t
x
2. Определение потоков через
границу ячейки из точного решения задачи о распаде разрыва
решение задачи о распаде разрыва в точке xj+1/2 c кусочно-постоянными начальными данными
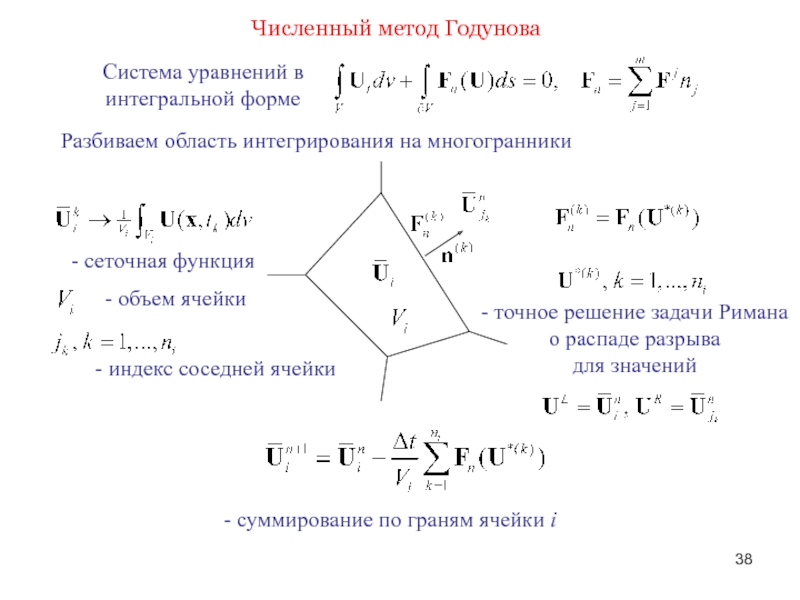
Слайд 38Численный метод Годунова
Система уравнений в
интегральной форме
Разбиваем область интегрирования
на многогранники
- точное решение задачи Римана
о распаде разрыва
для значений
- сеточная функция
- суммирование по граням ячейки i
- объем ячейки
- индекс соседней ячейки
Слайд 39В случае декартовой СК (x,y) и равномерной сетки
В случае декартовой
СК (x,y) и равномерной сетки
i, j
i+1/2,j
В одномерном случае
Проекции вектора нормали к граням ячейки
Объем ячейки
i,j+1/2
Слайд 40Метод Годунова для линейной гиперболической
системы уравнений:
Для определения потоков на гранях
используется точное решение задачи Римана о распаде произвольного разрыва:
Консервативная аппроксимация имеет вид
матрица правых собственных
векторов матрицы
Слайд 41Эквивалентная запись схемы в терминах потоков
схема Годунова для линейной системы уравнений
эквивалентна применению схемы “разность против потока” первого порядка при аппроксимации уравнений переноса для инвариантов Римана.
и в терминах инвариантов Римана линейной системы
Слайд 42Свойства схемы первого порядка “разность против потока”
(условие Куранта, Фридрихса,
Леви)
Положительность:
Из положительности следует монотонность схемы:
Устойчивость:
Слайд 45Математические вопросы численного решения гиперболических систем уравнений
14. Приближенные решения
задачи о распаде разрыва: Метод Роу,
метод Хартена-Лакса-Ван Лира (HLL), метод HLLC, схемы Лакса Фридрихса и Русанова.
15.Многомерная неустойчивость численных решений. Карбункул-эффект. Тесты Квирка.
16. Гибридные приближенные методы: Roe-HLL, Roe- Rusanov
метод Хартена-Лакса-Ван Лира (HLL), метод HLLC, схемы Лакса Фридрихса и Русанова.
15.Многомерная неустойчивость численных решений. Карбункул-эффект. Тесты Квирка.
16. Гибридные приближенные методы: Roe-HLL, Roe- Rusanov
Слайд 46Метод Роу
Требования к матрице A(UL,UR)
1. Гиперболичность
2. Соответствие точной матрице Якоби
3.
Для произвольных UL и UR имеет место равенство
параметрический вектор от которого F и U
зависят квадратично
Приближенные методы решения задачи о распаде разрыва
(упрощение волновой структуры и априорные оценки скоростей разрывов)
Вместо точного решения задачи о распаде разрыва с кусочно-постоянными начальными данными для нелинейной системы рассматривается решение задачи для линеаризованной системы с некоторой матрицей A(UL,UR)
Способ линеаризации
Roe P. L., Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes,
J.Comput.Physics, 43, N2, 1981, 357-372.
Слайд 48Свойство метода Роу. Пусть левые и правые величины UL и UR
связаны
соотношениями на разрыве
соотношениями на разрыве
W – скорость распространения разрыва. Тогда W – собственное
значение, осредненной по Роу матрицы A.
■
– собственный вектор матрицы A,
соответствующий собственному значению W.
Слайд 49Поток пропорциональный
градиенту решения
Энтропийная коррекция Хартена
При использовании линеаризации по Роу соотношения на
стационарном
разрыве выполнены точно (как для волны сжатия так и для волны разрежения!).
разрыве выполнены точно (как для волны сжатия так и для волны разрежения!).
Отбор решений ? Энтропийная коррекция
Потребуем положительную определенность матрицы
диссипативных коэффициентов (нарушается в звуковых точках)
Слайд 50
Обобщение на произвольное уравнение состояния. Метод Глэйстера.
Glaister P., An Approximate Linearized
Riemann Solver for the Euler Equations for Real Gases.,
Journal of Comput. Physics, 74, 1988, 382-408.
Mottura L., Vigevano L., and Zaccanti M., An Evaluation of Roe’s Scheme Generalizations
for Equlibrium Real Gas Flows, Journal of Comput. Physics, 138-354-399, 1997
Journal of Comput. Physics, 74, 1988, 382-408.
Mottura L., Vigevano L., and Zaccanti M., An Evaluation of Roe’s Scheme Generalizations
for Equlibrium Real Gas Flows, Journal of Comput. Physics, 138-354-399, 1997
Обобщение на различные гиперболические системы уравнений
Недостатки: неединственность, необходимость энтропийной коррекции
система уравнений идеальной магнитной гидродинамики,
системы уравнений релятивистской гидродинамики (СТО и ОТО),
…
Слайд 51Метод Хартена-Лакса-ван Лира (HLL)
x
t
dx/dt=SL
dx/dt=SR
UL
UR
U*
Требуется оценка
скоростей SL и SR!
Слайд 52Метод HLLC (C for contact)
Toro et al. 1994
x
t
dx/dt=SL
dx/dt=SR
UL
UR
U*L
U*R
dx/dt=S*
+ условия на контактном
разрыве:
Слайд 53Метод HLLC (C for contact)
Toro et al. 1994
x
t
SLt
SRt
UL
UR
U*L
U*R
S*t
Требуется оценка
скоростей SL, SR,
S*
Слайд 54Оценки скоростей
1.
2.
Оценка с использованием собственных значений осредненной по Роу
матрицы Якоби
Слайд 55Схема Русанова
1. В методе КИР
заменим собственные значения оценкой спектрального радиуса
матрицы
Якоби
Якоби
2. В потоке Хартена-Лакса-ван Лира
оценим скорости волн
cхема Хартена-Лакса-ван Лира перейдет в схему Русанова
Оценка для S+
Слайд 56Схема Лакса-Фридрихса
Если в схеме Русанова
положить
получим поток в схеме Лакса-Фридрихса
Дополнительная литература
Слайд 59Точное решение задачи Римана
о распаде разрыва
2. Метод Роу
(решение задачи
о распаде разрыва для линеаризованной системы)
3. Метод HLLC
4. Meтод HLL
5. Метод Русанова
6. FORCE
7. Метод Лакса-Фридрихса
о распаде разрыва для линеаризованной системы)
3. Метод HLLC
4. Meтод HLL
5. Метод Русанова
6. FORCE
7. Метод Лакса-Фридрихса
Вычисление потока через границу ячейки
F(UL,UR):
Точность
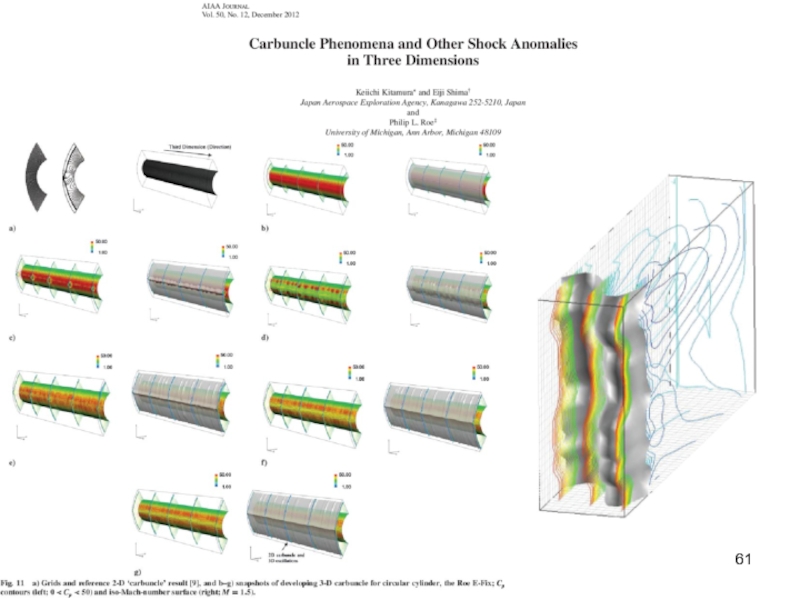
Карбункул-эффект. Гибридные вращательные методы
решения задачи Римана (Nishikava, Kitamura, 2008).
Методы, учитывающие контактный разрыв, подвержены численной
Неустойчивости “карбункул-эффект”
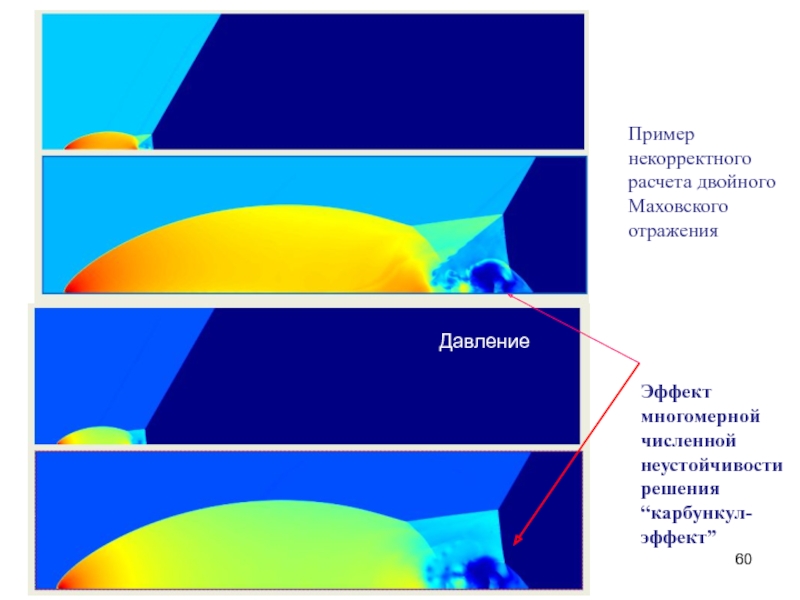
Слайд 60Пример некорректного
расчета двойного
Маховского отражения
Давление
Эффект
многомерной
численной
неустойчивости
решения
“карбункул-эффект”
Слайд 64Шаг интегрирования по времени
Метод Рунге-Кутта второго порядка точности
Схема TVD
с ограничителем van
Albada
Слайд 65При построении вращательного гибридного метода комбинируются
различные способы приближенного решения задачи о
распаде разрыва
Метод Роу
Слайд 67Энтропийная коррекция
Амплитуды волн
Метод HLL
В качестве скоростей волн
используются минимальное и максимальное собственное
значение
Слайд 74Дополнительная литература
Nishikawa, H.; Kitamura, K. (2008), "Very simple, carbuncle-free, boundary-layer-resolving,
rotated-hybrid Riemann solvers", J. Comput. Phys. 227 (4): 2560–2581
Слайд 75Некоторые вопросы численного интегрирования систем уравнений гиперболического типа
Схемы TVD
(Total variation
diminishing)
17. Свойство TVD. Принцип построения TVD схем второго порядка
аппроксимации. Теорема Хартена о достаточном условии.
18. Семейство противопоточных TVD схем второго порядка аппроксимации.
Функции ограничители. Диаграмма Sweby.
19. Применение к квазилинейным гиперболическим системам уравнений.
TVD cхема Хартена. Ограничители наклонов. TVD cхемы типа MUSCL
Слайд 76Схемы TVD (total variation diminishing)
Монотонные схемы.
Не существует монотонных линейных схем
с
порядком аппроксимации выше первого. (Годунов С.К.)
порядком аппроксимации выше первого. (Годунов С.К.)
Теорема Годунова не распространяется на нелинейные схемы (шаблон и
аппроксимация зависят от решения)
Свойство TVD. Принцип построения TVD схем второго порядка
аппроксимации. Теорема Хартена (о достаточном условии).
Семейство противопоточных TVD схем второго порядка аппроксимации.
Функции ограничители. Диаграмма Sweby.
Применение к квазилинейным системам уравнений.
Ограничители наклонов. Схемы типа MUSCL
Слайд 77Схемы TVD (total variation diminishing)
Теорема (Harten, 1982). Если схема записывается в
виде
и выполнены условия
то данная схема является схемой TVD.
TVD- свойство:
где
- полная вариация решения
Слайд 78Схемы TVD (total variation diminishing)
-
все коэффициенты положительны
Суммируем по i от
до
(замена индексов)
Рассматривается разность уравнений в соседних узлах:
Теорема Хартена
Слайд 79Схемы TVD (total variation diminishing)
Основная идея: представить поток в виде суммы
потока монотонной схемы
первого порядка аппроксимации и ограниченного антидиффузионного потока
первого порядка аппроксимации и ограниченного антидиффузионного потока
Условие на функцию
достаточное для того, чтобы схема обладала
свойством TVD, получаем с использованием теоремы Хартена
Противопоточная схема 1-го порядка аппроксимации – схема TVD
Схема TVD высокого порядка
Схема TVD низкого порядка
Функция ограничитель
Поток схемы высокого порядка
Схема имеет второй порядок аппроксимации, если
Действительно,
Слайд 80Схемы TVD (total variation diminishing)
Линейное уравнение
Поток, соответствующий схеме второго порядка
Домножим антидиффузионный
член на функцию ограничитель
Схема неустойчива!
Теорема Хартена
(достаточное условие TVD)
Подстановка в уравнение
антидиффузионный
поток
Схема 1го порядка
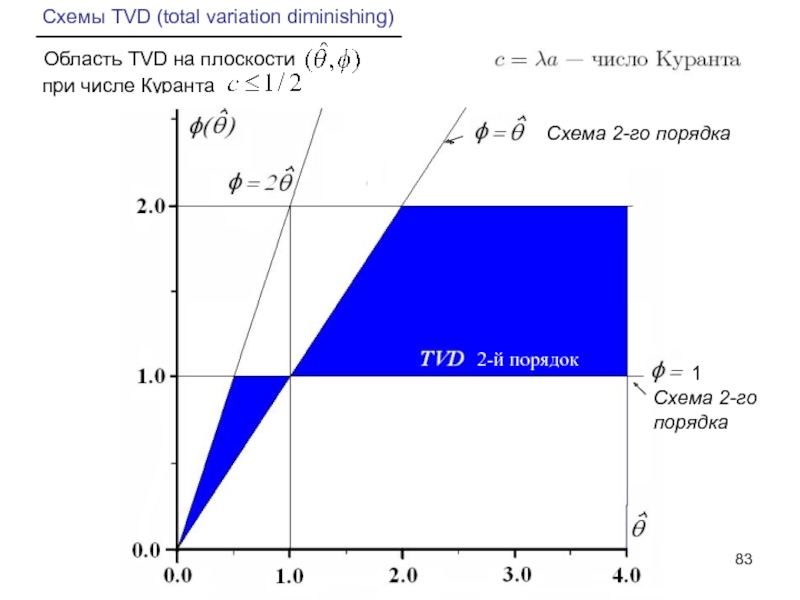
Слайд 83Схемы TVD (total variation diminishing)
Область TVD на плоскости
при числе Куранта
1
Схема
2-го порядка
Схема 2-го
порядка
2-й порядок
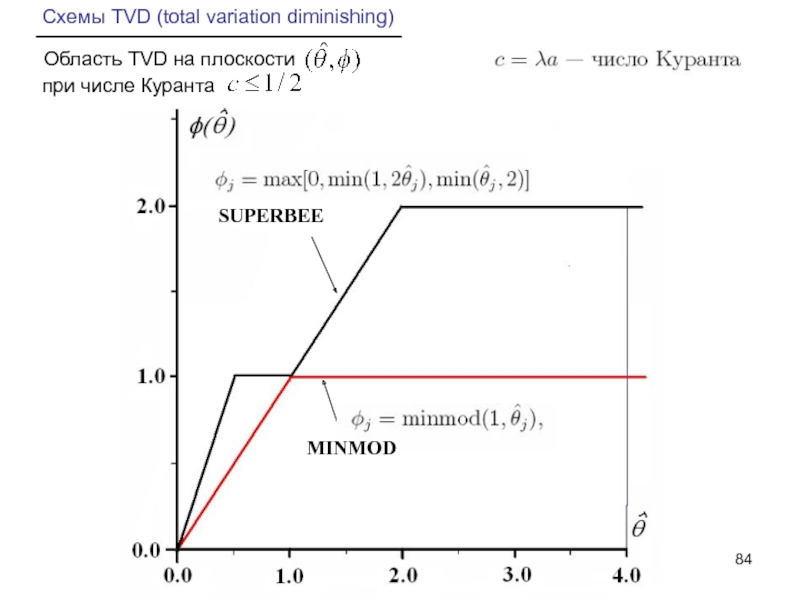
Слайд 84Схемы TVD (total variation diminishing)
Область TVD на плоскости
при числе Куранта
SUPERBEE
MINMOD
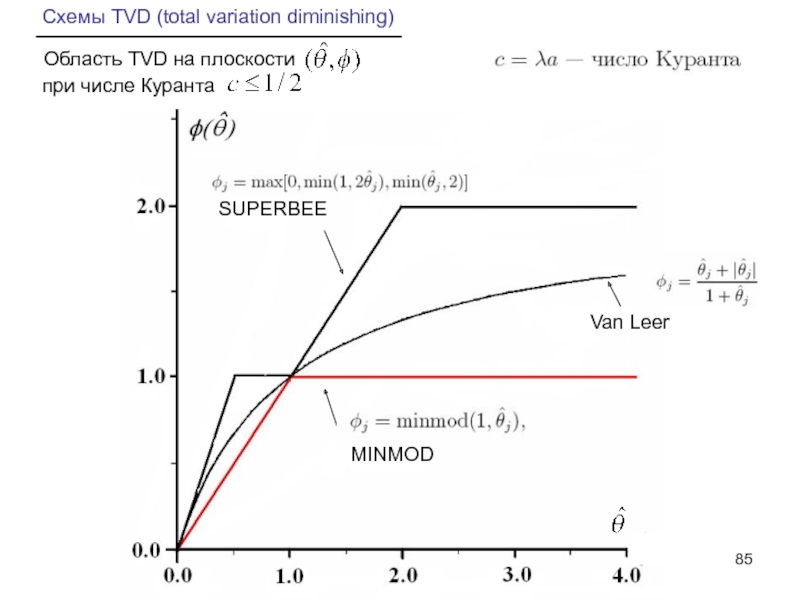
Слайд 85Схемы TVD (total variation diminishing)
Область TVD на плоскости
при числе Куранта
SUPERBEE
MINMOD
Van
Leer
Слайд 88Схемы TVD (total variation diminishing)
20. Ограничители наклонов. Схемы TVD типа MUSCL.
Применение к гиперболическим системам уравнений
Схемы TVD
(продолжение)
21. Интегрирование по времени: методы Рунге-Кутта, сохраняющие
свойство TVD
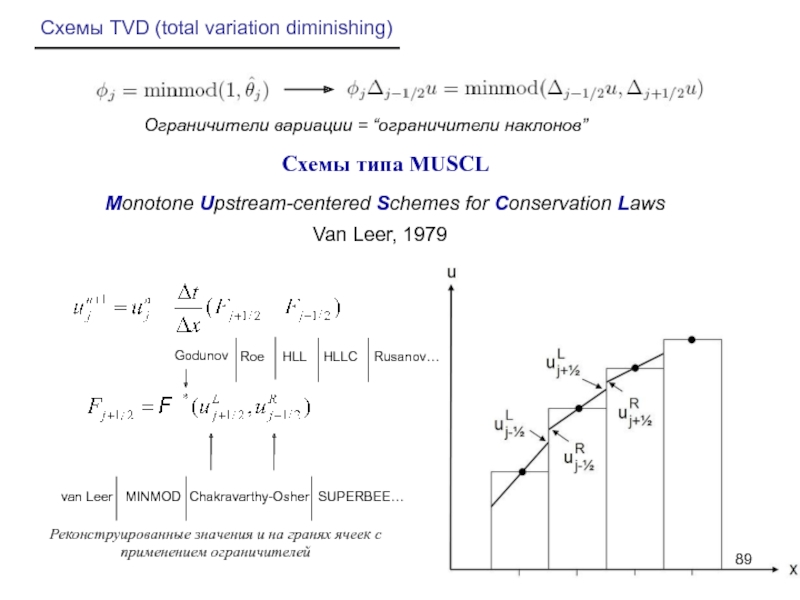
Слайд 89Схемы TVD (total variation diminishing)
Ограничители вариации = “ограничители наклонов”
Cхемы типа MUSCL
Monotone
Upstream-centered Schemes for Conservation Laws
Van Leer, 1979
Roe
Godunov
HLL
HLLC
Rusanov…
Реконструированные значения u на гранях ячеек с применением ограничителей
van Leer MINMOD Chakravarthy-Osher SUPERBEE…
Слайд 90Схемы TVD (total variation diminishing)
Кусочно-постоянное распределение – 1й порядок аппроксимации
Кусочно-линейное распределение
– 2й порядок аппроксимации
Пример. Показать, что схема Годунова для уравнения
с линейной реконструкцией (*) является схемой TVD
(*)
Схема TVD при
Слайд 91Схемы TVD (total variation diminishing)
Применение к системам гиперболических уравнений
Шаг 1: реконструкция
с использованием консервативных переменных)
Шаг 2: решение задачи о распаде разрыва
Шаг 2: интегрирование по времени
Примечание. Требуется энтропийная коррекция:
Слайд 95Пусть
- схема TVD 1-го порядка по t
Схемы TVD (total variation diminishing)
Методы Рунге-Кутта для системы ОДУ
Теорема (Shu,Osher)
Схема * является схемой TVD при условии
если коэффициенты неотрицательны
*
при
Слайд 96
Интегрирование по времени. Метод Рунге-Кутта (TVD - 3) (с=1).
Интегрирование по времени.
Метод Рунге-Кутта (TVD - 2) (с=1).
Оптимальные методы доставляют максимум параметру c:
Схемы TVD
Метод Рунге-Кутта 4-го порядка с неотрицательными весами построить нельзя!
Слайд 97Пример. Если схема
является схемой TVD,
схема второго порядка точности
также является схемой TVD
схема второго порядка точности
также является схемой TVD
Схемы TVD
Согласно условию
Слайд 98Схемы TVD (total variation diminishing)
Пример.
TVD схема первого порядка для
уравнения Хопфа:
Задача Коши
TVD
реконструкция
Решение задачи о
распаде разрыва
Слайд 99Схемы TVD (total variation diminishing)
Сравнение двух методов Рунге-Кутта
1 TVD
2 не TVD
Схема TVD при условии
отрицательные коэффициенты
Интегрирование с шагом
Слайд 102Некоторые вопросы численного интегрирования систем уравнений гиперболического типа
Схемы ENO
(Essentially non-oscillatory
schemes)
22. Полиномиальная реконструкция в расчетных ячейках.
Концепция адаптивного шаблона. ENO алгоритм.
Свойства ENO реконструкции.
23. ENO схемы в многомерном случае.
Слайд 103A.Harten, B. Engquist, S.Osher and S. Chakravarthy, Uniformly high order
essentially
non-oscillatory schemes, III, Journal of Computational Physics,
v.71 (1987), pp. 231-303.
G.-S. Jiang and C.-W. Shu, Efficient Implementation of Weighted ENO Schemes, Journal of Computational Physics, v.126 (1996), pp. 202-228.
Chi-Wang Shu, Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws. ICASE report 97-65, 1997
v.71 (1987), pp. 231-303.
G.-S. Jiang and C.-W. Shu, Efficient Implementation of Weighted ENO Schemes, Journal of Computational Physics, v.126 (1996), pp. 202-228.
Chi-Wang Shu, Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws. ICASE report 97-65, 1997
Литература
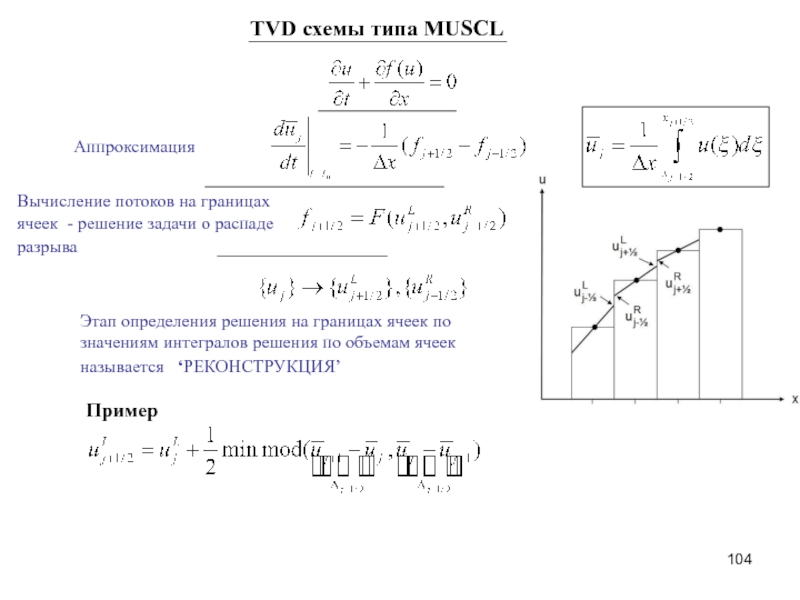
Слайд 104TVD схемы типа MUSCL
Аппроксимация
Вычисление потоков на границах ячеек - решение
задачи о распаде разрыва
Этап определения решения на границах ячеек по значениям интегралов решения по объемам ячеек называется ‘РЕКОНСТРУКЦИЯ’
Пример
Слайд 105TVD схемы типа MUSCL
Аппроксимация
Вычисление потоков на границах ячеек - решение
задачи о распаде разрыва
Этап определения решения на границах ячеек по значениям интегралов решения по объемам ячеек называется ‘РЕКОНСТРУКЦИЯ’
Схемы ТVD - Ограничение наклонов - Обязательное переключение на схему первого порядка вблизи экстремумов
Нет смысла строить TVD схемы очень высокого порядка (>2,3) т.к. качество решения ограничивается переходом на первый порядок
=> Схемы ENO – реконструкция на адаптивном шаблоне - произвольно высокий порядок в области гладкости в том числе вблизи экстремумов
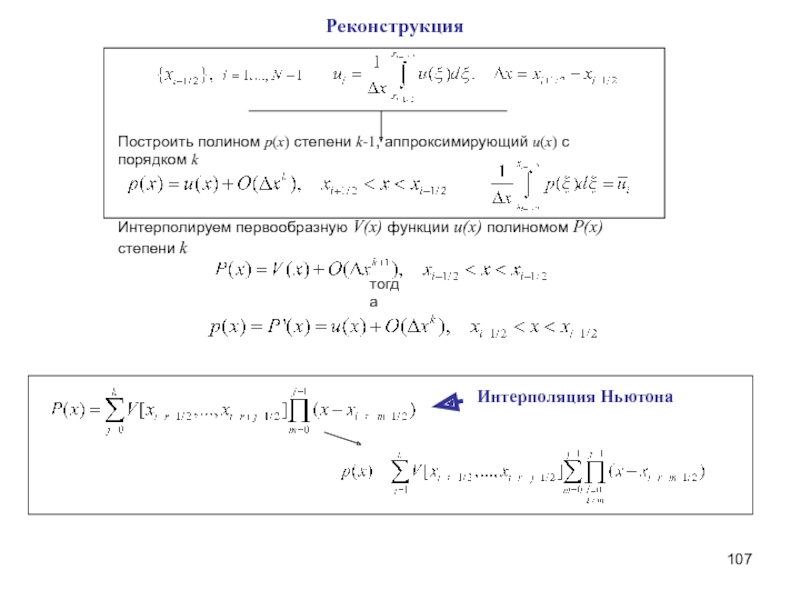
Слайд 106Построить полином p(x) степени k-1, аппроксимирующий u(x) с порядком k
Интерполируем первообразную
V(x) функции u(x) полиномом P(x) степени k
тогда
A.Harten, B. Engquist, S.Osher and S. Chakravarthy, Uniformly high order
essentially non-oscillatory schemes, III, Journal of Computational Physics,
v.71 (1987), pp. 231-303.
Реконструкция
Слайд 107Построить полином p(x) степени k-1, аппроксимирующий u(x) с порядком k
Интерполируем первообразную
V(x) функции u(x) полиномом P(x) степени k
тогда
Реконструкция
Интерполяция Ньютона
Слайд 110такой, что разность потоков аппроксимирует производную
с порядком k
По значениям функции
в точках
Связь реконструкции с конечноразностными консервативными схемами
в узлах сетки
Поток в узлах сетки
Поток на границах ячеек
найти разностный поток
(Shu, Osher)
Реконструкция
Слайд 111Идея метода ENO:
Для увеличения порядка интерполяционного полинома по возможности привлекаются данные
из области гладкости решения
(шаблон адаптируется к решению)
Задача. Найти шаблон k+1 последовательных точек включающий i-1/2 и i+1/2 такой, что V(x) является “наиболее гладкой” на этом шаблоне по сравнению c другими возможными шаблонами
Решение.
шаг 1
(шаблон адаптируется к решению)
Задача. Найти шаблон k+1 последовательных точек включающий i-1/2 и i+1/2 такой, что V(x) является “наиболее гладкой” на этом шаблоне по сравнению c другими возможными шаблонами
Решение.
шаг 1
шаг 2
шаг k
Слайд 112
Реконструкция решения на гранях ячейки
Пример.
ENO схема выбирает один из шаблонов, тот
на котором решение
является наиболее гладким. Мерой гладкости являются абсолютные
величины разделенных разностей.
является наиболее гладким. Мерой гладкости являются абсолютные
величины разделенных разностей.
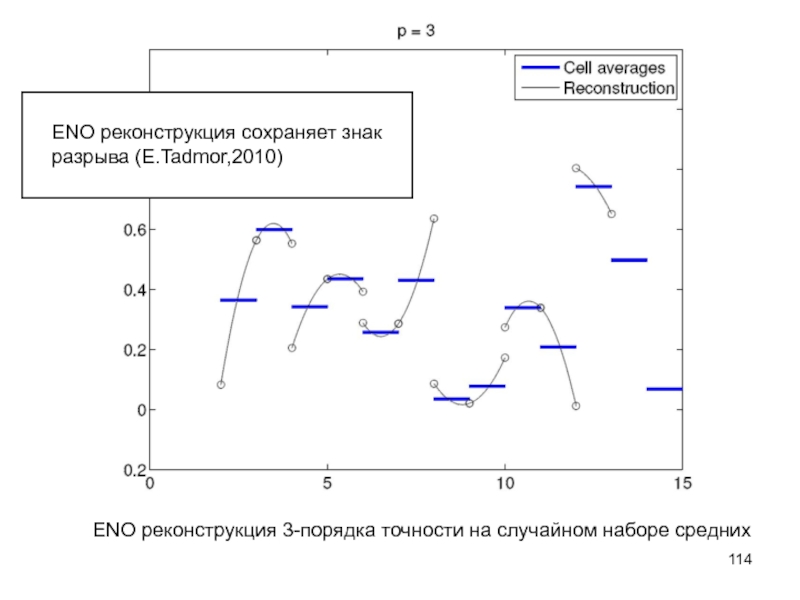
Слайд 114ENO реконструкция 3-порядка точности на случайном наборе средних
ENO реконструкция
сохраняет знак
разрыва (E.Tadmor,2010)
разрыва (E.Tadmor,2010)
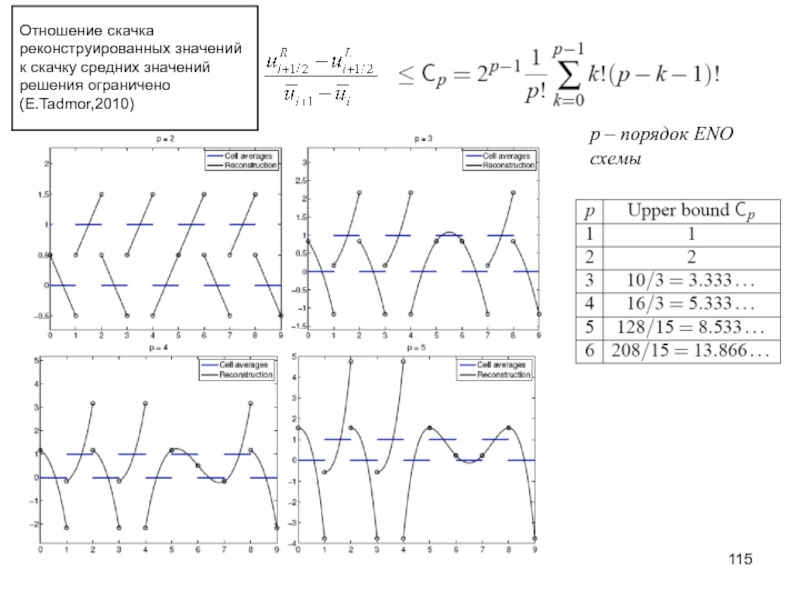
Слайд 115
p – порядок ENO
схемы
Отношение скачка реконструированных значений к скачку средних значений
решения ограничено (E.Tadmor,2010)
Слайд 116Некоторые вопросы численного интегрирования систем уравнений гиперболического типа
Схемы WENO
(Weighted essentially
non-oscillatory schemes)
24. Концепция WENO схем. Индикаторы гладкости решения.
Свойства WENO реконструкции.
Слайд 117Возможности для совершенствования схем ENO
1. Шаблон может изменяться из-за малых
ошибок в областях с нулевыми производными решения. В областях гладкости решения эта случайная адаптация нежелательна.
2. Возможны проблемы со сходимостью.
3. В процессе выбора шаблона рассматриваются k конкурирующих шаблонов включающих 2k-1 ячеек, из них только один используется для реконструкции решения на гранях ячеек с порядком аппроксимации k. Если бы использовались все 2k-1 ячеек, то можно было бы получить порядок аппроксимации 2k-1.
4. ENO процедура выбора шаблона использует большое количество логических операций.
Развитие этих возможностей – схемы WENO
2. Возможны проблемы со сходимостью.
3. В процессе выбора шаблона рассматриваются k конкурирующих шаблонов включающих 2k-1 ячеек, из них только один используется для реконструкции решения на гранях ячеек с порядком аппроксимации k. Если бы использовались все 2k-1 ячеек, то можно было бы получить порядок аппроксимации 2k-1.
4. ENO процедура выбора шаблона использует большое количество логических операций.
Развитие этих возможностей – схемы WENO
X.-D. Liu, S. Osher and T.Chan, Weighted essentially nonoscillatory schemes,
Journal of Computational Physics, v.115 (1994), pp.200-212.
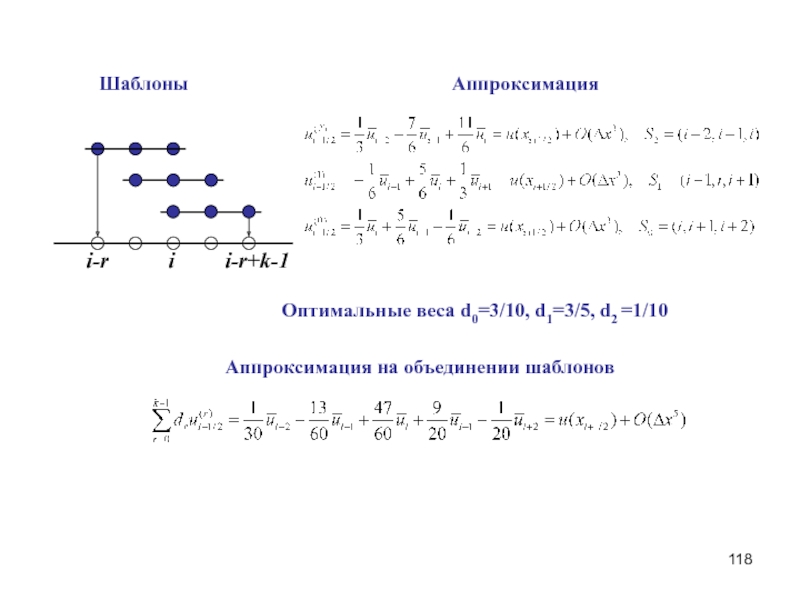
Слайд 118Шаблоны
i-r+k-1
i
i-r
Аппроксимация
Оптимальные веса d0=3/10, d1=3/5, d2 =1/10
Аппроксимация на объединении шаблонов
Слайд 119
Основная идея: вместо использования для реконструкции только одного из конкурирующих шаблонов
используется выпуклая комбинация всех. Вклад каждого шаблона регулируется индикаторами гладкости решения.
k реконструированных значений u на k шаблонах
WENO реконструкция
1.
(оптимальные веса):
k=1
k=2
k=3
Пусть в области гладкости
, тогда схема имеет порядок точности 2k-1
Действительно,
2.
Слайд 120Это приводит к следующему представлению для весов
На основе вычислительных экспериментов
в работе
получено выражение для индикаторов гладкости
G.Jiang and C.-W.Shu, Efficient implementation of weighted ENO schemes, Journal
Of Computational Physics, v.126 (1996), pp.202-228.
3. Если функция имеет разрывы на одном или нескольких шаблонах потребуем, чтобы соответствующие веса обращались в нуль эмулируя, концепцию ENO.
4. Веса должны быть гладкими функциями и вычислительно эффективными.
Слайд 121
G.Jiang and C.-W.Shu, Efficient implementation of weighted ENO schemes, Journal
Of
Computational Physics, v.126 (1996), pp.202-228.
Слайд 122
G.Jiang and C.-W.Shu, Efficient implementation of weighted ENO schemes, Journal
Of
Computational Physics, v.126 (1996), pp.202-228.
На шаблоне не содержащем разрыв
На шаблоне содержащем разрыв
решения
Веса, соответствующие шаблонам
содержащим разрывы
Шаблоны содержащие разрывы получают веса, стремящиеся к нулю при
Слайд 123WENO реконструкция
при k=3
1.Индикаторы гладкости
2. Веса
3.Реконструкция
- симметрично.
шаблоны
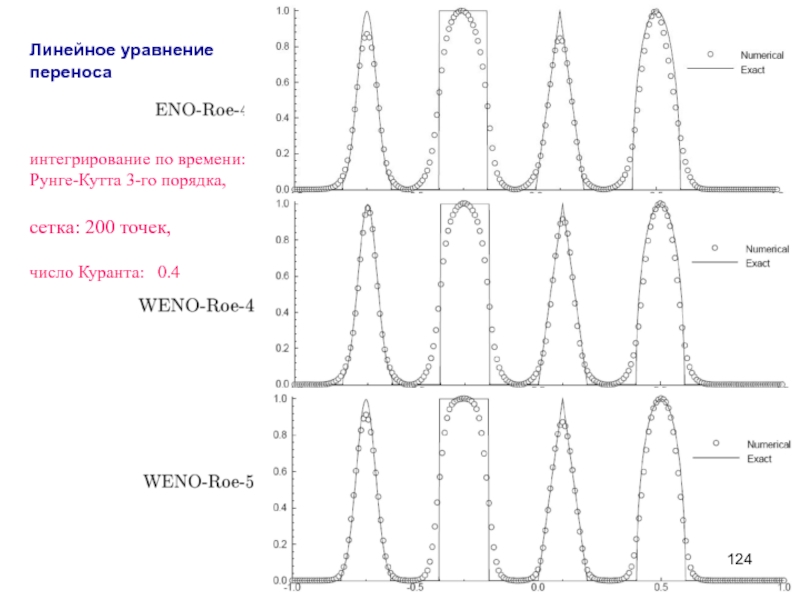
Слайд 124Линейное уравнение
переноса
интегрирование по времени:
Рунге-Кутта 3-го порядка,
сетка: 200 точек,
число Куранта: 0.4
Слайд 125Задача Баклея-Леверетта
интегрирование по времени:
Рунге-Кутта 3-го порядка,
сетка: 81, число Куранта: 0.4
Слайд 126Тест
“задача Сода”
Рунге-Кутта 3,
сетка: 101,
число Куранта: 0.6
Тест
“задача Лакса”
Рунге-Кутта 3,
сетка: 101,
число
Куранта: 0.6
Слайд 128Некоторые вопросы численного интегрирования систем уравнений гиперболического типа
25. Применение методики
локального
предобуславливания для гиперболических систем уравнений
предобуславливания для гиперболических систем уравнений
Слайд 131≤1 выбирается так, что
Параметр 0
собственные значения имеют один порядок величины.
Применение методики локального предобуславливания
при решении стационарных задач.
Спектр исходной
матрицы Якоби
После умножения
на предобуславливатель
Слайд 132
- увеличение шага интегрирования по времени
- улучшение сходимости
- повышение точности при
малых числах Маха
- улучшение сходимости
- большая ‘глубина’ сходимости
Применение методики локального предобуславливания
при решении стационарных задач.
Спектр исходной
матрицы
- предобуславливания нет
- число обусловленности ~1
Явная схема
Неявная схема
Эффект
Слайд 133
Применение предобуславливателя со схемами, использующими
решение задачи о распаде разрыва для линеаризованной
системы
уравнений.
уравнений.
стабилизирующий член
Введение предобуславливателя в решение задачи о распаде разрыва:
Слайд 134
S.V.Utyuzhnikov, A.V.Konyukhov, S.V.Vasil’evskii, D.V.Rudenko, S.A.Vasilievsky, A.F.Kolesnikov, O.Chazot
Simulation of Subsonic and
Supersonic Flows In Inductive Plasmatrons,
AIAA Journal, vol.42, N9, pp.1871-1877(7), 2004.
AIAA Journal, vol.42, N9, pp.1871-1877(7), 2004.
