и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует для данного момента, а уравнения будут существовать вечно» А. Эйнштейн.
Работу выполнил ученик 7»Г» класса МАОУ «Медико-биологический лицей» Артюхин Сергей
Руководитель Храмова С.В.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы уравнений и их графическое решение презентация
Содержание
- 1. Системы уравнений и их графическое решение
- 2. Цель: Выяснить, является ли графический способ
- 3. Системы уравнений и методы их решений. Системой
- 4. Программа, упрощающая решение систем уравнений графическим
- 5. Плюсы и минусы графического метода решения систем
- 6.
- 7.
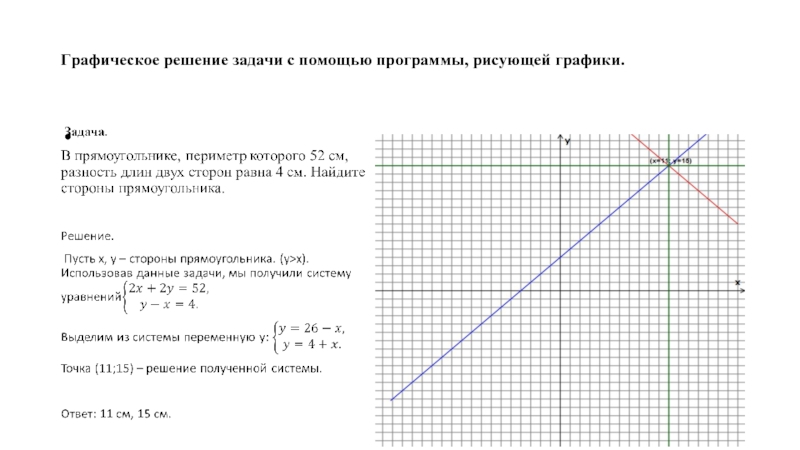
- 8. Графическое решение задачи с помощью программы, рисующей графики.
- 9. Заключение. В процессе работы я
Слайд 2
Цель: Выяснить, является ли графический способ самым рациональным для решения систем
уравнений.
Задачи исследования:
Рассмотреть различные аналитические и графический способы решения систем уравнений.
Научиться решать задачи с помощью систем уравнений.
Создать программу, помогающую упростить решение систем уравнений графическим способом.
Методы исследования:
Подумать самостоятельно;
Посмотреть книги;
Обратиться к компьютеру, посмотреть в глобальной сети Интернет;
Познакомиться с опытом других людей
Задачи исследования:
Рассмотреть различные аналитические и графический способы решения систем уравнений.
Научиться решать задачи с помощью систем уравнений.
Создать программу, помогающую упростить решение систем уравнений графическим способом.
Методы исследования:
Подумать самостоятельно;
Посмотреть книги;
Обратиться к компьютеру, посмотреть в глобальной сети Интернет;
Познакомиться с опытом других людей
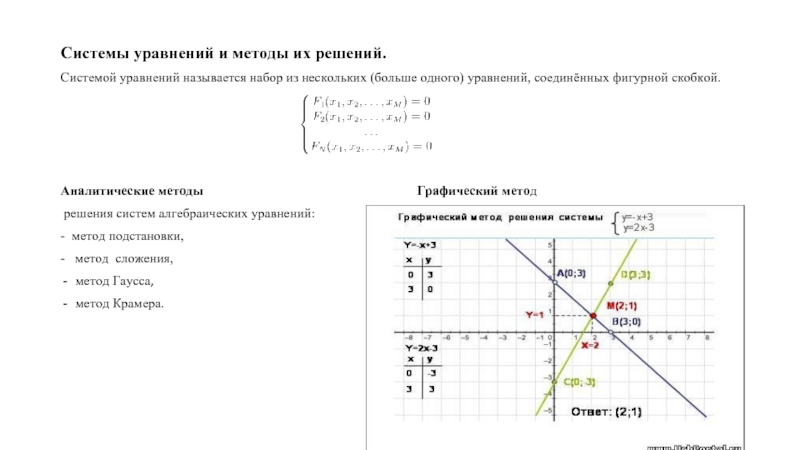
Слайд 3Системы уравнений и методы их решений.
Системой уравнений называется набор из нескольких
(больше одного) уравнений, соединённых фигурной скобкой.
Аналитические методы Графический метод
решения систем алгебраических уравнений:
- метод подстановки,
- метод сложения,
метод Гаусса,
метод Крамера.
Аналитические методы Графический метод
решения систем алгебраических уравнений:
- метод подстановки,
- метод сложения,
метод Гаусса,
метод Крамера.
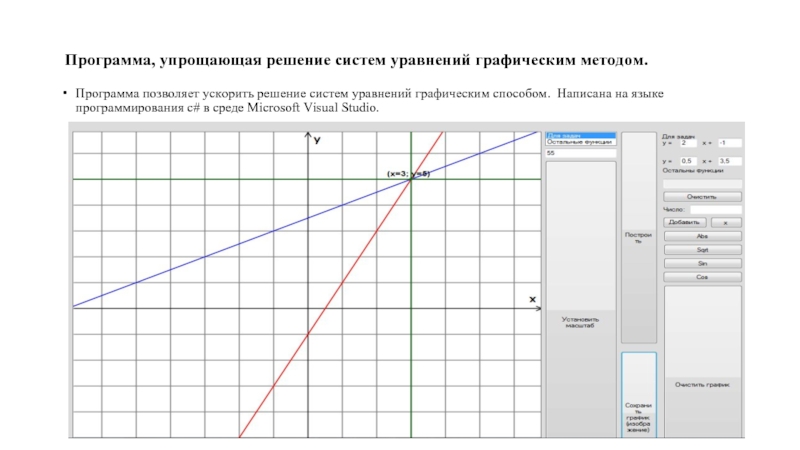
Слайд 4 Программа, упрощающая решение систем уравнений графическим методом.
Программа позволяет ускорить решение
систем уравнений графическим способом. Написана на языке программирования c# в среде Microsoft Visual Studio.
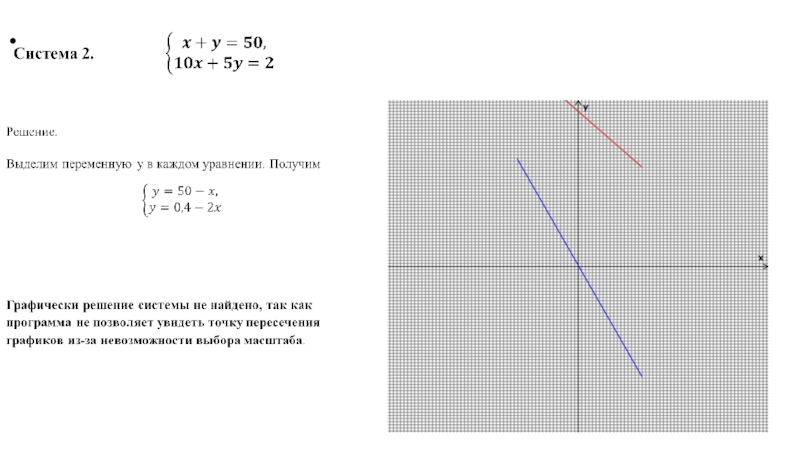
Слайд 5Плюсы и минусы графического метода решения систем уравнений.
Система 1.
Решение.
Получаем следующие
результаты:
A(-2,2;-4,5), C(2,2;4,5) – приближенные значения
B(0;5), D(4,-3) – точные значения корней.
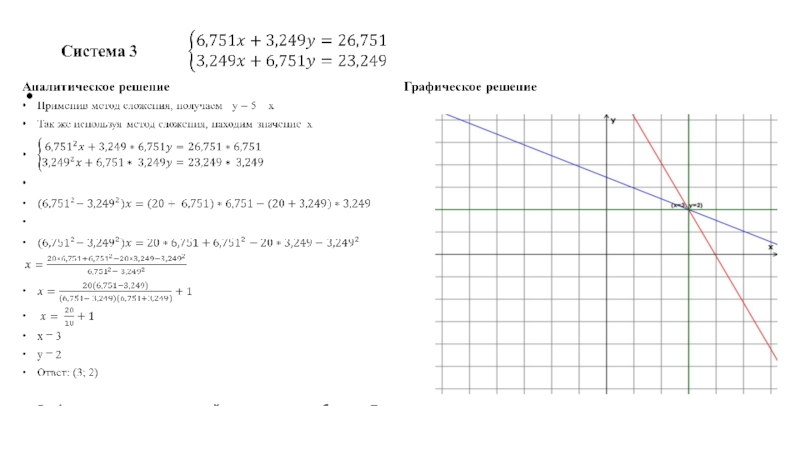
Графический метод часто используется, чтобы оценить количество корней и примерные их значения.
A(-2,2;-4,5), C(2,2;4,5) – приближенные значения
B(0;5), D(4,-3) – точные значения корней.
Графический метод часто используется, чтобы оценить количество корней и примерные их значения.
Слайд 9Заключение.
В процессе работы я понял, что графический способ не является
самым рациональным при решении систем уравнений. Не всякую систему уравнений можно решить этим методом, так как он имеет свои преимущества и недостатки.
Преимущества:
- сложно или практически невозможно решить аналитически систему уравнений
быстрота построения графиков и нахождения корней,
Наглядность и геометрическая иллюстрация наличия корней.
- полезен для проверки уже найденного решения.
Недостатки:
если система уравнений легко разрешима аналитически, то не имеет смысла решать ее графически.
- Невозможность выбора масштаба для построения графиков.
Неточность при действительных или рациональных корнях.
Преимущества:
- сложно или практически невозможно решить аналитически систему уравнений
быстрота построения графиков и нахождения корней,
Наглядность и геометрическая иллюстрация наличия корней.
- полезен для проверки уже найденного решения.
Недостатки:
если система уравнений легко разрешима аналитически, то не имеет смысла решать ее графически.
- Невозможность выбора масштаба для построения графиков.
Неточность при действительных или рациональных корнях.