Численное дифференцирование
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное дифференцирование презентация
Содержание
- 1. Численное дифференцирование
- 2. При вычислении производной функции, будем иметь в
- 3. Таким образом, вычисляется производная в середине промежутка.
- 4. Для производной третьего порядка можно использовать следующую
- 5. Односторонняя разность Производная функции определяется выражением:
- 6. Односторонняя разность Численное дифференцирование: правосторонняя разность:
- 7. Двусторонняя разность Более точное значение производной:
- 8. Формулы являются результатом дифференцирования интерполяционных многочленов Ньютона
- 9. Оценка погрешности и точности вычисления не менее
- 11. Мы будем пользоваться формулой (2), а впоследствии
- 12. Частное дифференцирование функции от многих переменных Все
- 13. Интерполяция полиномом Заданная таблица сглаживается какой-либо
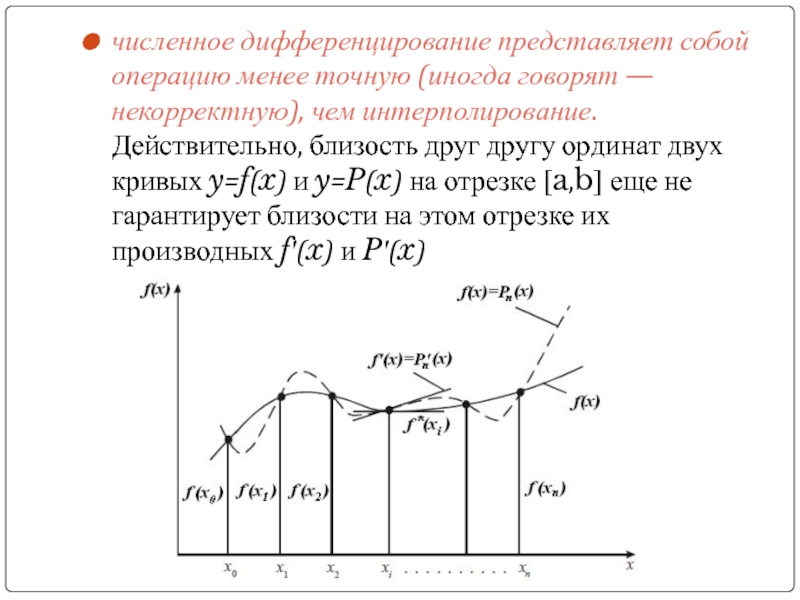
- 14. численное дифференцирование представляет собой операцию менее точную
- 15. Интерполяция конечными разностями В этом случае (x*=
- 16. Выразим yi’, разделив предварительно на h и оставляя слагаемые с первой степенью шага h, получим
- 17. где — центральная разность первого порядка
- 18. Метод Рунге С целью оценки погрешности
- 19. Из этого выражения видно, что это уже метод порядка p+1, т.е. на порядок точнее
Слайд 1К численному (приближенному) дифференцированию чаще всего прибегают, когда приходится вычислять производные
Слайд 2При вычислении производной функции, будем иметь в виду, что один из
- это взять достаточно малые значения справа и слева на равном расстоянии от
- точке, в которой мы хотим найти производную.
Слайд 3Таким образом, вычисляется производная в середине промежутка. По значениям f' можно
Слайд 4Для производной третьего порядка можно использовать следующую формулу:
Возникают естественные вопросы,
Слайд 5Односторонняя разность
Производная функции определяется выражением:
заменяем приращение на конечную величину
(шаг
x0
f(x0)
f(x0+Δx)
x0+Δx
Δx
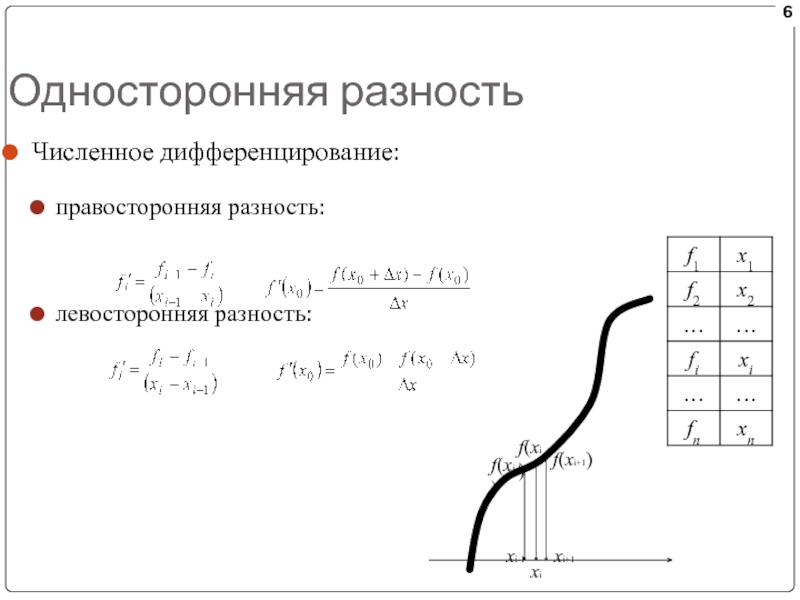
Слайд 6Односторонняя разность
Численное дифференцирование:
правосторонняя разность:
левосторонняя разность:
xi
f(xi)
f(xi+1)
xi-1
f(xi-1)
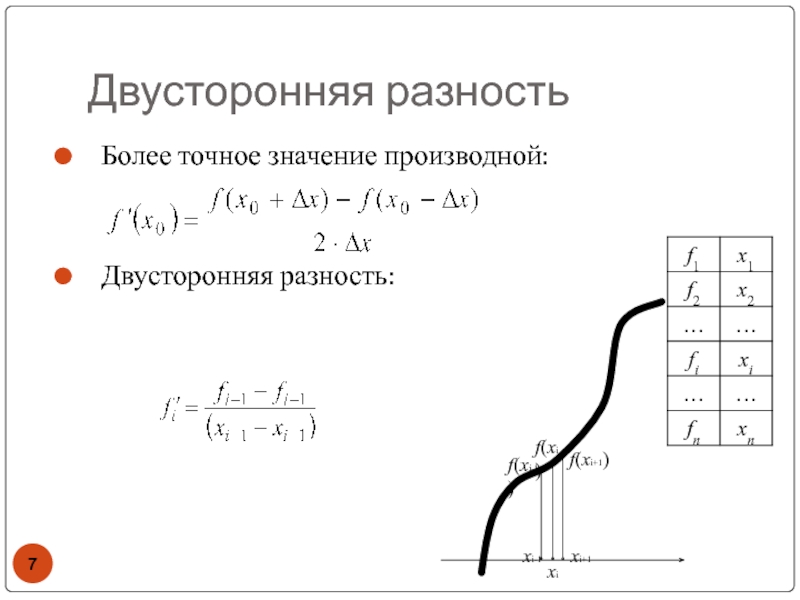
Слайд 7Двусторонняя разность
Более точное значение производной:
Двусторонняя разность:
xi
f(xi)
f(xi+1)
xi-1
f(xi-1)
Слайд 8Формулы являются результатом дифференцирования интерполяционных многочленов Ньютона и других. Сущность которых
Слайд 9Оценка погрешности и точности вычисления не менее серьезный и сложный процесс,
где предполагается, что функция f(x) дифференцируемая
n + 1 раз, а точка
- некоторое промежуточное значение между x0 - точкой, в которой находится производная и точками (x0 - 2dx), (x0 - dx), (x0 + dx), (x0 + 2dx), ...
из заданного промежутка [a, b].
(2)
Слайд 10 На практике f (n+1)(c) оценивать непросто, поэтому при малых dx приближенно
(3)
Слайд 11Мы будем пользоваться формулой (2), а впоследствии и формулой (3), в
Слайд 12Частное дифференцирование функции от многих переменных
Все аргументы функции становятся константами, кроме
Требуемый порядок производной получается путем последовательного вычисления производных, вплоть до требуемого порядка
Слайд 13Интерполяция полиномом
Заданная таблица сглаживается какой-либо функцией P(x), являющейся интерполяционным полиномом, или
f(x) = P(x) + Rn(x), f(x*) = P(x*) + Rn(x*):
f′(x) = P′(x) + R′n(x), f′(x*) = P′(x*) + R′n(x*):
f′′(x) = P′′(x) + R′′n(x), f′′(x*) = P′′(x*) + R′′n(x*)
Слайд 14численное дифференцирование представляет собой операцию менее точную (иногда говорят — некорректную),
Слайд 15Интерполяция конечными разностями
В этом случае (x*= xi , i = 0,…,
(9.3)