- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Четырехугольники 8 класс презентация
Содержание
- 1. Четырехугольники 8 класс
- 2. Четырехугольник, его елементы
- 3. Точки чотырехугольника называются вершинами, а отрезки,
- 4. Соседние стороны— стороны четырехугольника, которые выходят из
- 5. Четырехугольник называется указанием его вершин, при
- 6. Если
- 7. Параллелограмм и его свойства. Признаки параллелограмма.
- 8. У параллелограмма из каждой
- 9. Свойства параллелограмма У параллелограмма противоположные стороны
- 10. Диагонали параллелограмма пересекаются и точкой пересечения делятся
- 11. Признаки параллелограмма Если
- 12. Если в четырехугольнике противолежащие
- 13. Свойство диагоналей параллелограмма: Диагонали параллелограмма пересекаются и
- 14. Это интересно. Если провести биссектрисы двух противолежащих
- 15. Прямоугольник, его свойства Представитель класса параллелограммов -
- 16. Свойства прямоугольника Противолежащие стороны прямоугольника равны. Все
- 17. Диагонали прямоугольника пересекаются и точкою пересечения делятся
- 18. Признаки прямоугольника Если в параллелограмме все углы
- 19. Это интересно. Если в прямоугольнике
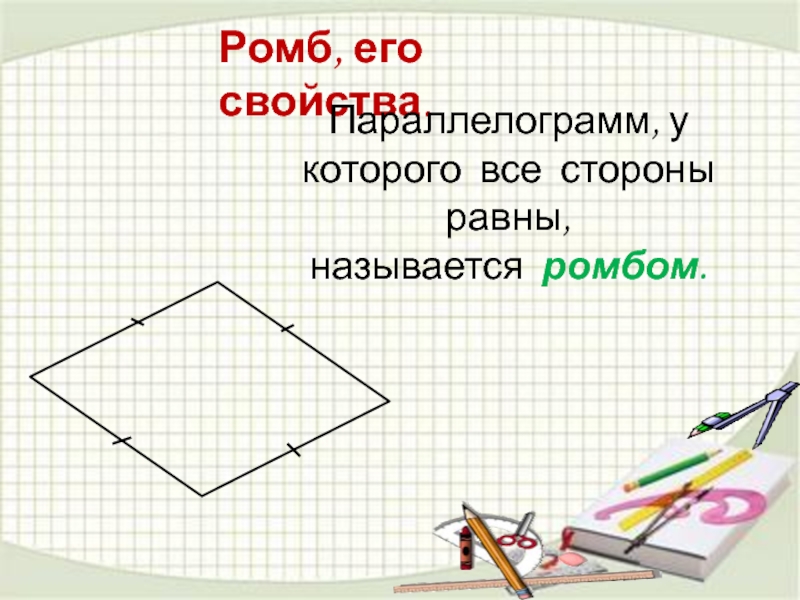
- 20. Ромб, его свойства. Параллелограмм, у которого все стороны равны, называется ромбом.
- 21. Свойства ромба Противолежащие углы ромба равны. У
- 22. Признаки ромба Если в параллелограмме диагонали
- 23. Это интересно. Если соединить отрезками средины сторон
- 24. Квадрат, его свойства Свойства квадрата Прямоугольник, у
- 25. Признаки квадрата Если в прямоугольнике диагонали
- 26. Трапеция, её свойства Четырехугольник, у которого только
- 27. Равнобедренная трапеция — это трапеция, у которой
- 28. Свойства трапеции В равнобедренной трапеции углы при
- 29. Признаки равнобедренной трапеции Если в трапеции углы
- 30. Это интересно. Если средины сторон равнобедренной трапеции соединить отрезками, то получим ромб.
- 31. Желаю удачи!
Слайд 11
Геометрия 8 класс
Раздел І:
Четырехугольники
Учитель математики
МОУ “Оленовская школа №2
Волновахского района”
Прохоренко
Слайд 2Четырехугольник, его елементы
Четырехугольник — фигура, состоящая из четырёх точек
1. На одной прямой должно лежать не больше двух точек.
2. Отрезки, соединяющие точки, не должны пересекаться.
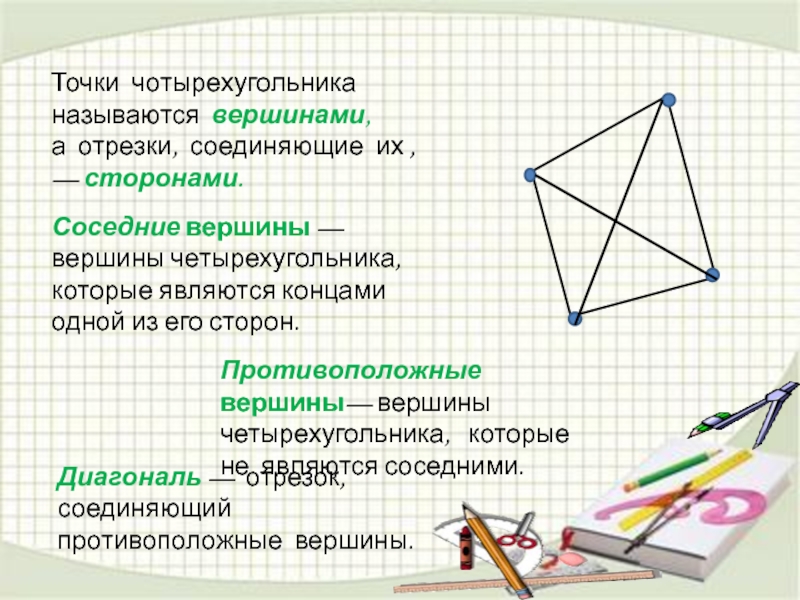
Слайд 3Точки чотырехугольника называются вершинами,
а отрезки, соединяющие их , — сторонами.
Соседние вершины
Противоположные вершины— вершины четырехугольника, которые не являются соседними.
Диагональ — отрезок, соединяющий противоположные вершины.
Слайд 4Соседние стороны— стороны четырехугольника, которые выходят из одной вершины.
Противолежащие стороны —
Периметр — сумма всех сторон четырехугольника.
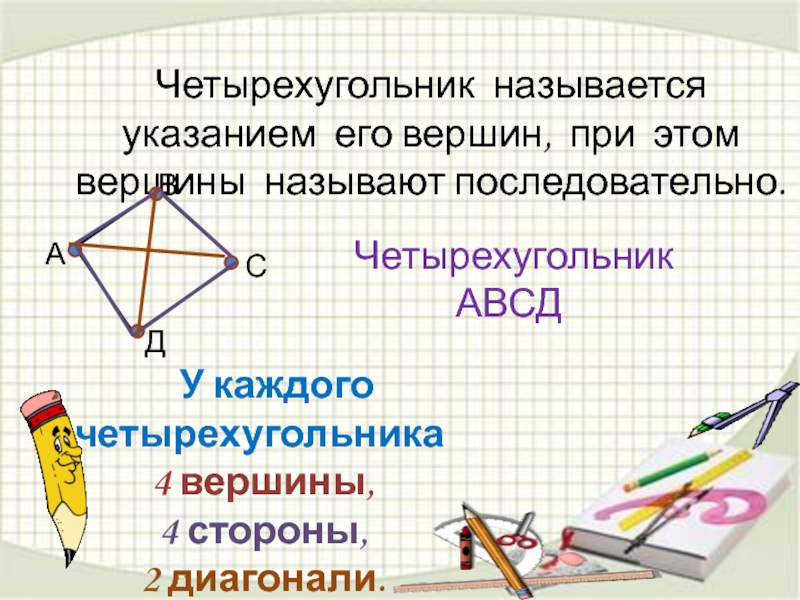
Слайд 5Четырехугольник называется указанием его вершин, при этом вершины называют последовательно.
4 вершины,
4 стороны,
2 диагонали.
А
В
С
Д
Четырехугольник АВСД
Слайд 6 Если в четырехугольнике провести
Сумма углов заданного четырехугольника будет равняться сумме углов обоих полученных треугольников.
Учитывая, что сумма углов любого треугольника равна 1800, то сумма углов заданного четырехугольника равна 360°.
Запомните!
Сумма углов любого четырехугольника равна 3600.
1800
1800
Сумма углов четырехугольника
Слайд 7Параллелограмм и его свойства.
Признаки параллелограмма.
Четырехугольник, у которого противолежащие стороны
Высотою параллелограмма называется отрезок, перпендикулярный к прямой, содержащую противоположную сторону.
АВ ││СД
А
В
С
Д
АД ││ВС
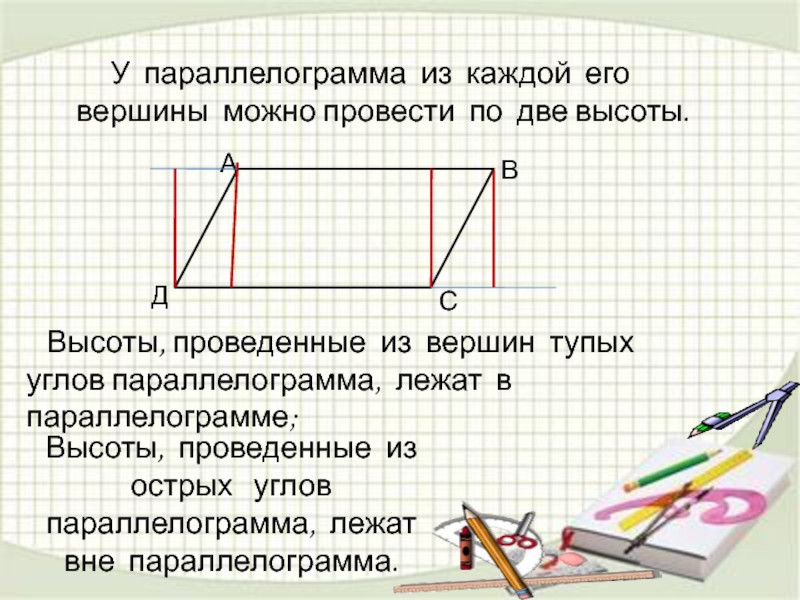
Слайд 8 У параллелограмма из каждой его вершины можно провести
Высоты, проведенные из вершин тупых углов параллелограмма, лежат в параллелограмме;
Высоты, проведенные из острых углов параллелограмма, лежат вне параллелограмма.
Д
С
А
В
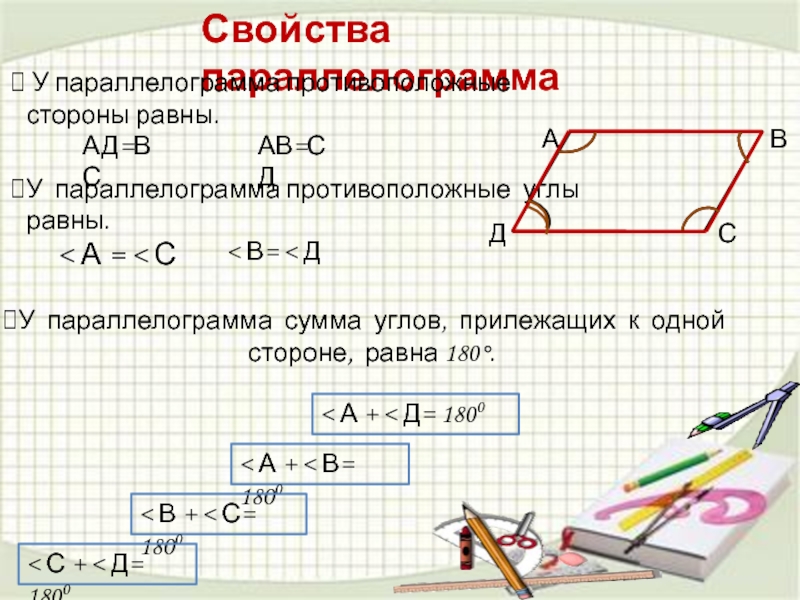
Слайд 9Свойства параллелограмма
У параллелограмма противоположные стороны равны.
У параллелограмма противоположные углы равны.
У
А В
Д С
АД=ВС
АВ=СД
< А = < С
< В= < Д
< А + < Д= 1800
< А + < В= 1800
< В + < С= 1800
< С + < Д= 1800
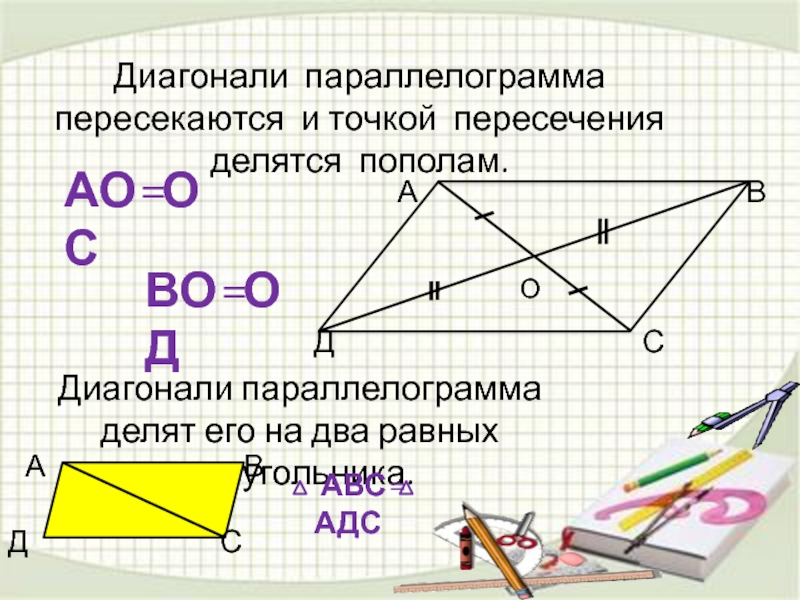
Слайд 10Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Диагонали параллелограмма делят его
А В
Д С
О
ВО=ОД
АО=ОС
А В
Д С
АВС= АДС
Слайд 11Признаки параллелограмма
Если диагонали четырехугольника пересекаются и точкой
Если в четырехугольнике две противолежащие стороны параллельны и равны, то этот четырехугольник параллелограмм.
А В
Д С
О
Если АО=ОС и ВО=ОД , то АВСД - параллелограмм
Если АВ=ДС и АВ//ДС , то
АВСД - параллелограмм
Слайд 12 Если в четырехугольнике противолежащие стороны попарно равны, то
Если в четырехугольнике противоположные углы попарно равны, то этот четырехугольник параллелограмм.
А В
Д С
То есть , если
АВ=СД
и АД=ВС ,
то АВСД - параллелограмм
То есть , если
< А = < С
и < В = < Д
то АВСД - параллелограмм
Слайд 13Свойство диагоналей параллелограмма:
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Свойство
У параллелограмма противоположные стороны и углы равны.
А В
Д С
О
АО=ОС і ВО=ОД
АВ=СД
АД=ВС
< А = < С
< В = < Д
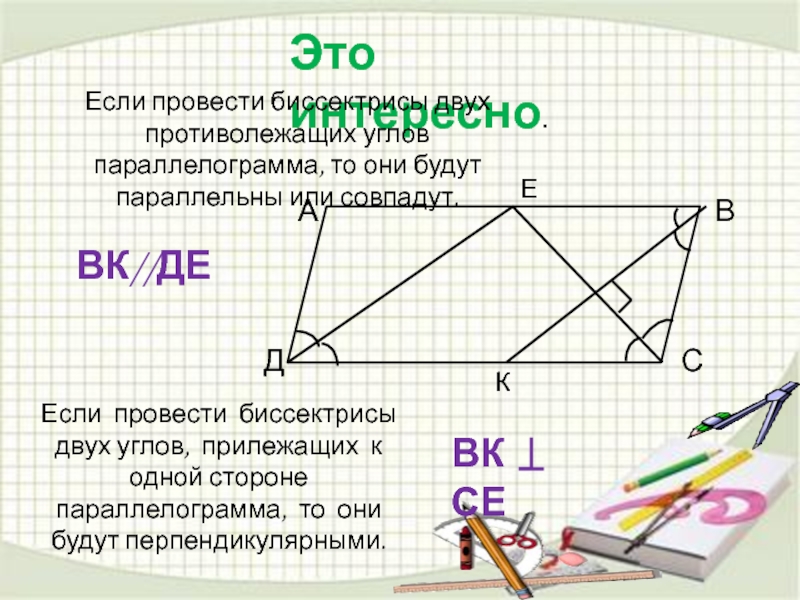
Слайд 14Это интересно.
Если провести биссектрисы двух противолежащих углов параллелограмма, то они будут
Если провести биссектрисы двух углов, прилежащих к одной стороне параллелограмма, то они будут перпендикулярными.
А В
Д С
К
Е
ВК//ДЕ
ВК СЕ
Слайд 15Прямоугольник, его свойства
Представитель класса параллелограммов - прямоугольник.
Параллелограмм, у которого все углы
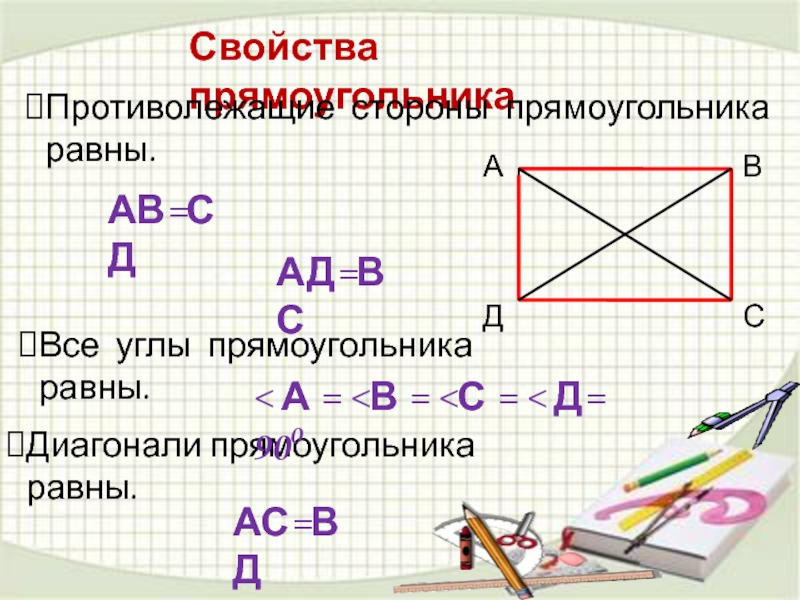
Слайд 16Свойства прямоугольника
Противолежащие стороны прямоугольника равны.
Все углы прямоугольника равны.
Диагонали прямоугольника равны.
А
Д С
АВ=СД
АД=ВС
< А = <В = <С = < Д= 900
АС=ВД
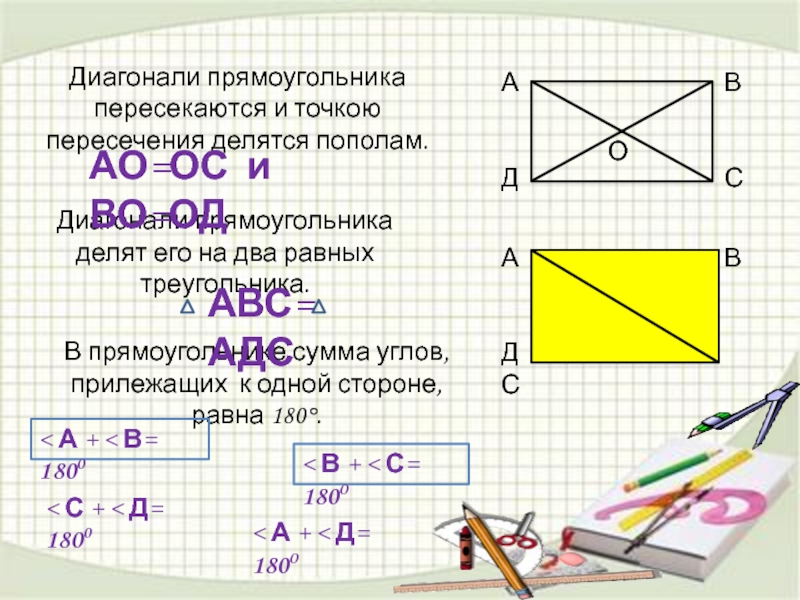
Слайд 17Диагонали прямоугольника пересекаются и точкою пересечения делятся пополам.
Диагонали прямоугольника делят его
В прямоугольнике сумма углов, прилежащих к одной стороне, равна 180°.
А В
Д С
О
АО=ОС и ВО=ОД
А В
Д С
АВС= АДС
< А + < В= 1800
< В + < С= 1800
< С + < Д= 1800
< А + < Д= 1800
Слайд 18Признаки прямоугольника
Если в параллелограмме все углы равны, то этот параллелограмм -
Если в параллелограмме один угол прямой,
то этот параллелограмм - прямоугольник.
Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник.
А В
Д С
Если < А = <В = <С = < Д , то
АВСД - прямоугольник
Если < А = 900 , то АВСД - прямоугольник
Если АС=ВД, то
АВСД - прямоугольник
Если в четырехугольнике три угла прямые, то этот четырехугольник - прямоугольник.
Если < А = <В = <С = 900 , то
АВСД - прямоугольник
Слайд 19Это интересно.
Если в прямоугольнике с неравными смежными сторонами провести
Обратите внимание!
Если в прямоугольнике проведена биссектриса, пересекающую одну из сторон, то она отсекает от прямоугольника равнобедренный треугольник.
Слайд 21Свойства ромба
Противолежащие углы ромба равны.
У ромба сумма углов, прилежащих к одной
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Диагонали ромба пересекаются и точкою пересечения делятся пополам.
А
В Д
С
< А = < С
< В = < Д
< А + < В = 1800
АС ВД
АО=ОС и ВО=ОД
О
Слайд 22Признаки ромба
Если в параллелограмме диагонали пересекаются под прямым углом, то
Если в параллелограмме диагонали являются биссектрисами его углов, то этот параллелограмм - ромб.
Если в параллелограмме две смежные стороны равны, то этот параллелограмм - ромб.
Если в четырехугольнике все стороны равны, то этот четырехугольник - ромб.
Если в параллелограмме одна из диагоналей является биссектрисою его угла, то этот параллелограмм - ромб.
Если в четырехугольнике диагонали являются биссектрисами его углов и пересекаются под прямым углом, то этот четырехугольник - ромб.
Слайд 23Это интересно.
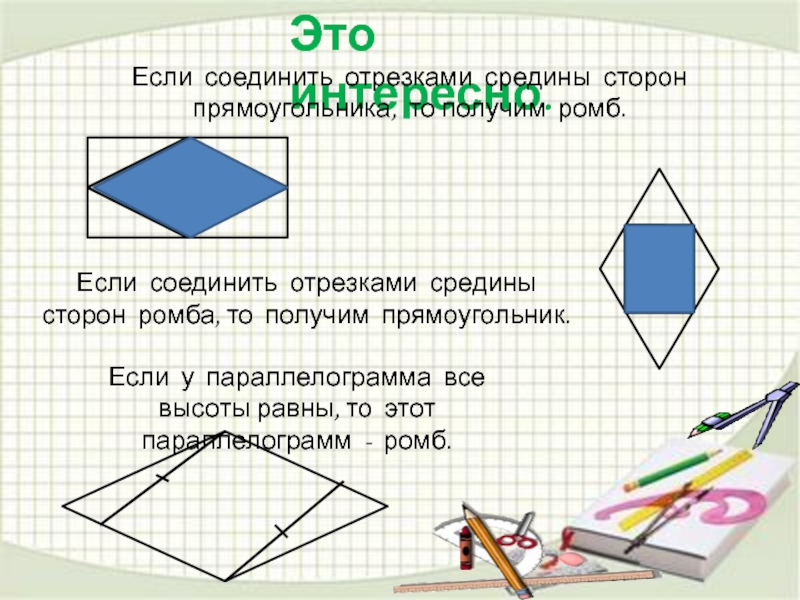
Если соединить отрезками средины сторон прямоугольника, то получим ромб.
Если соединить
Если у параллелограмма все высоты равны, то этот параллелограмм - ромб.
Слайд 24Квадрат, его свойства
Свойства квадрата
Прямоугольник, у которого все стороны равны, называются квадратом.
Диагонали
А В
Д С
Все углы квадрата — прямые.
Диагонали квадрата пересекаются и точкою пересечения делятся пополам.
Диагонали квадрата равны.
Диагонали квадрата являются биссектрисами его углов.
< А = <В = <С = < Д= 900
АО=ОС и ВО=ОД
О
АС=ВД
Слайд 25Признаки квадрата
Если в прямоугольнике диагонали пересекаются под прямым углом, то
Если у ромба диагонали равны, то этот ромб - квадрат.
Если в четырехугольнике все стороны равны и все углы равны, то этот четырехугольник - квадрат.
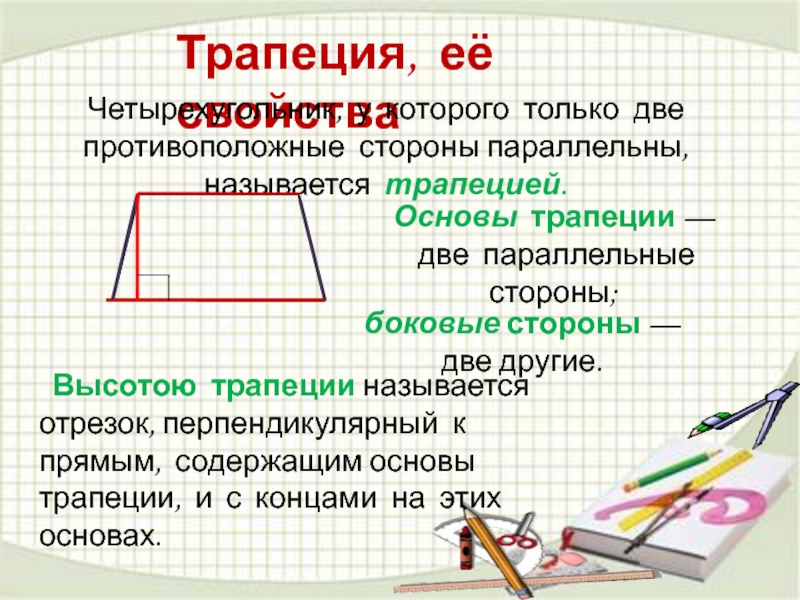
Слайд 26Трапеция, её свойства
Четырехугольник, у которого только две противоположные стороны параллельны, называется
Основы трапеции —
две параллельные стороны;
Высотою трапеции называется отрезок, перпендикулярный к прямым, содержащим основы трапеции, и с концами на этих основах.
боковые стороны — две другие.
Слайд 27Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Боковая сторона
Прямоугольная трапеция — это трапеция, одна боковая сторона которой перпендикулярна её основам.
В прямоугольной трапеции два угла прямые, один острый и один тупой.
А В
Д С
< А = < Д= 90 0
< В - тупой
< С - острый
АД = h
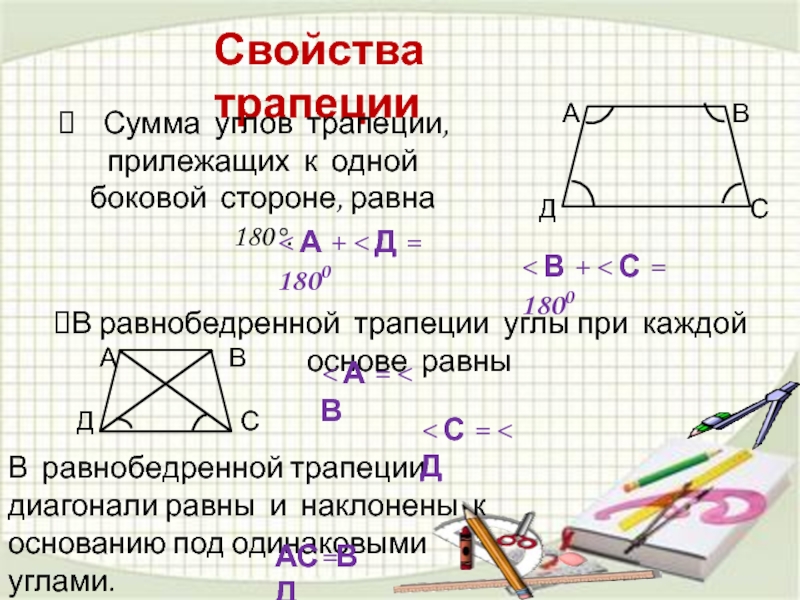
Слайд 28Свойства трапеции
В равнобедренной трапеции углы при каждой основе равны
Сумма
В равнобедренной трапеции диагонали равны и наклонены к основанию под одинаковыми углами.
А В
Д С
< А + < Д = 1800
< В + < С = 1800
А В
Д С
< А = < В
< С = < Д
АС=ВД
Слайд 29Признаки равнобедренной трапеции
Если в трапеции углы при основании равны, то трапеция
Если в трапеции диагонали равны, то трапеция равнобедренная.
Если в трапеции диагонали образуют с основаниями равные углы, то трапеция равнобедренная.
Слайд 30Это интересно.
Если средины сторон равнобедренной трапеции соединить отрезками, то получим