- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Бесконечность не предел презентация
Содержание
- 1. Бесконечность не предел
- 2. Назовите самое большое число, которое можете представить?
- 3. А может бесконечность? Нет. Бесконечность – это
- 4. Первым делом, когда число определяет как много
- 5. Алеф – это первая буква алфавита в
- 6. Суть в том, что Алеф (0) -
- 7. У обоих множеств мощность равна Алеф (0)
- 8. Вернёмся в начало, если бы мы настояли
- 9. Первый трансфинитный ординал это омега. Это не
- 10. Порядковый тип множества это просто первое ординальное
- 11. Но Алеф (0) это не конец. Почему
- 12. Всё, что необходимо сделать, чтобы получить Омегу
- 13. Сверх эти и через эти мы дойдём
- 14. Это предположение утверждает , что если взять
- 15. В итоге мы дойдём до Омеги в
- 16. Преобразование позволяет делать с каждым шагом всё
- 17. Мы также говорили о преодоление конечный до
- 18. Миллион в степени миллион в степени миллион,
- 19. Интересен тот факт, что большинство или даже
Слайд 2Назовите самое большое число, которое можете представить? Гугл? Гуголплекс? Гуголплексплекс? Что
же, в реальности самое большое число – это сорок, занимает оно более 12 тысяч квадратных метров земли. Число сорок сделано из специально высаженных деревьев в России. Сорок – самое большое число, на Земле, говоря о площади поверхности, но говоря о количестве вещей, то есть о том что мы обычно подразумеваем под обычным числом сорок вероятно не самое большое, например есть, 41 ну ещё есть 42 и 43, миллиард , триллион.
Слайд 3А может бесконечность? Нет. Бесконечность – это не число, скорее разновидность
числа. Бесконечные числа необходимы, чтобы говорит о количествах, и сравнивать их, которые не кончаются. Но некоторые нескончаемые количества, некоторые бесконечности, буквально больше, чем другие. Давайте взглянем на некоторые из них и посчитаем сверх них.
Слайд 4Первым делом, когда число определяет как много чего-либо, оно называется количественным
числом. Например, 4 банана, 20 точек, 20 – это мощность этого множества точек. Мы используем натуральные числа 0 1 2 3 4 5 и т.д. как количественные, всякий раз когда говорим, как много чего – либо, но сколько всего натуральных чисел? Этим числом не может быть число среди натуральных , потому что всегда было бы 1 + это число. Поэтому придумали специальное имя этому количеству Алеф(0).
Слайд 5Алеф – это первая буква алфавита в иврите, а Алеф (0)
- это самая первая маленькая бесконечность. Количество всех натуральных чисел, а также количество всех четных , нечетных, рациональных чисел, то есть дробей. Может это звучит удивительно, так как дробей появляется гораздо больше. Но, как показал Кантор, есть способ расположить каждое рациональное число, так что натуральные числа можно сопоставить 1 к 1 с рациональными. У них одинаковая мощность
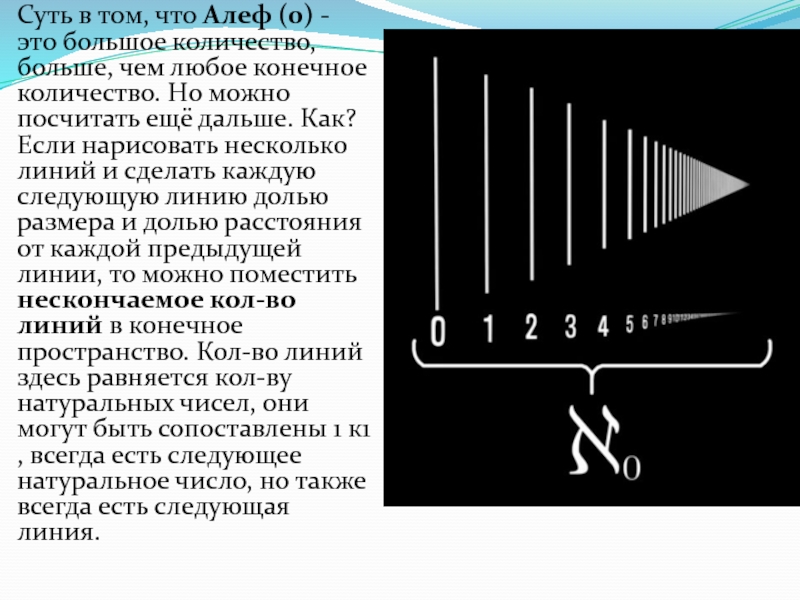
Слайд 6Суть в том, что Алеф (0) - это большое количество, больше,
чем любое конечное количество. Но можно посчитать ещё дальше. Как? Если нарисовать несколько линий и сделать каждую следующую линию долью размера и долью расстояния от каждой предыдущей линии, то можно поместить нескончаемое кол-во линий в конечное пространство. Кол-во линий здесь равняется кол-ву натуральных чисел, они могут быть сопоставлены 1 к1 , всегда есть следующее натуральное число, но также всегда есть следующая линия.
Слайд 7У обоих множеств мощность равна Алеф (0) Но что произойдёт ,
если добавить ещё 1 линию? А теперь, сколько тут линий? Алеф(0) + 1? Нет! Нескончаемые кол-ва не такие, как конечные кол-ва, тут всё ещё Алеф (0) линий, потому что можно подставить натуральные числа 1 к 1 как и раньше. Просто начнём отсюда, а потом продолжим сначала. Несомненно, кол-во линий не изменилось. В итоге всегда получается Алеф (0) линий. Если дело не в количестве составляющих, тогда в чём?
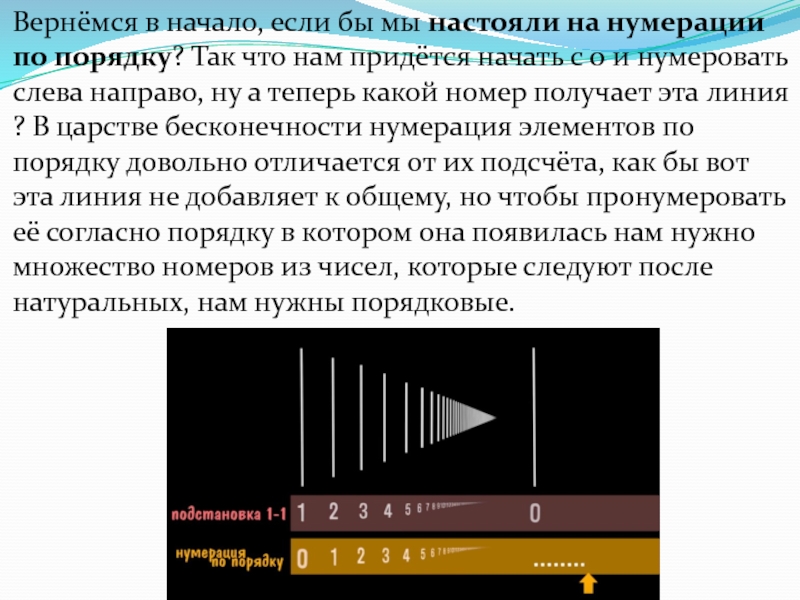
Слайд 8Вернёмся в начало, если бы мы настояли на нумерации по порядку?
Так что нам придётся начать с 0 и нумеровать слева направо, ну а теперь какой номер получает эта линия ? В царстве бесконечности нумерация элементов по порядку довольно отличается от их подсчёта, как бы вот эта линия не добавляет к общему, но чтобы пронумеровать её согласно порядку в котором она появилась нам нужно множество номеров из чисел, которые следуют после натуральных, нам нужны порядковые.
Слайд 9Первый трансфинитный ординал это омега. Это не шутка и не фокус,
это буквально следующее число, которое останется после исчерпания каждого счётного числа в итоге. Если вы заняли Омега В место в гонке это означало бы, что бесконечное число людей пришло к финишу, и потом пришли вы. После омеги идёт Омега + 1, что не совсем- то похоже на число, но это число, такое же как 2 или 12, потом Омега +2. Суть ординалов не в количестве элементов, они показывают нам , как эти элементы расположены, их порядковый тип.
(Омега+ 1 не чуть не больше чем Омега , она просто идёт после)
(Омега+ 1 не чуть не больше чем Омега , она просто идёт после)
Слайд 10Порядковый тип множества это просто первое ординальное число не нужное для
нумерации всего во множестве по порядку. Так для конечных чисел мощность множества и порядковый тип одинаковы. Порядковый тип всех натуральных чисел это омега. Порядковый тип следующей последовательности Омега +1 и так далее. Не важно какой длины станет последовательность, при условии , что она вполне упорядочена и каждая её часть содержит начальный элемент. Всё это описывает новое ординальное число.
Слайд 11Но Алеф (0) это не конец. Почему же? Да потому что
существуют бесконечности больше, чем Алеф (0). Сфокусируемся на кое на чём другом, ещё большем, чем Алеф(0) – Булеан Алефа (0). Булеан множества – это группа всех разных подмножеств, которые можно сделать из него. Булеан (Алеф(0)) > Алеф(0) . Это отличный способ создавать всё более большие и большие бесконечности. Дело в том, что существуют кардиналы, большие , чем Алеф (0). Попробуем добраться до них. Не забываем, что после омеги, ординалы отделяются, и эти числа уже больше не кардиналы. Они не ссылаются на большее кол-во, чем последний достигнутый нами кардинал.
Слайд 12Всё, что необходимо сделать, чтобы получить Омегу это сказать : “Да
будет Омега” ( То есть принять это как факт) И этого достаточно. Так и поступил Эрнест Мэлоу в 1908 когда он включил аксиому бесконечности в своей список аксиом. Аксиома бесконечности гласит, что одно бесконечное множество существует - множество всех натуральных чисел. Если вы отказываетесь это принять, ничего страшного , значит что вы фенетист и верите что только конечные вещи существуют, но если вы согласны. То можно пойти ещё дальше.
Слайд 13Сверх эти и через эти мы дойдём до омеги + омега,
разве только мы достигли ещё одного потолка. Чтобы пройти весь этот путь до омеги + омега нужно создать ещё одно бесконечное множество. А аксиома бесконечно гарантирует, что есть только это множество, множество натуральных чисел. Придётся ли нам добавлять новую аксиому, каждый раз когда мы описываем Алеф(0) чисел? Нет. Здесь нам поможет схема преобразования множеств.
Слайд 14Это предположение утверждает , что если взять множество , скажем множество
натуральных чисел и заменить каждый элемент чем-то других, например, бананами , что у нас получиться, тоже является множеством. Возьмём каждый ординал вплоть до омеги и потом вместо бананов поставим омега + перед каждым, теперь мы достигли Омега+ Омега или омега дважды. Используя преобразования можно делать скачки, хоть какого размера. До тех пор пока мы используем те числа, которых мы достигли. Можно преобразовать каждый ординал вплоть до омеги омегой умноженное на это число, чтобы достичь омега * омега. Схема преобразования позволяет собирать нам новые ординалы без конца.
Слайд 15В итоге мы дойдём до Омеги в степени омега в степени
омега и т.д. и тогда у нас заканчиваются стандартные математические обозначения. Не проблема, это просто называется E(0), и мы продолжаем уже отсюда . А теперь подумайте обо всех этих ординалах, обо всех разных способах разложить Алеф(0) элементов. А такой ординал, который стоит после, них всех называется Омега (1). Иначе же говоря Алеф (1). Пойдём всё дальше и дальше к новым бесконечностям. Теперь используя схему преобразования, можно использовать любой ординал, которого мы достигли, например, Омегу и прыгать от Алеф к Алеф, весь путь до Алеф( омега), также мы можем собрать Алеф (Омега в квадрате), а далее дойти до Алеф (омега (омега (омега)).
Слайд 16Преобразование позволяет делать с каждым шагом всё более и более большие
скачки. Всё это дело безумно ускоряющийся цикл обратной связи увеличения. Можно продолжать всё это делать, достигать больших и больших бесконечностей. Преобразование и повторные булеаны которые могут совпадать с Алефами, а могут и нет, будут продолжать наше восхождение вечно. Наверно, за их пределами ничего нет? Конечно есть.
Слайд 17Мы также говорили о преодоление конечный до омеги, почему бы не
принять как аксиому, что существует какое-то следующее число, такое большое, что даже при помощи несчётного кол-ва преобразований или булеанов чего-либо меньшего мы не сможем добраться до него. Такое число называется Недостижимым кардиналом, потому что его невозможно достичь снизу. В наших числах, которых мы уже достигли, можно найти тень Недостижимого кардинала – это Алеф(0), его тоже нельзя достичь снизу. Все числа ниже его конечные, а конечное число конечных чисел не может быть прибавлено , умножено, возведено в степень и не получить ещё одно конечное кол-во.
Слайд 18Миллион в степени миллион в степени миллион, невероятно большое число, но
оно всё равно конечное и даже не близко к Алеф(0) – первой наименьшей бесконечности. По этой причине Алеф(0) называют недостижимым числом. Единственное, что остаётся это провозгласить его существование аксиоматически. Придётся также сделать это для недостижимых кардиналов. На самом деле очень сложно понять насколько непостижим размер недостижимого кардинала. Скачок от 0 до Алеф(0) – это тоже самое, что скачок от Алеф(0) до недостижимого кардинала.
Слайд 19Интересен тот факт, что большинство или даже все бесконечности настолько большие,
что мы не можем сказать, есть ли они на самом деле или могут быть показаны в пределах физической вселенной. Если могут , если физики когда - нибудь найдут им применение – это отлично. Если нет – то это тоже отлично. Это будет означать, что мы с таким вот мозгом нашли что- то истинное за пределами физической реальности, что-то , что применимо в реальном мире, но также достаточно сильное, чтобы пойти дальше сверх того что даже сама вселенная может содержать или показать нам или быть.