способ формирования метапредметных результатов обучения в условиях реализации ФГОС»
Шулениной Веры Ивановны
МАОУ СШ № 51 г. Липецка
На тему:
Рабочая программа математического кружка «Эрудит»
для 5-6 классов
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аттестационная работа. Рабочая программа математического кружка Эрудит. (5-6 класс) презентация
Содержание
- 1. Аттестационная работа. Рабочая программа математического кружка Эрудит. (5-6 класс)
- 2. Математический кружок – это объединение
- 3. Большая роль при изучении математики
- 4. Методы, используемые во внеклассной работе
- 5. Цель кружка: создание условий для развития интереса
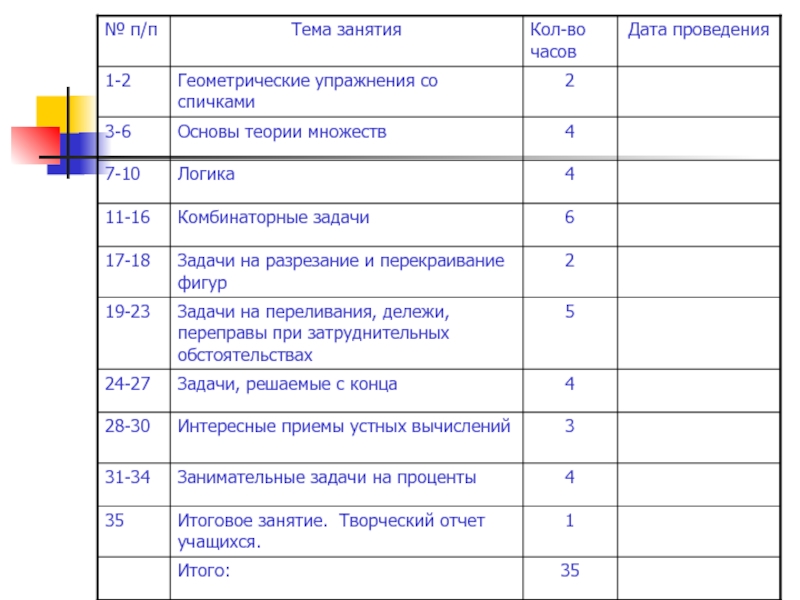
- 6. Содержание изучаемого курса
- 7. Задачи на переливания, дележи, переправы при затруднительных
- 8. Тематическое планирование
- 10. В результате изучения
- 11. Методы диагностики образовательного результата: Наблюдение, беседа, моделирующий
- 12. Список литературы 1. Энциклопедия для детей. Т.11.:
Слайд 1
Аттестационная работа
Слушателя курсов повышения квалификации по программе:
«Проектная и исследовательская деятельность как
Слайд 2 Математический кружок – это объединение учащихся под руководством педагога,
в рамках которого проводятся систематические занятия с учащимися во внеурочное время. Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования.
Пояснительная записка
Слайд 3 Большая роль при изучении математики 5 - 6 классов
отводится решению текстовых задач, работе с натуральными числами и десятичными дробями, геометрическому материалу. Курс предназначен для учащихся, склонных к занятиям математикой,- желающих повысить свой математический уровень, является предметным по содержанию, то есть, создан в поддержку предмета «математика».
Курс направлен на развитие логического мышления учащегося, на умение создавать математические модели практических задач, на расширение математического кругозора учащихся, является пропедевтикой «олимпиадных» задач.
Слайд 4 Методы, используемые во внеклассной работе по предмету, отличаются от
основных методов обучения не только содержанием, сколько формой. Кроме традиционных методов: слово учителя, беседа, самостоятельная работа учащихся, работа в группах, большое место занимают дидактические игры, содержание которых способствует развитию мыслительных операций, освоению вычислительных приемов, навыков в беглости счета и т.д.
Слайд 5Цель кружка: создание условий для развития интереса учащихся к математике.
Задачи кружка:
-
сформировать представление о методах и способах решения арифметических задач;
- развить комбинаторные способности учащихся;
- научить детей переносить знания и умения в новую, нестандартную ситуацию;
- воспитать творческую активность учащихся в процессе изучения математики;
- оказать конкретную помощь обучающимся в решении олимпиадных задач;
- способствовать повышению интереса к математике, развитию логического мышления.
- развить комбинаторные способности учащихся;
- научить детей переносить знания и умения в новую, нестандартную ситуацию;
- воспитать творческую активность учащихся в процессе изучения математики;
- оказать конкретную помощь обучающимся в решении олимпиадных задач;
- способствовать повышению интереса к математике, развитию логического мышления.
Слайд 6 Содержание изучаемого курса Геометрические упражнения со спичками
- 2 часа
Сто. Три. Дом. Рак. Весы. Основы теории множеств - 4 часа Множества и подмножества. Способы задания множеств. Операции над множествами. Диаграммы Эйлера-Венна. Логика – 4 часа Высказывания. Общие утверждения. «Хотя бы один». О доказательстве общих утверждений. Понятие отрицания. Отрицание общих высказываний. Отрицание высказываний о существовании. Комбинаторные задачи - 6 часов Перебор. Дерево из вариантов. Формирование таблиц. Умножение.
Задачи на разрезание и перекраивание фигур - 2 часа
Прямоугольник. Квадрат. Правильный шестиугольник.
Слайд 7Задачи на переливания, дележи, переправы при затруднительных обстоятельствах - 5
часов Кто прав? Спор. Дележ между двумя. Дележ между тремя. Дележ пополам. Дележ кваса. Волк, коза, капуста. Переправа трех (четырех) рыцарей с оруженосцами. Переправа через реку с островом. Через ров. Задачи, решаемые с конца - 4 часа Магия чисел. Яблоки. Туристы. Гуси. Крестьянин и царь. И т.д. Интересные приемы устных вычислений – 3 часа Как сосчитать? Сумма последовательных чисел. Сумма натуральных чисел. Сумма нечетных чисел. Быстрое возведение в квадрат. Интересное число. Найти число. Движение пальца. Занимательные задачи на проценты - 4 часа Задачи на вклады. Задачи на скидки. Итоговое занятие – 1 час Творческий отчет учащихся.
Слайд 10 В результате изучения курса учащиеся будут уметь: -
Решать основные виды логических задач. Знать способы решения популярных логических задач.
- Применять основные принципы математического моделирования, основные свойства делимости чисел.
- Уметь решать задачи на %.
- Определять тип задачи и алгоритм ее решения.
- Решать простейшие комбинаторные задачи.
- Подбирать дополнительный материал по теме.
- Вести диалог по материалу учебных тем.
- Уметь работать самостоятельно, в паре, в группе.
Слайд 11Методы диагностики образовательного результата: Наблюдение, беседа, моделирующий эксперимент, тестирование. Методическое обеспечение дополнительной
образовательной программы:
Фарков А.В. Математические олимпиады: методика подготовки. 5-8 классы. – М.: «ВАКО», 2015.
Слайд 12Список литературы 1. Энциклопедия для детей. Т.11.: Математика. – М.: Аванта +,
2003.
2. Баврин И.И., Фрибус Е.А. Старинные задачи. – М. : Просвещение, 1994.
3. Фарков А.В. Математические олимпиады в школе: 5-11 классы. – М.: Айрис - Пресс, 2005.
4. http: //www.kvant.info/ Научно-популярный физико-математический журнал для школьников и студентов «Квант».
5. Левитас Г.Г.Нестандартные задачи по математике.- М.: ИЛЕКСА, 2007.
6. Делман И.Я., Виленкин Н.Я. За страницами учебника математики: 5-6 классы. – М.: Просвещение, 2004.
7. Братусь Т.А. и др. «Все задачи «Кенгуру», Санкт-Петербург, 2008
8. Васильев Н.Б. и др. «Заочные математические олимпиады», Москва, Наука, 1981
9. Лоповок Л.М. «1000 проблемных задач по математике», Москва, Просвещение, 1995
10. Нагибин Ф.Ф., Канин Е.С. «Математическая шкатулка», Москва, Просвещение, 1984
11. Фальке Л.Я. «Час занимательной математики», Ставрополь, Сервис школа, 2005