- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Асимптоты. Построение эскизов графиков презентация
Содержание
- 1. Асимптоты. Построение эскизов графиков
- 2. 2 Определение: прямая вида x=a называется вертикальной асимптотой для y=f(x), если
- 3. 1 Определение: прямая вида y=b называется горизонтальной асимптотой, если
- 4. 2
- 5. Определение: прямая вида y=kx+b называется наклонной асимптотой, если для y=f(x)
- 6. Примечания: 1. Вертикальные асимптоты существуют в точках
- 7. Области существования графика на координатной плоскости.
- 8. Нахождение асимптот и построение эскизов графиков
- 9. Нахождение асимптот и построение эскизов графиков
- 10. x=2, x=1, x=-2 Вертикальные асимптоты y=0 – горизонтальная асимптота
- 11. Вертикальных асимптот нет. Горизонтальных асимптот нет. Наклонная
- 12. Нахождение асимптот и построение эскизов графиков Вертик.
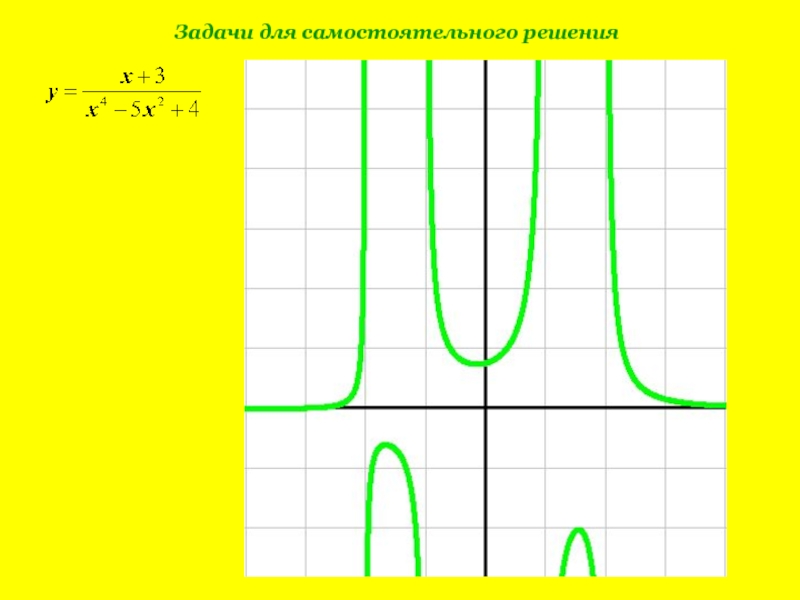
- 13. Задачи для самостоятельного решения
- 14. Задачи для самостоятельного решения
- 15. Задачи для самостоятельного решения
- 16. Задачи для самостоятельного решения
- 17. Задачи для самостоятельного решения
- 18. Литература: Богомолов Н.В. «Практические занятия по математике»,
Слайд 6Примечания:
1. Вертикальные асимптоты существуют в точках разрыва функции.
2. У дробно-рациональной функции
горизонтальные асимптоты существуют, если степень числителя меньше или равна степени знаменателя.
3. У дробно-рациональной функции наклонная асимптота существует, если степень числителя больше, чем степень знаменателя.
4. Для более точного построения эскиза нужно найти:
промежутки знакопостоянства функции
нули функции
точки пересечения графика с осями (по возможности) и с асимптотами
Слайд 7Области существования графика на координатной плоскости.
-4
-2
2
+
-
+
-
-4
-2
2
Если y>0, то график расположен выше
оси ОХ
Если y<0, то график расположен ниже оси ОХ
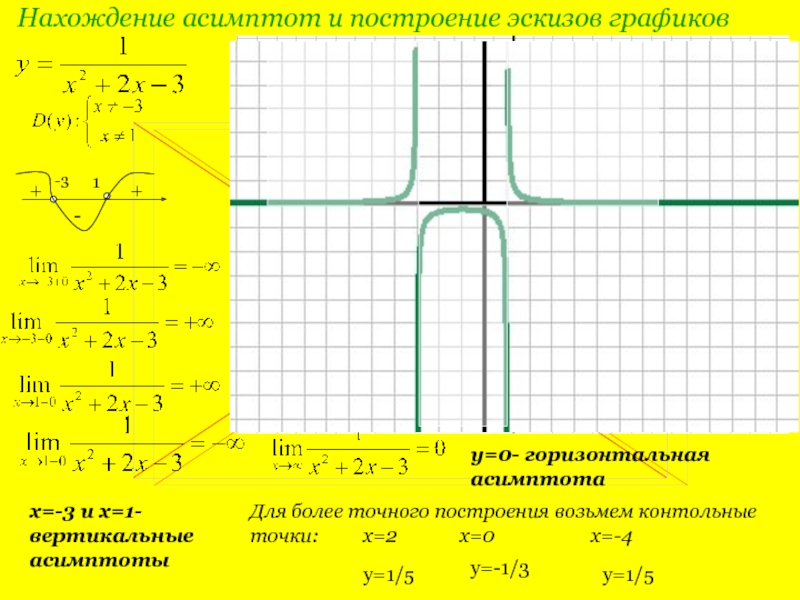
Слайд 8Нахождение асимптот и построение эскизов графиков
-3
1
+
-
+
1
-3
x=-3 и x=1-вертикальные асимптоты
y=0- горизонтальная асимптота
Для
более точного построения возьмем контольные точки: x=2 x=0 x=-4
y=1/5
y=-1/3
y=1/5
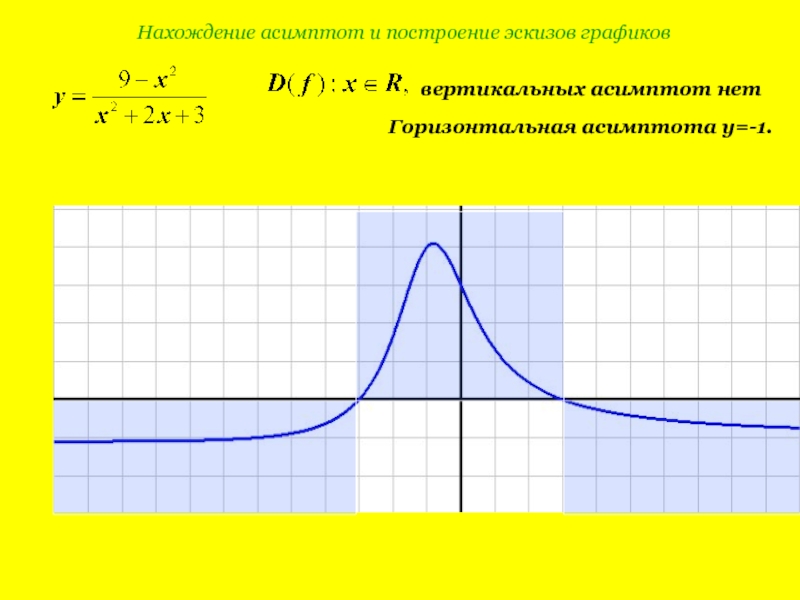
Слайд 9Нахождение асимптот и построение эскизов графиков
вертикальных асимптот нет
Горизонтальная асимптота y=-1.
Слайд 11Вертикальных асимптот нет.
Горизонтальных асимптот нет.
Наклонная асимптота y=x+2
При x=4/3 график
y=f(x) пересекает y=x+2
в точке у=3 1/3
Нахождение асимптот и построение эскизов графиков
Слайд 12Нахождение асимптот и построение эскизов графиков
Вертик. асимптота x=2
2
Горизонт. асимптот нет
-2
Нуль функции
x=-2
Наклонная асимптота y=x+4
Найдем Е(y):
Слайд 18Литература:
Богомолов Н.В. «Практические занятия по математике», М. «Просвещение»2010
А.Х.Шахмейстер «Построение графиков
функции элементарными методами»,Издательство Московского университета, МЦНМО,2003
