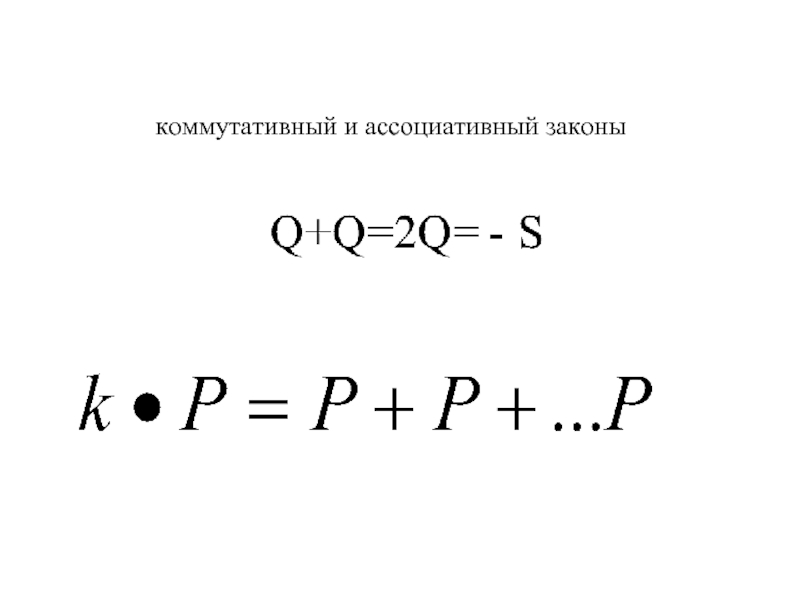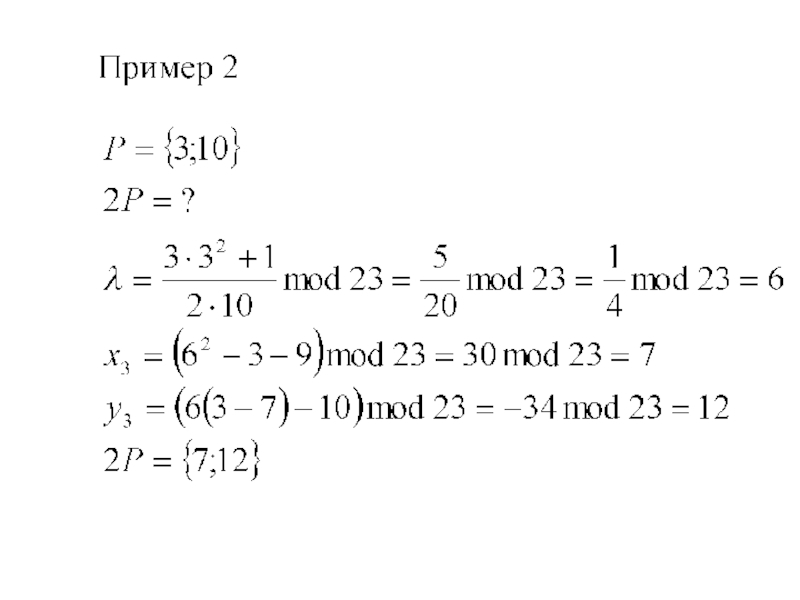- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Асимметричные алгоритмы. Продолжение презентация
Содержание
- 1. Асимметричные алгоритмы. Продолжение
- 2. Предположим, что обоим абонентам известны некоторые два
- 3. При работе алгоритма, каждая сторона: генерирует случайное
- 4. Алгоритм Диффи-Хеллмана работает на линиях связи, надежно
- 5. Криптографическая стойкость алгоритма Диффи — Хеллмана (то
- 6. Схема Эль-Гамаля (Elgamal) — криптосистема, предложенная в
- 7. Генерация ключей Генерируется случайное простое число p
- 8. Шифрование Сообщение М шифруется так: Выбирается случайное
- 9. Криптостойкость данной схемы основана на вычислительной сложности
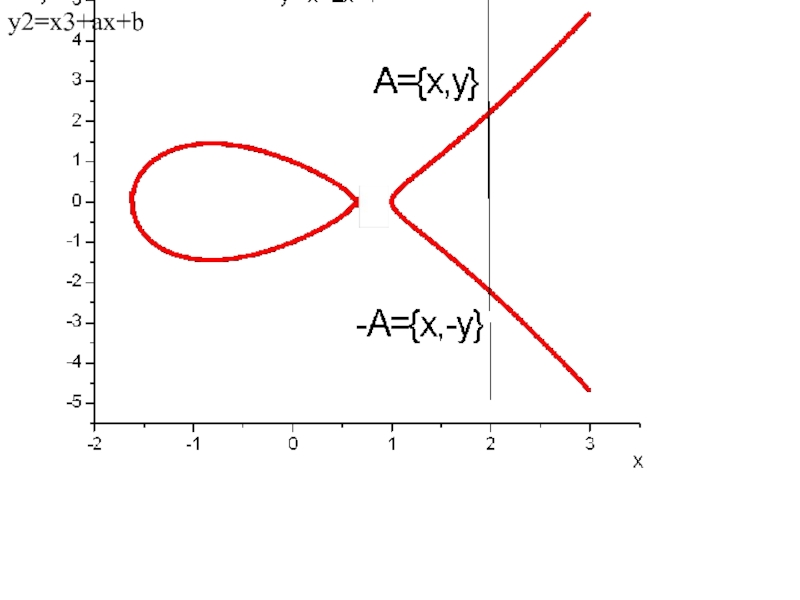
- 12. y2=x3+ax+b
- 16. Сложение
- 17. коммутативный и ассоциативный законы
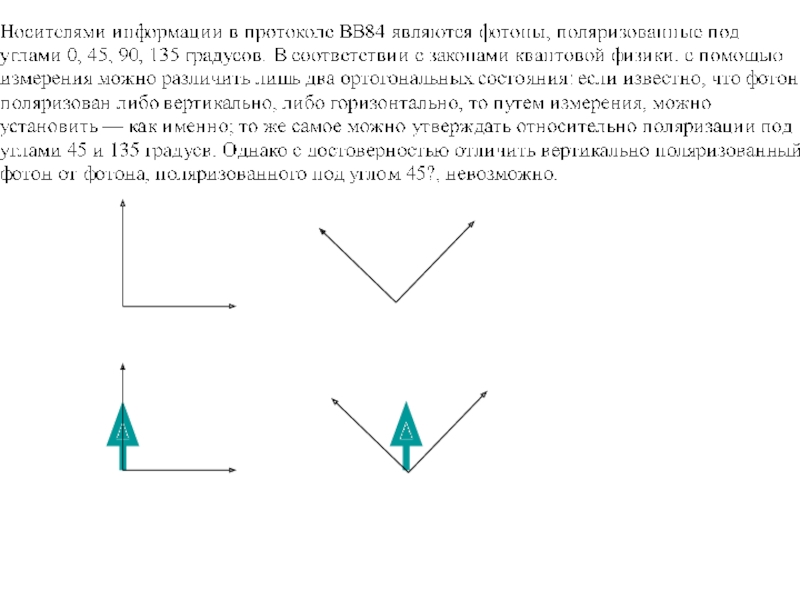
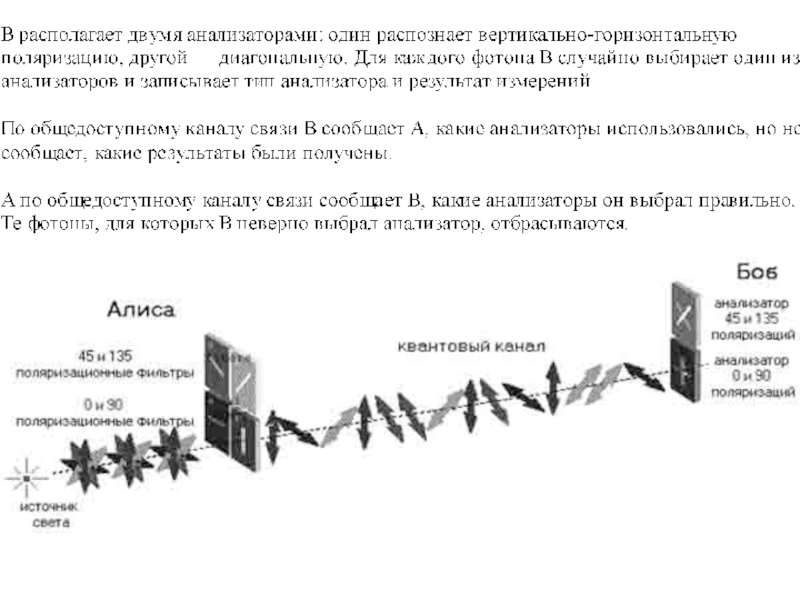
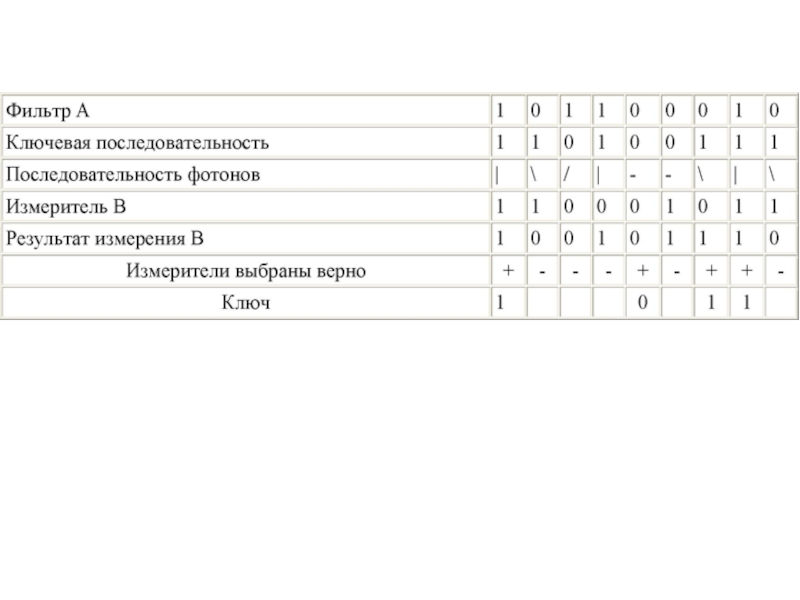
- 28. Квантовое распространение ключа
- 29. Квантовый объект: 1. Измерение изменяет состояния
- 30. Квантовое распространение ключа
- 31. Идея использовать квантовые объекты для защиты информации
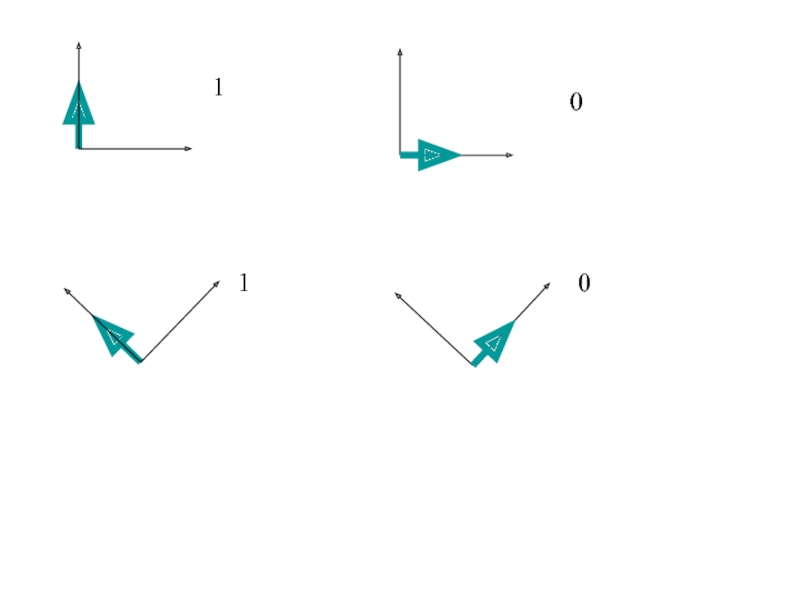
- 33. 0 0 1 1
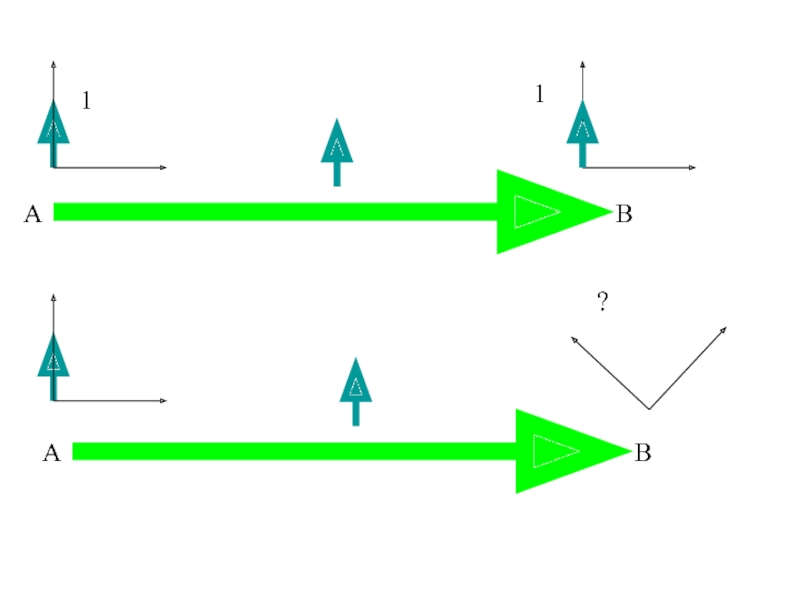
- 34. ? 1 1
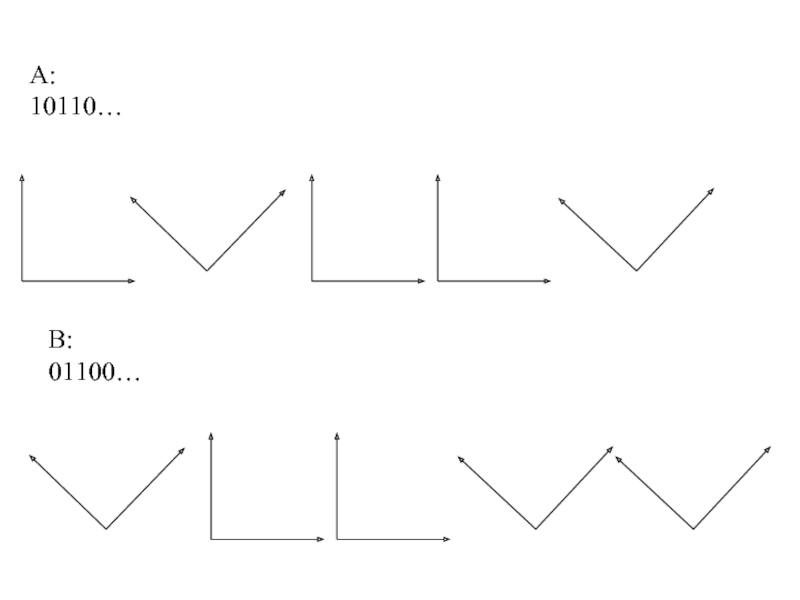
- 35. A: 10110… B: 01100…
- 38. 1989 г. В Уотсоновском исследовательском центре IBM
Слайд 2Предположим, что обоим абонентам известны некоторые два числа g и p
Слайд 3При работе алгоритма, каждая сторона:
генерирует случайное натуральное число a — закрытый
совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где
p является случайным простым числом
g является первообразным корнем по модулю p
вычисляет открытый ключ A, используя преобразование над закрытым ключом
A = ga mod p
обменивается открытыми ключами с удалённой стороной
вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a
K = Ba mod p
К получается равным с обеих сторон, потому что:
Ba mod p = (gb mod p)a mod p = gab mod p = (ga mod p)b mod p = Ab mod p
В практических реализациях, для a и b используются числа порядка 10100 и p порядка 10300. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка.
Слайд 4Алгоритм Диффи-Хеллмана работает на линиях связи, надежно защищенных от модификации. Однако,
Для защиты используются различные варианты надежной аутитификации.
Атака с подставкой (Man-in-the-middle attack): Две стороны обмениваются ключами для секретной коммуникации. Противник внедряется между ними на линии обмена сообщениями. Далее противник выдает каждой стороне свои ключи. В результате, каждая из сторон будет иметь разные ключи, каждый из которых известен противнику. Теперь противник будет расшифровывать каждое сообщение своим ключом и затем зашифровывать его с помощью другого ключа перед отправкой адресату. Стороны будут иметь иллюзию секретной переписки, в то время как на самом деле противник читает все сообщения.
Одним из способов предотвратить такой тип атак заключается в том, что стороны при обмене ключами вычисляют криптографическую хэш-функцию значения протокола обмена (или по меньшей мере значения ключей), подписывают ее алгоритмом цифровой подписи и посылают подпись другой стороне. Получатель проверит подпись и то, что значение хэш-функции совпадает с вычисленным значением. Такой метод используется, в частности, в системе Фотурис (Photuris).
Слайд 5Криптографическая стойкость алгоритма Диффи — Хеллмана (то есть сложность вычисления K=gab
Слайд 6Схема Эль-Гамаля (Elgamal) — криптосистема, предложенная в 1984 году. Схема Эль-Гамаля
Схема Эль-Гамаля
Слайд 7Генерация ключей
Генерируется случайное простое число p длины n.
Выбирается произвольное целое
Выбирается случайное число x из интервала (1,p).
Вычисляется y = gx mod p.
Открытым ключом является тройка (p,g,y),
закрытым ключом — число x.
Слайд 8Шифрование
Сообщение М шифруется так:
Выбирается случайное секретное число k из отрезка [1,
Вычисляется a = gk mod p, b = yk M mod p,
где M — исходное сообщение.
Пара чисел (a,b) является шифротекстом.
Длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения M вдвое.
Дешифрование
Зная закрытый ключ x, исходное сообщение можно вычислить из шифротекста (a,b) по формуле:
При этом нетрудно проверить, что
и .
Слайд 9Криптостойкость данной схемы основана на вычислительной сложности проблемы дискретного логарифмирования, где
Слайд 29Квантовый объект:
1. Измерение изменяет состояния объекта.
2. Невозможно получить полную информацию
Слайд 31Идея использовать квантовые объекты для защиты информации от подделки и несанкционированного
Спустя 10 лет Беннет и Брассард, которые были знакомы с работой Вейснера, предложили использовать квантовые объекты для передачи секретного ключа. В 1984 г. они опубликовали статью, в которой описывался протокол квантового распространения ключа ВВ84.
Слайд 381989 г. В Уотсоновском исследовательском центре IBM Чарльзом Беннетом, Джилом Брасардом
24.07.2009 Исследователи из Университета Женевы (University of Geneva) в Швейцарии и Corning Inc. продемонстрировали новый QKD-прототип, который может распределять квантовые ключи на расстоянии 250 км в лабораторных условиях.
20.04. 2010 Создана рекордно быстрая система распространения квантовых ключей со скоростью, превышающей 1 Мбит/с.
Экспериментальная реализация







![ШифрованиеСообщение М шифруется так:Выбирается случайное секретное число k из отрезка [1, p-2]. Вычисляется a =](/img/tmb/2/182425/13ce93081751810f8e2a99c276997240-800x.jpg)