Арксинус, арккосинус, арктангенс, арккотангенс презентация

Содержание

1. Арксинус, арккосинус, арктангенс, арккотангенс
2. Сведения из истории Современные обозначения arcsin и
3. Сведения из истории Общепринятыми эти символы
4. Арксинус Обозначение. Арксинус а обозначается
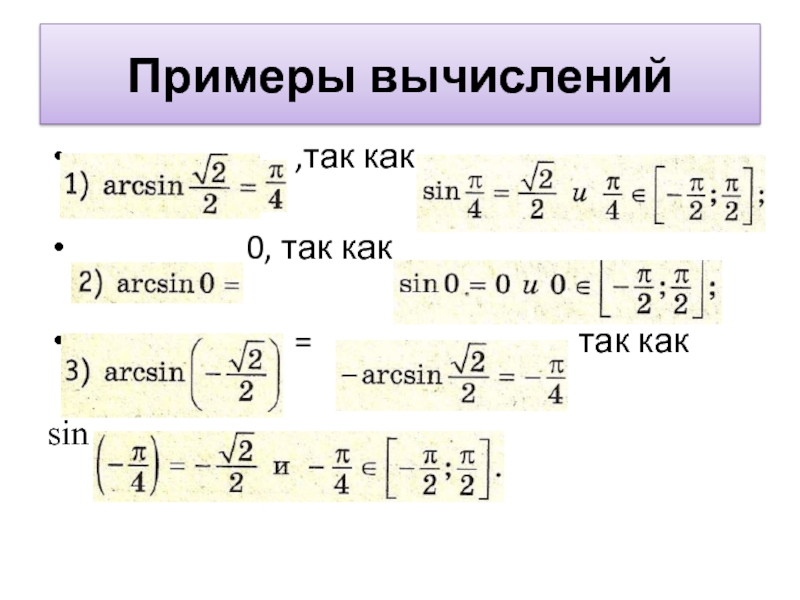
5. Примеры вычислений
6. Арккосинус Обозначение: Арккосинус а обозначается arccosa. Арккосинусом
7. Примеры вычислений 1) 2) 3) 4)
8. Арктангенс Обозначение: Арктангенс а обозначается arctga. Арктангенсом
9. Примеры вычислений 1) 2)
10. Арккотангенс Обозначение: Арккотангенс а обозначается arcсtg a.
11. Примеры вычислений 1) 2)
12. arcsina, arccosa, arctga,acctga-обратные тригонометрические функции Функция
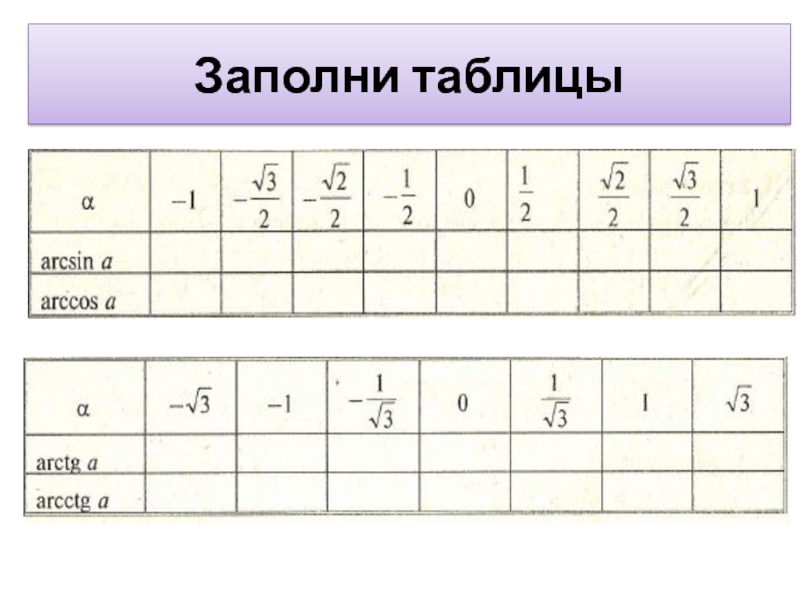
13. Заполни таблицы
14. Самостоятельная работа Вычислить: 1) 2) 3)

Сведения из истории Современные обозначения arcsin и arctg появляются в 1772г.в работах венского математика Щерфера и известного французского ученого

Главная
Математика
Арксинус, арккосинус, арктангенс, арккотангенс

Слайд 1Арксинус, Арккосинус, Арктангенс, Арккотангенс

Слайд 2Сведения из истории
Современные обозначения arcsin и
arctg появляются в 1772г.в работах

венского математика Щерфера и
известного французского ученого
Ж.Л. Лагранжа, хотя
несколько ранее уже
рассматривал Д. Бернулли,
который употреблял иную
символику.

Слайд 3Сведения из истории
Общепринятыми эти символы
стали лишь в конце XVIII
столетия.

Приставка «арк»
происходит от латинского
arcus (лук, дуга), что вполне
согласуется со смыслом
понятия; arcsin х,
например,— это угол (а можно сказать, и дуга),синус которого равен х.

Слайд 4 Арксинус
Обозначение. Арксинус а обозначается arcsina.
Арксинусом числа а называется такое число
из

отрезка , синус которого равен а.
Очевидно, что а є [-1;1].
Т.к

Функция y=arcsin x- нечетная,
поэтому

Слайд 5Примеры вычислений

,так как
0, так как
= , так как
sin

Слайд 6Арккосинус
Обозначение: Арккосинус а обозначается arccosa.
Арккосинусом числа а называется такое число из

отрезка , косинус которого равен а.
Очевидно, что а є [-1; 1]
Т.к.

Функция y=arccosx- четная,
поэтому

Слайд 7Примеры вычислений
1)
2)
3)
4)

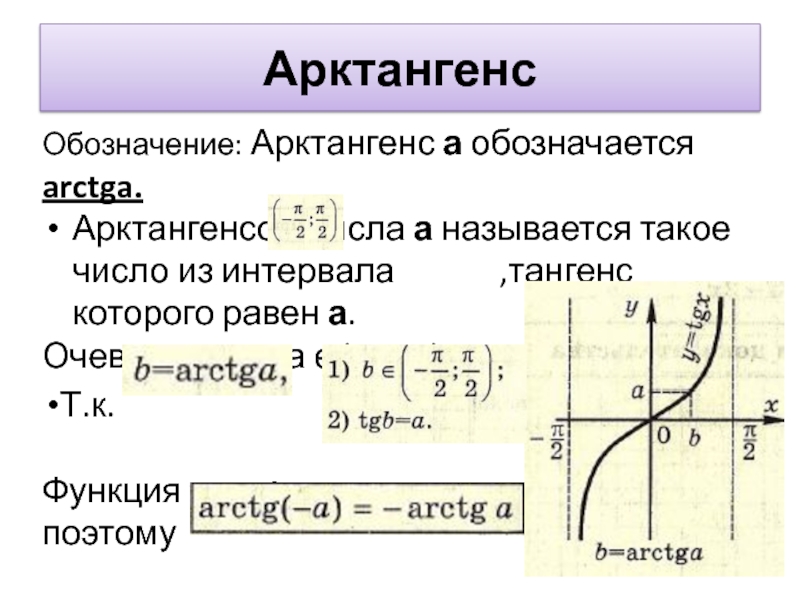
Слайд 8Арктангенс
Обозначение: Арктангенс а обозначается arctga.
Арктангенсом числа а называется такое число из

интервала ,тангенс которого равен а.
Очевидно, что а є (-∞; ∞)
Т.к.

Функция y=arctgx-нечетная,
поэтому

Слайд 9Примеры вычислений
1)
2)

Слайд 10Арккотангенс
Обозначение: Арккотангенс а обозначается arcсtg a.
Арккотангенсом числа а называется такое число из интервала

(0;?),котангенс которого равен а.
Очевидно, что а є (-∞; ∞)
Т.к.

Функция y=arcctgx-нечетная,
поэтому

Слайд 11Примеры вычислений
1)
2)

Слайд 12arcsina, arccosa, arctga,acctga-обратные тригонометрические функции
Функция

обратная функции
Функция обратная функции
Функция обратная функции
Функция обратная функции

Слайд 13Заполни таблицы

Слайд 14Самостоятельная работа
Вычислить:
1)
2)
3)

Скачать презентацию

Арксинус, арккосинус, арктангенс, арккотангенс презентация

Содержание

Слайд 1Арксинус, Арккосинус, Арктангенс, Арккотангенс

Слайд 2Сведения из истории
Современные обозначения arcsin и
arctg появляются в 1772г.в работах

Слайд 3Сведения из истории
Общепринятыми эти символы
стали лишь в конце XVIII
столетия.

Слайд 4 Арксинус
Обозначение. Арксинус а обозначается arcsina.
Арксинусом числа а называется такое число
из

Слайд 5Примеры вычислений

Слайд 6Арккосинус
Обозначение: Арккосинус а обозначается arccosa.
Арккосинусом числа а называется такое число из

Слайд 7Примеры вычислений
1)
2)
3)
4)

Слайд 8Арктангенс
Обозначение: Арктангенс а обозначается arctga.
Арктангенсом числа а называется такое число из

Слайд 9Примеры вычислений
1)
2)

Слайд 10Арккотангенс
Обозначение: Арккотангенс а обозначается arcсtg a.
Арккотангенсом числа а называется такое число из интервала

Слайд 11Примеры вычислений
1)
2)

Слайд 12arcsina, arccosa, arctga,acctga-обратные тригонометрические функции
Функция

Слайд 13Заполни таблицы

Слайд 14Самостоятельная работа
Вычислить:
1)
2)
3)

Обратная связь

Что такое ThePresentation.ru?

Арксинус, арккосинус, арктангенс, арккотангенс презентация

Содержание

Слайд 1Арксинус, Арккосинус, Арктангенс, Арккотангенс

Слайд 2Сведения из историиСовременные обозначения arcsin и arctg появляются в 1772г.в работах

Слайд 3Сведения из историиОбщепринятыми эти символы стали лишь в конце XVIII столетия.

Слайд 4 Арксинус Обозначение. Арксинус а обозначается arcsina.Арксинусом числа а называется такое число из

Слайд 5Примеры вычислений

Слайд 6АрккосинусОбозначение: Арккосинус а обозначается arccosa.Арккосинусом числа а называется такое число из

Слайд 7Примеры вычислений1)2)3)4)

Слайд 8АрктангенсОбозначение: Арктангенс а обозначается arctga.Арктангенсом числа а называется такое число из

Слайд 9Примеры вычислений1)2)

Слайд 10АрккотангенсОбозначение: Арккотангенс а обозначается arcсtg a.Арккотангенсом числа а называется такое число из интервала

Слайд 11Примеры вычислений1)2)

Слайд 12arcsina, arccosa, arctga,acctga-обратные тригонометрические функцииФункция

Слайд 13Заполни таблицы

Слайд 14Самостоятельная работаВычислить:1)2)3)

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 2Сведения из истории
Современные обозначения arcsin и
arctg появляются в 1772г.в работах

Слайд 3Сведения из истории
Общепринятыми эти символы
стали лишь в конце XVIII
столетия.

Слайд 4 Арксинус
Обозначение. Арксинус а обозначается arcsina.
Арксинусом числа а называется такое число
из

Слайд 6Арккосинус
Обозначение: Арккосинус а обозначается arccosa.
Арккосинусом числа а называется такое число из

Слайд 7Примеры вычислений
1)
2)
3)
4)

Слайд 8Арктангенс
Обозначение: Арктангенс а обозначается arctga.
Арктангенсом числа а называется такое число из

Слайд 9Примеры вычислений
1)
2)

Слайд 10Арккотангенс
Обозначение: Арккотангенс а обозначается arcсtg a.
Арккотангенсом числа а называется такое число из интервала

Слайд 11Примеры вычислений
1)
2)

Слайд 12arcsina, arccosa, arctga,acctga-обратные тригонометрические функции
Функция

Слайд 14Самостоятельная работа
Вычислить:
1)
2)
3)