- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы и действия над ними презентация
Содержание
- 1. Векторы и действия над ними
- 2. Обозначается: 3.1. ВЕКТОРЫ НА ПЛОСКОСТИ И
- 3. Обозначается: Длиной или модулем вектора называется расстояние
- 4. В любой системе отсчета вектор характеризуется своими
- 6. Длина вектора определяется по формуле:
- 7. Пусть два вектора заданы своими координатами: Если
- 8. Суммой двух векторов будет вектор, координаты которого равны суммам соответствующих координат исходных векторов.
- 9. Для построения суммы векторов, нужно совместить конец
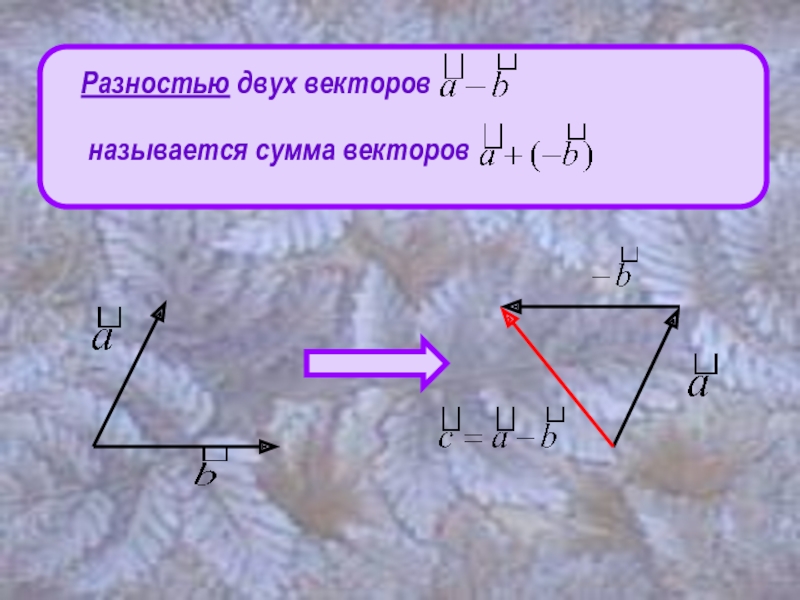
- 10. Разностью двух векторов называется сумма векторов
- 11. В параллелограмме, построенном на двух векторах, одна
- 12. Произведением вектора на число будет вектор,
- 13. Геометрически смысл умножения вектора на число
- 14. Свойства операций сложения и умножения вектора на число 1 2
- 15. 3 4 5
- 16. Скалярным произведением двух векторов называется число,
- 17. Если два вектора заданы своими координатами: То
- 18. Если два вектора перпендикулярны, то их скалярное
Обозначается: 3.1. ВЕКТОРЫ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ Направленный отрезок, на котором заданы начало, конец и направление, называется вектором.
Слайд 2Обозначается:
3.1. ВЕКТОРЫ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
Направленный отрезок, на котором
заданы начало,
конец и направление,
называется вектором.
называется вектором.
Слайд 3Обозначается:
Длиной или модулем вектора называется
расстояние между его началом и концом.
Векторы, лежащие
на одной прямой или
на параллельных прямых, называются
коллинеарными.
на параллельных прямых, называются
коллинеарными.
Если начало и конец вектора совпадают,
то вектор называется нулевым.
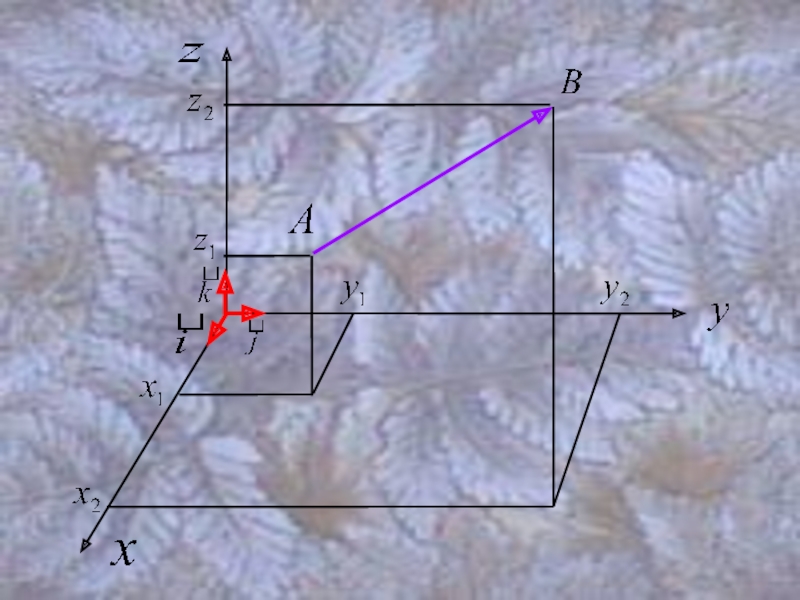
Слайд 4В любой системе отсчета вектор характеризуется своими координатами.
Пусть в системе отсчета
XYZ заданы координаты начала и конца вектора:
Тогда координаты вектора будут:
Где:
Или:
Слайд 7Пусть два вектора заданы своими координатами:
Если эти вектора коллинеарны, то их
соответствующие координаты должны быть пропорциональны:
Условие коллинеарности векторов
Слайд 8Суммой двух векторов будет вектор,
координаты которого равны суммам
соответствующих координат
исходных
векторов.
векторов.
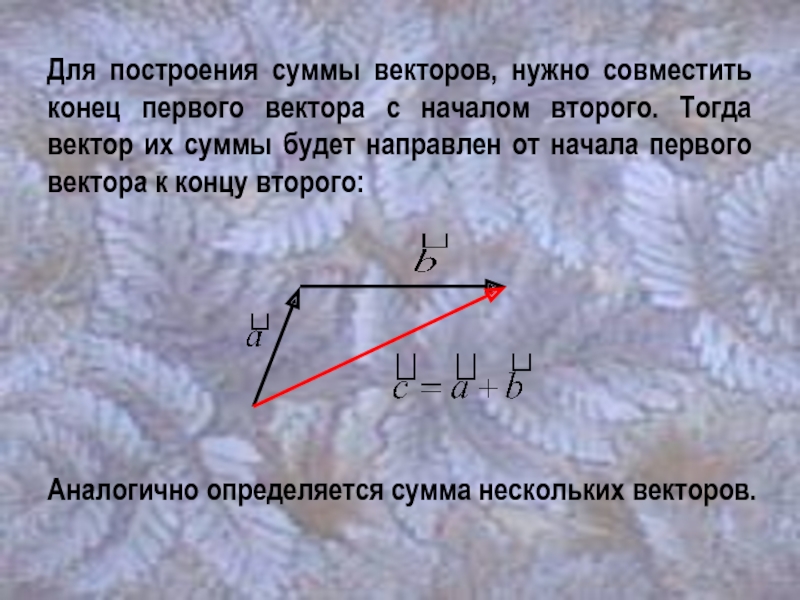
Слайд 9Для построения суммы векторов, нужно совместить конец первого вектора с началом
второго. Тогда вектор их суммы будет направлен от начала первого вектора к концу второго:
Аналогично определяется сумма нескольких векторов.
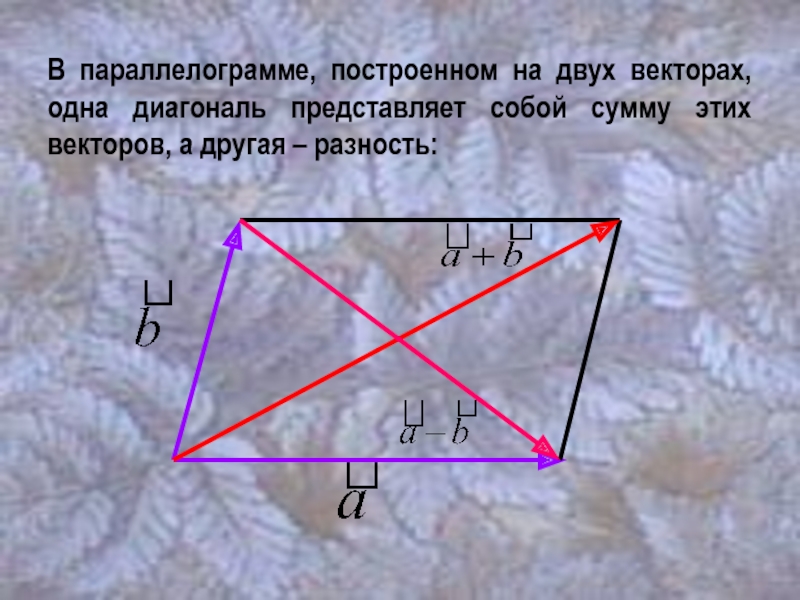
Слайд 11В параллелограмме, построенном на двух векторах, одна диагональ представляет собой сумму
этих векторов, а другая – разность:
Слайд 12Произведением вектора на число будет
вектор, координаты которого равны
произведению соответствующих
координат исходного вектора на это
число.
Слайд 13Геометрически смысл умножения вектора
на число заключается в увеличении его
длины
в λ раз, если lλl>1, и в ее сокращении
во столько же раз при lλl<1.
во столько же раз при lλl<1.
Слайд 16Скалярным произведением двух
векторов называется число, равное
произведению длин этих векторов
на
косинус угла между ними.
косинус угла между ними.
Слайд 17Если два вектора заданы своими координатами:
То скалярное произведение выразится следующим образом:
Отсюда
можно выразить угол между двумя векторами:
Слайд 18Если два вектора перпендикулярны, то их скалярное произведение должно быть равно
нулю:
Условие перпендикулярности
векторов
