- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Анализ выбросов. Диаграммы размахов презентация
Содержание
- 1. Анализ выбросов. Диаграммы размахов
- 2. Диаграммы размахов (ящичковые диаграммы, диаграммы с усами)
- 3. Применение boxplot() Рассмотрим данные, полученные в ходе
- 4. Результат Как видим, количество насекомых на растениях,
- 5. Диаграммы Кливленда Точечные диаграммы Кливленда представляют собой
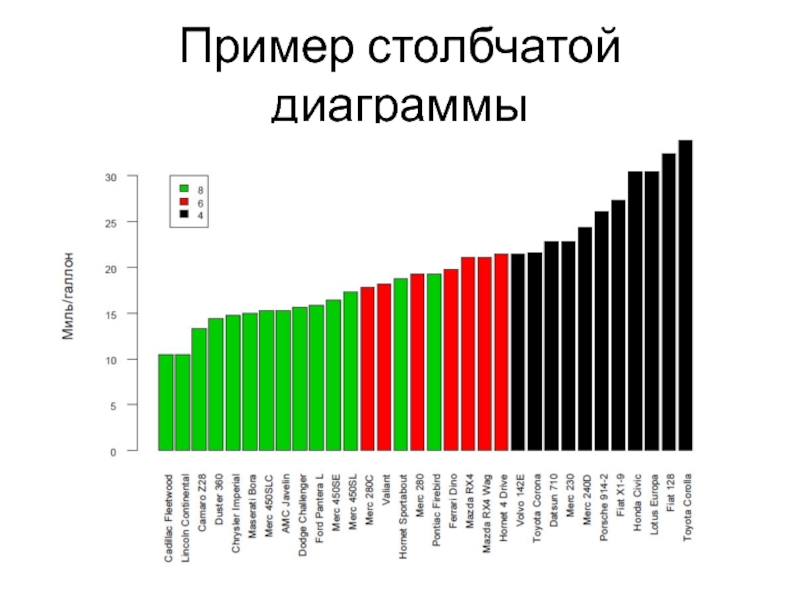
- 6. Пример столбчатой диаграммы
- 7. Точечная диаграмма dotchart(mtcars$mpg, labels = row.names(mtcars), main="Экономия
- 8. Результат Картина станет гораздо более ясной, если
- 9. Подготовка данных Отсортируем исходную таблицу по возрастанию
- 10. Результат
- 11. Выбросы Под "выбросом" мы будем понимать наблюдение,
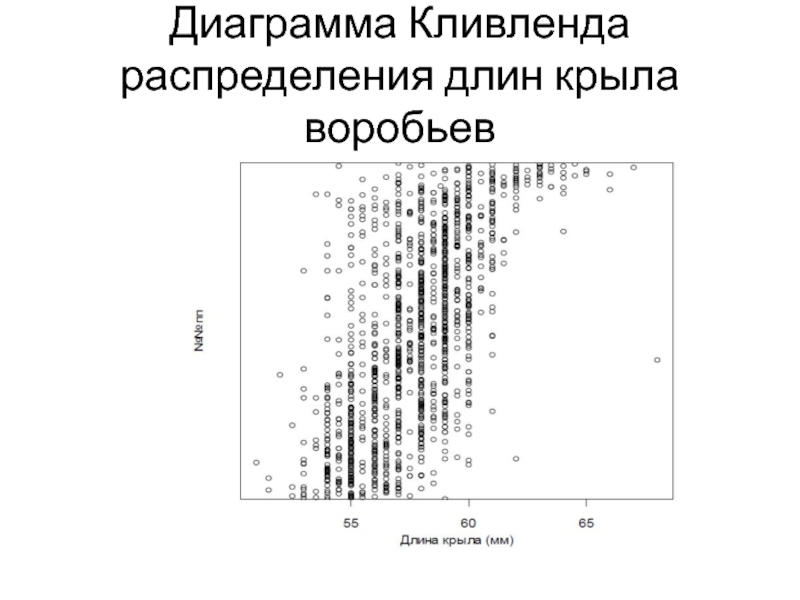
- 12. Диаграмма Кливленда распределения длин крыла воробьев
- 13. Интерпретация результатов На рисунке хорошо выделяется точка,
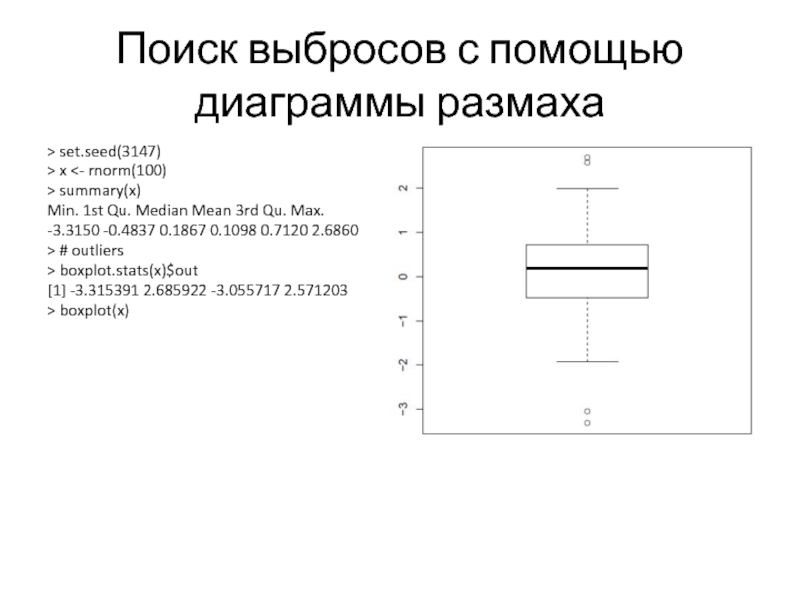
- 14. Поиск выбросов с помощью диаграммы размаха >
- 15. Поиск выбросов с помощью диаграммы размаха >
- 16. Поиск выбросов с помощью диаграммы размаха >
- 17. Результат
- 18. Поиск выбросов > # outliers in either
- 19. Удаление выбросов Более строгий подход к определению
- 20. Нормализующее преобразование Альтернативой удалению необычных значений предиктора
- 21. Пример Проанализируем уровень зараженности двустворчатого моллюска Dreissena
- 22. Пример Моллюски
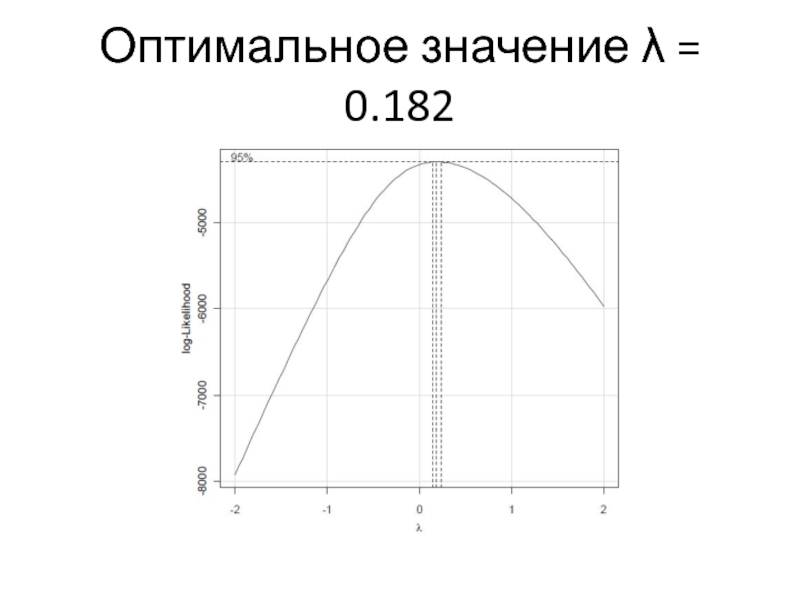
- 23. Оптимальное значение λ = 0.182
- 24. Эффект преобразования CAnumber по методу Бокса-Кокса После
- 25. Тест Граббса С использованием теста Граббса можно
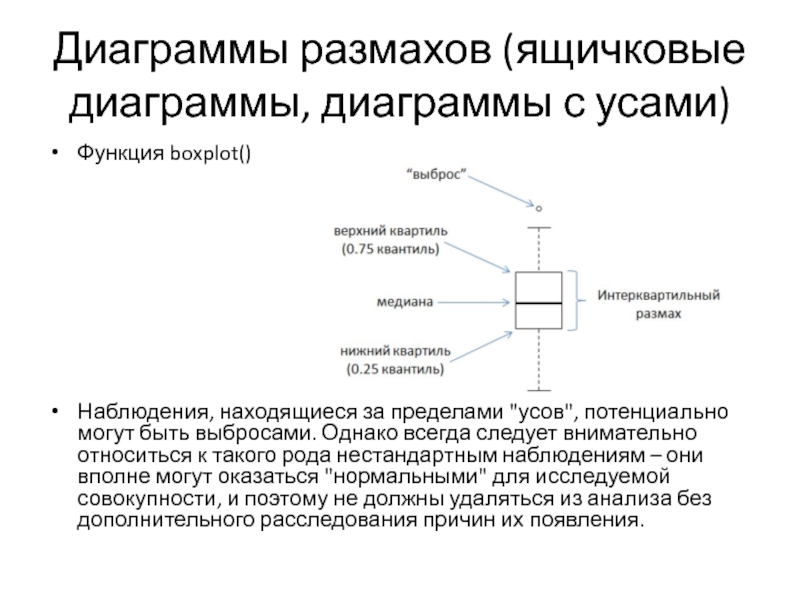
Слайд 2Диаграммы размахов (ящичковые диаграммы, диаграммы с усами)
Функция boxplot()
Наблюдения, находящиеся за пределами
"усов", потенциально могут быть выбросами. Однако всегда следует внимательно относиться к такого рода нестандартным наблюдениям – они вполне могут оказаться "нормальными" для исследуемой совокупности, и поэтому не должны удаляться из анализа без дополнительного расследования причин их появления.
Слайд 3Применение boxplot()
Рассмотрим данные, полученные в ходе эксперимента по изучению эффективности шести
видов инсектицидных средств. Каждым из этих средств обработали по 12 растений, после чего подсчитали количество выживших на растениях насекомых. Данные этого эксперимента входят в состав стандартного набора данных R и доступны по команде data(InsectSprays). В таблице InsectSprays имеется два столбца: count, содержащий результаты подсчета насекомых, и spray, содержащий коды инсектицидных средств (от А до F).
Для построения графика, на котором будут представлены "ящики с усами" для каждого инсектицида, достаточно выполнить команду
boxplot(count ~ spray, data = InsectSprays)
Улучшим график
boxplot(count ~ spray, xlab = "Инсектициды", ylab = "Количество выживших насекомых", main = "Эффективность инсектицидов", col = "coral", data = InsectSprays)
Для построения графика, на котором будут представлены "ящики с усами" для каждого инсектицида, достаточно выполнить команду
boxplot(count ~ spray, data = InsectSprays)
Улучшим график
boxplot(count ~ spray, xlab = "Инсектициды", ylab = "Количество выживших насекомых", main = "Эффективность инсектицидов", col = "coral", data = InsectSprays)
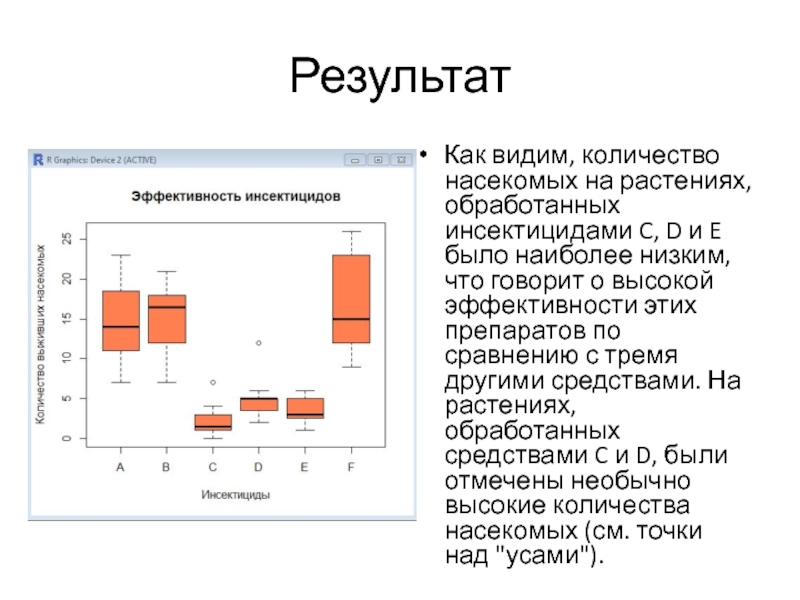
Слайд 4Результат
Как видим, количество насекомых на растениях, обработанных инсектицидами C, D и
E было наиболее низким, что говорит о высокой эффективности этих препаратов по сравнению с тремя другими средствами. На растениях, обработанных средствами C и D, были отмечены необычно высокие количества насекомых (см. точки над "усами").
Слайд 5Диаграммы Кливленда
Точечные диаграммы Кливленда представляют собой графики, на которых точки используются
для отображения значений некоторой количественной переменной (или переменных), разбитых на группы в соответствии с уровнями некоторой номинальной переменной (или переменных). Считается, что такие диаграммы визуально лучше воспринимаются.
Построим столбиковую диаграмму, изображающую распределение 32 моделей автомобилей 1973-1974 годов выпуска по экономичности двигателя (выражается как количество миль, которое автомобиль проезжает на одном галлоне топлива). Данные, использованные для построения диаграммы, были опубликованы в американском журнале Motor Trend в 1974 г. и входят в стандартный набор данных R (доступны по команде data(mtcars)).
Построим столбиковую диаграмму, изображающую распределение 32 моделей автомобилей 1973-1974 годов выпуска по экономичности двигателя (выражается как количество миль, которое автомобиль проезжает на одном галлоне топлива). Данные, использованные для построения диаграммы, были опубликованы в американском журнале Motor Trend в 1974 г. и входят в стандартный набор данных R (доступны по команде data(mtcars)).
Слайд 7Точечная диаграмма
dotchart(mtcars$mpg, labels = row.names(mtcars), main="Экономия топлива у 32 моделей автомобилей",
xlab="Миль/галлон", cex = 0.8)
Параметры функции dotchart():
а) переменная, для которой строится график (mtcars$mpg);
б) текстовый вектор, содержащий названия моделей автомобилей (в данном случае они являются названиями строк таблицы – row.names(mtcars));
в) заголовок графика (аргумент main) и название оси X (аргумент xlab);
г) размер точек на графике и одновременно размер шрифта для названий моделей (cex = 0.8).
Параметры функции dotchart():
а) переменная, для которой строится график (mtcars$mpg);
б) текстовый вектор, содержащий названия моделей автомобилей (в данном случае они являются названиями строк таблицы – row.names(mtcars));
в) заголовок графика (аргумент main) и название оси X (аргумент xlab);
г) размер точек на графике и одновременно размер шрифта для названий моделей (cex = 0.8).
Слайд 8Результат
Картина станет гораздо более ясной, если мы отсортируем данные по возрастанию
пробега, сгруппируем данные по количеству цилиндров в двигателе и раскрасим соответствующие группы разными цветами.
Слайд 9Подготовка данных
Отсортируем исходную таблицу по возрастанию mpg с использованием функции order())
и сохраним результат в виде новой таблицы данных с именем x:
x <- mtcars[order(mtcars$mpg), ]
Создадим новый столбец color в таблице x, который будет содержать числовые коды цветов для каждой из трех групп автомобилей:
x$color[x$cyl==4] <- 1
x$color[x$cyl==6] <- 2
x$color[x$cyl==8] <- 3
Теперь у нас есть все необходимое для построения желаемого графика:
dotchart(x$mpg, labels = row.names(x), groups = x$cyl, gcolor = "blue", pch = 16, main="Экономичность двигателя у 32 моделей автомобилей", xlab="Миль/галлон", cex = 0.8, color = x$color)
x <- mtcars[order(mtcars$mpg), ]
Создадим новый столбец color в таблице x, который будет содержать числовые коды цветов для каждой из трех групп автомобилей:
x$color[x$cyl==4] <- 1
x$color[x$cyl==6] <- 2
x$color[x$cyl==8] <- 3
Теперь у нас есть все необходимое для построения желаемого графика:
dotchart(x$mpg, labels = row.names(x), groups = x$cyl, gcolor = "blue", pch = 16, main="Экономичность двигателя у 32 моделей автомобилей", xlab="Миль/галлон", cex = 0.8, color = x$color)
Слайд 11Выбросы
Под "выбросом" мы будем понимать наблюдение, которое "слишком" велико или "слишком"
мало по сравнению с большинством других имеющихся наблюдений.
Обычно для выявления выбросов используют диаграмму размахов или точечную диаграмму Кливленда.
Например, на следующей диаграмме Кливленда, представлены данные о длине крыла у 1295 воробьев. Здесь таблица была предварительно упорядочена в соответствии с весом птиц, и поэтому облако точек имеет примерно S-образную форму.
Обычно для выявления выбросов используют диаграмму размахов или точечную диаграмму Кливленда.
Например, на следующей диаграмме Кливленда, представлены данные о длине крыла у 1295 воробьев. Здесь таблица была предварительно упорядочена в соответствии с весом птиц, и поэтому облако точек имеет примерно S-образную форму.
Слайд 13Интерпретация результатов
На рисунке хорошо выделяется точка, соответствующая длине крыла 68 мм.
Однако это значение длины крыла не следует рассматривать в качестве выброса, поскольку оно лишь незначительно отличается от других значений длины. Эта точка выделяется на общем фоне лишь потому, что исходные значения длины крыла были упорядочены по весу птиц. Соответственно, выброс скорее стоит искать среди значений веса (т.е. очень высокое значение длины крыла (68 мм) было отмечено у воробья, необычно мало весящего для этого).
Слайд 14Поиск выбросов с помощью диаграммы размаха
> set.seed(3147)
> x summary(x)
Min.
1st Qu. Median Mean 3rd Qu. Max.
-3.3150 -0.4837 0.1867 0.1098 0.7120 2.6860
> # outliers
> boxplot.stats(x)$out
[1] -3.315391 2.685922 -3.055717 2.571203
> boxplot(x)
-3.3150 -0.4837 0.1867 0.1098 0.7120 2.6860
> # outliers
> boxplot.stats(x)$out
[1] -3.315391 2.685922 -3.055717 2.571203
> boxplot(x)
Слайд 15Поиск выбросов с помощью диаграммы размаха
> y df
data.frame(x, y)
> rm(x, y)
> head(df)
x y
1 -3.31539150 0.7619774
2 -0.04765067 -0.6404403
3 0.69720806 0.7645655
4 0.35979073 0.3131930
5 0.18644193 0.1709528
6 0.27493834 -0.8441813
> rm(x, y)
> head(df)
x y
1 -3.31539150 0.7619774
2 -0.04765067 -0.6404403
3 0.69720806 0.7645655
4 0.35979073 0.3131930
5 0.18644193 0.1709528
6 0.27493834 -0.8441813
Слайд 16Поиск выбросов с помощью диаграммы размаха
> attach(df)
> # find the index
of outliers from x
> (a <- which(x %in% boxplot.stats(x)$out))
[1] 1 33 64 74
> # find the index of outliers from y
> (b <- which(y %in% boxplot.stats(y)$out))
[1] 24 25 49 64 74
> detach(df)
> # outliers in both x and y
> (outlier.list1 <- intersect(a,b))
[1] 64 74
> plot(df)
> points(df[outlier.list1,], col="red", pch="+", cex=2.5)
> (a <- which(x %in% boxplot.stats(x)$out))
[1] 1 33 64 74
> # find the index of outliers from y
> (b <- which(y %in% boxplot.stats(y)$out))
[1] 24 25 49 64 74
> detach(df)
> # outliers in both x and y
> (outlier.list1 <- intersect(a,b))
[1] 64 74
> plot(df)
> points(df[outlier.list1,], col="red", pch="+", cex=2.5)
Слайд 18Поиск выбросов
> # outliers in either x or y
> (outlier.list2
union(a,b))
[1] 1 33 64 74 24 25 49
> plot(df)
> points(df[outlier.list2,], col="blue", pch="x“, cex=2)
[1] 1 33 64 74 24 25 49
> plot(df)
> points(df[outlier.list2,], col="blue", pch="x“, cex=2)
Слайд 19Удаление выбросов
Более строгий подход к определению выбросов состоит в оценке того,
какое влияние эти необычные наблюдения оказывают на результаты анализа. При этом следует делать различие между необычными наблюдениями для зависимых и независимых переменных (предикторов). Например, при изучении зависимости численности какого-либо биологического вида от температуры большинство значений температуры может лежать в пределах от 15 до 20 °С, и лишь одно значение может оказаться равным 25 °С. Такой план эксперимента, мягко говоря, неидеален, поскольку диапазон температур от 20 до 25 °С будет исследован неравномерно. Однако при проведении реальных полевых исследований возможность выполнить измерения для высокой температуры может представиться только однажды. Что же тогда делать с этим необычным измерением, выполненным при 25 °С? При большом объеме наблюдений подобные редкие наблюдения можно исключить из анализа. Однако при относительно небольшом объеме данных еще большее его уменьшение может быть нежелательным с точки зрения статистической значимости получаемых результатов.
Слайд 20Нормализующее преобразование
Альтернативой удалению необычных значений предиктора является нормализующее преобразование (чаще всего,
логарифмирование). В общем случае, найти оптимальное решение позволяет так называемое преобразование Бокса-Кокса.
Универсальное семейство преобразований Бокса-Кокса (БК) случайной величины x является степенным преобразованием с произвольным положительным или отрицательным показателем степени λ. Поскольку деление на нуль приводит к неопределенности, то при λ = 0 используется логарифмическое преобразование x’(λ) = ln(x). Найти значение λ можно, например, найдя максимум логарифма функции максимального правдоподобия.
Универсальное семейство преобразований Бокса-Кокса (БК) случайной величины x является степенным преобразованием с произвольным положительным или отрицательным показателем степени λ. Поскольку деление на нуль приводит к неопределенности, то при λ = 0 используется логарифмическое преобразование x’(λ) = ln(x). Найти значение λ можно, например, найдя максимум логарифма функции максимального правдоподобия.
Слайд 21Пример
Проанализируем уровень зараженности двустворчатого моллюска Dreissena polymorpha инфузорией Conchophthirus acuminatus в
трех озерах Беларуси. Данные возьмем с сайта figshare. В таблице данных нас будут интересовать две переменные: длина раковины моллюска (ZMlength, мм) и число обнаруженных в моллюске инфузорий (CAnumber).
Слайд 22Пример
Моллюски
графика
# изменения параметра БК-трансформации для заданной модели
m.null <- lm(Моллюски$CAnumber+1~1)
bc.null <- boxCox(m.null)
bc.null.opt <- bc.null$x[which.max(bc.null$y)]
paste("Оптимальная лямбда БК-преобразования:",bc.null.opt)
[1] "Оптимальная лямбда БК-преобразования: 0.181818181818182"
CAnumber_bc <- bcPower(Моллюски$CAnumber+1, bc.null.opt)
par(mfrow=c(2,1))
boxplot(Моллюски$CAnumber,horizontal = TRUE,col = "steelblue",
xlab = "Численность инфузорий (экз)")
boxplot(CAnumber_bc,horizontal = TRUE,col = "coral",
xlab = "Численность инфузорий (БК-преобразование)")
# изменения параметра БК-трансформации для заданной модели
m.null <- lm(Моллюски$CAnumber+1~1)
bc.null <- boxCox(m.null)
bc.null.opt <- bc.null$x[which.max(bc.null$y)]
paste("Оптимальная лямбда БК-преобразования:",bc.null.opt)
[1] "Оптимальная лямбда БК-преобразования: 0.181818181818182"
CAnumber_bc <- bcPower(Моллюски$CAnumber+1, bc.null.opt)
par(mfrow=c(2,1))
boxplot(Моллюски$CAnumber,horizontal = TRUE,col = "steelblue",
xlab = "Численность инфузорий (экз)")
boxplot(CAnumber_bc,horizontal = TRUE,col = "coral",
xlab = "Численность инфузорий (БК-преобразование)")
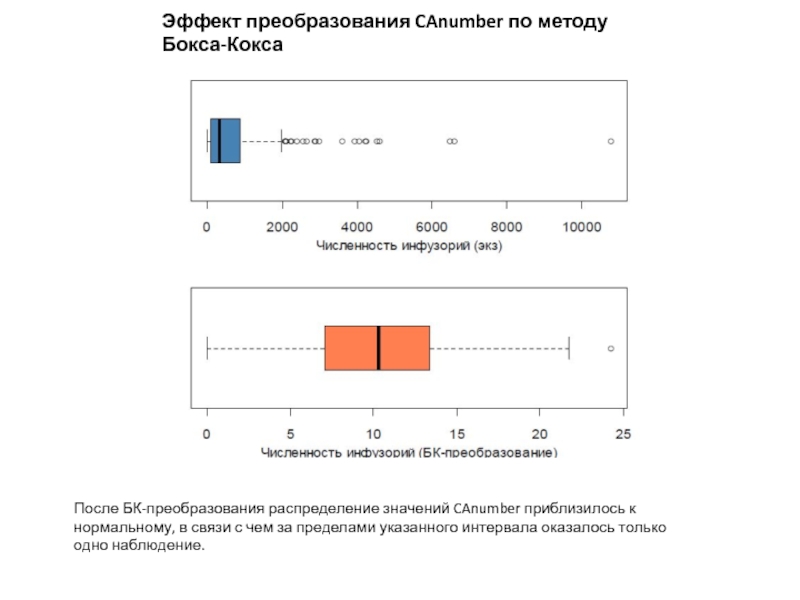
Слайд 24Эффект преобразования CAnumber по методу Бокса-Кокса
После БК-преобразования распределение значений CAnumber приблизилось
к нормальному, в связи с чем за пределами указанного интервала оказалось только одно наблюдение.
Слайд 25Тест Граббса
С использованием теста Граббса можно проверить нулевую гипотезу о том,
что максимальное значение не является выбросом:
library(outliers)
grubbs.test(Моллюски$CAnumber, type = 10)
Grubbs test for one outlier
data: Моллюски$CAnumber
G = 10.8336, U = 0.7524, p-value < 2.2e-16
alternative hypothesis: highest value 10782 is an outlier
grubbs.test(CAnumber_bc, type = 10)
Grubbs test for one outlier
data: CAnumber_bc
G = 3.3267, U = 0.9767, p-value = 0.1961
alternative hypothesis: highest value 24.2569 is an outlier
library(outliers)
grubbs.test(Моллюски$CAnumber, type = 10)
Grubbs test for one outlier
data: Моллюски$CAnumber
G = 10.8336, U = 0.7524, p-value < 2.2e-16
alternative hypothesis: highest value 10782 is an outlier
grubbs.test(CAnumber_bc, type = 10)
Grubbs test for one outlier
data: CAnumber_bc
G = 3.3267, U = 0.9767, p-value = 0.1961
alternative hypothesis: highest value 24.2569 is an outlier












![Поиск выбросов> # outliers in either x or y> (outlier.list2 plot(df)> points(df[outlier.list2,], col=](/img/tmb/5/461802/f46bef1e28152ed9b1f393eb0787211a-800x.jpg)