- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численный анализ нелинейных моделей и теория Куна-Таккера (Лекция 5) презентация
Содержание
- 1. Численный анализ нелинейных моделей и теория Куна-Таккера (Лекция 5)
- 2. СОДЕРЖАНИЕ Текущий контроль Методы наискорейшего спуска (спуск по градиенту) Элементы теории Куна-Таккера
- 3. ТЕКУЩИЙ КОНТРОЛЬ 1 Выбрать оптимальную архитектуру обсерватории,
- 4. ТЕКУЩИЙ КОНТРОЛЬ 2 РЕШИТЬ МЕТОДОМ МНОЖИТЕЛЕЙ ЛАГРАНЖА i-порядковый номер студента.
- 5. ПОСТАНОВКА ЗАДАЧИ Задана нелинейная однокритериальная оптимизационная модель
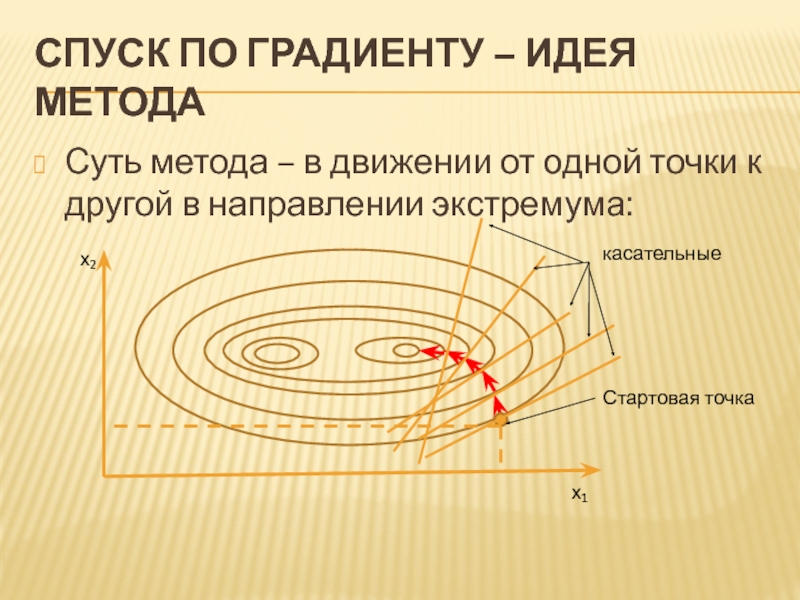
- 6. СПУСК ПО ГРАДИЕНТУ – ИДЕЯ МЕТОДА Суть
- 7. АЛГОРИТМ СПУСКА ПО ГРАДИЕНТУ – ПЕРВЫЕ ДВА
- 8. АЛГОРИТМ СПУСКА ПО ГРАДИЕНТУ – СЛЕДУЮЩИЕ ЧЕТЫРЕ
- 9. ПОСЛЕДНИЕ ЧЕТЫРЕ ШАГА АЛГОРИТМА Шаг 7. Старые
- 10. ПРИМЕР 1 Пользуясь спуском по градиенту решить
- 11. РЕШЕНИЕ 1)
- 12. РЕШЕНИЕ – ВТОРАЯ ИТЕРАЦИЯ 2) Ограничения
- 13. РЕШЕНИЕ – ТРЕТЬЯ ИТЕРАЦИЯ 3) Ограничения выполняются, новое значение целевой функции f = 0,888.
- 14. РЕШЕНИЕ – ЧЕТВЕРТАЯ ИТЕРАЦИЯ 4)
- 15. РЕШЕНИЕ – ПЯТАЯ ИТЕРАЦИЯ 5)
- 16. РЕШЕНИЕ – ШЕСТАЯ ИТЕРАЦИЯ 6)
- 17. САМОСТОЯТЕЛЬНО Пользуясь приведенным выше алгоритмом решить задачу
- 18. ОПРЕДЕЛЕНИЕ ВЫПУКЛЫХ ФУНКЦИЙ Функция f называют выпуклой
- 19. ОПРЕДЕЛЕНИЕ ВОГНУТЫХ ФУНКЦИЙ Функция f называют вогнутой
- 20. ОПРЕДЕЛЕНИЯ ГЛОБАЛЬНОГО И ЛОКАЛЬНОГО ОПТИМУМА Функция называется
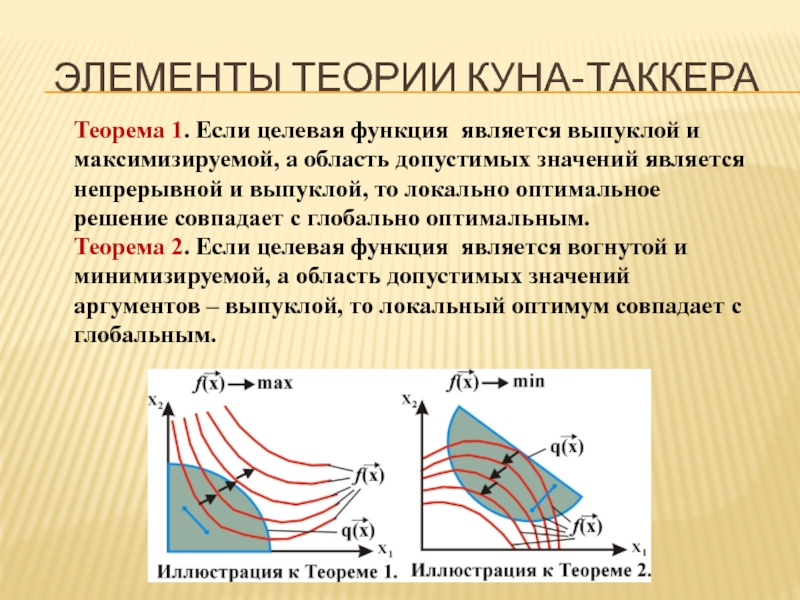
- 21. ЭЛЕМЕНТЫ ТЕОРИИ КУНА-ТАККЕРА Теорема 1. Если целевая
- 22. САМОСТОЯТЕЛЬНО Определить являлись ли решения задач (1)
- 23. ПОИСК ПО ГРАДИЕНТУ С ИЗМЕНЯЕМОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ.
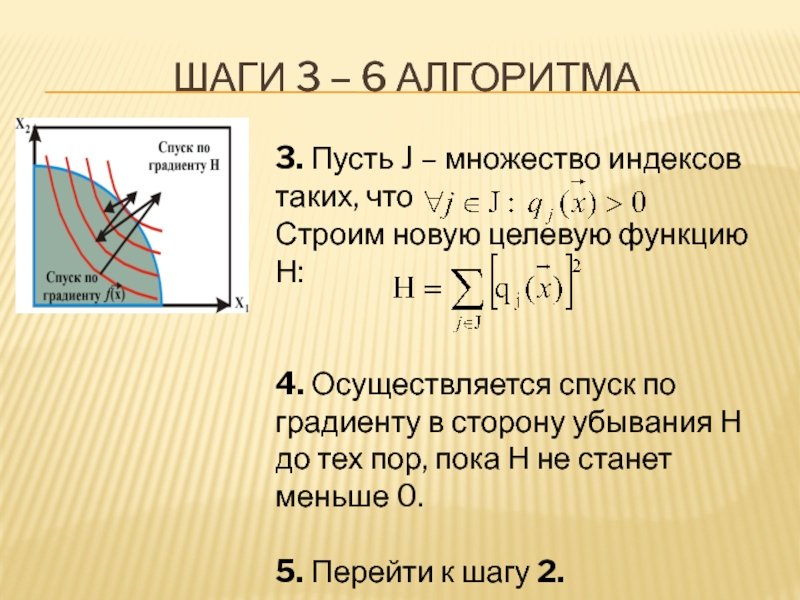
- 24. ШАГИ 3 – 6 АЛГОРИТМА 3. Пусть
- 25. САМОСТОЯТЕЛЬНО Дать формальное описание градиентного поиска с
Слайд 2СОДЕРЖАНИЕ
Текущий контроль
Методы наискорейшего спуска (спуск по градиенту)
Элементы теории Куна-Таккера
Слайд 3ТЕКУЩИЙ КОНТРОЛЬ 1
Выбрать оптимальную архитектуру обсерватории, корпус которой является цилиндрическим, а
h1
d
h2
d/2
Слайд 5ПОСТАНОВКА ЗАДАЧИ
Задана нелинейная однокритериальная оптимизационная модель вида:
Все функции системы (1) являются
Вектора переменных. Требуется определить оптимальный вектор переменных.
Слайд 6СПУСК ПО ГРАДИЕНТУ – ИДЕЯ МЕТОДА
Суть метода – в движении от
х₁
х₂
Стартовая точка
касательные
Слайд 7АЛГОРИТМ СПУСКА ПО ГРАДИЕНТУ – ПЕРВЫЕ ДВА ШАГА (ВСЕГО 10 ШАГОВ)
Шаг 2. Для каждой переменной вычисляется новое значение по формуле:
Слайд 8АЛГОРИТМ СПУСКА ПО ГРАДИЕНТУ – СЛЕДУЮЩИЕ ЧЕТЫРЕ ШАГА
Шаг 3.
Шаг 4. Если f₁ «лучше» чем f, то перейти к следующему шагу, нет – к шагу 8.
Шаг 5. Если ограничения системы (1) выполняются, то перейти к следующему шагу, в противном случае – к шагу 8.
Шаг 6. Переменной f присваивается значение, равное f₁.
Слайд 9ПОСЛЕДНИЕ ЧЕТЫРЕ ШАГА АЛГОРИТМА
Шаг 7. Старые значения переменных заменяются на новые,
Шаг 8. Величине шага β присваивается новое значение, которое вдвое меньше хранящегося в памяти: β = β/2.
Шаг 9. Если новое значение β больше заданной точности поиска Ɛ, то перейти к шагу 2, в противном случае – к шагу 10.
Шаг 10. Конец алгоритма
Слайд 10ПРИМЕР 1
Пользуясь спуском по градиенту решить задачу:
Точка старта: х=у=3; f=0,66, начальная
Слайд 11РЕШЕНИЕ
1)
z=0,8.
Новые значения переменных удовлетворяют ограничениям, f=0,8, поэтому величина шага β не меняется.
Слайд 12РЕШЕНИЕ – ВТОРАЯ ИТЕРАЦИЯ
2)
Ограничения не выполняются, поэтому величина шага β
Слайд 13РЕШЕНИЕ – ТРЕТЬЯ ИТЕРАЦИЯ
3)
Ограничения выполняются, новое значение целевой функции f =
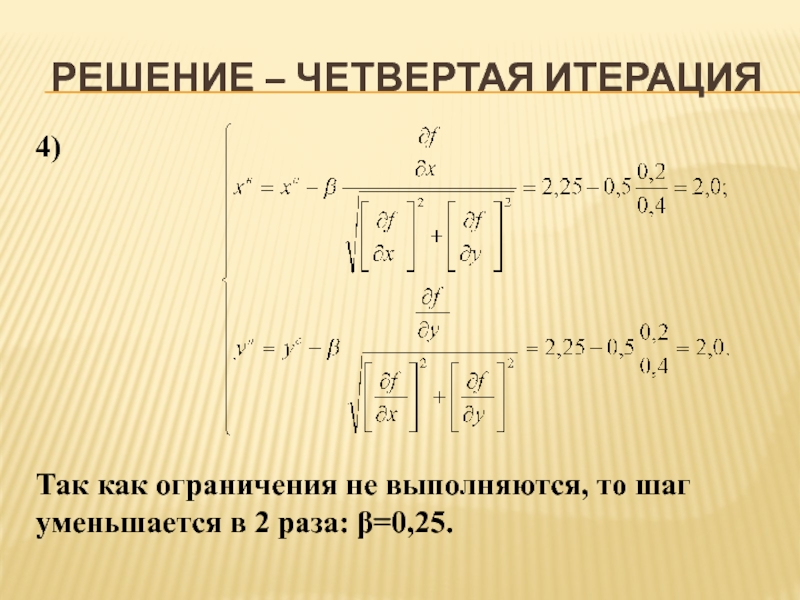
Слайд 14РЕШЕНИЕ – ЧЕТВЕРТАЯ ИТЕРАЦИЯ
4)
Так как ограничения не выполняются, то шаг уменьшается
Слайд 16РЕШЕНИЕ – ШЕСТАЯ ИТЕРАЦИЯ
6)
Значения переменных не удовлетворяют ограничению, шаг β уменьшается
Слайд 17САМОСТОЯТЕЛЬНО
Пользуясь приведенным выше алгоритмом решить задачу (2):
Решить задачи (1) и (2),
Сформулировать достоинства и недостатки спуска по градиенту.
Слайд 18ОПРЕДЕЛЕНИЕ ВЫПУКЛЫХ ФУНКЦИЙ
Функция f называют выпуклой на интервале [a,b]
a b х
f
Слайд 19ОПРЕДЕЛЕНИЕ ВОГНУТЫХ ФУНКЦИЙ
Функция f называют вогнутой на интервале [a,b]
f
a b x
Слайд 20ОПРЕДЕЛЕНИЯ ГЛОБАЛЬНОГО И ЛОКАЛЬНОГО ОПТИМУМА
Функция называется локально оптимальной в точке «х»
Функция достигает в точке х глобального оптимума, если для любого допустимого вектора y≠x значение функции «хуже», чем в «х».
Слайд 21ЭЛЕМЕНТЫ ТЕОРИИ КУНА-ТАККЕРА
Теорема 1. Если целевая функция является выпуклой и максимизируемой,
Теорема 2. Если целевая функция является вогнутой и минимизируемой, а область допустимых значений аргументов – выпуклой, то локальный оптимум совпадает с глобальным.
Слайд 22САМОСТОЯТЕЛЬНО
Определить являлись ли решения задач (1) и (2), полученные выше спуском
Проверить, являлись ли решения тех же задач, полученные методом множителей Лагранжа, глобально оптимальными.
Слайд 23ПОИСК ПО ГРАДИЕНТУ С ИЗМЕНЯЕМОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ.
1. Определена задача:
Слайд 24ШАГИ 3 – 6 АЛГОРИТМА
3. Пусть J – множество индексов таких,
Строим новую целевую функцию Н:
4. Осуществляется спуск по градиенту в сторону убывания Н до тех пор, пока Н не станет меньше 0.
5. Перейти к шагу 2.
6. Конец алгоритма.
Слайд 25САМОСТОЯТЕЛЬНО
Дать формальное описание градиентного поиска с изменяемой целевой функцией и построить
Пользуясь этим методом, решить задачу:
Реализовать метод программно.
Оценить достоинства и недостатки метода.















![ОПРЕДЕЛЕНИЕ ВЫПУКЛЫХ ФУНКЦИЙФункция f называют выпуклой на интервале [a,b] если для любой точки отрезка, соединяющего](/img/tmb/6/506272/3f3e8f9eea458cd588ce97190c63c27f-800x.jpg)
![ОПРЕДЕЛЕНИЕ ВОГНУТЫХ ФУНКЦИЙФункция f называют вогнутой на интервале [a,b] если для любой точки отрезка, соединяющего](/img/tmb/6/506272/e0f7dd9f73e61b8a1bb665044c4e5431-800x.jpg)