- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ეკონომიკისა და ბიზნესის სტატისტიკა. ცენტრალური ტენდენციის მახასიათებლები. თემა 2 презентация
Содержание
- 1. ეკონომიკისა და ბიზნესის სტატისტიკა. ცენტრალური ტენდენციის მახასიათებლები. თემა 2
- 2. მონაცემთა ტიპები მაგალითები: ქორწინების სტატუსი გაქვთ თუ
- 3. მონაცემთა რაოდენობრივი აღწერა არითმეტ. საშუალო მედიანა მოდა
- 4. ცენტრალური ტენდენციის საზომები ცენტრალური ტენდენცია საშუალო მედიანა
- 5. (არითმეტიკული) საშუალო (Mean) ცენტრალური ტენდენციის ყველაზე ხშირად
- 6. არითმეტიკული საშუალო საშუალო = მნიშვნელობათა ჯამი გაყოფილი
- 7. მედიანა დალაგებულ (ზრდადობით ან კლებადობით) მწკრივში მედიანა
- 8. მედიანის პოვნა
- 9. მოდა ცენტრალური ტენდენციის საზომი ყველაზე ხშირი მოვლენა
- 10. 5 სახლი ზღვის პირას მაგალითი: გამეორება სახლის
- 11. შემაჯამებელი სტატისტიკები საშუალო: ($3,000,000/5)
- 12. ძირითადად გამოიყენება საშუალო, თუ არ არის ამოვარდნილი
- 13. კვარტილები კვარტილები ყოფენ ზრდადობით (კლებადობით) დალაგებულ მონაცემებს
- 14. შეწონილი საშუალო მონაცემთა სიმრავლის შეწონილი საშუალო არის
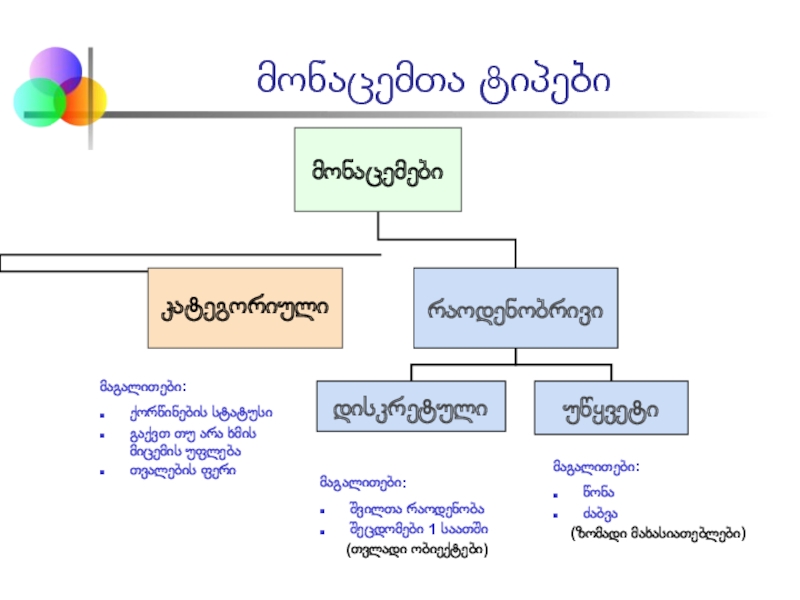
Слайд 2მონაცემთა ტიპები
მაგალითები:
ქორწინების სტატუსი
გაქვთ თუ არა ხმის მიცემის უფლება
თვალების ფერი
მაგალითები:
შვილთა რაოდენობა
შეცდომები 1 საათში
(თვლადი ობიექტები)
მაგალითები:
წონა
ძაბვა
(ზომადი მახასიათებლები)
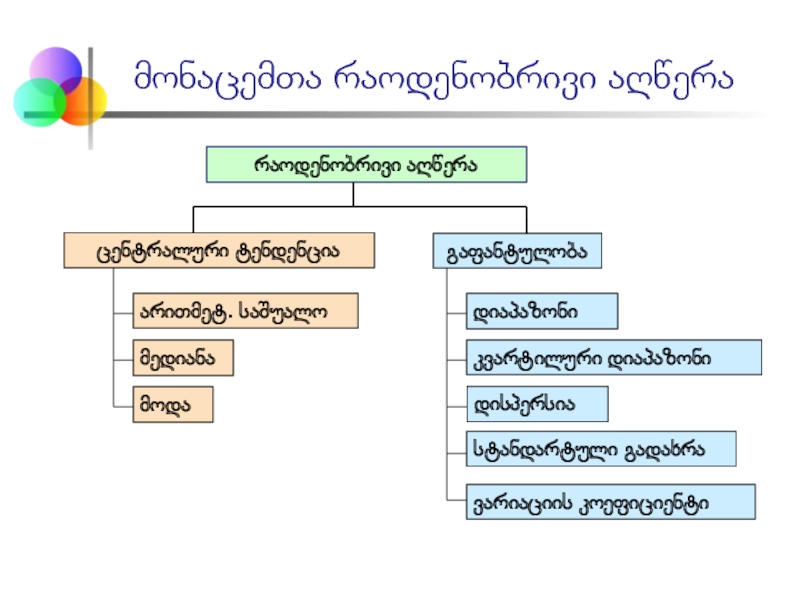
Слайд 3მონაცემთა რაოდენობრივი აღწერა
არითმეტ. საშუალო
მედიანა
მოდა
რაოდენობრივი აღწერა
დისპერსია
სტანდარტული გადახრა
ვარიაციის კოეფიციენტი
დიაპაზონი
კვარტილური დიაპაზონი
ცენტრალური ტენდენცია
გაფანტულობა
Слайд 4ცენტრალური ტენდენციის საზომები
ცენტრალური ტენდენცია
საშუალო
მედიანა
მოდა
დალაგებულ მონაცემთა შუა წერტილი
ყველაზე ხშირი დაკვირვება
არითმეტიკული საშუალო
Слайд 5(არითმეტიკული) საშუალო (Mean)
ცენტრალური ტენდენციის ყველაზე ხშირად გამოყენებადი საზომი
N მნიშვნელობათა პოპულაციისათვის:
n ზომის
შერჩევის ზომა
დაკვირვების ობიექტები
პოპულაციის ზომა
პოპულაციის მნიშვნელობები
Слайд 6არითმეტიკული საშუალო
საშუალო = მნიშვნელობათა ჯამი გაყოფილი მნიშნელობათა რაოდენობაზე
იცვლება ექსტრემალური (ამოვარდნილი) მნიშვნელობების
(გაგრძ.)
0 1 2 3 4 5 6 7 8 9 10
საშუალო= 3
0 1 2 3 4 5 6 7 8 9 10
საშუალო = 4
Слайд 7მედიანა
დალაგებულ (ზრდადობით ან კლებადობით) მწკრივში მედიანა არის “შუა” რიცხვი (50% მის
ხდება ექსტრემალური მნიშვნელობების გავლენის თავიდან აცილება
0 1 2 3 4 5 6 7 8 9 10
Median = 3
0 1 2 3 4 5 6 7 8 9 10
Median = 3
Слайд 8მედიანის პოვნა
თუ რიცხვთა ოდენობა კენტია, მედიანა შუა წერტილია
თუ რიცხვთა ოდენობა ლუწია,
მედიანის მდებარეობა = დალაგებული მონაცემების
-ე წევრი
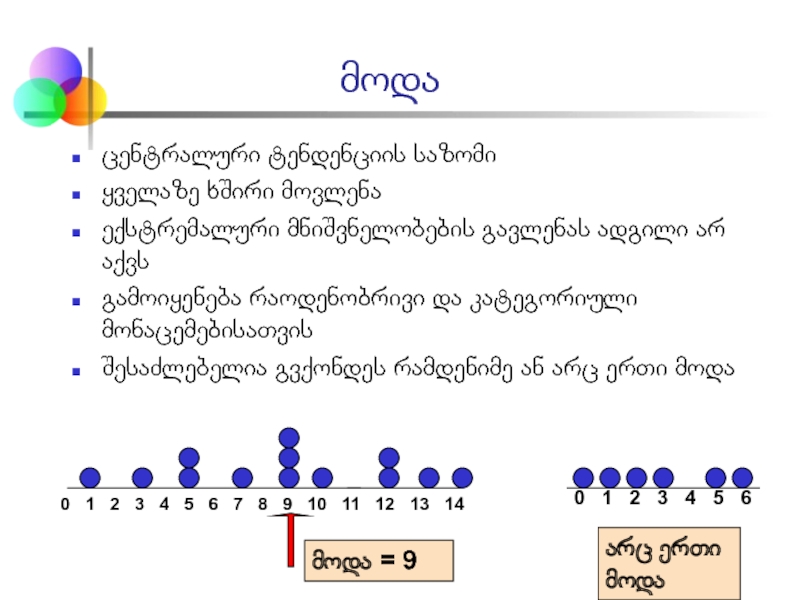
Слайд 9მოდა
ცენტრალური ტენდენციის საზომი
ყველაზე ხშირი მოვლენა
ექსტრემალური მნიშვნელობების გავლენას ადგილი არ აქვს
გამოიყენება რაოდენობრივი
შესაძლებელია გვქონდეს რამდენიმე ან არც ერთი მოდა
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
მოდა = 9
0 1 2 3 4 5 6
არც ერთი მოდა
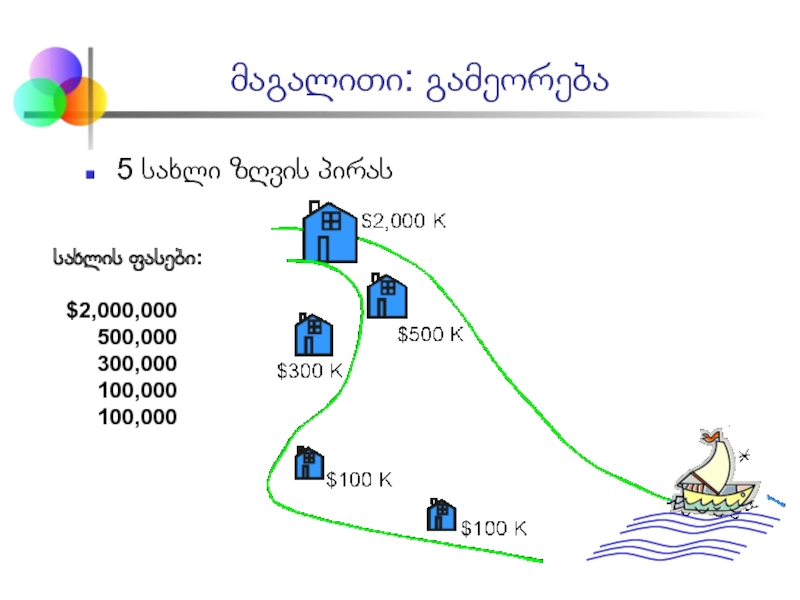
Слайд 105 სახლი ზღვის პირას
მაგალითი: გამეორება
სახლის ფასები:
$2,000,000
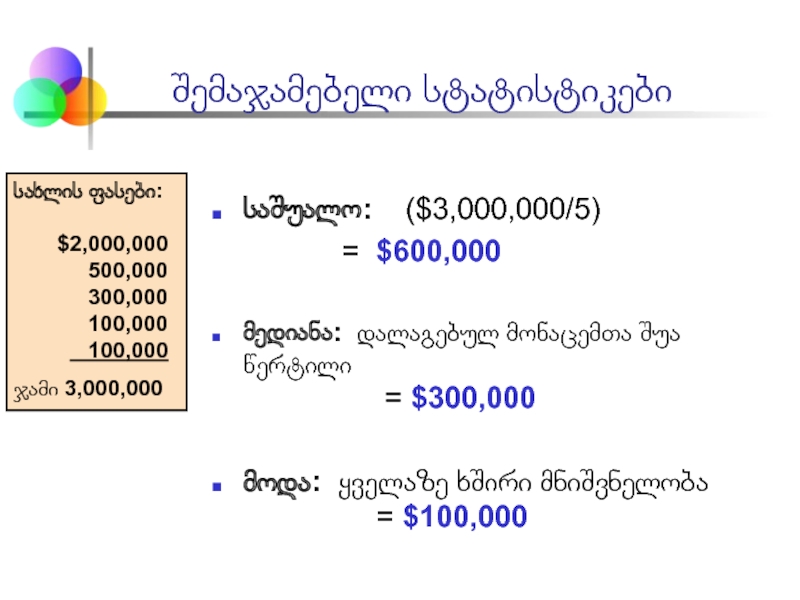
Слайд 11შემაჯამებელი სტატისტიკები
საშუალო: ($3,000,000/5)
= $600,000
მედიანა: დალაგებულ მონაცემთა შუა წერტილი
მოდა: ყველაზე ხშირი მნიშვნელობა = $100,000
სახლის ფასები:
$2,000,000
500,000
300,000
100,000
100,000
ჯამი 3,000,000
Слайд 12ძირითადად გამოიყენება საშუალო, თუ არ არის ამოვარდნილი მნიშვნელობები
ასეთ შემთხვევაში გამოიყენება მედიანა,
მაგალითი: სახლის მედიანური ფასების გამოყენება რეგიონისთვის – ნაკლებად მგრძნობიარე ამოვარდნილი მნიშვნელობების მიმართ
მდებარეობის რომელი საზომია “საუკეთესო”?
Слайд 13კვარტილები
კვარტილები ყოფენ ზრდადობით (კლებადობით) დალაგებულ მონაცემებს 4 სეგმენტად, რომლებიც შეიცავს მნიშნელობათა
25%
პირველი კვარტილი, Q1, არის მნიშვნელობა, რომელზეც დაკვირვებათა 25% უფრო ნაკლებია და 75% – უფრო მეტი.
Q2 არის იგივე რაც მედიანა (50% უფრო ნაკლები, 50% უფრო მეტი)
მესამე კვარტილისთვის (Q3) მხოლოდ დაკვირვებათა 25% არის უფრო მეტი
Q1
Q2
Q3
25%
25%
25%
Слайд 14შეწონილი საშუალო
მონაცემთა სიმრავლის შეწონილი საშუალო არის
სადაც wi არის i–ური დაკვირვების
გამოიყენება, როდესაც მონაცემები უკვე დაჯგუფებულია n კლასად, სადაც i–ურ კლასში მოქცეულია wi ოდენობის მნიშვნელობები