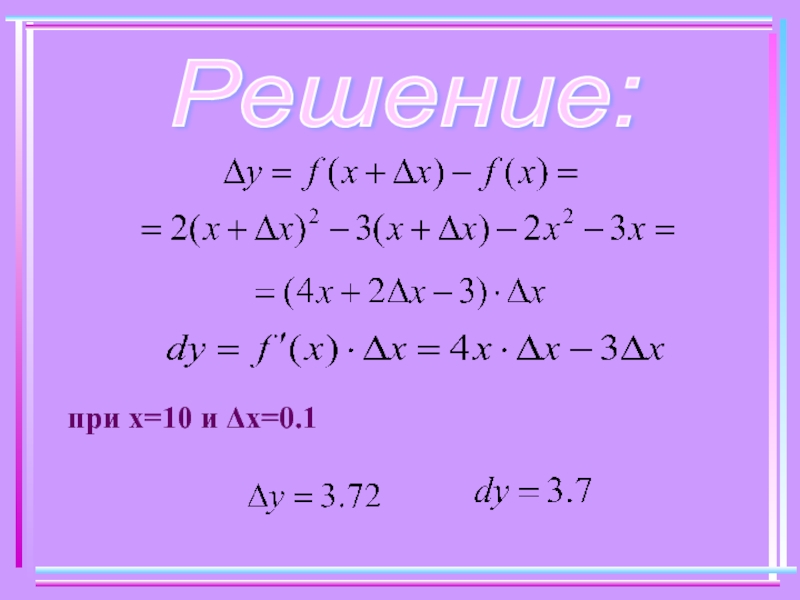- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциал функции презентация
Содержание
- 1. Дифференциал функции
- 2. 10.1. ПОНЯТИЕ ДИФФЕРЕНЦИАЛА ФУНКЦИИ Пусть функция
- 3. Где - бесконечно малая величина при Следовательно,
- 4. Дифференциалом функции называется главная, линейная относительно
- 5. Пример. Найти приращение и дифференциал функции при х=10 и Δх=0.1
- 6. Решение: при х=10 и Δх=0.1
- 7. Пример. Найти дифференциал функции
- 8. Решение: Следовательно, дифференциал независимой переменной равен приращению этой переменной:
Слайд 210.1. ПОНЯТИЕ ДИФФЕРЕНЦИАЛА
ФУНКЦИИ
Пусть функция y=f(x) определена на промежутке Х и
Тогда существует конечная производная
На основании теоремы о связи бесконечно малых величин с пределами функций имеем:
Слайд 3Где
- бесконечно малая величина при
Следовательно,
Таким образом, приращение функции
состоит из двух слагаемых:
1.
2. нелинейного, являющегося бесконечно малой величиной более высокого порядка, чем
Слайд 4Дифференциалом функции называется
главная, линейная относительно Δх, часть
приращения функции, равная произведению
производной
переменной: