მენეჯერული სტატისტიკა. პოპულაციის პარამეტრების შეფასება. თავი 8 презентация

Содержание

Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc. Chap 8- საკითხები: მთავარი საკითხები: განსხვავება წერტილოვანი და ნდობის ინტერვალის შეფასებებს შორის ნდობის ინტერვალის საშუალოს შეფასების განსაზღვრა პოპულაციისთვის

Слайд 1Chap 8-
თავი 8

პოპულაციის პარამეტრების შეფასება
მენეჯერული სტატისტიკა

Слайд 2Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

საკითხები:

მთავარი საკითხები:
განსხვავება წერტილოვანი და ნდობის ინტერვალის შეფასებებს შორის

ნდობის ინტერვალის საშუალოს შეფასების განსაზღვრა პოპულაციისთვის Z და t განაწილებების შემთხვევაში

ნდობის ინტერვალის ფორმირება და შეფასება პოპულაციისთვის

Слайд 3Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ნდობის ინტერვალი

განვიხილავთ:
ნდობის ინტერვალი პოპულაციის საშუალოსთვის, μ
როდესაც პოპულაციის ვარიაცია σ2 ცნობილია
როდესაც პოპულაციის ვარიაცია σ2 არ არის ცნობილი
ნდობის ინტერვალი პოპულაციის პროპორციისთვის, (დიდი შერჩევა)

Слайд 4Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

განმარტებები:

პოპულაციის პარამეტრის შეფასება ხდება „სტატისტიკის“ საშუალებით:
შემთხვევითი სიდიდე, რომელიც განისაზღვრება შერჩევიდან მიღებული მონაცემებით
რომლის მნიშვნელობა არის პარამეტრის (პოპულაციის შეფასების) მიახლოება

შემთხვევითი სიდიდის კონკრეტული მნიშვნელობა არის შეფასება

Слайд 5Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

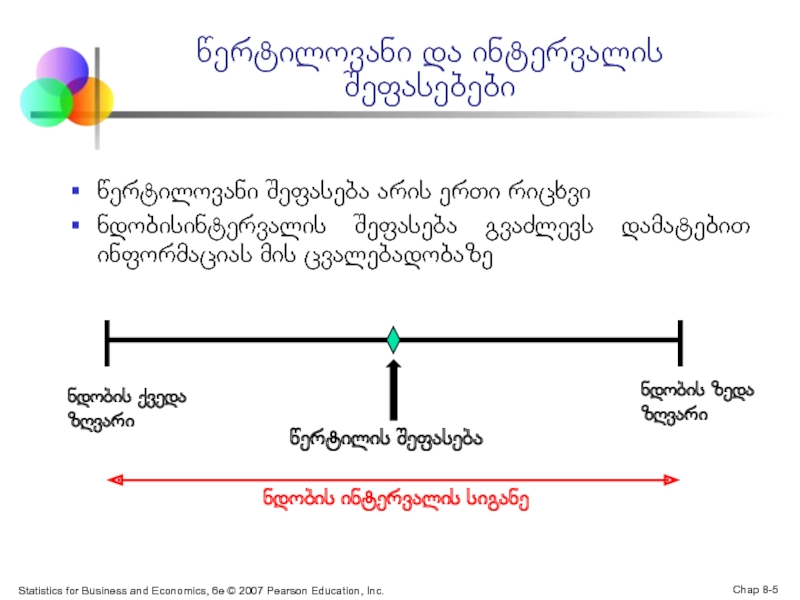
წერტილოვანი და ინტერვალის შეფასებები

წერტილოვანი შეფასება არის ერთი რიცხვი
ნდობისინტერვალის შეფასება გვაძლევს დამატებით ინფორმაციას მის ცვალებადობაზე



წერტილის შეფასება

ნდობის ქვედა ზღვარი

ნდობის ზედა ზღვარი

ნდობის ინტერვალის სიგანე

Слайд 6Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

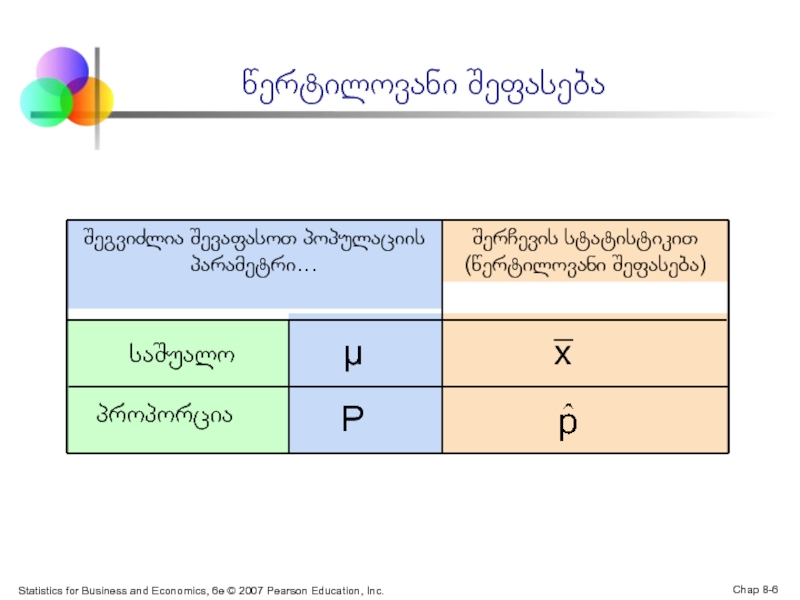
შეგვიძლია შევაფასოთ პოპულაციის პარამეტრი…




წერტილოვანი შეფასება

შერჩევის სტატისტიკით
(წერტილოვანი შეფასება)

საშუალო

პროპორცია

P

x


μ

Слайд 7Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

გადაუადგილებლობა

წერტილოვანი შეფასება არის გადაუადგილებელი შეფასება პარამეტრისა θ, თუ შერჩევიდან მიღებული -ს მოსალოდნელი მნიშვნელობა, ან საშუალო, არის θ,


მაგალითად:
შერჩევის საშუალო არის μ-ს გადაუადგილებელი შეფასება
შერჩევის ვარიაცია არის σ2 -ს გადაუადგილებელი შეფასება
შერჩევის პროპორცია არის P-ს გადაუადგილებელი შეფასება

Слайд 8Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

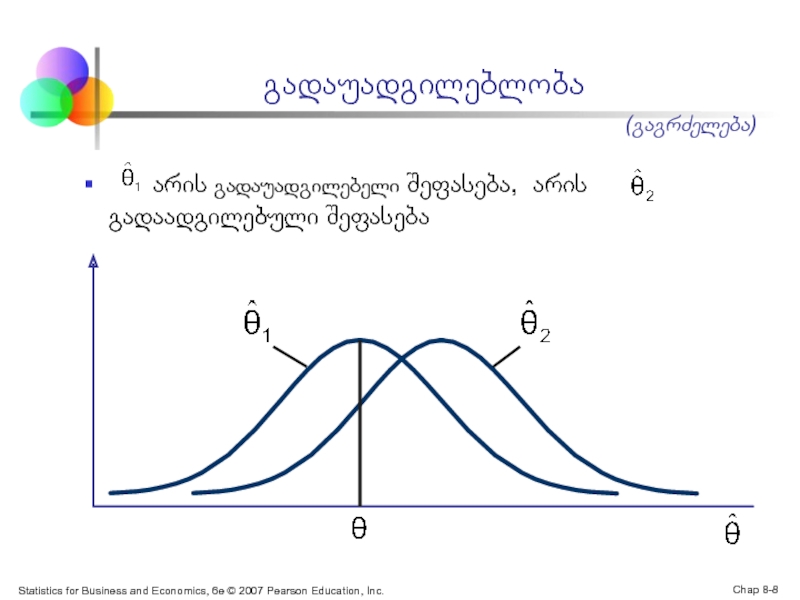
არის გადაუადგილებელი შეფასება, არის გადაადგილებული შეფასება






გადაუადგილებლობა

(გაგრძელება)

Слайд 9Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

გადაადგილება

თუ არის θ-ს შეფასება

-ს გადაადგილება არის მის საშუალოსა და θ-ს შორის სხვაობა



გადაუადგილებელი შეფასების გადაადგილება არის 0

Слайд 10Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ძალმოსილება

თუ არის θ-ს შეფასება

არის θ-ს ძალმოსილი შეფასება, თუ -ს მოსალოდნელი მნიშვნელობისა და θ-ს შორის სხვაობა მცირდება შერჩევის სიდიდის ზრდასთან ერთად.

როდესაც გადაუადგილებელი შეფასების მოპოვება ვერ ხერხდება, სასურველია შეფასება იყოს ძალმოსილი

Слайд 11Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ეფექტური შეფასება

თუ გვაქვს θ-ს რამდენიმე გადაუადგილებელი შეფასება ყველაზე ეფექტური θ-ს შეფასება, ან უმცირესი ვარიაციის მქონე გადაუადგილებელი შეფასება არის გადაუადგილებელი შეფასება უმცირესი ვარიაციით

თუ და არის θ-ს გადაუადგილებელი შეფასებები, რომელიც გამომდინარეობს ერთიდაიმავე სიდიდის მქონე შერჩევიდან, მაშინ

იქნება უფრო მეტად ეფექტური ვიდრე თუ


-ს შედარებითი ეფექტურობა -ს მიმართ არის:


Слайд 12Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ნდობის ინტერვალი

რამდენად არაზუსტი შეიძლება იყოს პოპულაციის პარამეტრის წერტილოვანი შეფასება?

ინტერვალის შეფასება მეტ ინფორმაციას გვაძლევს პოპულაციის მახასიათებლებზე, ვიდრე წერტილოვანი შეფასება

ასეთი ინტერვალის შეფასებებს ვუწოდებთ ნდობით ინტერვალებს

Слайд 13Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ნდობის ინტერვალის შეფასება

ინტერვალი გვაძლევს სხვადასხვა ინფორმაციას:
ითვალისწინებს სხვადასხვა შერჩევების სტატისტიკების ვარიაციას
გვაძლევს ინფორმაციას პოპულაციის უცნობი პარამეტრისა და შეფასებას შორის შესაძლო განსხვავებაზე
წარმოდგენილია სანდოობის დონის მაჩვენებლით
და სანდოობის დონე არასოდეს არის 100%-ს ტოლი

Слайд 14Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ნდობის ინტერვალი და სანდოობის დონე

თუ P(a < θ < b) = 1 - α, a-სა და b-ს შორის ინტერვალი 100(1 - α)% არის θ-ს ნდობის ინტერვალი.

(1 - α)-ს მნიშვნელობა განსაზღვრავს ნდობის ინტერვალს (სადაც α არის 0-სა და 1-ს შორის)

პოპულაციიდან განმეორებითი შერჩევებიდან, ყველა აგებული ინტერვალებიდან, 100(1 - α)% შეიცავს რეალურ პარამეტრს.
ამ მეთოდით დათვლილი ნდობის ინტერვალი სადაც a < θ < b არის 100(1 - α)%

Слайд 15Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

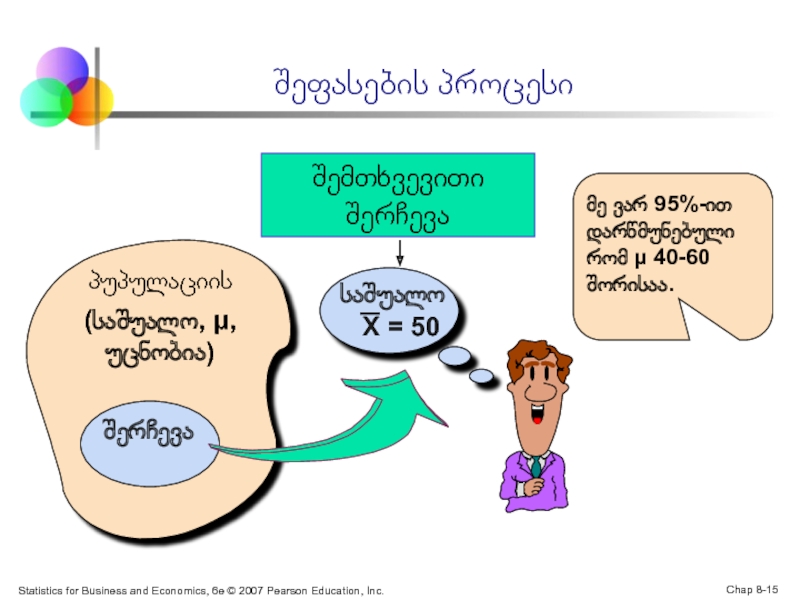
შეფასების პროცესი


(საშუალო, μ, უცნობია)

პუპულაციის

შემთხვევითი შერჩევა



საშუალო
X = 50



შერჩევა

Слайд 16Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

სანდოობის დონე, (1-α)

თუ სანდოობის დონე = 95%
ანუ (1 - α) = 0.95
შედარებითი სიხშირის ინტერპრეტაცია:
განმეორებითი შერჩევებიდან, ყველა აგებული ნდობის ინტერვალებიდან, 95% შეიცავს რეალურ პარამეტრს.
კონკრეტული ინტერვალი შეიცავს ან არ შეიცავს რეალურ პარამეტრს
კონკრეტულ ინტერვალში რეალური პარამეტრის ალბათობა არ არის გაანალიზებული

(continued)

Слайд 17Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ზოგადი ფორმულა

ყველა ნდობის ინტერვალისთვის ზოგადი ფორმულა არის:



ნდობის ფაქტორის მნიშვნელობა დამოკიდებულია სანდოობის დონეზე

წერტილის შეფასება ± (ნდობის ფაქტორი)(სტანდარტული გადახრა)

Слайд 18Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

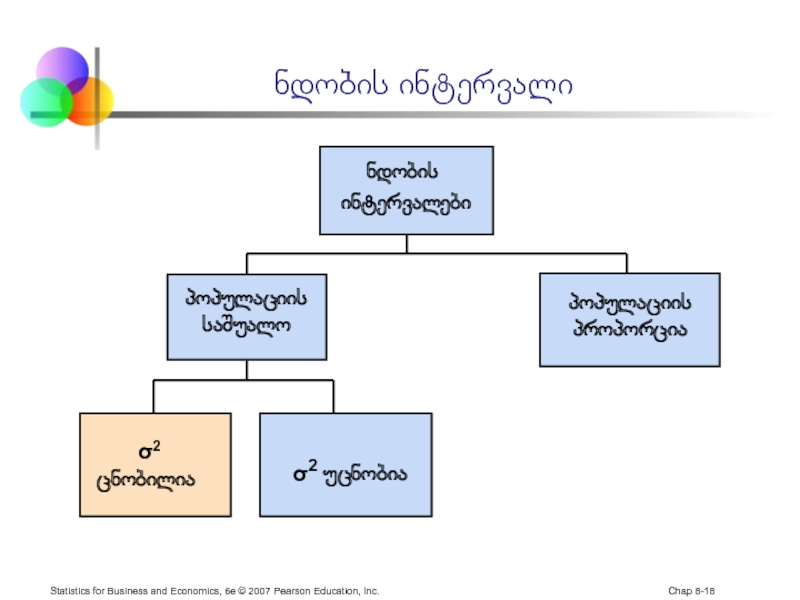
ნდობის ინტერვალი


პოპულაციის
საშუალო


σ2 უცნობია


ნდობის

ინტერვალები


პოპულაციის პროპორცია


σ2
ცნობილია


Слайд 19Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ნდობის ინტერვალი μ-სთვის (σ2 ცნობილია)

დაშვება
პოპულაციის ვარიაცია σ2 ცნობილია
პოპულაცია- ნორმალური განაწილება
თუ პოპულაცია ნორმალურია, ავიღოთ დიდი ზომის შერჩევა
ნდობის ინტერვალის შეფასება :



(სადაც zα/2 არის ნორმ. განაწილების მნიშვნელობა სადაც ალბათობა არის α/2, ორმხრივი)

Слайд 20Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ცდომილების ზღვარი (ME)

ნდობის ინტერვალი,





ასევე:
სადაც ME არის ცდომილების ზღვარი (margin of error)



ინტერვალის სიგანე, w, არის ორჯერ ცდომილების ზღვარი

Слайд 21Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ცდომილების ზღვარის შემცირება

ცდომილების ზღვარი შეიძლება შემცირდეს თუ:
თუ პოპულაციის სტანდარტული გადახრა შეიძლება შემცირდეს (σ↓)

თუ შერჩევის სიდიდე გაიზრდება (n↑)

თუ სანდოობის დონე შემცირდება, (1 – α) ↓

Слайд 22Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-


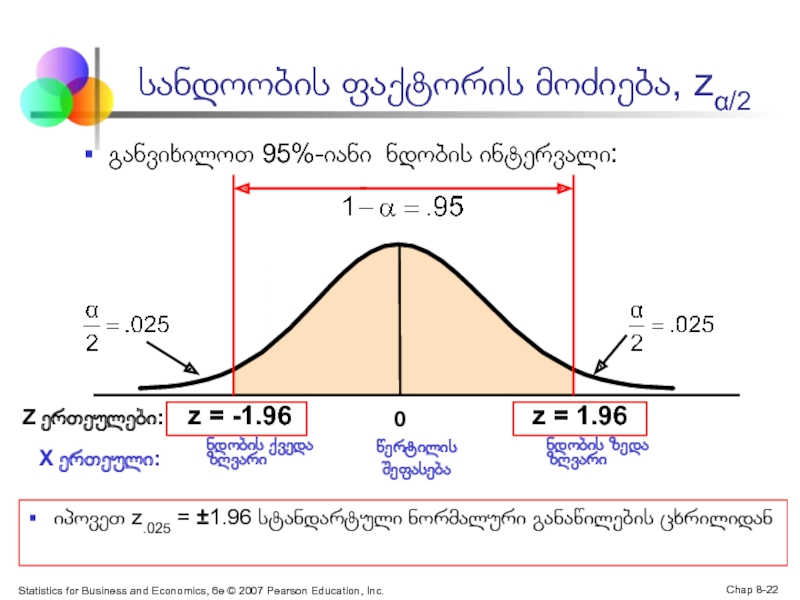
სანდოობის ფაქტორის მოძიება, zα/2

განვიხილოთ 95%-იანი ნდობის ინტერვალი:





z = -1.96

z = 1.96

ნდობის ქვედა ზღვარი

ნდობის ზედა ზღვარი

Z ერთეულები:

X ერთეული:

წერტილის შეფასება

0



იპოვეთ z.025 = ±1.96 სტანდარტული ნორმალური განაწილების ცხრილიდან

Слайд 23Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-


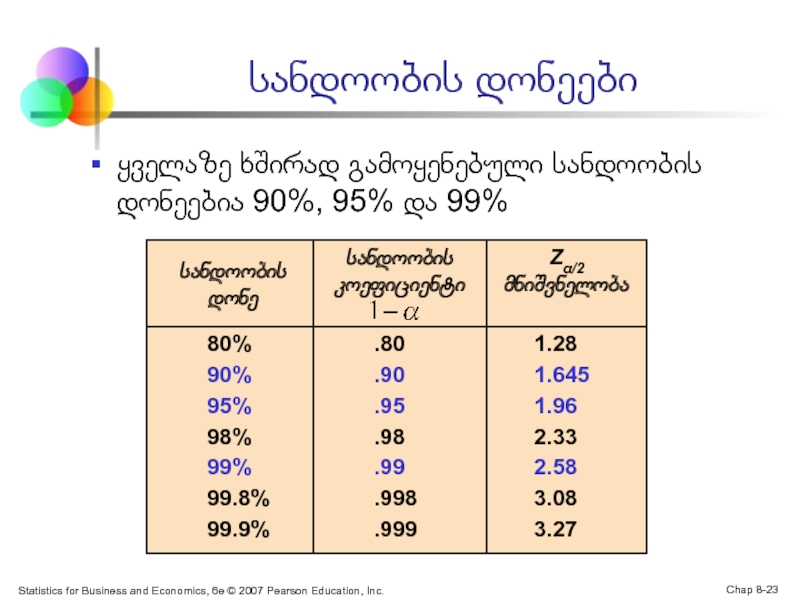
სანდოობის დონეები

ყველაზე ხშირად გამოყენებული სანდოობის დონეებია 90%, 95% და 99%

სანდოობის დონე

სანდოობის კოეფიციენტი

Zα/2 მნიშვნელობა

1.28
1.645
1.96
2.33
2.58
3.08
3.27

.80
.90
.95
.98
.99
.998
.999

80%
90%
95%
98%
99%
99.8%
99.9%

Слайд 24Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-




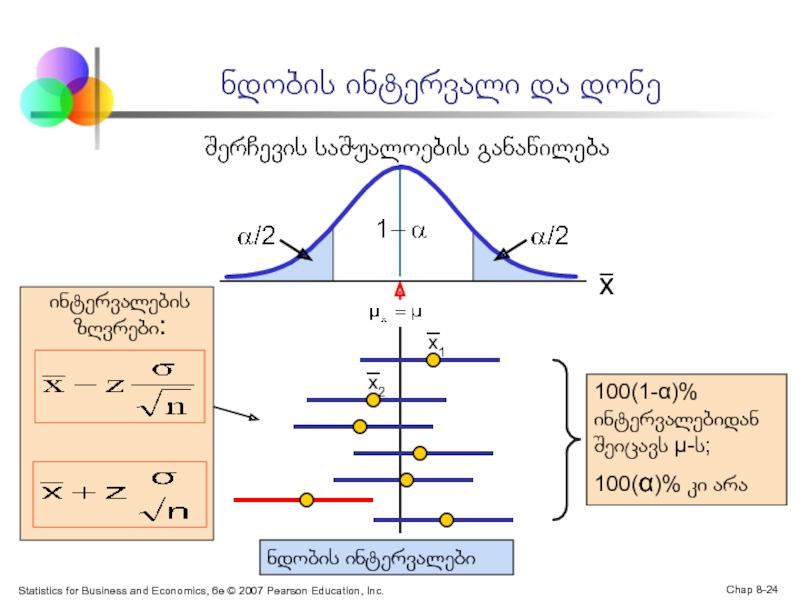
ნდობის ინტერვალი და დონე

ნდობის ინტერვალები

ინტერვალების ზღვრები:


100(1-α)% ინტერვალებიდან შეიცავს μ-ს;
100(α)% კი არა



შერჩევის საშუალოების განაწილება


x

x1


x2







Слайд 25Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

მაგალითი

შერჩეული 11 სქემა დიდი პოპულაციიდან ხასიათდება 2.20 ohms გამძლეობით. წინა ტესტირებებიდან ვიცით, რომ სტანდარტული გადახრა არის 0.35 ohms.

განსაზღვრეთ 95%-იანი ნდობის ინტერვალი პოპულაციის საშუალო გამძლეობისთვის

Слайд 26Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-


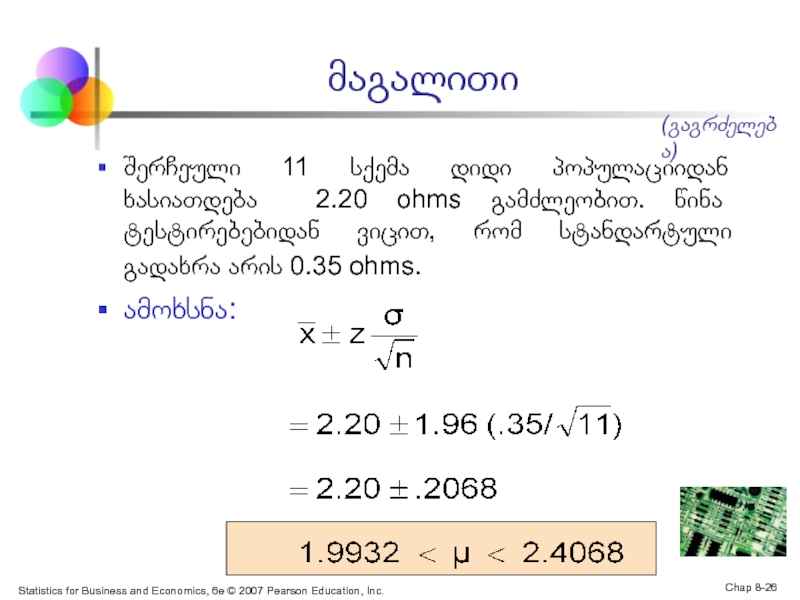
მაგალითი

შერჩეული 11 სქემა დიდი პოპულაციიდან ხასიათდება 2.20 ohms გამძლეობით. წინა ტესტირებებიდან ვიცით, რომ სტანდარტული გადახრა არის 0.35 ohms.
ამოხსნა:

(გაგრძელება)

Слайд 27Statistics for Business and Economics, 6e © 2007 Pearson Education, Inc.
Chap

8-

ინტერპრეტაცია

ჩვენ 95%-ით დარწმუნებულნი ვართ, რომ რეალურად საშუალო გამძლეობა არის 1.9932-სა და 2.4068 ohms შორის.
მიუხედავად იმისა, რომ რეალური საშუალო შეიძლება იყოს ან არ იყოს ამ ინტერვალში, ყველა ინტერვალის 95%-ში (რომელიც ამ გზით მივიღეთ) შეიცავს რეალურ საშუალოს

Похожие презентации

aktivizatsiya poznavatelnoy deyatelnosti mladshikh shkolnikov 280
Лекция 8. Минимизация. Элементы математической логики и теории автоматов (продолжение) 394
umnodenie na chislo 100 254
Фокусы в математике 988
Иррациональные числа. История открытия 540
Исследование функций методами дифференциального исчисления. Условие постоянства функции 396

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика