- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЗОЛОТОЕ СЕЧЕНИЕ презентация
Содержание
- 1. ЗОЛОТОЕ СЕЧЕНИЕ
- 2. Цель данной работы: изучить геометрическое определение
- 3. Содержание Понятие золотого сечения Основатели
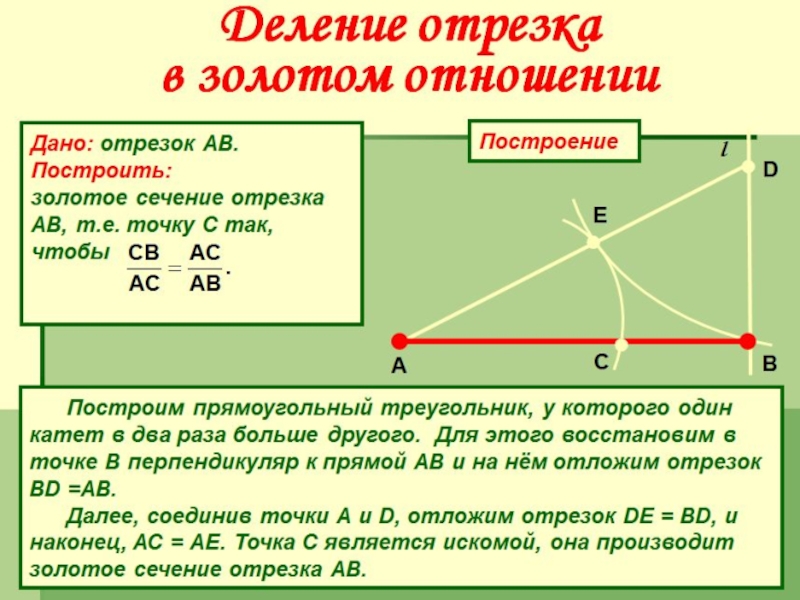
- 6. Разделим отрезок АВ точкой С в таком
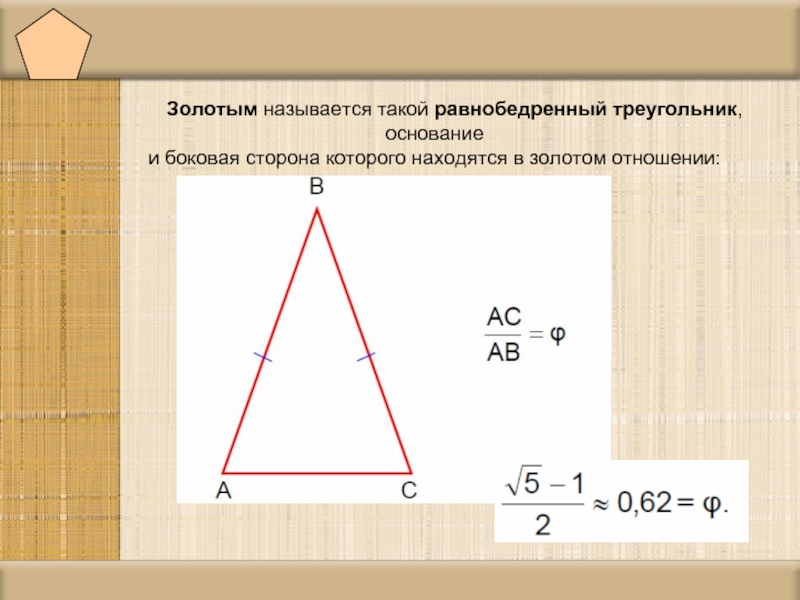
- 8. Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении:
- 9. Окружающие нас предметы дают примеры золотого прямоугольника:
- 10. «Сравнение математических фигур и величин служит
- 11. «Есть в математике нечто вызывающее восторг»
- 12. «Геометрия обладает двумя великими сокровищами - это
- 13. «Не знающий геометрии да не войдёт в
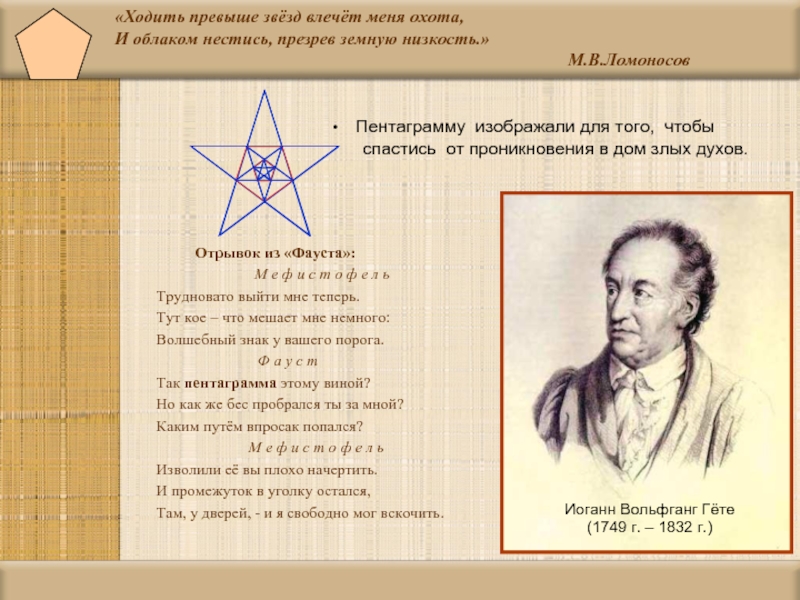
- 14. «Ходить превыше звёзд влечёт меня охота, И
- 15. «Если бы мне пришлось начать
- 16. «Да, путь познания не гладок,
- 17. «Мышление начинается с удивления»
- 18. «Гёте удачно назвал благородный собор «окаменелой
- 19. «…, но, быть может, ещё лучше было
- 20. «Поистине живопись – наука и законная дочь
- 21. Портрет «Мона Лиза» (Джоконда) долгие годы привлекает
- 22. На подготовительном эскизе Рафаэля проведены линии, идущие
- 23. Музыка Скрипка создавалась по чертежу, в основе
- 24. Отношение высот нижней и верхней частей, на
- 25. «Высшее назначение математики…состоит в том, чтобы находить
- 26. «Пристальное и глубокое изучение природы есть источник
- 29. Золотое сечение в природе Все, что приобретало
- 32. Цветки и семена подсолнуха, ромашки, чешуйки в
- 33. Кристаллы пирита имеют форму додекаэдра – поверхности,
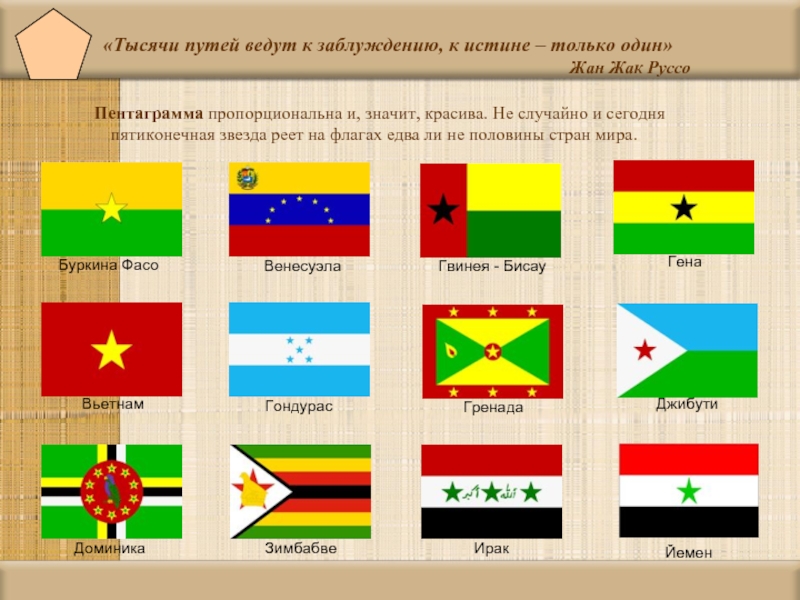
- 34. «Тысячи путей ведут к заблуждению, к истине
- 35. «Мудрее всего – время, ибо оно раскрывает
- 36. «Ни тридцать лет ни тридцать столетий не
- 37. «Кто любит учиться - никогда не проводит
- 38. « В задачах, которые ставит перед нами
- 39. Золотое сечение и мода Присмотритесь к своей
- 40. 1. золотое сечение – это один из
- 41. Список используемой литературы А.В. Волошинов. Пифагор.- М:
Слайд 1ЗОЛОТОЕ СЕЧЕНИЕ
Выполнили: ученики 8 «А» класса
Иванин Андрей и Кокотко Вячеслав
Музыка
Морис Клайн
Слайд 2Цель данной работы:
изучить геометрическое определение "золотого сечения";
изучить алгебраические свойства золотой
узнать о применении золотого сечения в математике ;
изучить применение золотого сечения в жизни человека ;
способствовать познанию законов красоты и гармонии окружающего мира.
Слайд 3Содержание
Понятие золотого сечения
Основатели учения о золотом сечении
Золотое сечение в
Золотое сечение в живописи
Золотое сечение в живых организмах
Пентаграмма
Самый «правильный» многогранник
Золотое сечение вокруг нас
Список используемой литературы
Слайд 6Разделим отрезок АВ точкой С в таком отношении, чтобы большая часть
А С В
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
Алгебраическое построение «золотого сечения» АВ=а сводится к решению уравнения a:x=x:(a-x), где x=b, откуда
x= =0,62a.
Отношение x к а может быть так же выражено дробями 2/3, 3/5, 5/8, 8/13, 13/21,…, где 2, 3, 5, 8, 13, 21,… - числа Фибоначчи.
Слайд 8 Золотым называется такой равнобедренный треугольник, основание
и боковая сторона которого находятся в
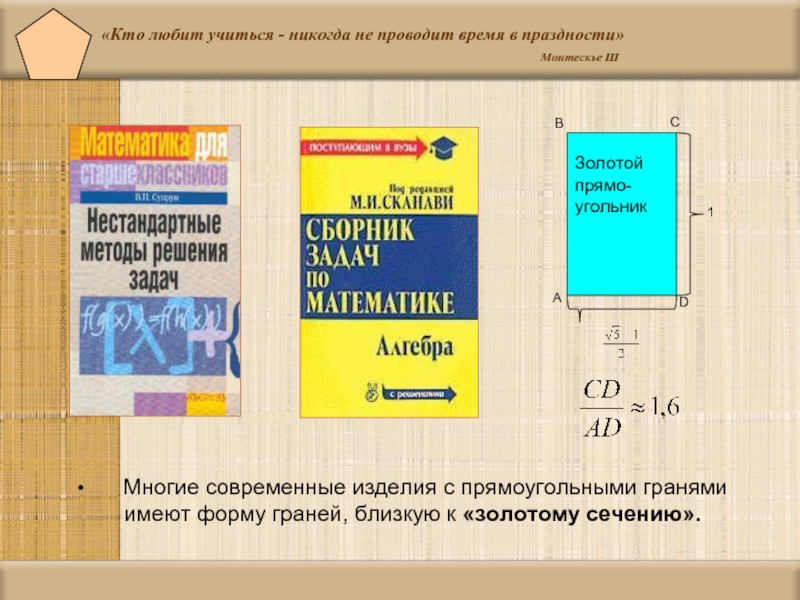
Слайд 9 Окружающие нас предметы дают примеры золотого прямоугольника: обложки многих книг, журналов,
Золотой прямоугольник
Слайд 10«Сравнение математических фигур и величин служит материалом для игр и обучения
Отрезок АВ так относится к его большей части AD, как эта большая часть AD относится к его меньшей части DB.
Иначе говоря, точка D делит отрезок AB в «золотой пропорции».
Первые упоминания о пентаграмме относятся к Древней Греции. В переводе с Греческого пентаграмма означает дословно пять линий (leuta - пять, gramma - черта, линия). В эллинском мире наука и искусство развивались в так называемых философских школах.
Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и золотые отношения будут сохраняться.
Слайд 11«Есть в математике нечто вызывающее восторг»
Есть предположение, что Пифагор понятие золотого сечения позаимствовал у египтян и вавилонян. И, действительно пропорции пирамиды Хеопса, барельефы предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношением золотого сечения при их создании.
Пирамида Хеопса
Слайд 12«Геометрия обладает двумя великими сокровищами - это теорема Пифагора и золотым
Пропорции, т.е. равенства отношений изучались пифагорейцами.
Евдокс развил учение о пропорциях–одно из величайших достижений греческой математики.
Термин «золотое сечение» ввёл Леонардо да Винчи.
Евдокс (408 – ок.355 г.г.до н.э.)
Пифагор (580-500 г.г.до н.э.)
Леонардо да Винчи (1452-1519 г.г.)
Слайд 13«Не знающий геометрии да не войдёт в Академию».
Пентаграмма – тайный знак пифагорейского братства – была выбрана ими в качестве символа жизни и здоровья.
Согласно легенде , один пифагореец заболел на чужбине и не мог перед смертью расплатиться с ухаживающим за ним хозяином дома. Последний нарисовал на стене своего дома звёздчатый пятиугольник. Увидав через несколько лет этот знак, другой странствующий пифагореец осведомился о случившимся у хозяина и щедро его вознаградил.
Слайд 14«Ходить превыше звёзд влечёт меня охота, И облаком нестись, презрев земную низкость.»
Отрывок из «Фауста»:
М е ф и с т о ф е л ь
Трудновато выйти мне теперь.
Тут кое – что мешает мне немного:
Волшебный знак у вашего порога.
Ф а у с т
Так пентаграмма этому виной?
Но как же бес пробрался ты за мной?
Каким путём впросак попался?
М е ф и с т о ф е л ь
Изволили её вы плохо начертить.
И промежуток в уголку остался,
Там, у дверей, - и я свободно мог вскочить.
Пентаграмму изображали для того, чтобы
спастись от проникновения в дом злых духов.
Слайд 15 «Если бы мне пришлось начать вновь своё обучение то
По Платону: пять правильных многогранников – пять стихий. Додекаэдр олицетворяет вселенную.
Платон считал додекаэдр самым «правильным» из всех правильных многогранников, т. к. его грани – правильные пятиугольники – сотканы из золотых пропорций.
Слайд 16«Да, путь познания не гладок, Но знаем мы со школьных
Бог – отец «оберегает» вселенную, имеющую форму додекаэдра.
12 граней додекаэдра и 12 апостолов Христа не просто совпадение - в картине САЛЬВАДОРА ДАЛИ «Тайная вечеря» заключён глубокий религиозный смысл.
Сальвадор Дали
Слайд 17«Мышление начинается с удивления»
Леонардо да Винчи любил мастерить каркасы правильных тел и преподносить их в дар знатным особам, возможно пытаясь таким образом приобщить сильных мира сего к философским размышлениям о красоте вечных истин.
Рисунки Леонардо да Винчи
из книги Луки Пачоли «Божественная пропорция»
Слайд 18 «Гёте удачно назвал благородный собор «окаменелой музыкой», …»
Церковь Покрова Богородицы на Нерли 1165 год
«Простая» красота пропорций золотого сечения.
Слайд 19«…, но, быть может, ещё лучше было бы назвать такой собор
Пропорции Покровского Собора на Красной площади в Москве определяются восемью членами ряда золотого сечения:
Многие члены ряда золотого сечения повторяются в затейливых элементах храма многократно:
Слайд 20«Поистине живопись – наука и законная дочь природы…»
Леонардо да Винчи
Пропорции Венеры выполнены в золотом сечении.
Слайд 21Портрет «Мона Лиза» (Джоконда) долгие годы привлекает внимание исследователей, которые обнаружили,
Слайд 22На подготовительном эскизе Рафаэля проведены линии, идущие от смыслового центра композиции
Слайд 23Музыка
Скрипка создавалась по чертежу, в основе которого лежал принцип золотого сечения.
Параметры хранящейся в Госколлекции скрипки Страдивари работы 17 века.
длина корпуса - 359 мм,
ширина верхней
окружности – 169 мм
нижней – 210 мм;
середины – 115 мм.
Слайд 24Отношение высот нижней и верхней частей, на которые статую делит пупок,
Апллон Бельведерский
Но не только создатель Аполлона, но и скульптор Фидий часто использовал золотую пропорцию в своих произведениях. Самыми
знаменитыми из них были статуя Зевса Олимпийского, которая считалась одним из семи чудес света, и статуя Афины Парфенос.
Фидий руководил строительством храма Парфенон в Афинах.
Слайд 25«Высшее назначение математики…состоит в том, чтобы находить скрытый порядок в хаосе,
«Человеку, сведущему в геометрии и работающему с нею, становятся доступны… все те высшие наслаждения, которые называются наслаждениями математического порядка… Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Стоит поразмыслить о прошлом, вспомнить то, что было ранее, и мы будем ошеломлены, видя, что окружающий нас мир – это мир геометрии, чистой, истинной, безупречной в наших глазах. Всё вокруг – геометрия».
Ле Корбюзье
Пропорции идеальной фигуры человека, по Корбюзье, должны подчиняться золотому сечению.
Модулор Ле Корбюзье
Слайд 26«Пристальное и глубокое изучение природы есть источник
пропорции, близкие к золотому сечению.
Слайд 29Золотое сечение в природе
Все, что приобретало какую-то форму, образовывалось, росло, стремилось
Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.
Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно.
Слайд 32Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках
Слайд 33Кристаллы пирита имеют форму додекаэдра – поверхности, составленной из 12 правильных
Как показывают раскопки в Италии, пирит был любимой игрушкой этрусских детей во времена Пифагора.
Кристаллы пирита
/
Рисунок кристалла пирита
Слайд 34«Тысячи путей ведут к заблуждению, к истине – только один»
Пентаграмма пропорциональна и, значит, красива. Не случайно и сегодня пятиконечная звезда реет на флагах едва ли не половины стран мира.
Слайд 35«Мудрее всего – время, ибо оно раскрывает всё»
Столь необычайно пропорциональное строение пентаграммы, красота
её внутреннего математического содержания
являются основой её внешней красоты.
Слайд 36«Ни тридцать лет ни тридцать столетий не оказывают
Раифский мужской монастырь – единственный в Татарии сохранившийся монастырский комплекс, построенный в XVII веке. Комплекс имеет форму пятиугольника.
Пентагон в США . Комплекс имеет форму правильного пятиугольника, сотканного из золотых пропорций.
Слайд 37«Кто любит учиться - никогда не проводит время в праздности»
Многие современные изделия с прямоугольными гранями
имеют форму граней, близкую к «золотому сечению».
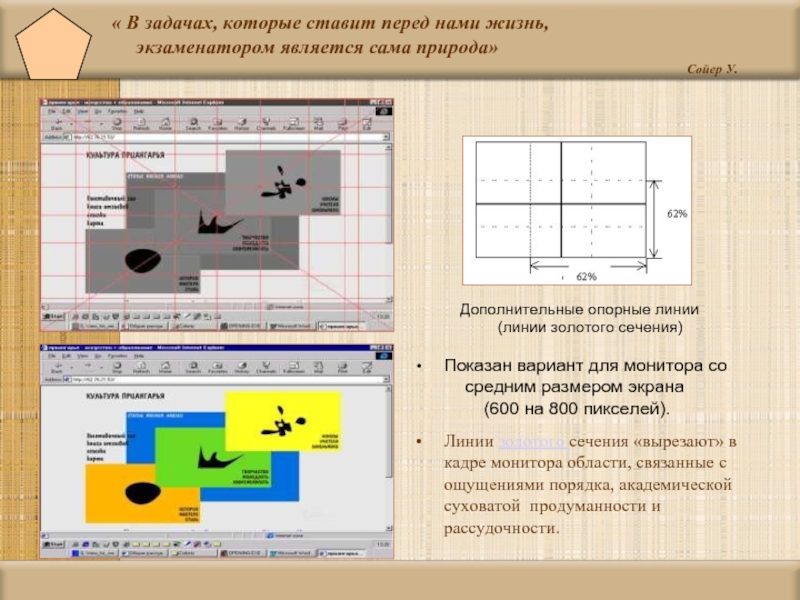
Слайд 38« В задачах, которые ставит перед нами жизнь, экзаменатором
Линии золотого сечения «вырезают» в кадре монитора области, связанные с ощущениями порядка, академической суховатой продуманности и рассудочности.
Дополнительные опорные линии
(линии золотого сечения)
Показан вариант для монитора со
средним размером экрана
(600 на 800 пикселей).
Слайд 39Золотое сечение и мода
Присмотритесь к своей одежде и попробуйте комбинировать вещи
Слайд 401. золотое сечение – это один из основных основополагающих принципов природы;
2.
3. золотое сечение в природе, искусстве, архитектуре является непременным условием правильного и красивого изображения предмета, впоследствии украшающего нашу жизнь.
Работая над проектом, мы пришли к выводу, что красота таинственна, разнообразна и окружает нас повсюду, но вся она поддается одним и тем же законам, знание и применение которых делает нас и жизнь прекраснее.
Выводы:
Слайд 41Список используемой литературы
А.В. Волошинов. Пифагор.- М: «Просвещение» 1993 г.
Г.И. Глейзер. История
Лиман М.М. Школьникам о математике и математиках. М: «Просвещение» 1981 г.
www photoline.ru/tcomp 1.htm.
http//www.nips.riss-telecom.ru/poly/