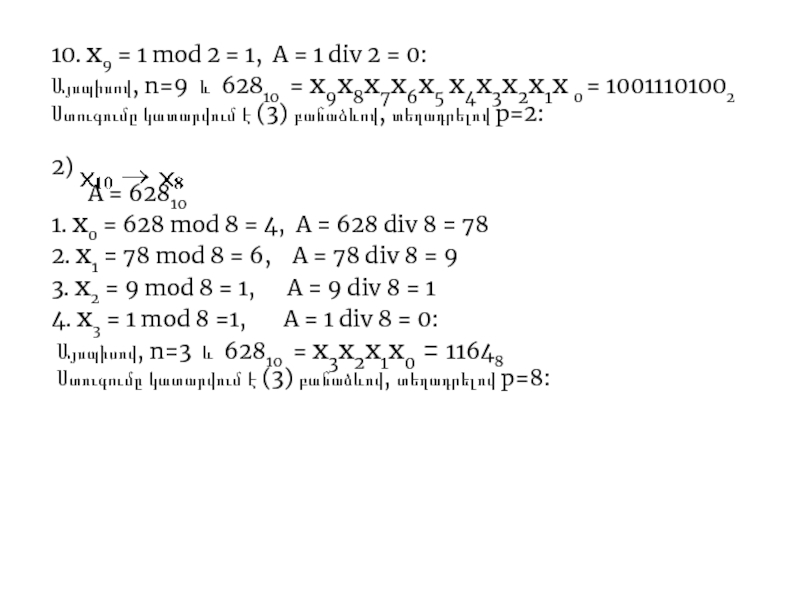- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ինֆորմատիկա презентация
Содержание
- 1. Ինֆորմատիկա
- 2. ՀԱՄԱԿԱՐԳՉԻ ՏՐԱՄԱԲԱՆԱԿԱՆ ՍԽԵՄԱՆ Այս նկարում հանակարգիչը ներկայացված
- 3. ՀԻՇՈՂ ՍԱՐՔԵՐԻ ՏԵՍԱԿՆԵՐԸ և ԿԱՌՈՒՑՎԱԾՔԸ Հիշող
- 4. ԹՎԱՅԻՆ ՀԱՇՎԱՐԿԱՅԻՆ ՀԱՄԱԿԱՐԳԵՐ Դիցուք, p-ն համակարգի հիմքն
- 5. Օրինակներ. 73510 = 7*102 + 3*101 +
- 6. Թվերի ներկայացումը հաշվարկային համակարգերում ԱՄԲՈՂՋ ԹՎԵՐ Դիցուք,
- 7. Այսպես շարունակելով կհասնենք (n+1) քայլին, երբ A
- 8. 10. x9 = 1 mod 2 =
- 9. 3) A =
- 10. (p=2) 1101101 (109) (p=8)
- 11. (3) Բանաձևը զննելիս կարելի է եզրակացնել, որ
- 12. ԿՈՏՈՐԱԿԱՅԻՆ ԹՎԵՐ Դիցուք, տրված է B տասական
- 13. Օրինակներ. 1)
- 14. Սահմանափակվելով 6 կարգ ճշտությամբ, ստանում ենք. n=6
- 15. ԹՎԻ ՆԵՐԿԱՅԱՑՄԱՆ ՎԵՐԱԾՈՒՄԸ ՄԵԿ ՀԱՇՎԱՐԿԱՅԻՆ ՀԱՄԱԿԱՐԳԻՑ ՄՅՈՒՍԸ
- 16. 2) P=8 հիմքով համակարգում տրված է A8
- 17. Բերված դատողությունների հիման վրա ձևափոխված (4) գումարը
- 18. P=2 հիմքով համակարգում տրված A2 = 11010111011
Слайд 1ԻՆՖՈՐՄԱՏԻԿԱ
Տեսական դասընթացներ` ............. 32 ժամ
Գործնական պարապմունքներ` 16 ժամ
Լաբորատոր պարապմունքներ` 16
Ուսումնական պրակտիկա` ......... 10 ժամ
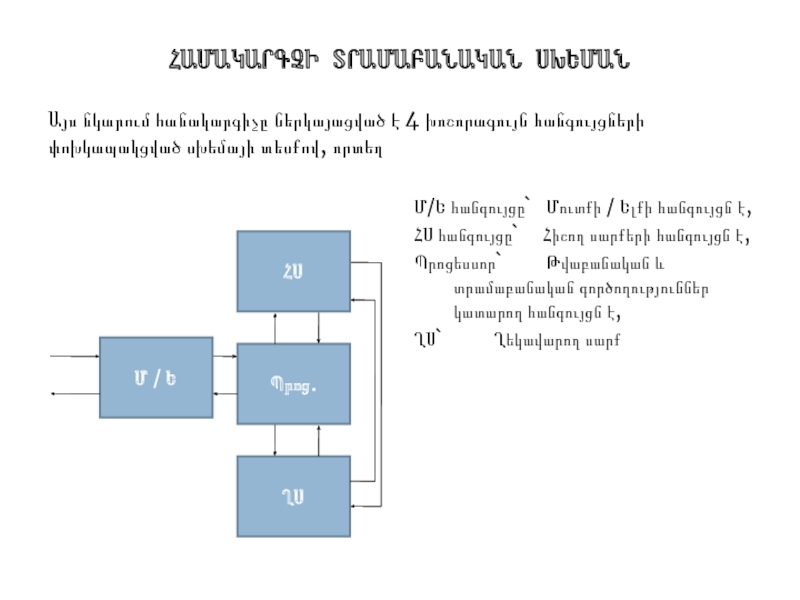
Слайд 2ՀԱՄԱԿԱՐԳՉԻ ՏՐԱՄԱԲԱՆԱԿԱՆ ՍԽԵՄԱՆ
Այս նկարում հանակարգիչը ներկայացված է 4 խոշորագույն հանգույցների փոխկապակցված
Մ/Ե հանգույցը` Մուտքի / Ելքի հանգույցն է,
ՀՍ հանգույցը` Հիշող սարքերի հանգույցն է,
Պրոցեսսոր` Թվաբանական և տրամաբանական գործողություններ
կատարող հանգույցն է,
ՂՍ` Ղեկավարող սարք
Պրոց.
ՂՍ
ՀՍ
Մ / Ե
Слайд 3ՀԻՇՈՂ ՍԱՐՔԵՐԻ ՏԵՍԱԿՆԵՐԸ և ԿԱՌՈՒՑՎԱԾՔԸ
Հիշող սարքերը լինում են.
1. ըստ զբաղեցրած
ներքին (օպերատիվ և հաստատուն),
արտաքին,
2. ըստ օգտագործման եղանակի
ուղիղ դիմումով,
հաջորդական դիմումով:
Անկախ հիշող սարքի տեսակից նրանք բոլորն ունեն բայթային կառուցվածք.
7 6 5 4 3 2 1 0 բիտ
Ամենամեծ թիվը, որը կարող է գրանցվել մեկ բայթում, դա 8 հատ ‘1’ թվանիշից կազմված`11111111 թիվն է, որը համարժեք է 255 արժեք ունեցող թվին: Այսինքն,
25510 = 111111112
Ինչպես 255=2*102+5*101+5*100 , այնպես էլ
11111111=1*27 +1*26 +1*25 + 1*24 +1*23 +
+1*22 +1*21 +1*20
= 255
Բայթի պարունակությունը կարող է լինել ոչ միայն թիվ, այլ նաև որև է նշանի գաղտնագիր :
Слайд 4ԹՎԱՅԻՆ ՀԱՇՎԱՐԿԱՅԻՆ ՀԱՄԱԿԱՐԳԵՐ
Դիցուք, p-ն համակարգի հիմքն է:
Հետևաբար, այդ հիմքում թվերը ներկայացնելու
P=10-ի դեպքում T10 = {0,1,2,3,4,5,6,7,8,9},
P=2-ի դեպքում T2 = {0,1},
P=8-ի դեպքում T 8 = {0,1,2,3,4,5,6,7},
P=16-ի դեպքում T 16 = {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F},
որտեղ A-ն փոխարինում է 10 թվանիշին,
B-ն`11 թվ., C-ն` 12 թվ., D-ն` 13 թվ., E-ն` 14 թվ. և F -ն` 15 թվ.:
P հիմքով համակարգի Xp = xnxn-1 … x1x0 ամբողջ թվի արժեքը կարելի է հաշվել հետևյալ հայտնի բանաձևով.
xnpn + xn-1pn-1 + … + x1p1 + x0p0 (1)
Слайд 5Օրինակներ.
73510 = 7*102 + 3*101 + 5*100 ,
1101010112 = 1*28 +
7358 = 7*82 + 3*81 + 5*80 = 477
3BF716 = 3*163 + 11*162 + 15*161 + 7*160 = 15351
P հիմքով համակարգի Yp = 0,x-1x-2 … xn-1xn կոտորակային թվի արժեքը կարելի է հաշվել հետևյալ հայտնի բանաձևով.
x-1p-1 + x-2p-2 + … + x-(n-1)p-(n-1) + x-np-n (2)
Օրինակներ.
0.468 =
0.1101012 =
0.37258 =
Слайд 6Թվերի ներկայացումը հաշվարկային համակարգերում
ԱՄԲՈՂՋ ԹՎԵՐ
Դիցուք, տրված է A տասական ամբողջ թիվը,
Համաձայն (1) – ի կարելի գրել, որ
xnpn + xn-1pn-1 + … + x1p1 + x0 = A (3)
1 քայլ. ա) կամ x0 := A mod p,
բ) կամ A := A div p և
A = xnpn-1 + xn-1pn-2+ … + x2p1 + x1:
2 քայլ. ա) կամ x1 := A mod p,
բ) կամ A := A div p և
A = xnpn-2 + xn-1pn-3+ … + x3p1 + x2:
Слайд 7Այսպես շարունակելով կհասնենք (n+1) քայլին, երբ A = xnp0 և (n+1)
Слайд 810. x9 = 1 mod 2 = 1, A = 1
Слайд 93) A = 1159110 1. x0 = 11591 mod
Слайд 10 (p=2) 1101101 (109) (p=8) 746
1101101 3630
1101101 -----------------
------------------------ 40214 (16524)
10010101111 (1199)
100101011112 = 210+ 27+ 25+ 23+ 22+ 21+ 20 = 1024+128+32+8+4+2+1= 1199
402148 = 4*84 + 2*82 + 1*81 + 4*80 = 16384 + 128 + 8 + 4 = 16524
Слайд 11(3) Բանաձևը զննելիս կարելի է եզրակացնել, որ երկուական ամբողջ թվի արժեքը
A = xn2n + xn-12n-1 + … + x121 + x0 : (4)
Օրինակ, A=47510 թիվը կարելի է ներկայացնել հետևյալ գումարի տեսքով.
475 = 256 + 128 + 64 + 16 + 8 + 2 + 1 կամ
475 = 28 + 27 + 26 + 24 + 23 + 21 + 20 :
Յուրաքանչյուր գումարելին փոխարինվում է ‘1’ թվանշանով, իսկ գումարելիների շարքում 2-ի բացակայող աստիճանների փոխարեն դրվում են ‘0’ թվանշաններ: Այսպիսով, ստանում ենք, որ
A = 47510 = 1110110112
Слайд 12ԿՈՏՈՐԱԿԱՅԻՆ ԹՎԵՐ
Դիցուք, տրված է B տասական կոտորակային թիվը, որը p հիմքով
x-1p-1 + x-2p-2 + … + x-(n-1)p-(n-1) + x-np-n = B
1 քայլ. ա) կամ x-1=trunc(B*p) բ) կամ B:=frac(B*p) և
B = x-2p-1 + x-3p-2 + … + x-(n-1)p-(n-2) + x-np- (n-1)
2 քայլ. ա) կամ x-1=trunc(B*p) բ) կամ B:=frac(B*p) և
B = x-3p-1 + x-4p-2 + … + x-(n-1)p-(n-3) + x-np- (n-2)
Այս գործընթացը կավարտվի երբ B-ի արժեքը կհավասարվի ‘0’-ին:
Սակայն ավելի հաճախ խոսում են` որոշակի ճշտությամբ կոտորակի ներկայացման մասին:
Слайд 13Օրինակներ.
1)
ա) B = 0,687510
1. x-1 =
2. x-2 = trunc(0.375*2) = 0, B := 0.75
3. x-3 = trunc(0.75*2) = 1, B := 0.5
4. x-4 = trunc(0.5*2) = 1, B := 0.0
Այսպիսով, n=4 և 0,687510 = x-1p-1 + x-2p-2 + x-3p-3 + x-4p-4 = 0.10112
բ) B = 0,678510
1. x-1 = trunc(0.6785*2) = 1, B := 0.357
2. x-2 = trunc(0.357*2) = 0, B := 0.714
3. x-3 = trunc(0.714*2) = 1, B := 0.428
4. x-4 = trunc(0.428*2) = 0, B := 0.856
5. x-5 = trunc(0.856*2) = 1, B := 0.712
6. x-6 = trunc(0.712*2) = 1, B := 0.424 և այլն:
Слайд 14Սահմանափակվելով 6 կարգ ճշտությամբ, ստանում ենք. n=6 և
0.678510 ≅ 0.1010112
2)
B
1. x-1 = trunc(0.6785*8) = 5, B := 0.428
2. x-2 = trunc(0.428*8) = 3, B := 0.424
3. x-3 = trunc(0.424*8) = 3, B := 0.392
4. x-4 = trunc(0.392*8) = 3, B := 0.136
5. x-5 = trunc(0.136*8) = 1, B := 0.088
6. x-6 = trunc(0.088*8) = 0, B := 0.684
7. x-7 = trunc(0.684*8) = 5, B := 0.472 և այլն:
Սահմանափակվելով 7 կարգ ճշտությամբ, ստանում ենք. n=7 և
0.678510 ≅ 0.53331058
Слайд 15ԹՎԻ ՆԵՐԿԱՅԱՑՄԱՆ ՎԵՐԱԾՈՒՄԸ ՄԵԿ ՀԱՇՎԱՐԿԱՅԻՆ ՀԱՄԱԿԱՐԳԻՑ ՄՅՈՒՍԸ
Ընդհանուր դեպքում թվի ներկայացման վերածումը
P=2 հիմքով համակարգում տրված է A2 = 11010111011 թիվը: Պահանջվում է տրված թիվը ներկայացնել Q=8 հիմքով հաշվարկային համակարգում:
1. Կատարում ենք վերածումը, գումարելով 2-ի համապատասխան աստիճանները.
A10 = 210+ 29+ 27+ 25+ 24+ 23+ 21+ 20 = 1024+512+128+32+16+8+2+1= 1723
2. Կատարում ենք վերածումը, հաջորդաբար բաժանելով A10 թիվը 8-ի վրա, վերցնելով հերթական մնացորդը և փոքրացնելով A10 -ը 8 անգամ. A8 = 32738 :
Слайд 162) P=8 հիմքով համակարգում տրված է A8 = 67543 թիվը:
1. Կատարում ենք վերածումը.
A10 = 6*84 + 7*83 + 5*82 + 4*81 + 3 = 24576 + 3584 + 320 + 32 + 3 = 28803:
2. Կատարում ենք վերածումը, հաջորդաբար բաժանելով A10 թիվը 16-ի վրա, վերցնելով հերթական մնացորդը և փոքրացնելով A10 -ը 16 անգամ. A16 = 708316 :
Սակայն մասնավոր դեպքերում, երբ Q=Pհ կամ P=Qk ամբողջ k և հ աստիճանացույցների համար, հնարավոր է թվերի պատկերների վերածումը իրականացնել առանց միջանկյալ` 10-ական համակարգի: Անդրադառնանք (4) բանաձևին և ձևափոխենք այն.
xn2n +xn-12n-1+ … +(x828 + x727 + x626 )+(x525 + x424 + x323 )+(x222 + x121 + x0) =
= xn 2n +xn-12n-1 + 26(x822 + x721 + x6 )+ 23 (x522 + x421 + x3)+ 20(x222 + x121 + x0):
Տեղադրենք. 20–ի փոխարեն 80, 23–ի փոխարեն 81, 26–ի փոխարեն 82 և այլն: Յուրաքանչյուր զույգ փակագծերի ներսում ներկայացված երեք գումարելիների գերագույն արժեքը չի գերազանցում 7 արժեքը:
Слайд 17Բերված դատողությունների հիման վրա ձևափոխված (4) գումարը կարող ենք ներկայացնել 8-ի
xn2n + xn-12n-1 + … + x222 + x121 + x0 = ym8m + ym-18m-1 + … + y282 + y181 + y0
և թվի պատկերը 2-ական համակարգից 8-ական վերածելու համար նրա թվանշանները բաժանվում են եռյակների` սկսած միավոր թվանշանից ու փոխարինվում համապատասխան 8-ական թվանշանով: Եթե ավագ կարգերում եռյակ չի ձևավորվում, ապա առջևից լրացվում է ‘0’ թվանշաններով:
Այս ամենը հնարավոր դարձավ, քանի որ 8=23 (Q=P3):
Նույն սկզբունքով կարելի է թվի պատկերը 2-ական համակարգից վեր ածել 16-ական համակարգ, քանի որ 16=24 (Q=P4): Այս դեպքում թվի երկուական պատկերը բաժանվում է քառյակների և յուրաքնչյուր քառյակ փոխարինվում է համապատասխան 16-ական թվանշանով:
Օրինակներ.
Слайд 18P=2 հիմքով համակարգում տրված A2 = 11010111011 թիվը 8-ական համակարգ վերածելու
A2 = 011_010_111_011 = 32738
2) P=2 հիմքով համակարգում տրված A2 = 11010111011 թիվը 16-ական համակարգ վերածելու համար այն բաժանում ենք քառյակների, որոնց հետո փոխարինում ենք համարժեք 16-ական թվանշաններով.
A2 = 0110_1011_1011 = 6BB16
Դիտարկված օրինակներում Q>P : Հակառակ դեպքերում, երբ P>Q (P=Qk) կատարում ենք հետևյալը. P հիմքով համակարգում տրված թվի յուրաքանչյուր թվանշան փոխարինում ենք նրա k-կարգանի պատկերով Q համակարգում: Օրինակ,
k=3 դեպքում. 728 = 111_0102 , 36 8 = 011_1102 ,
k=4 դեպքում. CB8116 = 1100_1011_1000_00012 :