- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в техническое зрение презентация
Содержание
- 1. Введение в техническое зрение
- 2. Модель камеры Камера и человеческий глаз
- 3. Проективная геометрия и модели камеры Slides from
- 4. Что нужно, чтобы сделать камеру?
- 5. Какого роста женщина? Который мяч ближе? Как
- 6. Давайте сделаем камеру Идея 1: поместим плёнку
- 7. Идея 2: добавим барьер и отсечем почти
- 8. Figure from Forsyth f f = фокусное
- 9. Известна со времен Древнего Китая и Греции
- 10. Lens Based Camera Obscura, 1568 Камера-обскура: применение (обводка)
- 11. Самая старая сохранившаяся фотография 8 часов, пьютерная
- 12. Первые фотографии: дагерротип, 20 минут 1864 1837
- 13. Figures © Stephen E. Palmer, 2002 Трехмерный
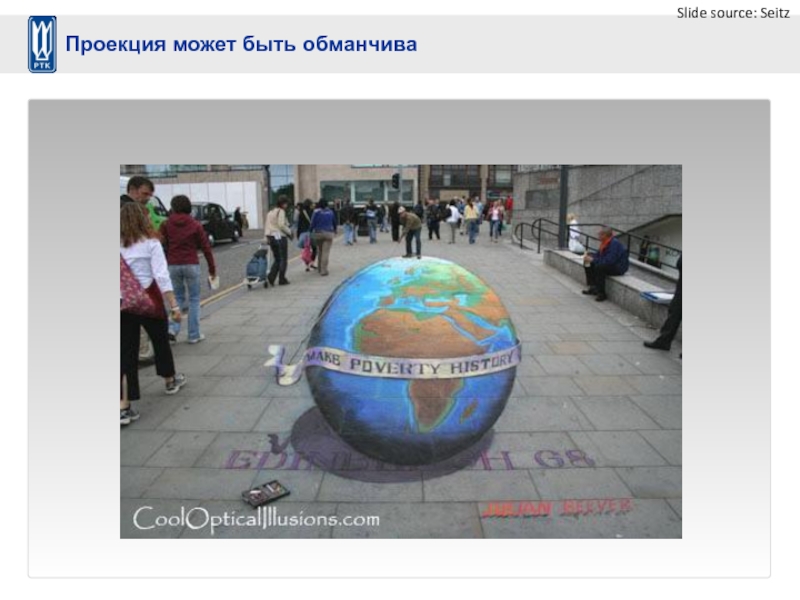
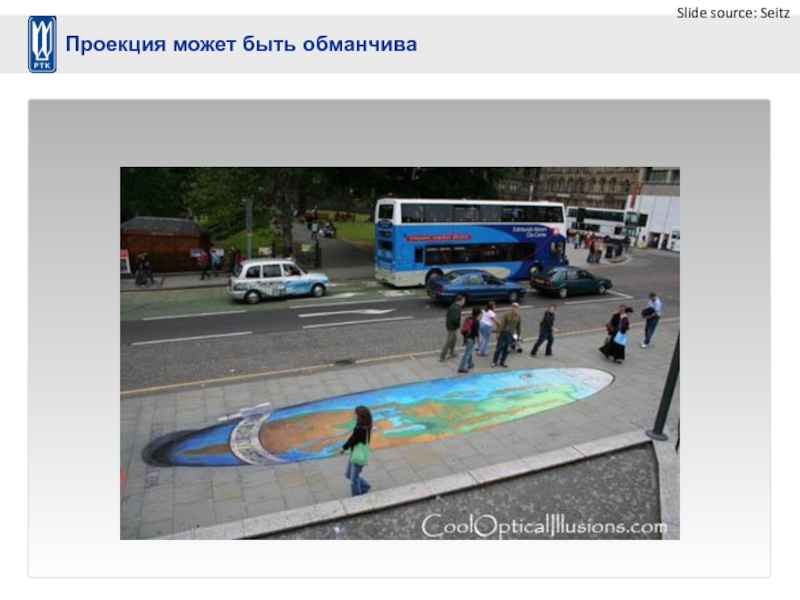
- 14. Slide source: Seitz Проекция может быть обманчива
- 15. Slide source: Seitz Проекция может быть обманчива
- 16. Что теряется? Длина (расстояние) Которые ближе? Кто выше? Проективная геометрия
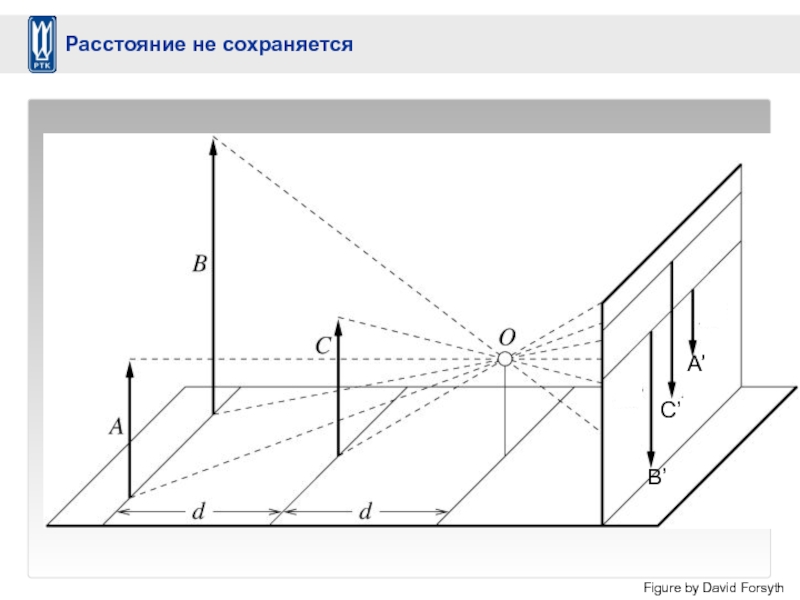
- 17. Figure by David Forsyth B’ C’ A’ Расстояние не сохраняется
- 18. Что теряется? Длина Углы Перпендикулярные? Параллельные? Проективная геометрия
- 19. Что сохраняется? Прямые линии остаются прямыми Проективная геометрия
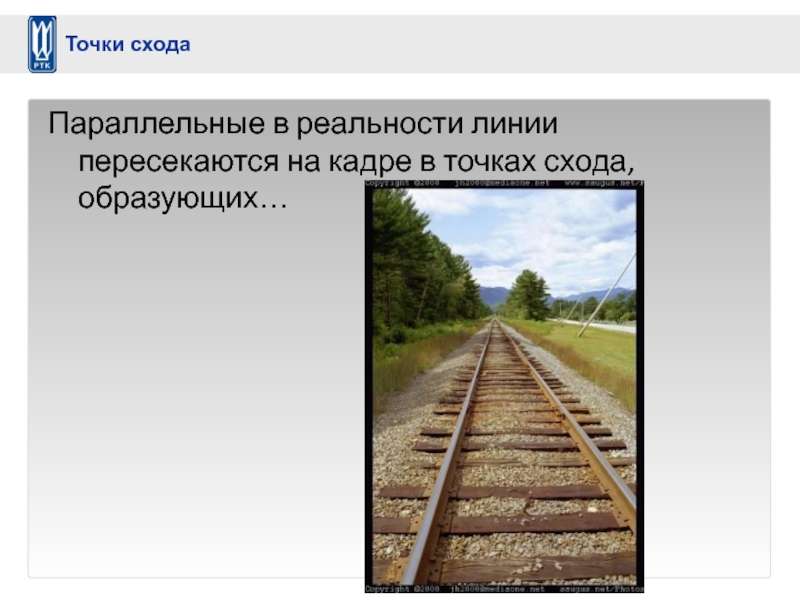
- 20. Параллельные в реальности линии пересекаются на кадре в точках схода, образующих… Точки схода
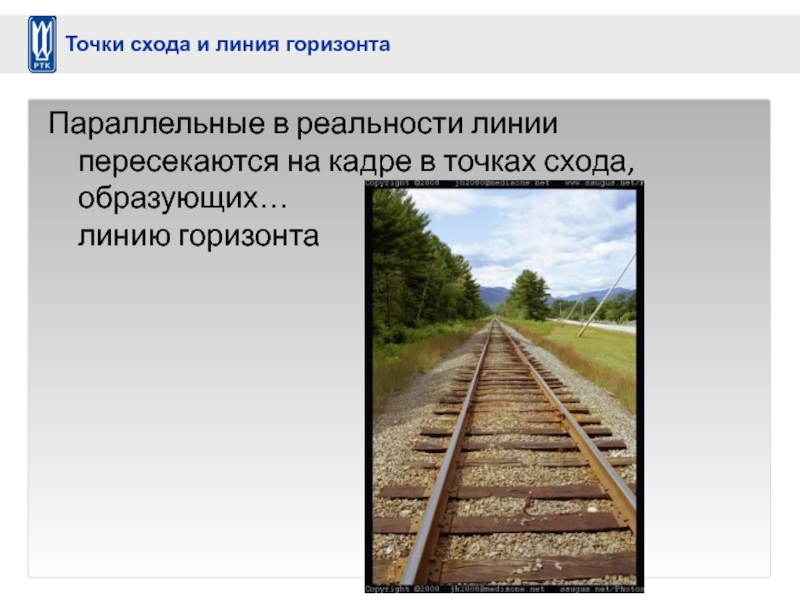
- 21. Параллельные в реальности линии пересекаются на кадре
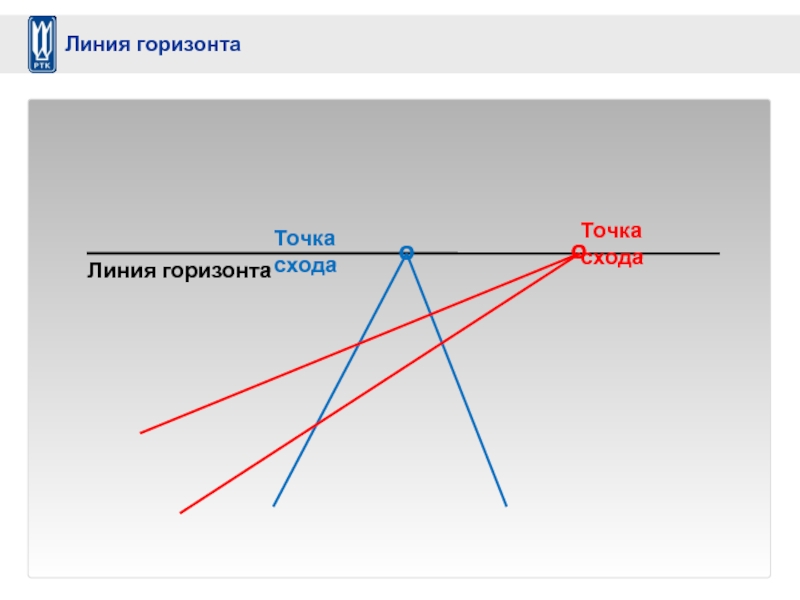
- 22. o Точка схода o Точка схода Линия горизонта Линия горизонта
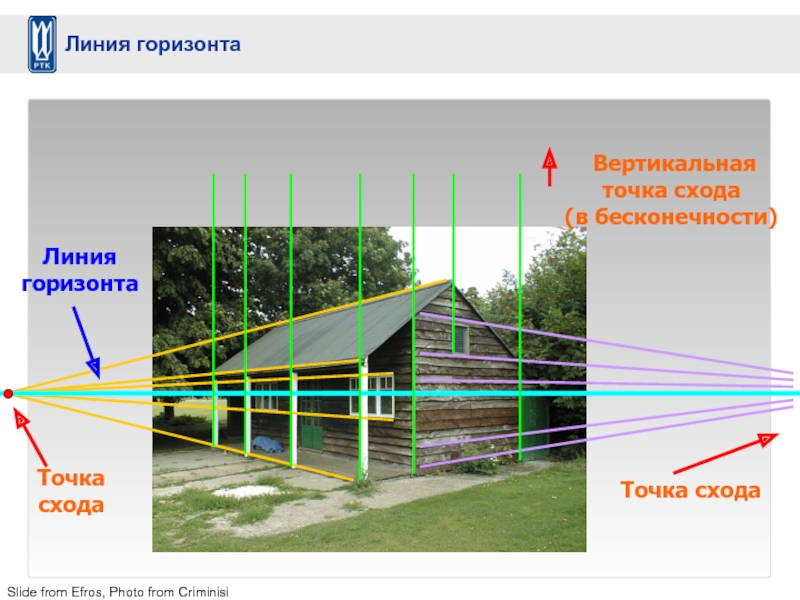
- 23. Slide from Efros, Photo from Criminisi Линия горизонта
- 24. Photo from online Tate collection Линия горизонта
- 25. Линия горизонта
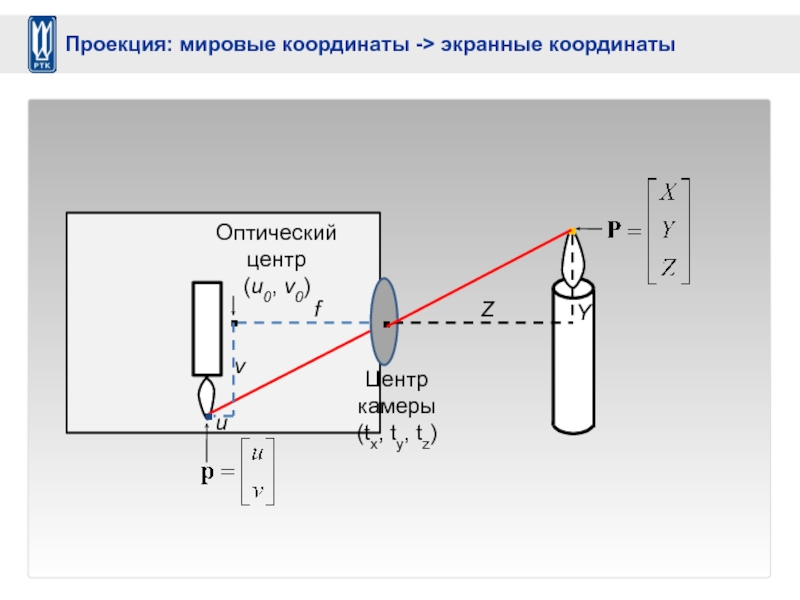
- 26. Проекция: мировые координаты -> экранные координаты
- 27. Преобразование к однородным координатам Однородные
- 28. Инвариантность к масштабу
- 29. Уравнение прямой: ax + by +
- 30. Декартовы: (Inf, Inf) Однородные: (1, 1, 0)
- 31. Slide Credit: Saverese x: Экранные координаты: (u,v,1)
- 32. Соотнесение множества видов Зачем это надо?
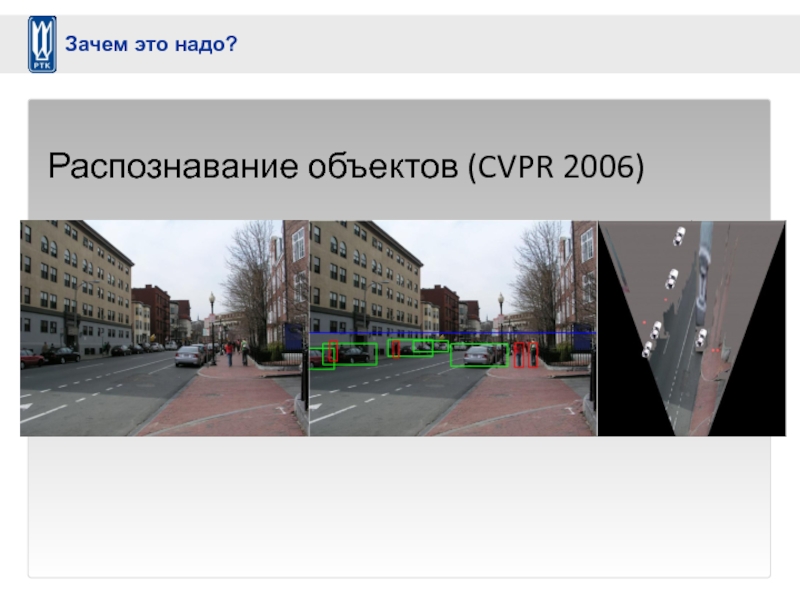
- 33. Распознавание объектов (CVPR 2006) Зачем это надо?
- 34. Дополненная реальность (SIGGRAPH 2007) Оригинал Дополнение Зачем это надо?
- 35. K Slide Credit: Saverese Внутренние допущения
- 36. Внутренние допущения Единичное соотношение
- 37. Внутренние допущения Нет перекоса
- 38. Note: different books use different
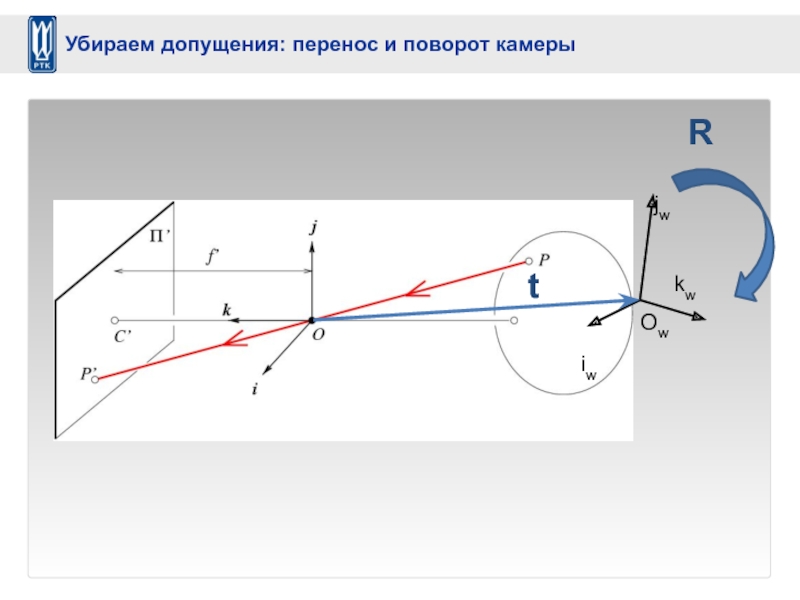
- 39. Ow iw kw jw t R Убираем допущения: перенос и поворот камеры
- 40. Внутренние допущения Внешние допущения Нет поворота Убираем допущения: перенос камеры
- 41. Поворот вокруг координатных осей, против час.стрелки: z Slide Credit: Saverese Трехмерный поворот точек
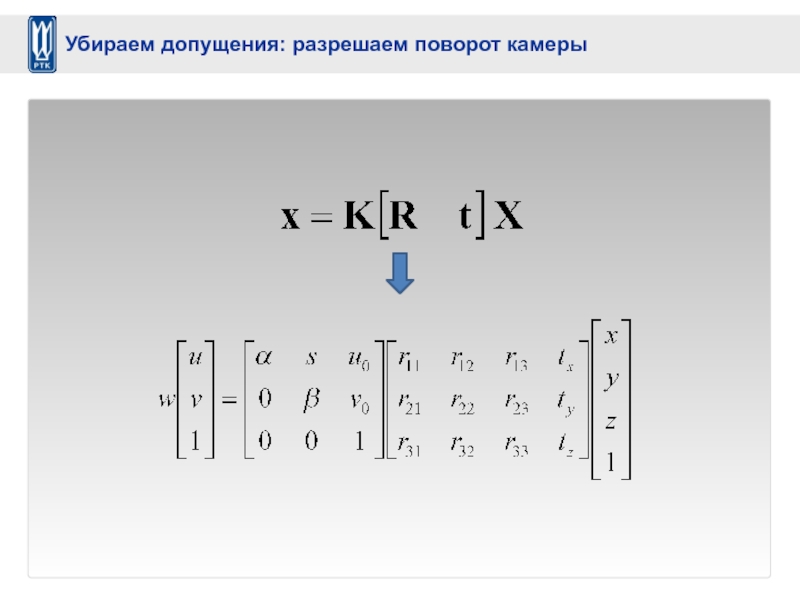
- 42. Убираем допущения: разрешаем поворот камеры
- 43. 5 6 Степени свободы
- 44. Vanishing Point = Projection from Infinity
- 45. Особый случай перспективной проекции
- 46. Особый случай перспективной проекции Размеры объектов малы
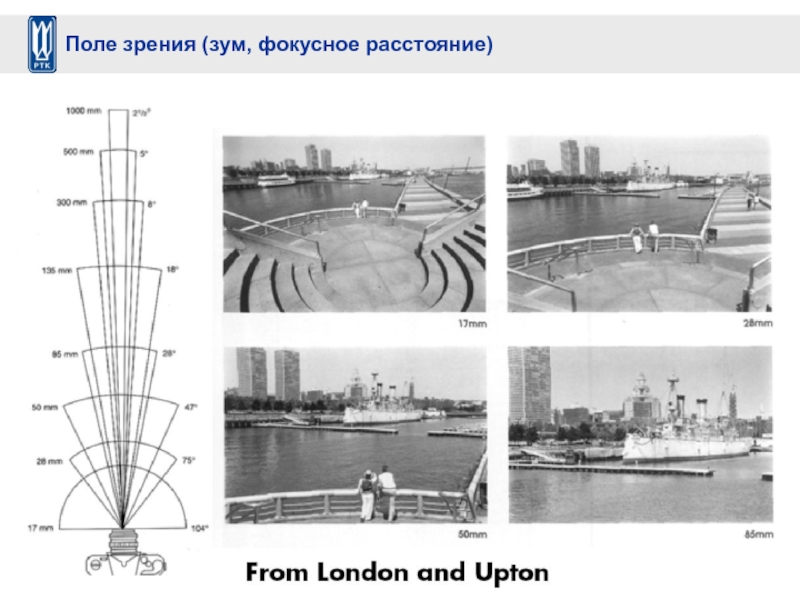
- 47. Поле зрения (зум, фокусное расстояние)
- 48. Suppose we have two 3D cubes on
- 49. Image from Martin Habbecke Коррекция дисторсии (undistort) За пределами камеры-обскуры: радиальная дисторсия
- 50. Точки схода и линия горизонта
- 51. Сделать из «зеркалки» камеру обскура Измерить угол зрения камеры Домашнее задание
- 52. Adding a lens A lens focuses light
- 53. Focal length, aperture, depth of field A
- 54. Depth of field Changing the aperture size
- 55. Shrinking the aperture Why not make the
- 56. Shrinking the aperture Slide by Steve Seitz
- 57. Capturing Light… in man and machine CS
- 58. Image Formation Digital Camera The Eye Film
- 59. A photon’s life choices Absorption Diffusion Reflection
- 60. A photon’s life choices Absorption Diffusion Reflection
- 61. A photon’s life choices Absorption Diffuse Reflection
- 62. A photon’s life choices Absorption Diffusion Specular
- 63. A photon’s life choices Absorption Diffusion Reflection
- 64. A photon’s life choices Absorption Diffusion Reflection
- 65. A photon’s life choices Absorption Diffusion Reflection
- 66. A photon’s life choices Absorption Diffusion Reflection
- 67. A photon’s life choices Absorption Diffusion Reflection
- 68. A photon’s life choices Absorption Diffusion Reflection
- 69. Lambertian Reflectance In computer vision, surfaces are
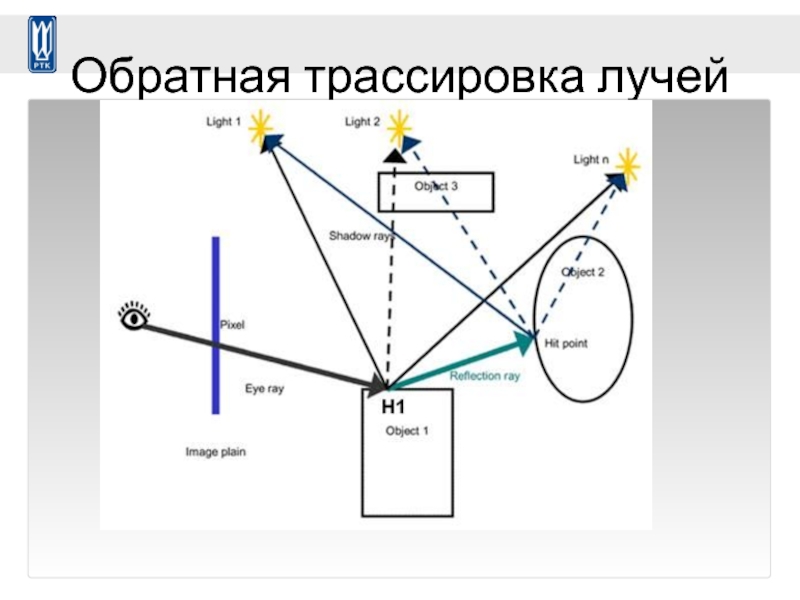
- 70. Обратная трассировка лучей
- 71. Digital camera A digital camera replaces film
- 72. Sensor Array CMOS sensor
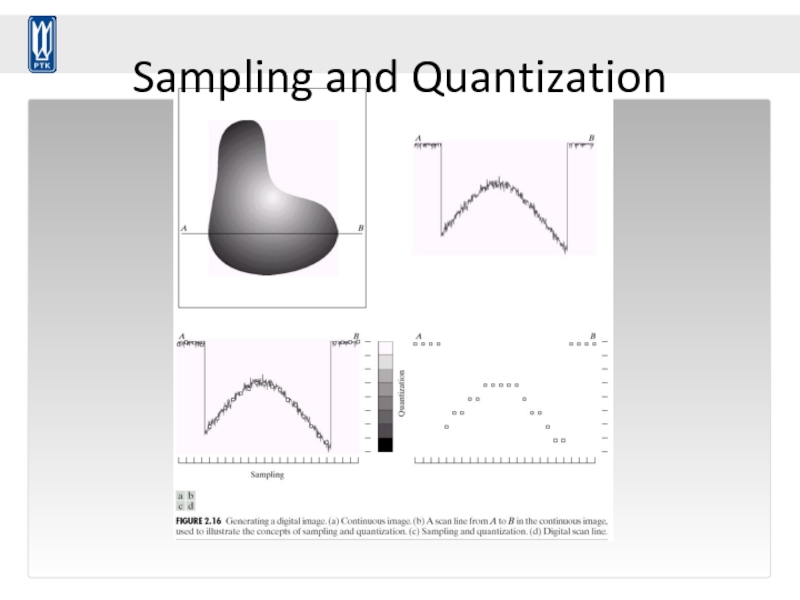
- 73. Sampling and Quantization
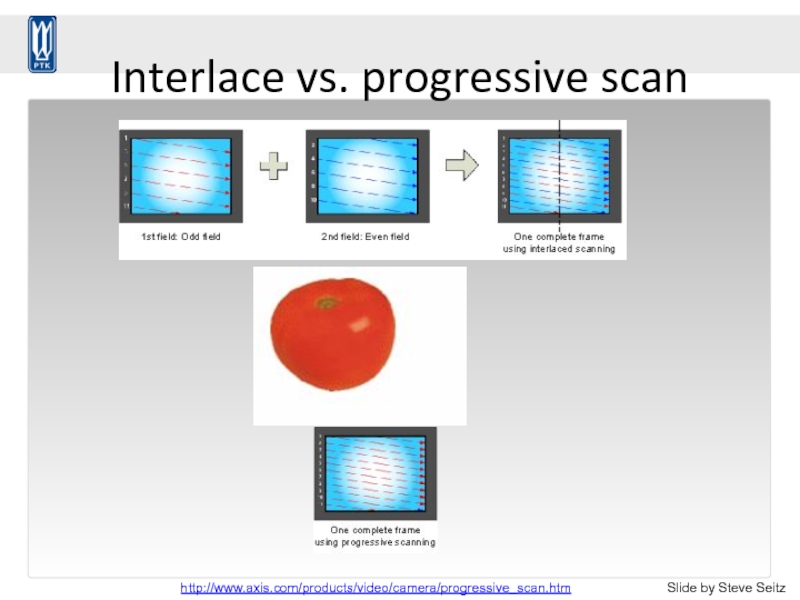
- 74. Interlace vs. progressive scan http://www.axis.com/products/video/camera/progressive_scan.htm Slide by Steve Seitz
- 75. Progressive scan http://www.axis.com/products/video/camera/progressive_scan.htm Slide by Steve Seitz
- 76. Interlace http://www.axis.com/products/video/camera/progressive_scan.htm Slide by Steve Seitz
- 77. Rolling Shutter
- 78. The Eye The human eye is a
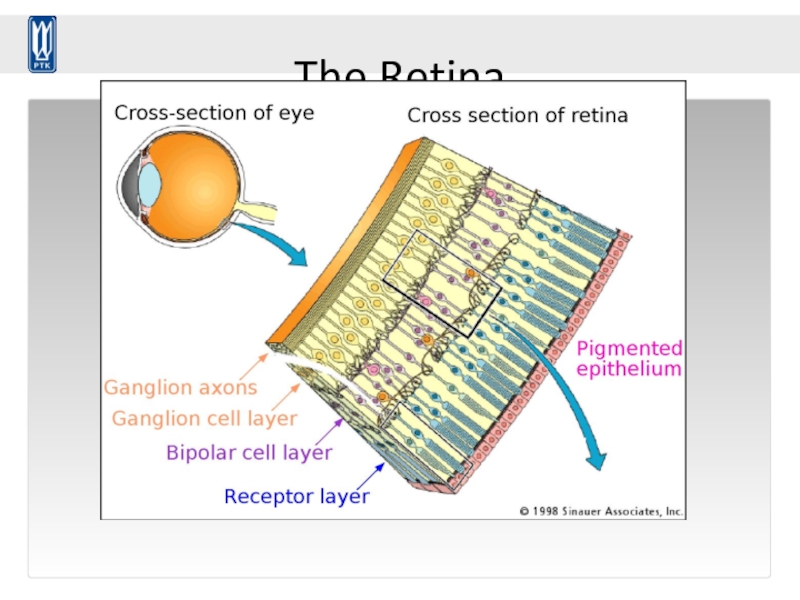
- 79. The Retina
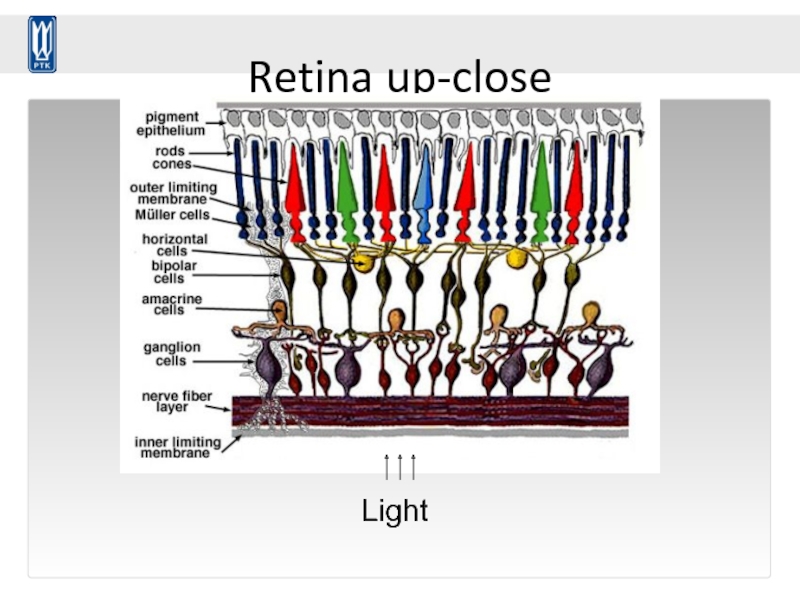
- 80. Retina up-close
- 81. What humans don’t have: tapetum lucidum
- 82. © Stephen E. Palmer, 2002 Cones
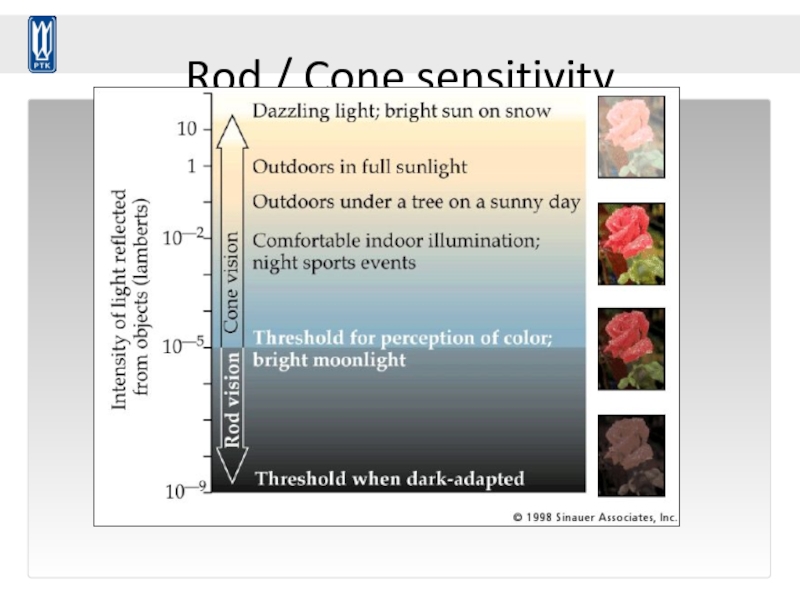
- 83. Rod / Cone sensitivity
- 84. © Stephen E. Palmer, 2002 Distribution of
- 85. Eye Movements Saccades Can be consciously controlled.
- 86. Electromagnetic Spectrum http://www.yorku.ca/eye/photopik.htm Human Luminance Sensitivity Function
- 87. Why do we see
- 88. The Physics of Light Any patch of
- 89. The Physics of Light Some examples of
- 90. The Physics of Light Some examples of
- 91. The Psychophysical Correspondence There is no simple
- 92. The Psychophysical Correspondence Mean Hue © Stephen E. Palmer, 2002
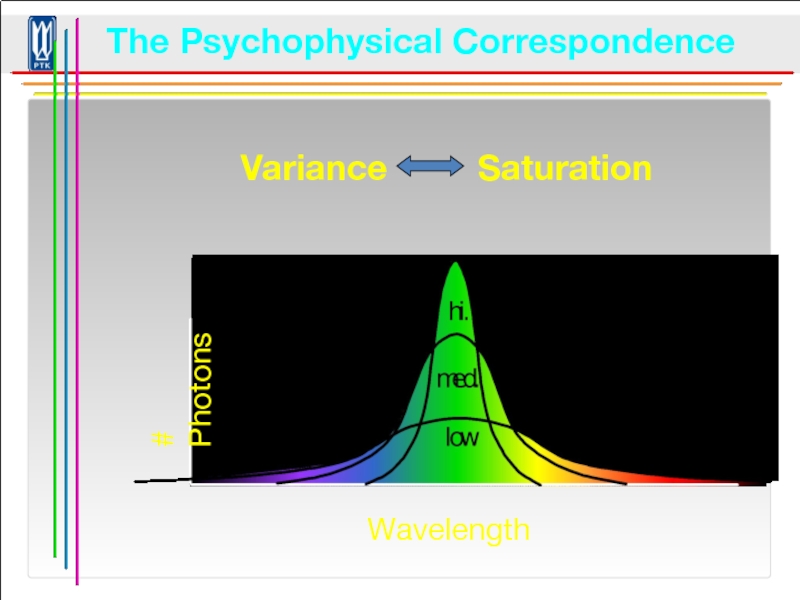
- 93. The Psychophysical Correspondence Variance Saturation © Stephen E. Palmer, 2002
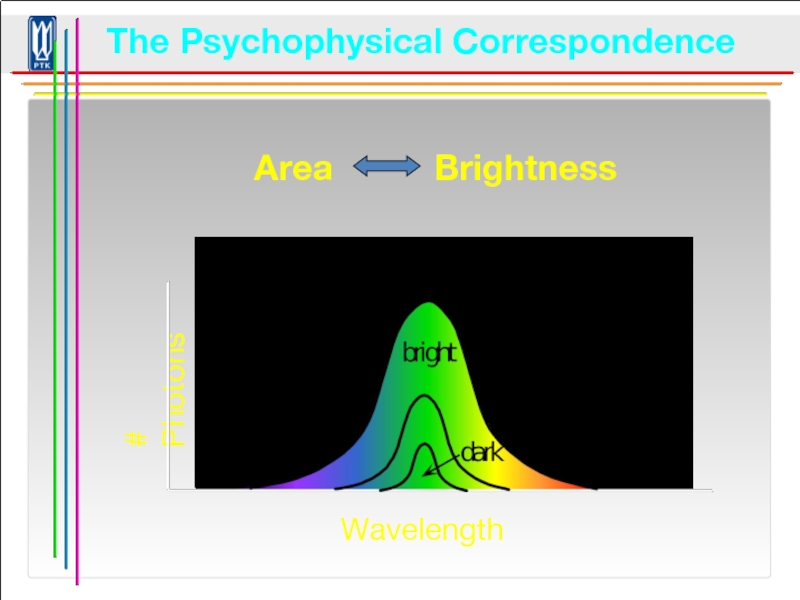
- 94. The Psychophysical Correspondence Area Brightness © Stephen E. Palmer, 2002
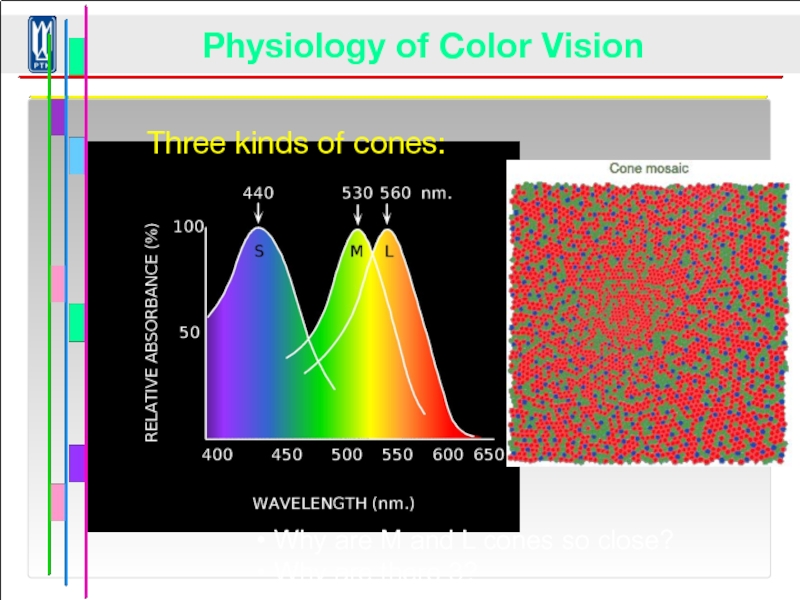
- 95. © Stephen E. Palmer, 2002 Three kinds
- 96. Impossible Colors Can you make the cones
- 97. Tetrachromatism Most birds, and many other animals,
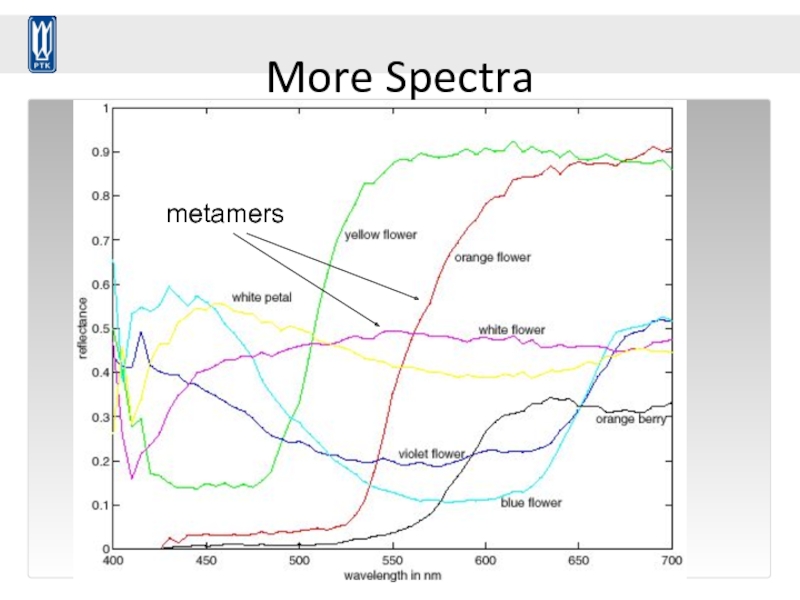
- 98. More Spectra metamers
- 99. Color Sensing in Camera (RGB) 3-chip vs.
- 100. Practical Color Sensing: Bayer Grid Estimate RGB
- 101. Color Image R G B
- 102. Images in Matlab Images represented as a
- 103. Color spaces How can we represent color? http://en.wikipedia.org/wiki/File:RGB_illumination.jpg
- 104. Color spaces: RGB Image from: http://en.wikipedia.org/wiki/File:RGB_color_solid_cube.png Some
- 105. Color spaces: HSV Intuitive color space H (S=1,V=1) S (H=1,V=1) V (H=1,S=0)
- 106. Color spaces: YCbCr Y (Cb=0.5,Cr=0.5) Cb (Y=0.5,Cr=0.5)
- 107. Color spaces: L*a*b* “Perceptually uniform”* color space L (a=0,b=0) a (L=65,b=0) b (L=65,a=0)
- 108. If you had to choose, would you rather go without luminance or chrominance?
- 109. If you had to choose, would you rather go without luminance or chrominance?
- 110. Most information in intensity Only color shown – constant intensity
- 111. Most information in intensity Only intensity shown – constant color
- 112. Most information in intensity Original image
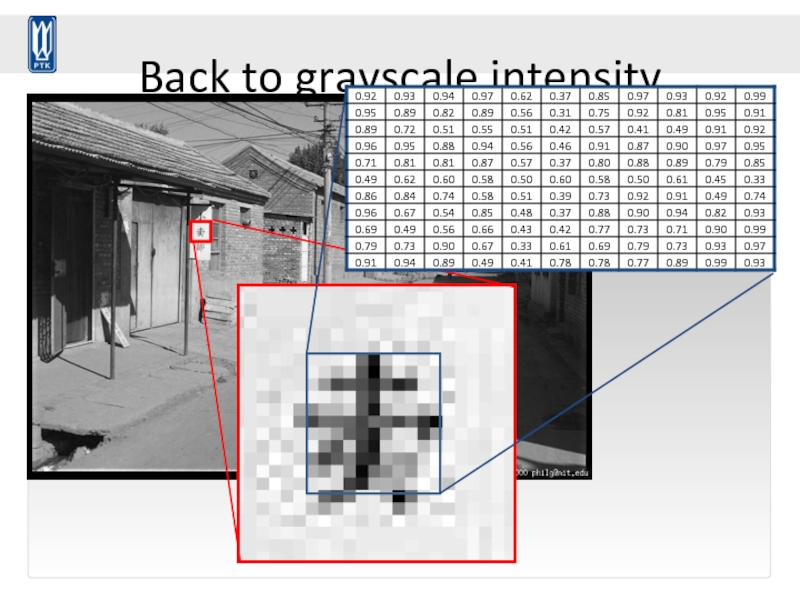
- 113. Back to grayscale intensity
- 114. Восприятие света и цвета Камера и
- 115. Россия, 194064, г. Санкт-Петербург, Тихорецкий пр., 21
Слайд 1
Введение в техническое зрение
Степанов Дмитрий Николаевич
Начальник лаборатории систем технического зрения
dnstepanov@gmail.com
Image by
Слайд 2
Модель камеры
Камера и человеческий глаз
Восприятие света и цвета
Пиксели
Фильтрация изображений
Практическое задание: линейные
Дальше
Слайд 3Проективная геометрия и модели камеры
Slides from Derek Hoiem,
Alexei Efros, Steve
Сегодняшнее занятие
Слайд 5Какого роста женщина?
Который мяч ближе?
Как высоко установлена камера?
Как камера повёрнута?
Каково фокусное
Камера и реальный мир
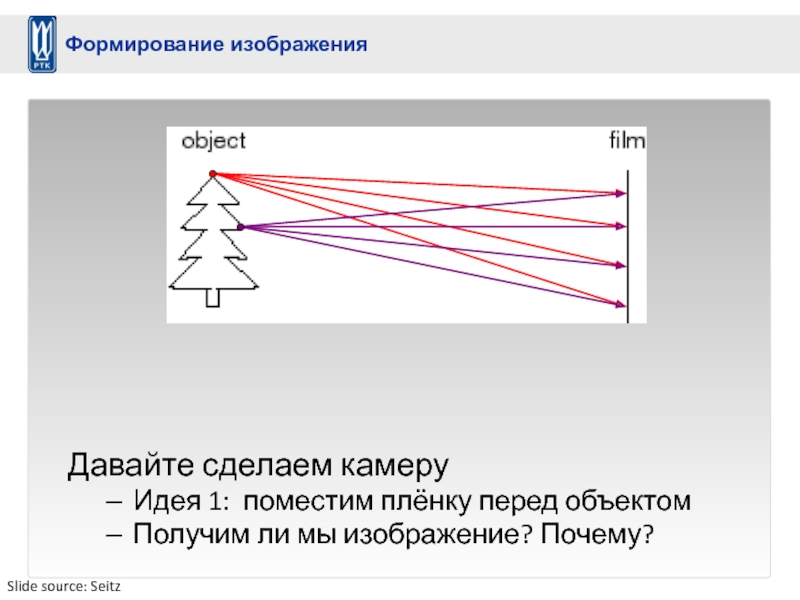
Слайд 6Давайте сделаем камеру
Идея 1: поместим плёнку перед объектом
Получим ли мы изображение?
Slide source: Seitz
Формирование изображения
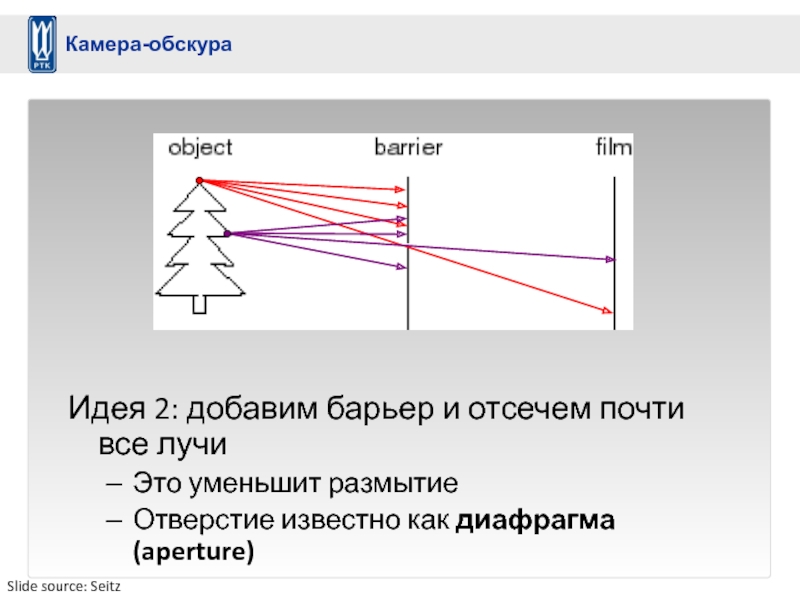
Слайд 7Идея 2: добавим барьер и отсечем почти
все лучи
Это уменьшит размытие
Отверстие известно
Slide source: Seitz
Камера-обскура
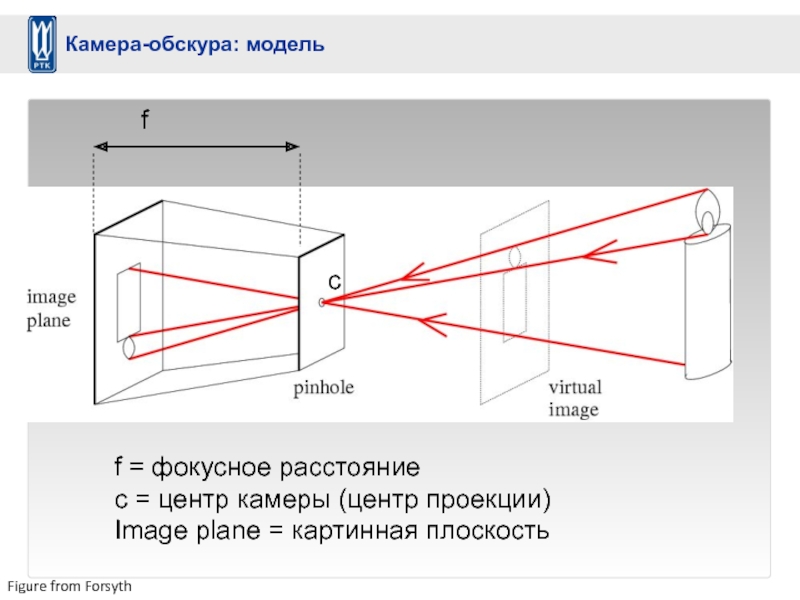
Слайд 8Figure from Forsyth
f
f = фокусное расстояние
c = центр камеры (центр проекции)
Image
c
Камера-обскура: модель
Слайд 9Известна со времен Древнего Китая и Греции
(Mo-Ti, China, 470BC - 390BC)
Иллюстрация
Настоящая камера обскура
в Университете Северной Каролины
Photo by Seth Ilys
Камера-обскура: пре-камера
(лат. camera obscūra — «тёмная комната»)
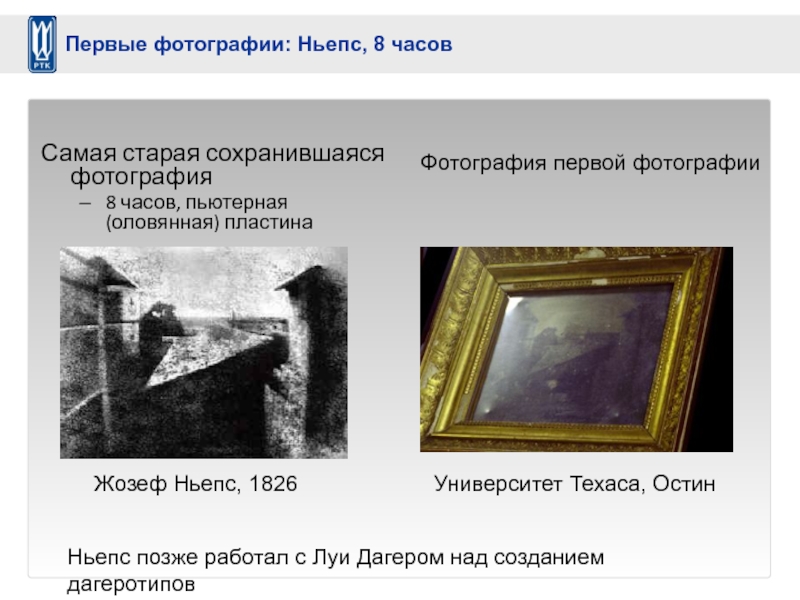
Слайд 11Самая старая сохранившаяся фотография
8 часов, пьютерная (оловянная) пластина
Жозеф Ньепс, 1826
Фотография первой
Университет Техаса, Остин
Ньепс позже работал с Луи Дагером над созданием дагеротипов
Первые фотографии: Ньепс, 8 часов
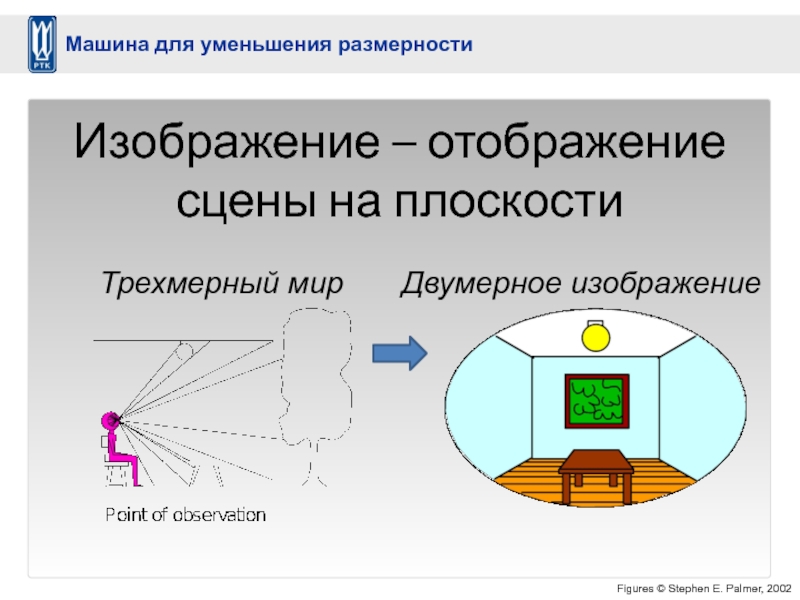
Слайд 13Figures © Stephen E. Palmer, 2002
Трехмерный мир
Двумерное изображение
Изображение – отображение сцены
Машина для уменьшения размерности
Слайд 20Параллельные в реальности линии пересекаются на кадре в точках схода, образующих…
Точки
Слайд 21Параллельные в реальности линии пересекаются на кадре в точках схода, образующих… линию
Точки схода и линия горизонта
Слайд 27
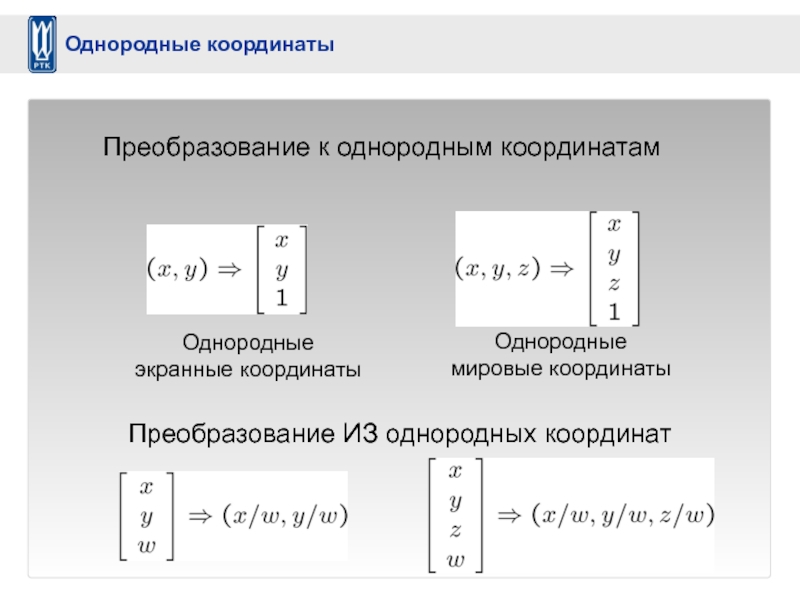
Преобразование к однородным координатам
Однородные
экранные координаты
Однородные
мировые координаты
Преобразование ИЗ однородных координат
Однородные координаты
Слайд 28
Инвариантность к масштабу
Точке в декартовых координатах соответствует луч в однородных
Однородные
координаты
Декартовы
координаты
Однородные координаты
Слайд 29Уравнение прямой:
ax + by + c = 0
Добавить «1» для
Прямая получается как векторное произведение двух точек
Пересечение прямых получается как векторное произведение прямых
Базовая геометрия однородных координат
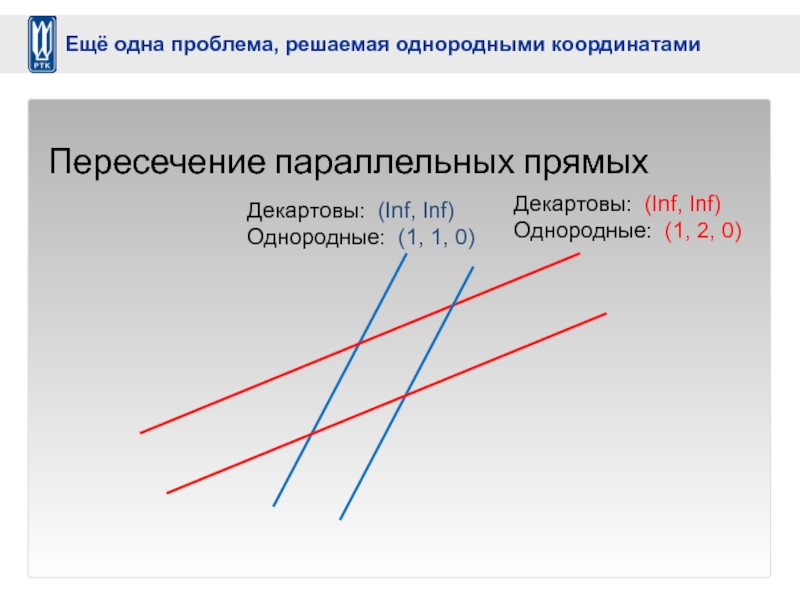
Слайд 30Декартовы: (Inf, Inf)
Однородные: (1, 1, 0)
Пересечение параллельных прямых
Декартовы: (Inf, Inf)
Однородные:
Ещё одна проблема, решаемая однородными координатами
Слайд 31Slide Credit: Saverese
x: Экранные координаты: (u,v,1)
K: Внутренняя матрица (3x3)
R: Вращение (3x3)
t: Перенос (3x1)
X: Мировые координаты: (X,Y,Z,1)
Ow
iw
kw
jw
R,T
Матрица проекции
Слайд 35
K
Slide Credit: Saverese
Внутренние допущения
Единичное соотношение
Оптический центр в (0,0)
Нет
Внешние допущения
Нет поворота
Камера в (0,0,0)
Матрица проекции
Слайд 36
Внутренние допущения
Единичное соотношение
Нет перекоса
Внешние допущения
Нет поворота
Камера в
Убираем допущения: известный оптический центр
Слайд 37
Внутренние допущения
Нет перекоса
Внешние допущения
Нет поворота
Камера в (0,0,0)
Убираем допущения:
Слайд 38
Note: different books use different notation for parameters
Внутренние допущения
Внешние допущения
Нет
Камера в (0,0,0)
Убираем допущения: прямые пиксели
Слайд 41Поворот вокруг координатных осей, против час.стрелки:
z
Slide Credit: Saverese
Трехмерный поворот точек
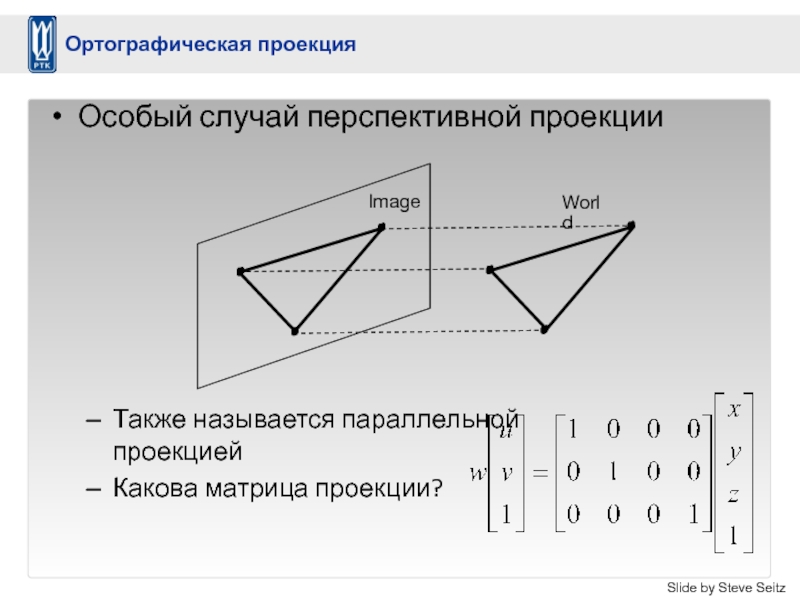
Слайд 45Особый случай перспективной проекции
Также называется параллельной
проекцией
Какова матрица проекции?
Image
World
Slide by Steve Seitz
Ортографическая
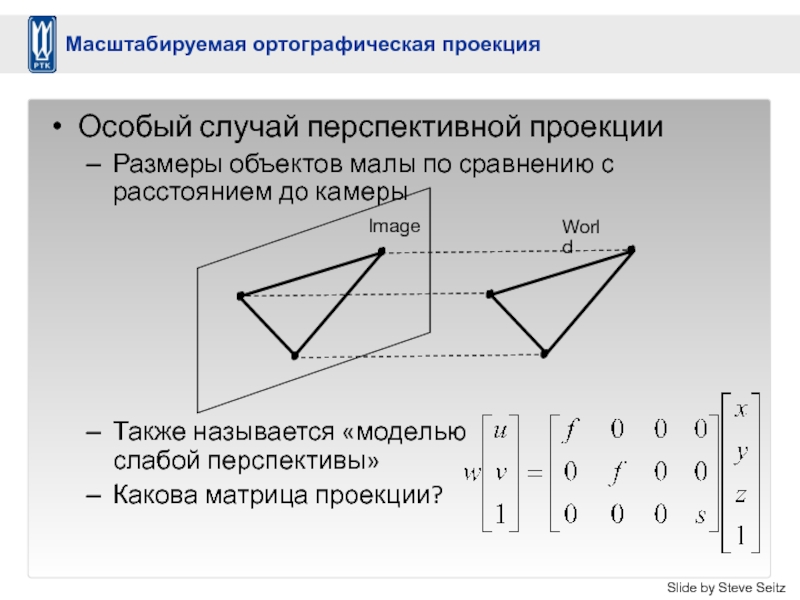
Слайд 46Особый случай перспективной проекции
Размеры объектов малы по сравнению с расстоянием до
Также называется «моделью слабой перспективы»
Какова матрица проекции?
Image
World
Slide by Steve Seitz
Масштабируемая ортографическая проекция
Слайд 48 Suppose we have two 3D cubes on the ground facing the
What would they look like in perspective?
What would they look like in weak perspective?
Photo credit: GazetteLive.co.uk
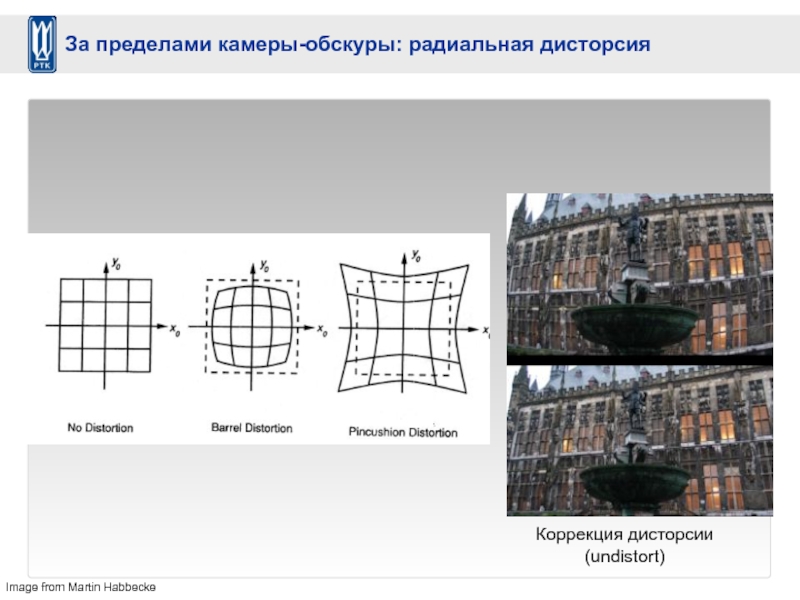
Слайд 49Image from Martin Habbecke
Коррекция дисторсии
(undistort)
За пределами камеры-обскуры: радиальная дисторсия
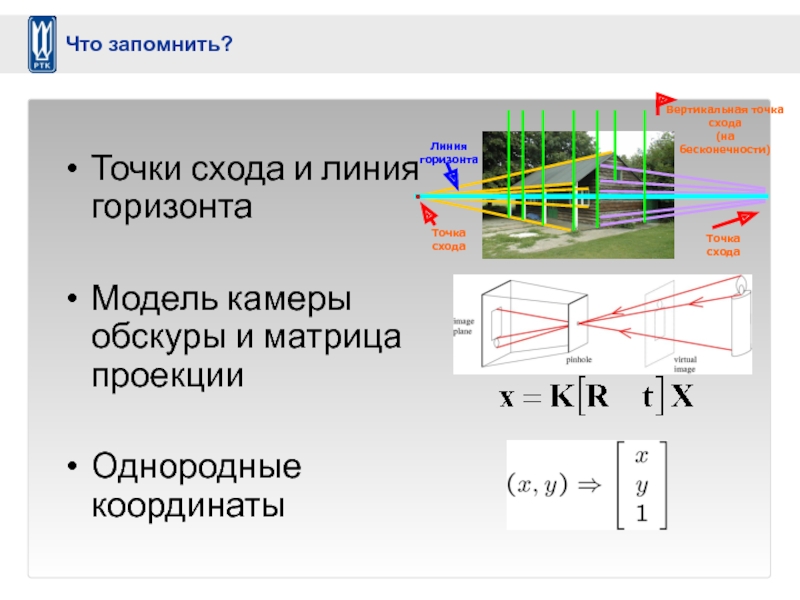
Слайд 50
Точки схода и линия горизонта
Модель камеры обскуры и матрица проекции
Однородные координаты
Что
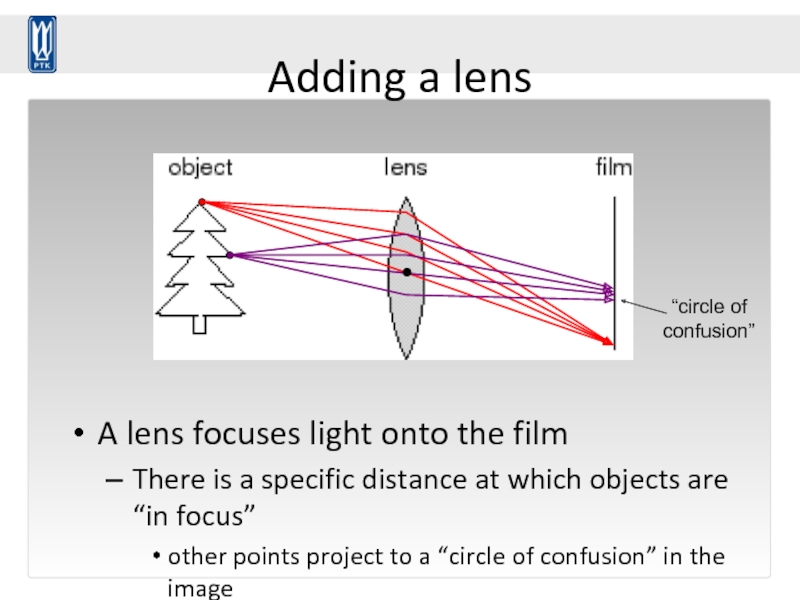
Слайд 52Adding a lens
A lens focuses light onto the film
There is a
other points project to a “circle of confusion” in the image
Changing the shape of the lens changes this distance
Слайд 53Focal length, aperture, depth of field
A lens focuses parallel rays onto
focal point at a distance f beyond the plane of the lens
Aperture of diameter D restricts the range of rays
focal point
F
optical center
(Center Of Projection)
Slide source: Seitz
Слайд 54Depth of field
Changing the aperture size or focal length affects depth
f / 5.6
f / 32
Flower images from Wikipedia http://en.wikipedia.org/wiki/Depth_of_field
Slide source: Seitz
Слайд 55Shrinking the aperture
Why not make the aperture as small as possible?
Less
Diffraction effects
Slide by Steve Seitz
Слайд 57Capturing Light… in man and machine
CS 143: Computer Vision
James Hays, Brown,
Many slides by Alexei A. Efros
Слайд 59A photon’s life choices
Absorption
Diffusion
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
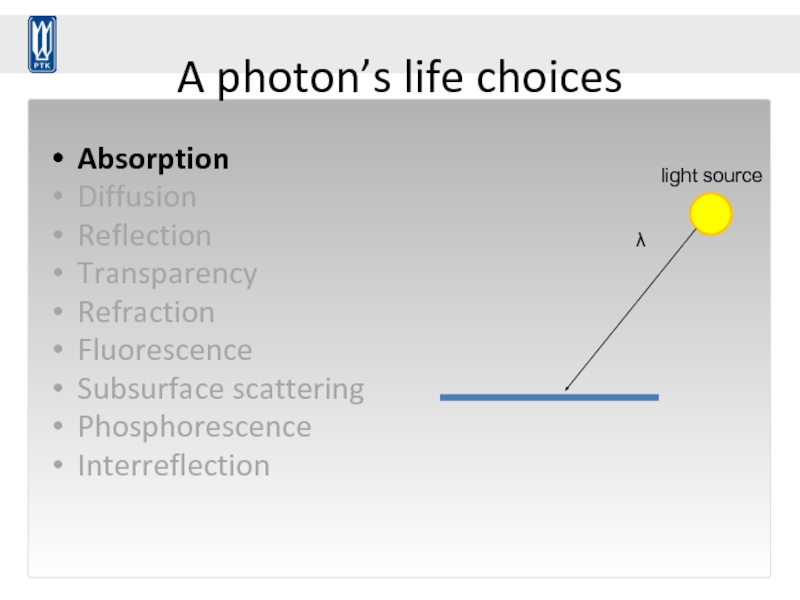
Слайд 60A photon’s life choices
Absorption
Diffusion
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
λ
light source
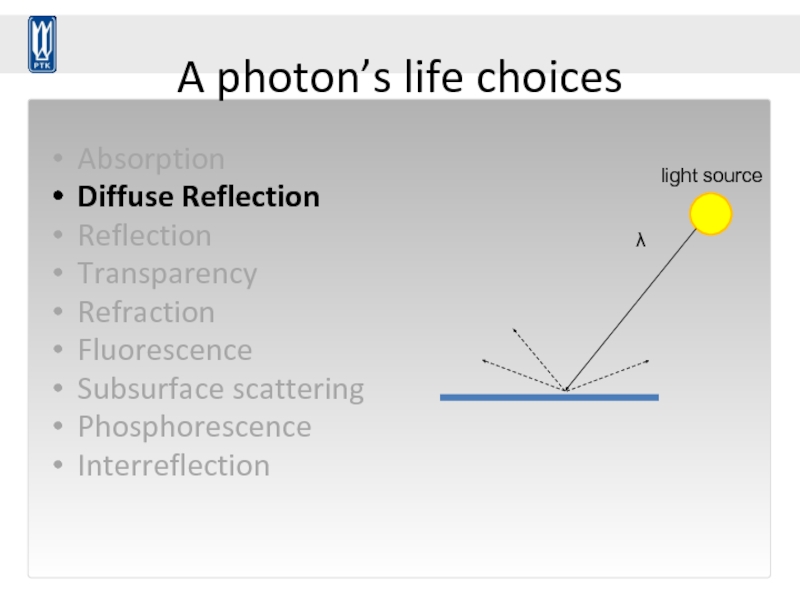
Слайд 61A photon’s life choices
Absorption
Diffuse Reflection
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
λ
light source
Слайд 62A photon’s life choices
Absorption
Diffusion
Specular Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
λ
light source
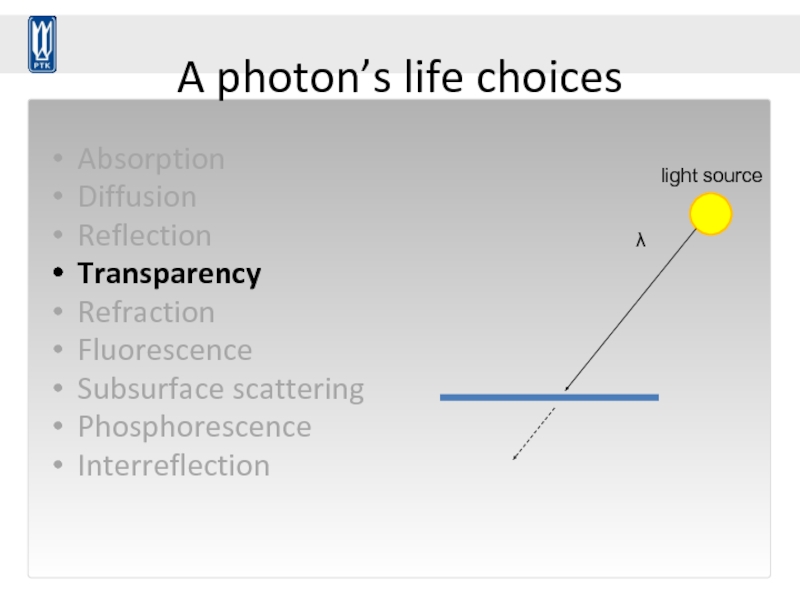
Слайд 63A photon’s life choices
Absorption
Diffusion
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
λ
light source
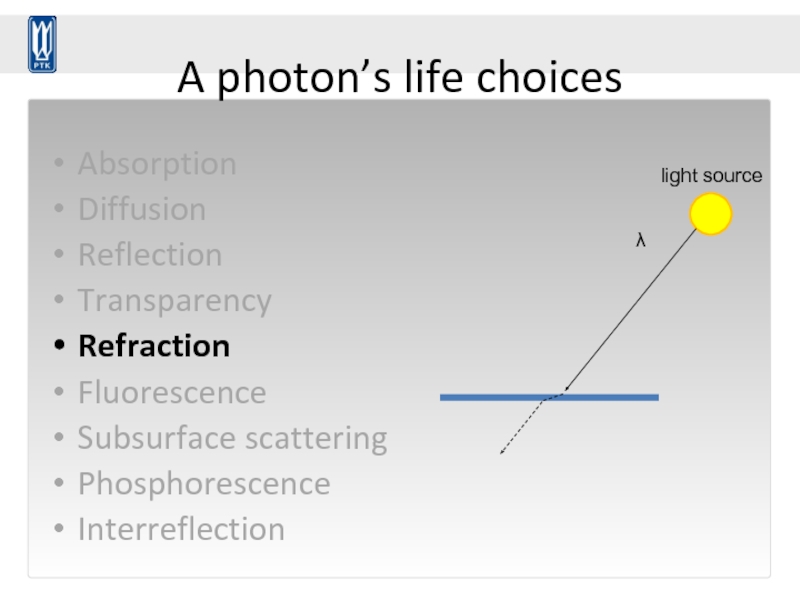
Слайд 64A photon’s life choices
Absorption
Diffusion
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
λ
light source
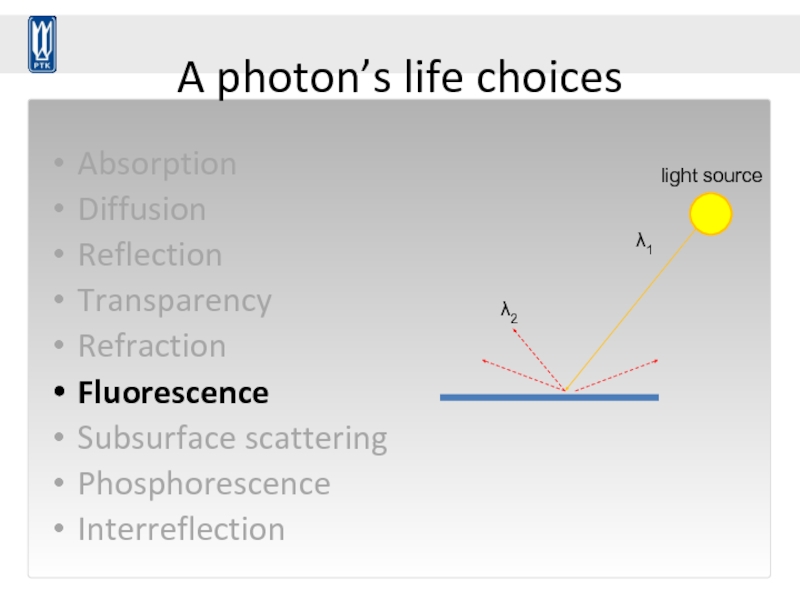
Слайд 65A photon’s life choices
Absorption
Diffusion
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
λ1
light source
λ2
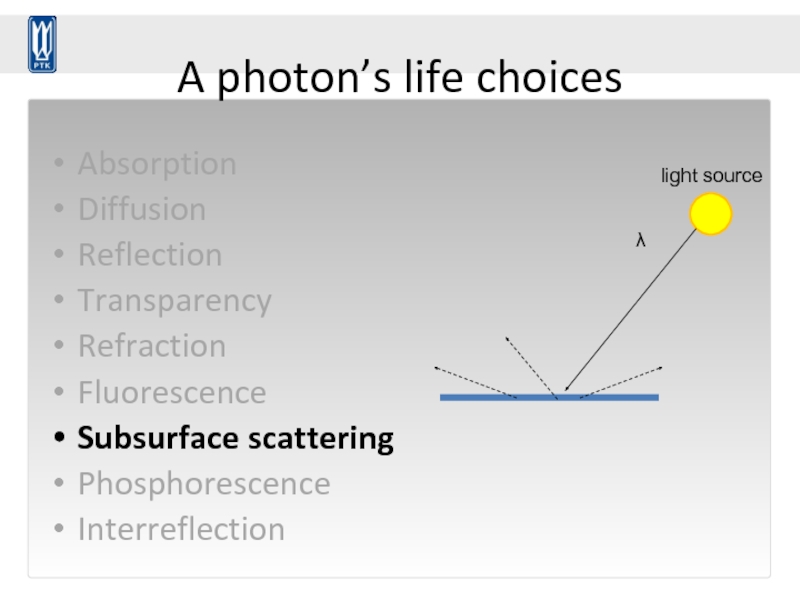
Слайд 66A photon’s life choices
Absorption
Diffusion
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
λ
light source
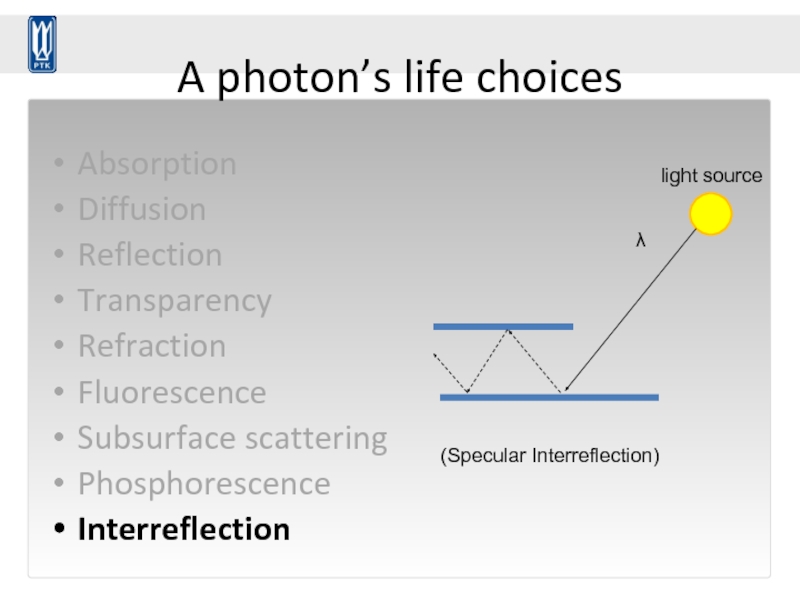
Слайд 67A photon’s life choices
Absorption
Diffusion
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
t=1
light source
t=n
Слайд 68A photon’s life choices
Absorption
Diffusion
Reflection
Transparency
Refraction
Fluorescence
Subsurface scattering
Phosphorescence
Interreflection
λ
light source
(Specular Interreflection)
Слайд 69Lambertian Reflectance
In computer vision, surfaces are often assumed to be ideal
Слайд 71Digital camera
A digital camera replaces film with a sensor array
Each cell
Two common types
Charge Coupled Device (CCD)
CMOS
http://electronics.howstuffworks.com/digital-camera.htm
Slide by Steve Seitz
Слайд 74Interlace vs. progressive scan
http://www.axis.com/products/video/camera/progressive_scan.htm
Slide by Steve Seitz
Слайд 75Progressive scan
http://www.axis.com/products/video/camera/progressive_scan.htm
Slide by Steve Seitz
Слайд 76Interlace
http://www.axis.com/products/video/camera/progressive_scan.htm
Slide by Steve Seitz
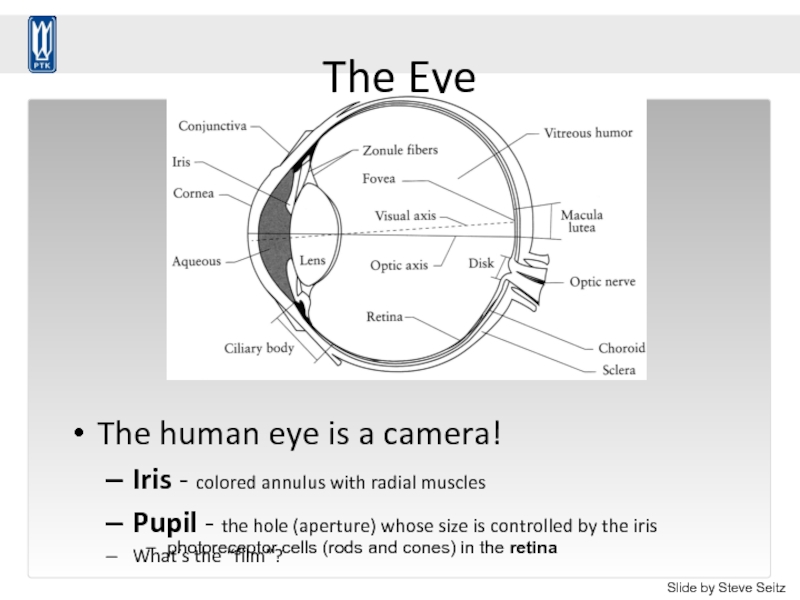
Слайд 78The Eye
The human eye is a camera!
Iris - colored annulus with
Pupil - the hole (aperture) whose size is controlled by the iris
What’s the “film”?
photoreceptor cells (rods and cones) in the retina
Slide by Steve Seitz
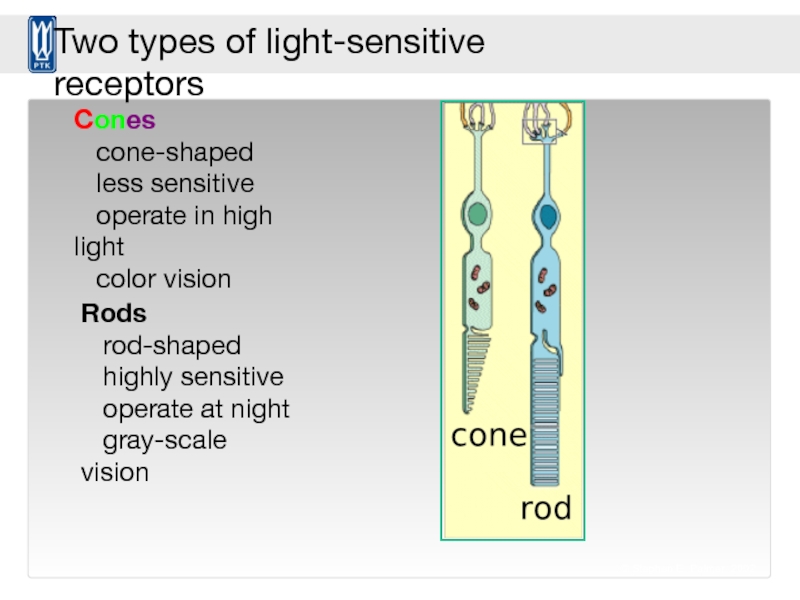
Слайд 82© Stephen E. Palmer, 2002
Cones
cone-shaped
less sensitive
color vision
Two types of light-sensitive receptors
Rods
rod-shaped
highly sensitive
operate at night
gray-scale vision
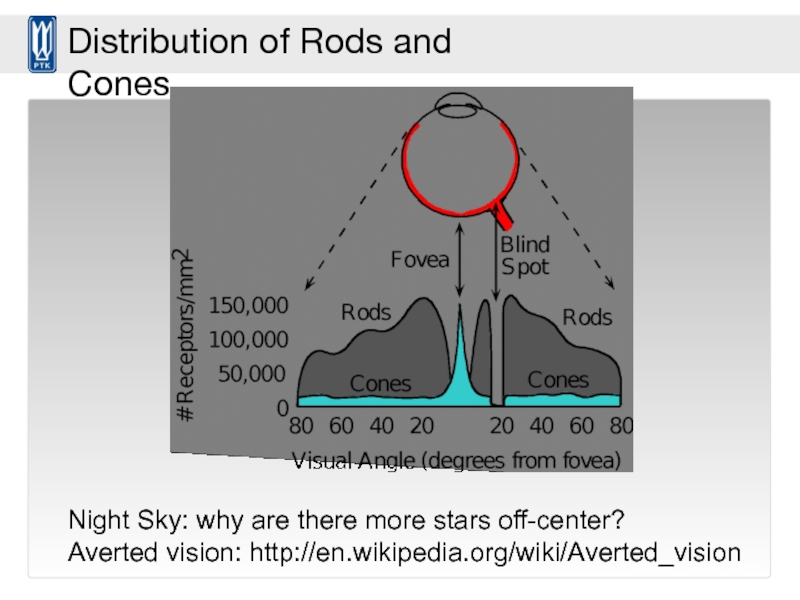
Слайд 84© Stephen E. Palmer, 2002
Distribution of Rods and Cones
Night Sky: why
Слайд 85Eye Movements
Saccades
Can be consciously controlled. Related to perceptual attention.
200ms to initiation,
Microsaccades
Involuntary. Smaller amplitude. Especially evident during prolonged fixation. Function debated.
Ocular microtremor (OMT)
involuntary. high frequency (up to 80Hz), small amplitude.
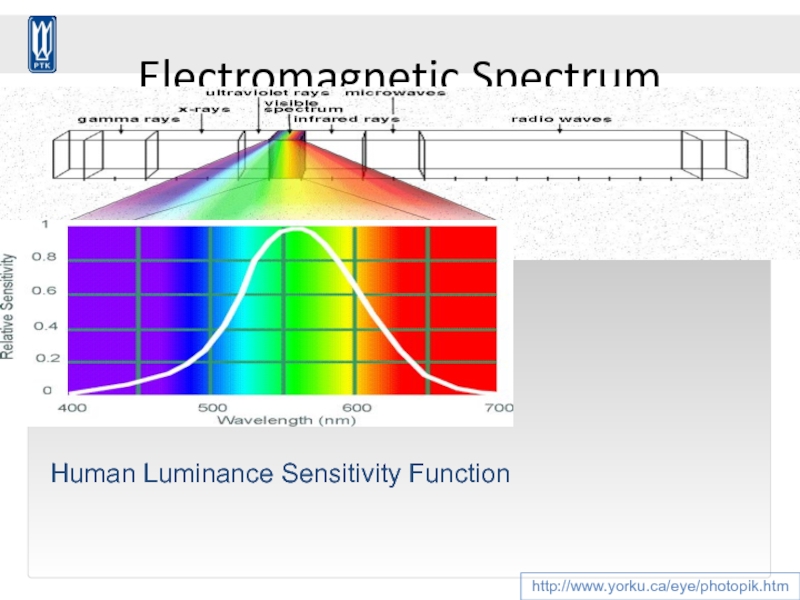
Слайд 86Electromagnetic Spectrum
http://www.yorku.ca/eye/photopik.htm
Human Luminance Sensitivity Function
Слайд 87
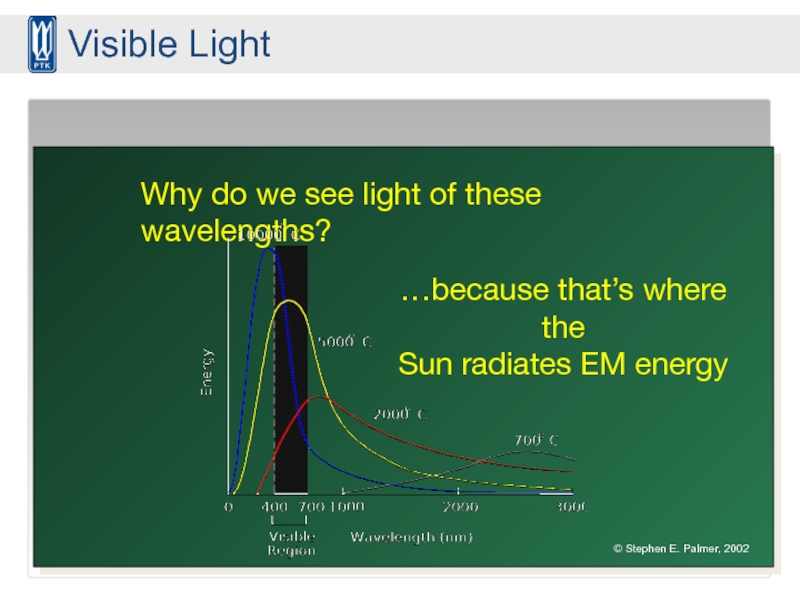
Why do we see light of these wavelengths?
© Stephen E. Palmer,
…because that’s where the
Sun radiates EM energy
Visible Light
Слайд 88The Physics of Light
Any patch of light can be completely described
physically
(per time unit) at each wavelength 400 - 700 nm.
© Stephen E. Palmer, 2002
Слайд 90The Physics of Light
Some examples of the reflectance spectra of surfaces
Wavelength
% Photons Reflected
© Stephen E. Palmer, 2002
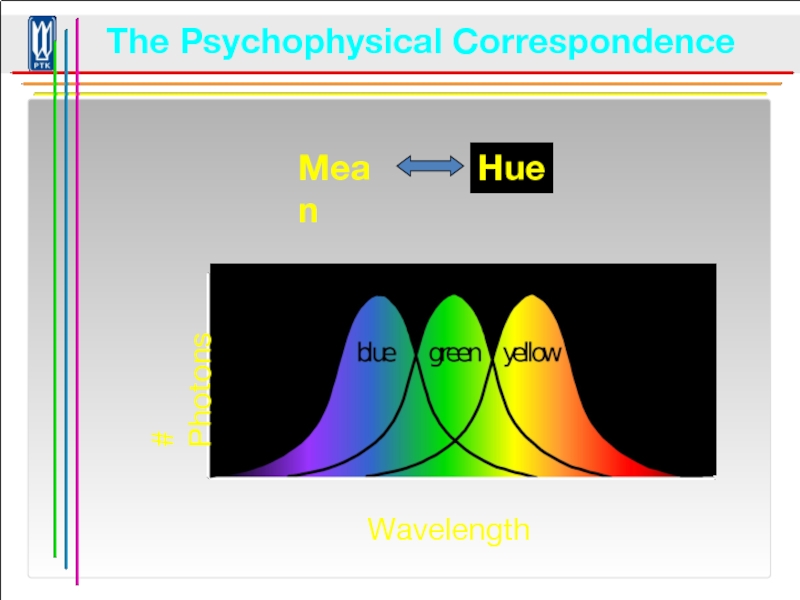
Слайд 91The Psychophysical Correspondence
There is no simple functional description for the perceived
color
A helpful constraint:
Consider only physical spectra with normal distributions
© Stephen E. Palmer, 2002
Слайд 95© Stephen E. Palmer, 2002
Three kinds of cones:
Physiology of Color Vision
Why are there 3?
Слайд 96Impossible Colors
Can you make the cones respond in ways that typical
http://en.wikipedia.org/wiki/Impossible_colors
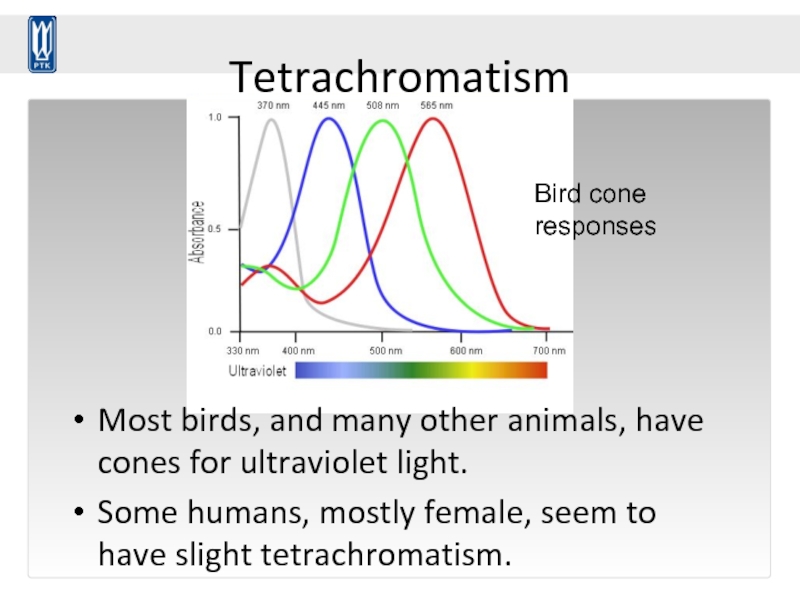
Слайд 97Tetrachromatism
Most birds, and many other animals, have cones for ultraviolet light.
Some
Bird cone responses
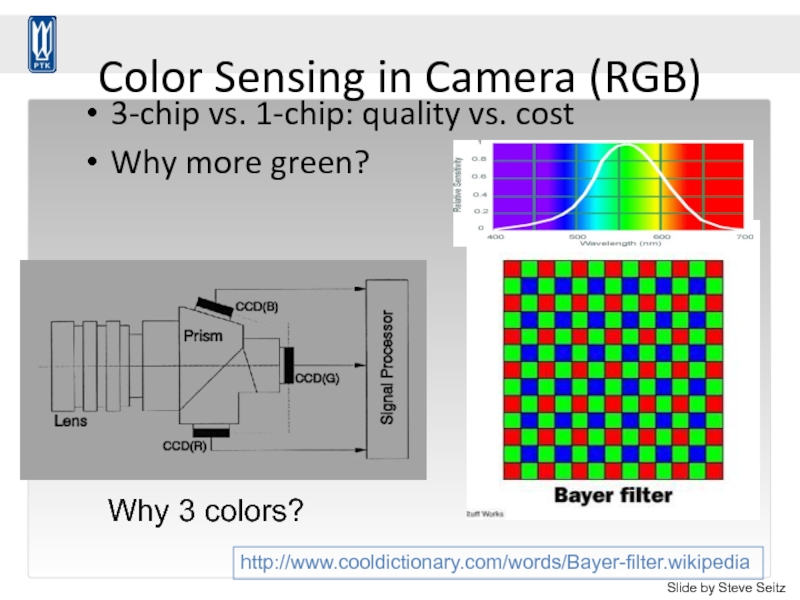
Слайд 99Color Sensing in Camera (RGB)
3-chip vs. 1-chip: quality vs. cost
Why more
http://www.cooldictionary.com/words/Bayer-filter.wikipedia
Why 3 colors?
Slide by Steve Seitz
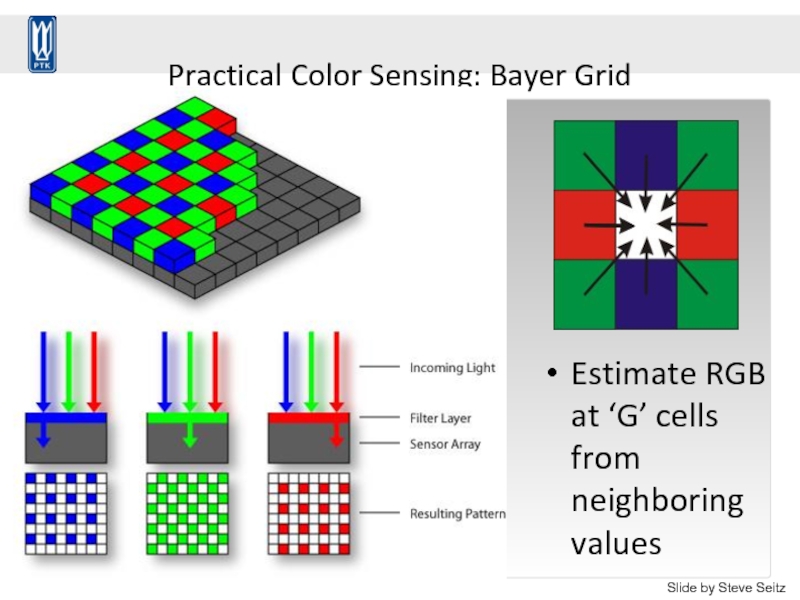
Слайд 100Practical Color Sensing: Bayer Grid
Estimate RGB
at ‘G’ cells from neighboring values
Slide
Слайд 102Images in Matlab
Images represented as a matrix
Suppose we have a NxM
im(1,1,1) = top-left pixel value in R-channel
im(y, x, b) = y pixels down, x pixels to right in the bth channel
im(N, M, 3) = bottom-right pixel in B-channel
imread(filename) returns a uint8 image (values 0 to 255)
Convert to double format (values 0 to 1) with im2double
R
G
B
row
column
Слайд 103Color spaces
How can we represent color?
http://en.wikipedia.org/wiki/File:RGB_illumination.jpg
Слайд 104Color spaces: RGB
Image from: http://en.wikipedia.org/wiki/File:RGB_color_solid_cube.png
Some drawbacks
Strongly correlated channels
Non-perceptual
Default
R
(G=0,B=0)
G
(R=0,B=0)
B
(R=0,G=0)
Слайд 106Color spaces: YCbCr
Y
(Cb=0.5,Cr=0.5)
Cb
(Y=0.5,Cr=0.5)
Cr
(Y=0.5,Cb=05)
Y=0
Y=0.5
Y=1
Cb
Cr
Fast to compute, good for compression, used by TV
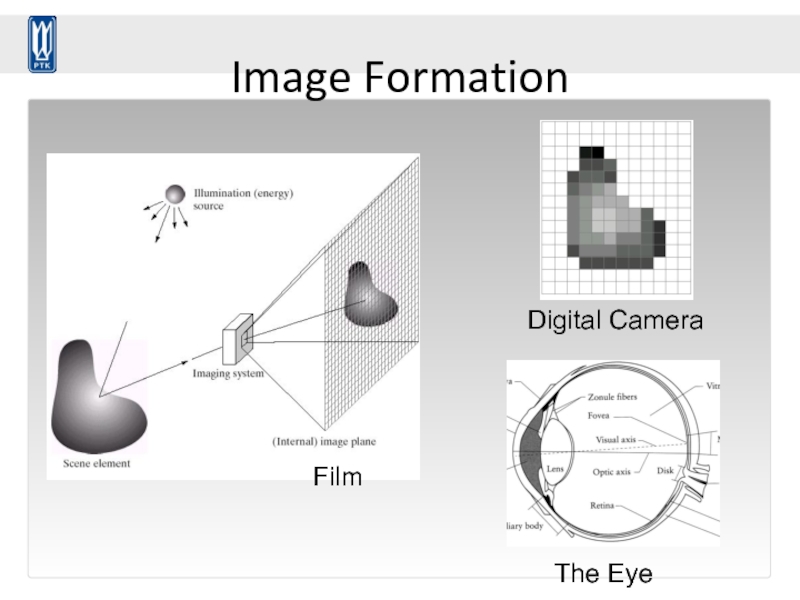
Слайд 114
Восприятие света и цвета
Камера и человеческий глаз
Сенсоры и пиксели
Фильтрация изображений
Практическое задание:
Дальше
Слайд 115Россия, 194064, г. Санкт-Петербург, Тихорецкий пр., 21
тел.: (812) 552-0110 (812) 552-1325
Г О С У Д А Р С Т В Е Н Н Ы Й Н А У Ч Н Ы Й Ц Е Н Т Р Р О С С И И
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ И ОПЫТНО-КОНСТРУКТОРСКИЙ
ИНСТИТУТ РОБОТОТЕХНИКИ И ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ
Г О С У Д А Р С Т В Е Н Н Ы Й Н А У Ч Н Ы Й Ц Е Н Т Р Р О С С И И
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ И ОПЫТНО-КОНСТРУКТОРСКИЙ
ИНСТИТУТ РОБОТОТЕХНИКИ И ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ
Спасибо за внимание!