- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Управление ключами в асимметричных криптосистемах. Лекция 11 презентация
Содержание
- 1. Управление ключами в асимметричных криптосистемах. Лекция 11
- 2. Методы распределения открытых ключей: публичное объявление;
- 3. Авторитетный источник открытых ключей Выполняются следующие действия:
- 4. 3. Инициатор А сохраняет открытый ключ участника
- 5. Сертификаты открытых ключей Каждый сертификат 1. содержит
- 6. 3. Теперь участник А может переслать этот
- 7. Распределение секретных ключей с помощью системы
- 8. Этот протокол уязвим в отношении активных атак.
- 9. 3-х этапный протокол «рукопожатия» 2. Распределение
- 10. 3. Гибридная схема Эта схема предполагает:
- 11. 4. Обмен ключами по схеме Диффи –
- 12. Алгоритм обмена ключами по схеме Диффи-Хеллмана. 1.
- 13. Пример. Обмен ключами строится на использовании простого
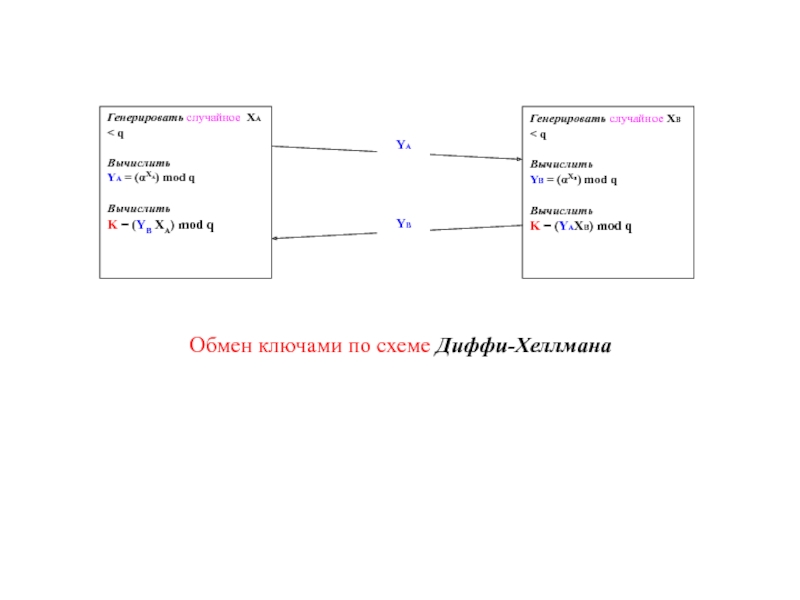
- 14. Обмен ключами по схеме Диффи-Хеллмана
Слайд 1ЛЕКЦИЯ 11.
Управление ключами в асимметричных криптосистемах.
11.1. Распределение открытых ключей.
11.2. Распределение секретных
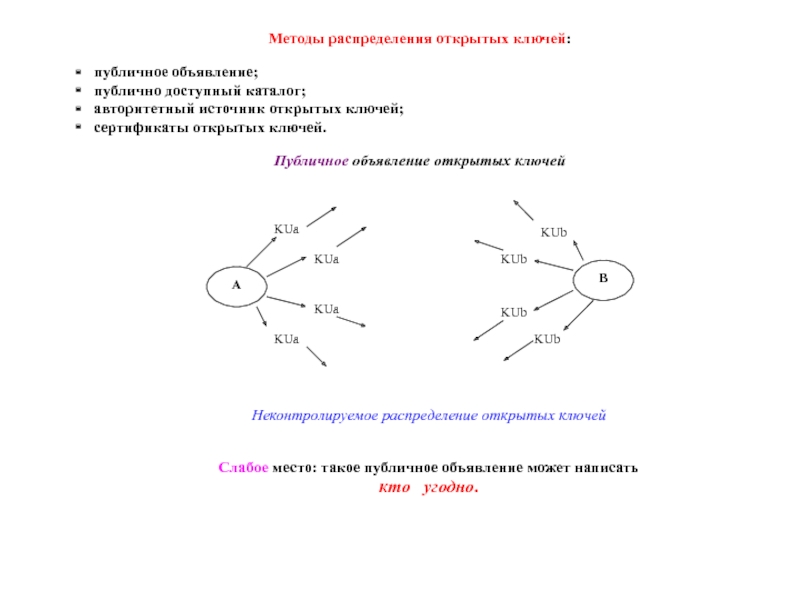
Слайд 2Методы распределения открытых ключей:
публичное объявление;
публично доступный каталог;
авторитетный источник открытых ключей;
сертификаты открытых
Публичное объявление открытых ключей
Неконтролируемое распределение открытых ключей
Слабое место: такое публичное объявление может написать
кто угодно.
Слайд 3Авторитетный источник открытых ключей
Выполняются следующие действия:
Инициатор А посылает сообщение с меткой
Авторитетный источник отвечает сообщением, которое шифруется с использованием личного ключа авторитетного источника KRauth. Это сообщение инициатор А может дешифровать, используя открытый ключ авторитетного источника. Поэтому отправитель А может быть уверенным в том, что сообщение исходит от авторитетного источника. Это сообщение должно включать следующее:
открытый ключ KUb участника В, который участник А может использовать для шифрования сообщений, предназначенных для получателя В;
оригинальный запрос, чтобы сторона А имела возможность сопоставить ответ с ранее отправленным запросом и убедиться, что запрос не был изменен на пути к авторитетному источнику;
оригинальную метку даты/времени, чтобы отправитель А мог удостовериться, что это сообщение не является одним из старых сообщений от авторитетного источника, содержащим ключ, отличный от текущего открытого ключа адресата В.
Слайд 43. Инициатор А сохраняет открытый ключ участника В и использует его
4, 5. Респондент В получает открытый ключ А от авторитетного источника точно таким же способом, каким отправитель А получил открытый ключ получателя В.
К этому моменту открытые ключи оказываются доставленными участникам А и В вышеописанной защищенной процедурой, так что теперь они могут начать постепенный обмен данными.
Но перед этим желательно выполнить два следующих дополнительных действия.
6. Респондент В посылает сообщение инициатору А, шифрованное с помощью KUa и содержащее оказию отправителя А (N1), а также новую оказию, сформированную участником В (N2). Ввиду того, что только он мог дешифровать сообщение (3), присутствие N1 в сообщении (6) убеждает участника А в том, что отправителем полученного сообщения был В.
7. Инициатор А возвращает N2, шифрованное с помощью открытого ключа KUb участника В, чтобы тот мог убедиться в том, что отправителем ответа является А.
Обе стороны могут сохранять открытые ключи друг друга для дальнейшего пользования, что обычно называется кэшированием.
Каталог имен и открытых ключей, поддерживаемый авторитетным источником, остается уязвимым по отношению к вмешательству с неблагоприятными намерениями.
Слайд 5Сертификаты открытых ключей
Каждый сертификат
1. содержит открытый ключ и другую информацию,
2.
3. выдается участнику вместе с соответствующим личным ключом.
Требования к данной схеме:
Любой участник должен иметь возможность прочитать сертификат, чтобы определить имя и открытый ключ владельца сертификата.
Любой участник должен иметь возможность проверить, что сертификат исходит из авторитетного источника сертификатов и не является подделкой.
Только авторитетный источник сертификатов должен иметь возможность создавать и изменять сертификаты.
Любой участник должен иметь возможность проверить срок действия сертификата.
Схема использования сертификатов включает операции:
1. Каждый участник обращается к авторитетному источнику сертификатов, предоставляя открытый ключ и запрашивая для него сертификат.
Запрос должен предполагать либо личное обращение, либо некоторую защищенную форму связи.
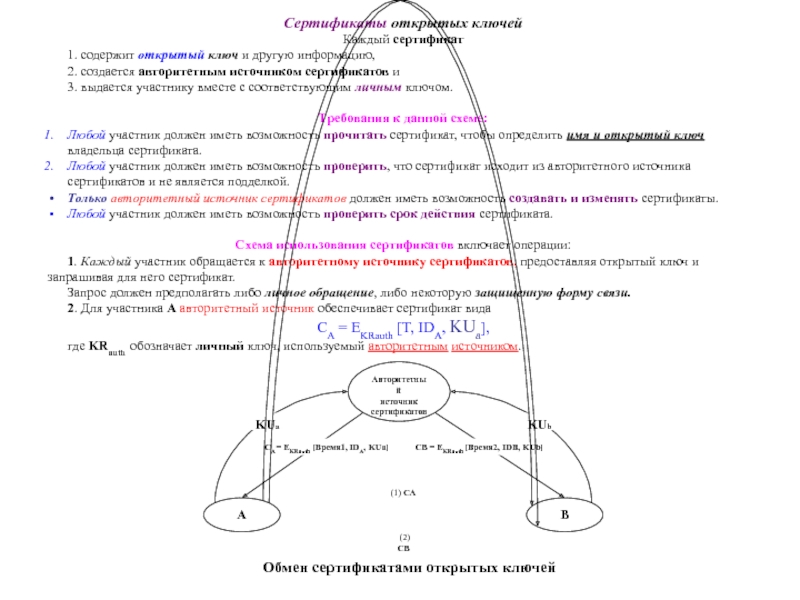
2. Для участника А авторитетный источник обеспечивает сертификат вида
CA = EKRauth [T, IDA, KUa],
где KRauth обозначает личный ключ, используемый авторитетным источником.
Обмен сертификатами открытых ключей
Слайд 63. Теперь участник А может переслать этот сертификат любому другому участнику,
DKUauth [CA] = DKUauth [EKRauth [T, IDA, KUa]] = (T, IDA, KUa).
4. Получатель использует открытый ключ авторитетного источника сертификатов KUauth, чтобы дешифровать сертификат.
А) Ввиду того, что сертификат можно прочитать только с помощью открытого ключа авторитетного источника сертификатов, есть гарантия того, что сертификат пришел именно от авторитетного источника сертификатов.
Б) Элементы IDA и KUa сообщают получателю имя и открытый ключ владельца сертификата.
В) Наконец, метка даты/времени T определяет срок действия сертификата.
Метка даты/времени должна быть защищена от следующей последовательности действий.
1. Противник узнает личный ключ А. По этой причине А генерирует вторую пару ключей (личный и открытый) и обращается к авторитетному источнику сертификатов за новым сертификатом.
2. Тем временем, противник воспроизводит сообщение со старым сертификатом и отсылает его В. Если В будет шифровать сообщения, используя старый скомпрометированный открытый ключ, противник сможет прочитать эти сообщения.
Таким образом, метка даты/времени является чем-то вроде даты истечения срока действия.
Если сертификат оказывается выданным достаточно давно, предполагается, что срок его действия истек.
Слайд 7 Распределение секретных ключей с помощью системы с открытым ключом
1. Простое
Простое использование шифрования с открытым ключом при выборе сеансового ключа
Для этого предполагается следующая процедура:
Сторона А генерирует пару открытый/личный ключи {KUa, KRa} и передает сообщение стороне В, содержащее KUa и идентификатор IDA отправителя А.
Получатель В генерирует секретный ключ Ks и передает этот ключ инициатору сообщения А зашифрованным с помощью открытого ключа KUa инициатора А.
Пользователь А вычисляет DKRa[EKUa[Ks]], чтобы восстановить секретный ключ. Поскольку только пользователь А может дешифровать это сообщение, только участники обмена данными А и В будут знать значение Ks.
Участник А выбрасывает ключ KRa , а участник В – выбрасывает ключ KUa.
Слайд 8Этот протокол уязвим в отношении активных атак.
Противник Е, имея возможность внедрения
Участник А генерирует пару
открытый/личный ключи {KUa, KRa}
и передает сообщение стороне В, содержащее KUa и идентификатор IDA отправителя А.
2. Противник Е перехватывает сообщение, создает собственную пару
открытый/личный ключи {KUе, KRе}
и передает сообщение адресату В, содержащее KUе ||IDA.
3. В генерирует секретный ключ Ks и передает EKUе[Ks].
4. Противник Е перехватывает это сообщение и узнает Ks, вычисляя DKRe[EKUе[Ks]].
5. Противник Е передает участнику А сообщение EKUa[Ks].
Слайд 9
3-х этапный протокол «рукопожатия»
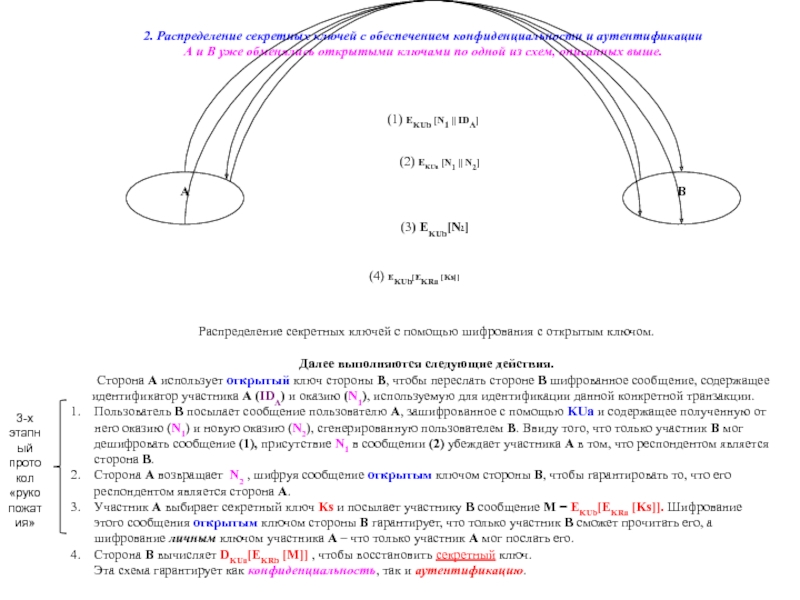
2. Распределение секретных ключей с обеспечением конфиденциальности и
А и В уже обменялись открытыми ключами по одной из схем, описанных выше.
Распределение секретных ключей с помощью шифрования с открытым ключом.
Далее выполняются следующие действия.
Сторона А использует открытый ключ стороны В, чтобы переслать стороне В шифрованное сообщение, содержащее идентификатор участника А (IDA) и оказию (N1), используемую для идентификации данной конкретной транзакции.
Пользователь В посылает сообщение пользователю А, зашифрованное с помощью KUa и содержащее полученную от него оказию (N1) и новую оказию (N2), сгенерированную пользователем В. Ввиду того, что только участник В мог дешифровать сообщение (1), присутствие N1 в сообщении (2) убеждает участника А в том, что респондентом является сторона В.
Сторона А возвращает N2 , шифруя сообщение открытым ключом стороны В, чтобы гарантировать то, что его респондентом является сторона А.
Участник А выбирает секретный ключ Ks и посылает участнику В сообщение M = EKUb[EKRa [Ks]]. Шифрование этого сообщения открытым ключом стороны В гарантирует, что только участник В сможет прочитать его, а шифрование личным ключом участника А – что только участник А мог послать его.
Сторона В вычисляет DKUa[EKRb [M]] , чтобы восстановить секретный ключ.
Эта схема гарантирует как конфиденциальность, так и аутентификацию.
Слайд 103. Гибридная схема
Эта схема предполагает:
1. участие центра распределения ключей (ЦРК), с
2. и распределение секретных сеансовых ключей, шифруемых главным ключом.
Схема шифрования с открытым ключом служит для распределения
главных ключей.
В основе трехуровневого подхода лежат следующие соображения.
Скорость выполнения процедуры. Распределение сеансовых ключей с помощью схемы с открытым ключом могло бы сделать производительность системы слишком низкой из-за относительно высоких требований к вычислительным ресурсам при шифровании и дешифровании по такой схеме. В случае трехуровневой иерархии шифрование с открытым ключом применяется лишь иногда, чтобы изменить главный ключ, разделяемый пользователем и ЦРК.
Обратная совместимость. Гибридную схему можно легко реализовать в виде расширения уже имеющейся схемы, предполагающей использование ЦРК, с минимальными изменениями предусмотренной процедуры и программного обеспечения.
Слайд 114. Обмен ключами по схеме Диффи – Хеллмана
Алгоритм ограничивается процедурой обмена
Дискретный логарифм можно определить следующим образом:
1. Сначала определяется первообразный корень простого числа p - если a является первообразным корнем простого числа p, то все числа
a mod p , (a2) mod p, …, (ap-1) mod p
должны быть разными и представлять все целые числа от 1 до p-1 в некоторой перестановке.
2. Для любого целого числа b и любого первообразного корня a простого числа p однозначно определяется показатель степени i, при котором
b = (ai) mod p, где 0 ≤ i ≤ (p-1).
Этот показатель степени обычно называется дискретным логарифмом, или индексом b по основанию a , рассматриваемым по модулю p.
Это значение записывается в форме ind a,p(b).
Слайд 12Алгоритм обмена ключами по схеме Диффи-Хеллмана.
1. В схеме имеются два открытых
простое число q и целое число α, являющееся первообразным корнем q.
2. Пользователь А выбирает целое число XA < q и вычисляет
YA = (α XA) mod q.
3. Пользователь В независимо выбирает случайное целое число XB < q и вычисляет
YB = (αXB) mod q.
4. Каждая сторона сохраняет значение X в тайне и делает значение Y свободно доступным другой стороне.
5. Пользователь А вычисляет ключ по формуле
K = (YB
XA) mod q,
6. А пользователь В – по формуле
K = (YA
XB) mod q.
Эти две формулы вычисления дают одинаковые результаты, как показано ниже.
K = (YB XA) mod q =
= (((αXB) mod q) XA) mod q =
= ((αXB) XA) mod q =
= ((αXB XA) mod q =
= ((αXA) XB) mod q =
= (((αXA) mod q) XB) mod q =
= (YA XB) mod q.
Итак, обе стороны обменялись секретным ключом.
Противнику придется работать только с q, α, YA и YB и вычислять дискретный логарифм, чтобы определить ключ.
Например, чтобы определить ключ пользователя В, противнику нужно вычислить
XB = inda,q (YB).
После этого он сможет вычислить ключ К точно так же, как это делает пользователь В.
Слайд 13Пример.
Обмен ключами строится на использовании простого числа q = 97 и
1. Пользователи А и В выбирают секретные ключи
XA = 36 и XB = 58 соответственно.
2. Каждый вычисляет свой открытый ключ:
YA = 536 = 50 mod 97,
YB = 558 = 44 mod 97.
3. После того как пользователи обменялись открытыми ключами, каждый из них может вычислить общий секретный ключ:
K = (YB
XA) mod 97 = 44
36 = 75 mod 97,
K = (YA
XB) mod 97 = 50
58 = 75 mod 97.
Имея {50, 44}, противнику не удастся с легкостью вычислить 75.
Глобальные открытые элементы
q - простое число
α - первообразный корень q, α < q
Вычисление ключа пользователем А
Выбор секретного XA XA < q
Вычисление YA YA = (αXA) mod q
Вычисление ключа пользователем В
Выбор секретного XB XB < q
Вычисление YB YB = (αXB) mod q
Вычисление секретного ключа пользователем А
K = (YBXA) mod q
Вычисление секретного ключа пользователем B
K = (YAXB) mod q
Алгоритм обмена ключами по схеме Диффи-Хеллмана