- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 3. Арифметические основы ЭВМ презентация
Содержание
- 1. Тема 3. Арифметические основы ЭВМ
- 3. Непозиционная система счисления -римская система. В качестве
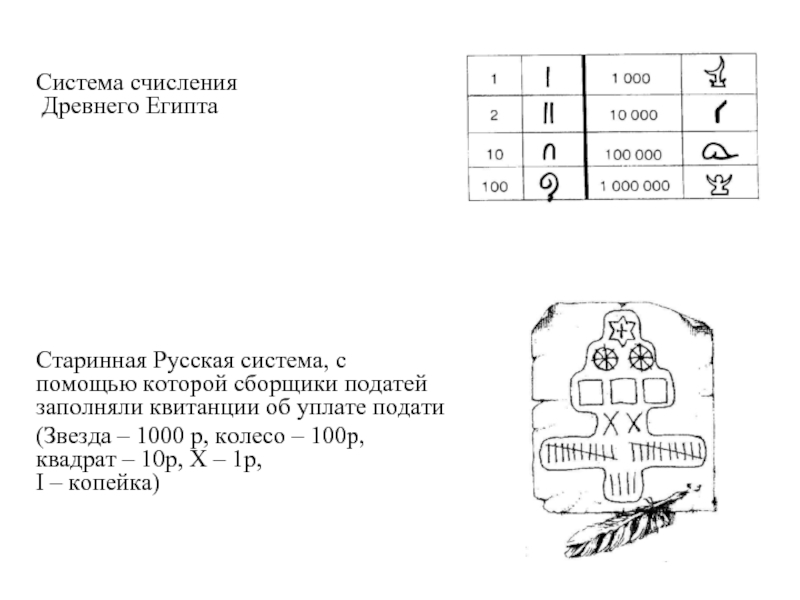
- 4. Система счисления Древнего Египта
- 5. Славянская нумерация (или алфавитная) – числовые значения
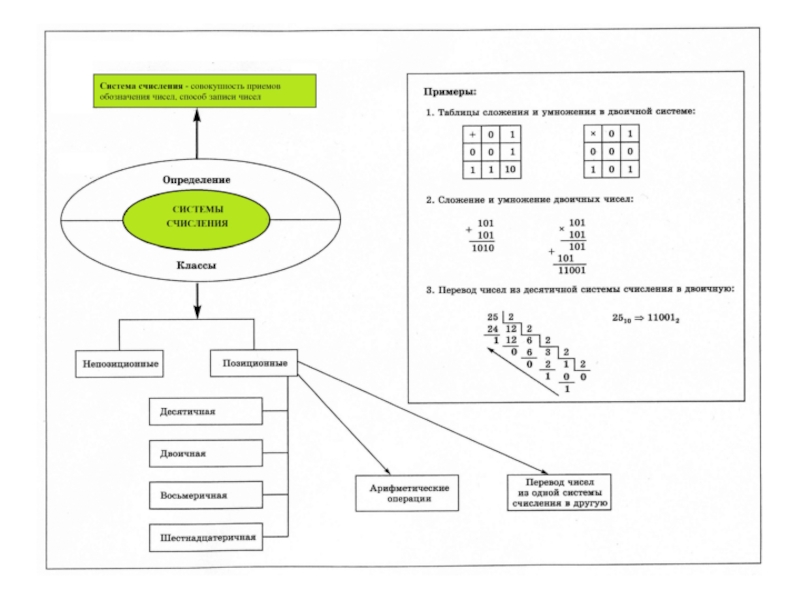
- 6. В позиционной СС количественное значение каждой
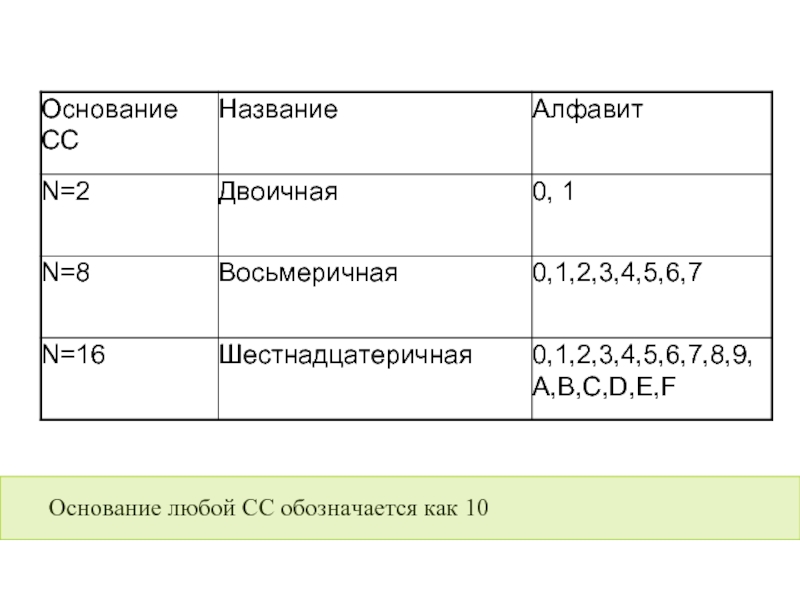
- 7. Основание любой СС обозначается как 10
- 8. Развернутая форма записи числа: Aq=an-1qn-1+ an-2qn-2... +a1q+a0+a-1q-1+a-2q-2+...+
- 9. Пример 3. Получить развернутую запись чисел: 26,
- 10. Системы счисления по основанию 2: двоичная (используются
- 11. Пример. Перевести десятичное число в двоичную систему
- 12. Пример. Перевести десятичное число 567 в шестнадцатеричную СС
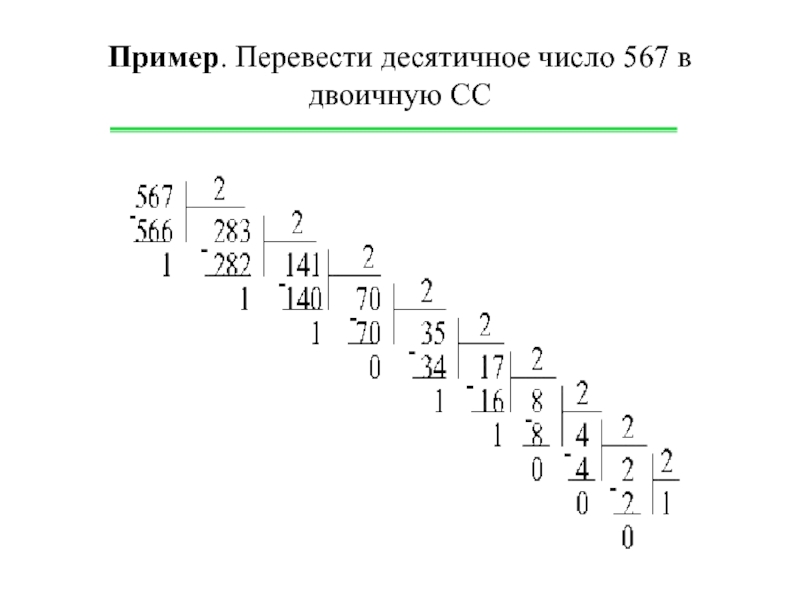
- 13. Пример. Перевести десятичное число 567 в двоичную СС
- 14. Пример. Перевести десятичную дробь 0,1875 в двоичную,
- 15. 3. Переводы чисел в смешанных системах счисления
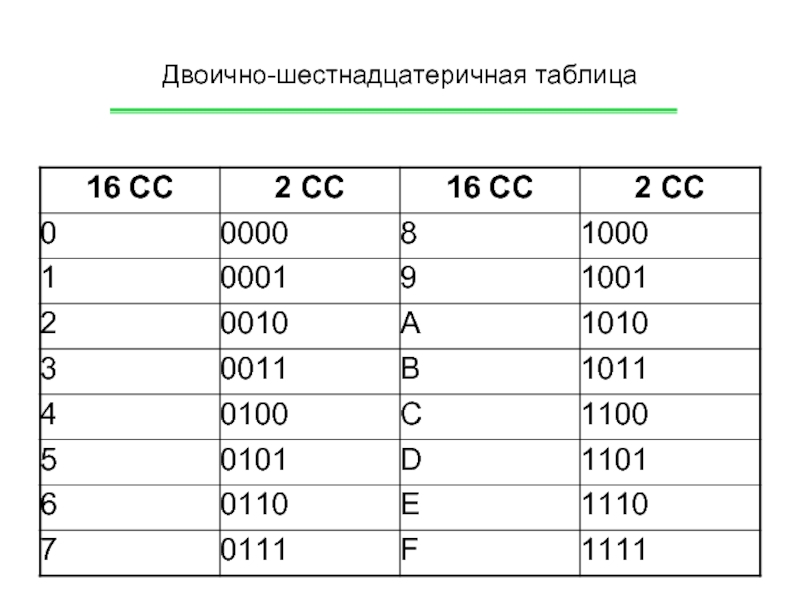
- 16. Двоично-шестнадцатеричная таблица
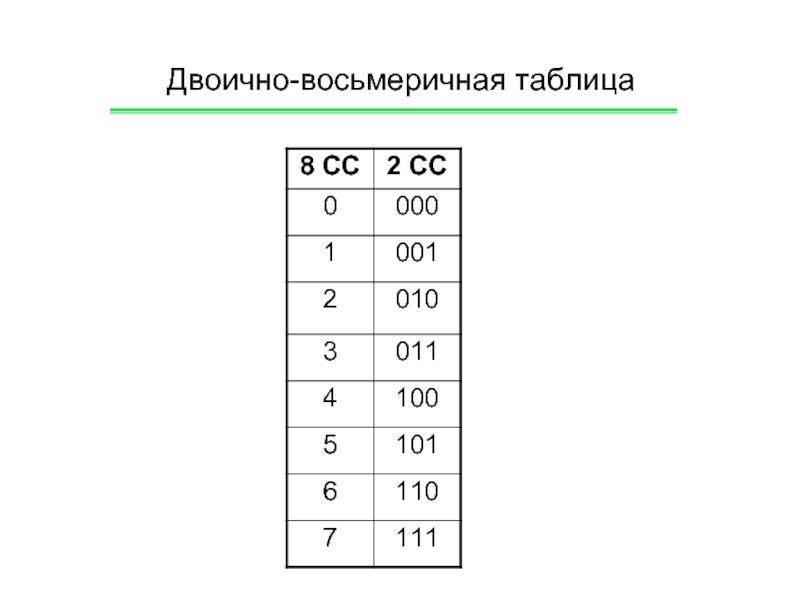
- 17. Двоично-восьмеричная таблица
- 18. Пример. Перевести двоичное число 110111101011101111 в шестнадцатеричную
- 19. Пример. Перевести число 15FC16 в двоичную систему.
- 20. Пример. Перевести смешанное число 1011101,101112 в восьмеричную
- 21. Арифметика в позиционных системах счисления
- 22. Пример. Сложить числа 100000001002 + 1110000102 =
Слайд 1Тема 3. Арифметические основы ЭВМ
Понятие о системах счисления
Системы счисления, используемые в
Переводы чисел в смешанных системах счисления
Арифметика в позиционных системах счисления
Слайд 3Непозиционная система счисления -римская система. В качестве цифр используются латинские буквы:
I V X L C D M
1 5 10 50 100 500 1000
Пример
Пример 2. MCMXCVIII = 10000 + (-100 + 1000) + (-10 + 100) + 5 + 1+1+1 = 1998.
1. Понятие о системах счисления
Слайд 4
Система счисления
Древнего Египта
Старинная Русская система, с помощью которой сборщики
(Звезда – 1000 р, колесо – 100р, квадрат – 10р, Х – 1р, I – копейка)
Слайд 5Славянская нумерация (или алфавитная) – числовые значения букв устанавливались в порядке
Над буквой, обозначающей число, ставился специальный знак ~ («титло»).
Славянская система счисления сохранилась в церковных книгах.
Слайд 6
В позиционной СС количественное значение каждой цифры зависит от ее места
Древнее написание цифр (количество углов = значению символа)
Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр.
При n<10 используют n первых арабских цифр.
При n>10 к десяти арабским цифрам добавляют буквы.
Слайд 8
Развернутая форма записи числа:
Aq=an-1qn-1+ an-2qn-2... +a1q+a0+a-1q-1+a-2q-2+...+ a-m q-m
здесь ai – коэффициенты (цифры числа),
q – снование системы счисления (q>1),
n – число разрядов целой части числа, m – число разрядов дробной части числа.
Слайд 9Пример 3. Получить развернутую запись чисел:
26, 38710=2⋅101 + 6⋅100 + 3
1011012 = 1⋅10101 + 0⋅10100 + 1⋅1011 + 1⋅1010+ 0⋅101 + 1 ⋅ 100
15FC16 = 1 ⋅ 103 + 5 ⋅ 102 + F ⋅ 101 + C ⋅ 100
Пример 4. Перевести в десятичную систему.
1011012 = 1 ⋅ 25 + 0 ⋅ 24 + 1 ⋅ 23 + 1 ⋅ 22+ 0 ⋅ 21 + 1 ⋅ 20 = 4510
15FC16 = 1 ⋅ 163 + 5 ⋅ 162 + 15 ⋅ 161 + 12 ⋅ 160 = 562810
Слайд 10Системы счисления по основанию 2:
двоичная (используются цифры 0, 1);
восьмеричная (используются цифры
шестнадцатеричная (0, 1, …, 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A< B, C, D, E, F).
2. Системы счисления, используемые в ЭВМ
Достоинства двоичной системы:
для реализации нужны технические устройства с двумя устойчивыми состояниями;
представление информации посредством двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
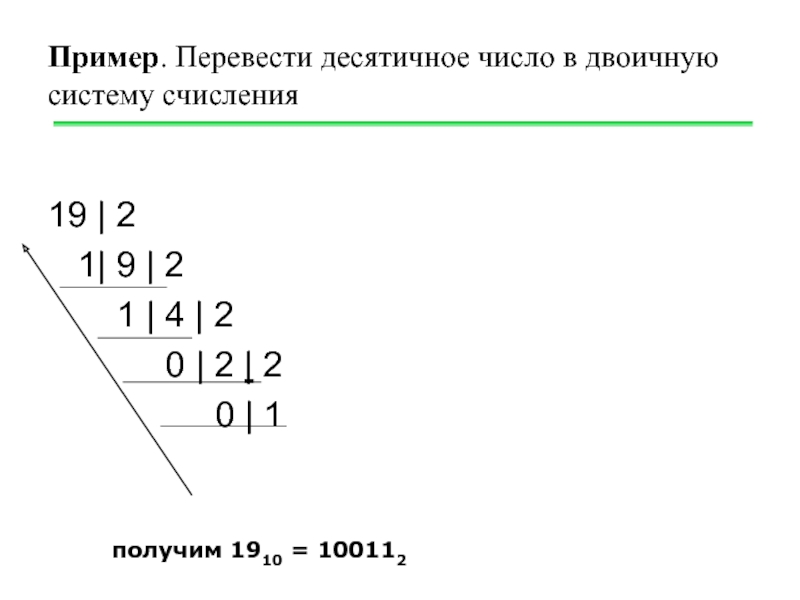
Слайд 11Пример. Перевести десятичное число в двоичную систему счисления
19 | 2
1 | 4 | 2
0 | 2 | 2
0 | 1
получим 1910 = 100112
Слайд 14Пример. Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы
0 1875 0 1875 0 1875
*2 *8 *16
0 3750 1 5000 1 1250
*2 *8 1 875
0 7500 4 0000 3 0000
*2
1 5000
*2
1 0000
0,187510 = 0,00112 = 0.148 = 0,3 16
Слайд 18Пример. Перевести двоичное число 110111101011101111 в шестнадцатеричную систему.
Разделим число на группы
0011 0111 1010 1110 1111.
Теперь заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру.
0011 0111 1010 1110 11112 = 37AEF16.
Слайд 19Пример. Перевести число 15FC16 в двоичную систему.
Каждую цифру в шестнадцатеричном
Получим:
0001 0101 1111 1100.
Отбросим нули слева и получим результат в двоичной системе счисления.
15FC16 = 10101111111002
Слайд 20Пример. Перевести смешанное число 1011101,101112 в восьмеричную систему.
Группы по три двоичных
1011101,101112 = 001 011 101, 101 110 = 135,568.
Слайд 21
Арифметика в позиционных системах счисления
Сложение в двоичной системе счисления осуществляется по
0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10 = 102 (единица идет в старший разряд).
2. Таблица вычитания в двоичной системе счисления имеет вид
0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (единицу забираем у старшего разряда).
3. Таблица умножения в двоичной системе счисления имеет вид
0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1.
4. Таблица деления в двоичной системе счисления имеет вид
0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0,
1 : 1 = 1.
Слайд 22Пример. Сложить числа
100000001002 + 1110000102 = 101110001102
223,28 + 427,548 = 652,748
3B3,616
10000000100 223,2 3B3,6
+ 111000010 +457,54 +38B,4
10111000110 652,74 73E,A
Пример. Выполнить вычитание
1100000011,0112 – 101010111,12 = 110101011,1112
1510,28 - 1230,548 = 257,448
27D,D816 – 191,216 = EC,B816