- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Технологии проектирования информационных систем. Применение сетей Петри для моделирования бизнес-процессов презентация
Содержание
- 1. Технологии проектирования информационных систем. Применение сетей Петри для моделирования бизнес-процессов
- 2. Методы стадии предпроектного обследования методы изучения и
- 3. Учет времени при моделировании систем имеет следующие
- 4. Основные элементы сети Петри Условие (Позиция)
- 5. Модель сети Петри N = (P, T,
- 6. Динамическая модель сети Петри Динамические свойства сети
- 7. Свойства сети Петри Безопасность. Позиция называется безопасной,
- 8. Свойства сети Петри Ограниченность. Позиция называется К-
- 9. Срабатывание перехода Срабатывание перехода – неделимое действие,
- 10. Правила срабатывания переходов Правило 1. Разрешение срабатывания.
- 11. Переход разрешен. Переход не разрешен.
- 12. Правила срабатывания переходов Правило 2. Перемещение фишек.
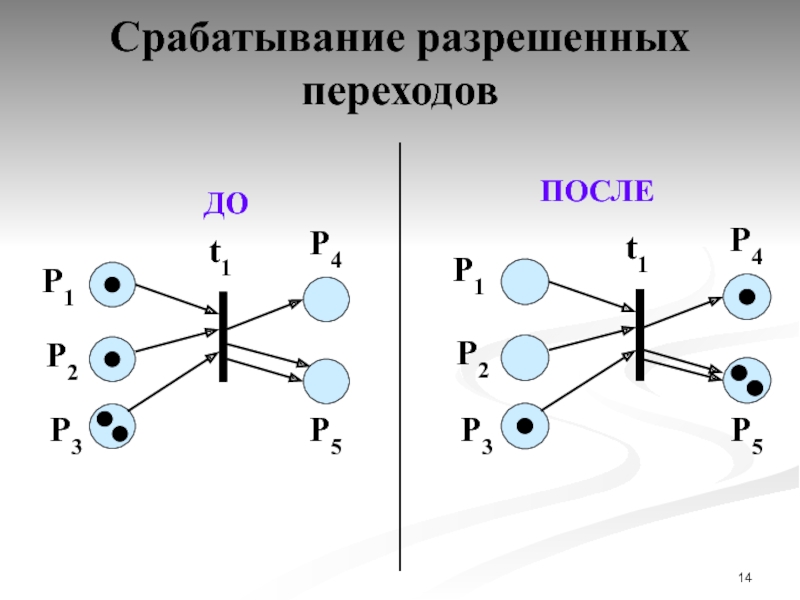
- 13. Срабатывание разрешенных переходов
- 14. Срабатывание разрешенных переходов
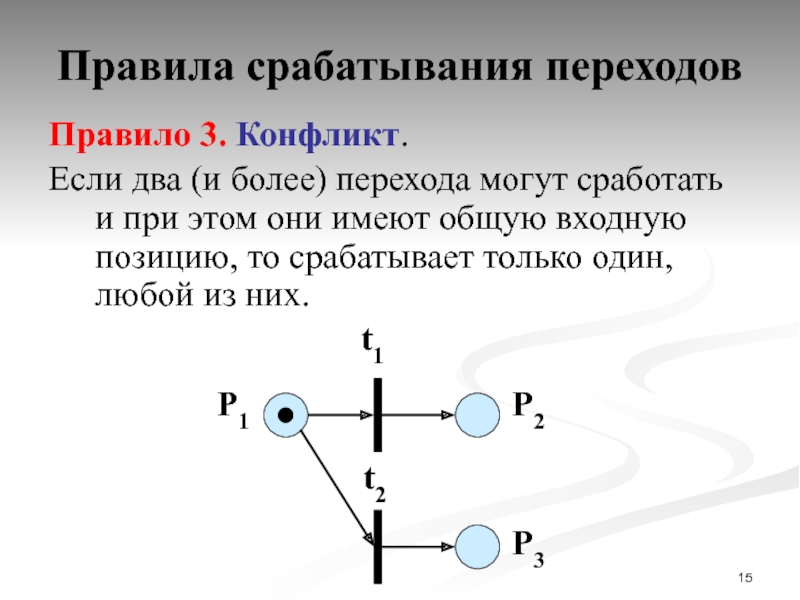
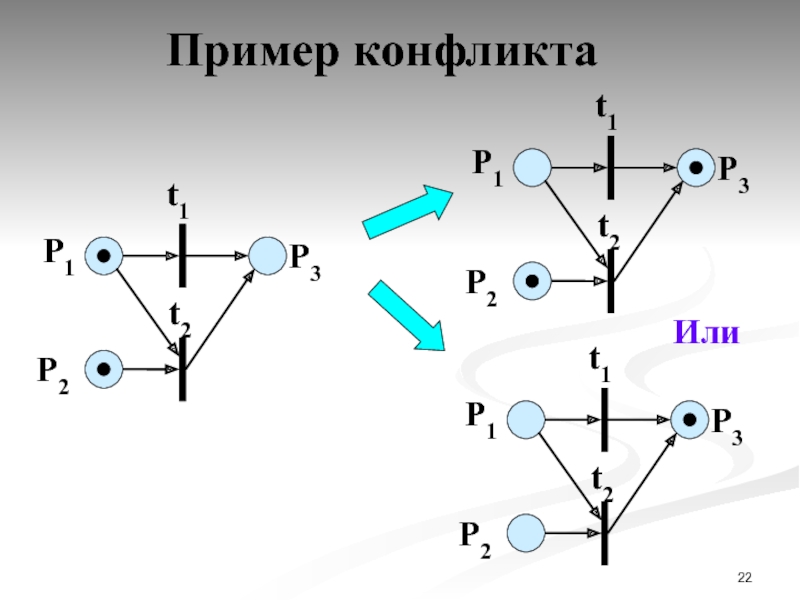
- 15. Правила срабатывания переходов Правило 3. Конфликт.
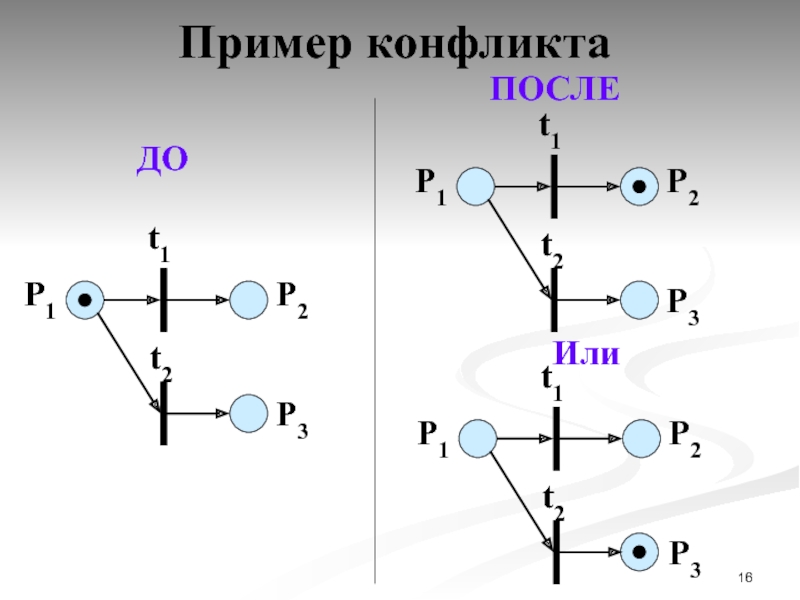
- 16. Пример конфликта P1 P2
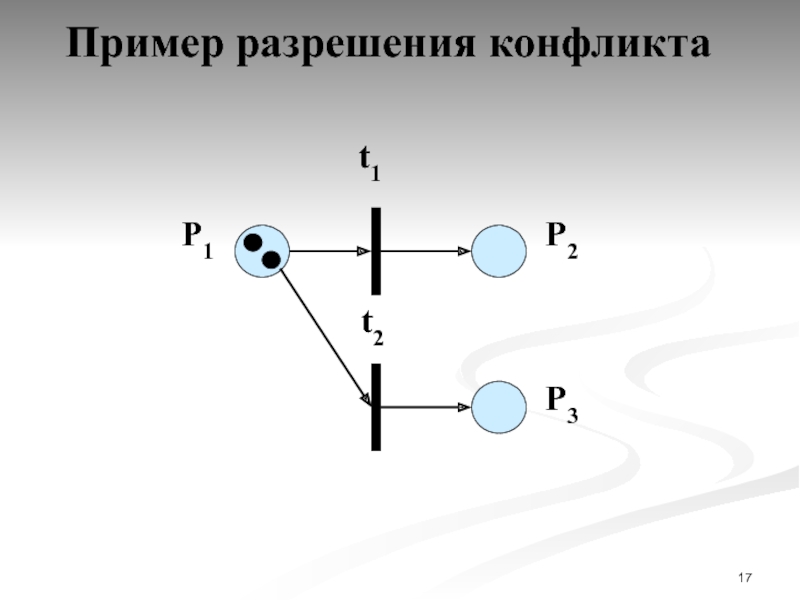
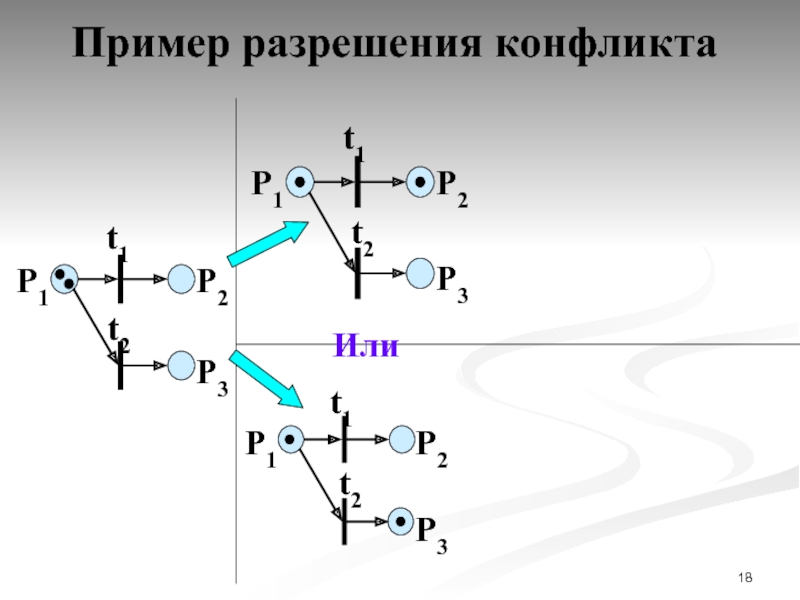
- 17. Пример разрешения конфликта
- 18. Пример разрешения конфликта P1
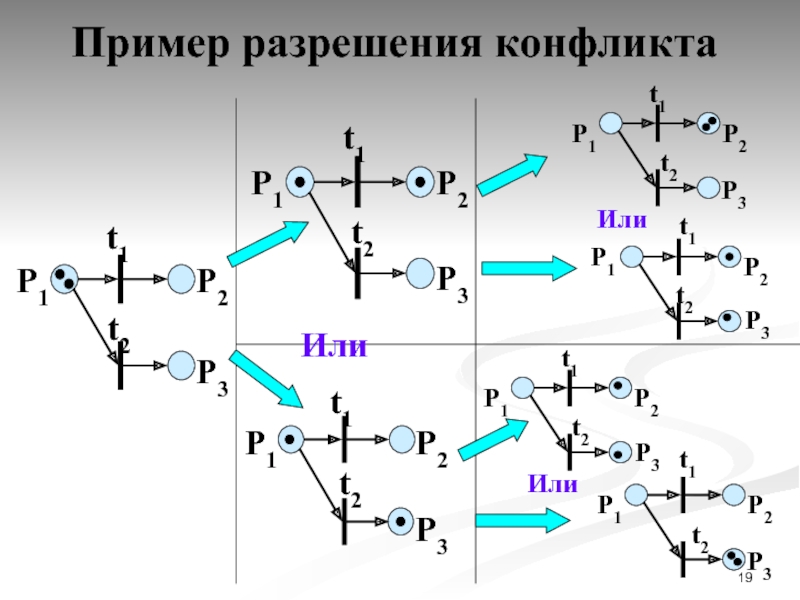
- 19. Пример разрешения конфликта
- 20. Правила срабатывания переходов Правило 4. Параллельная работа.
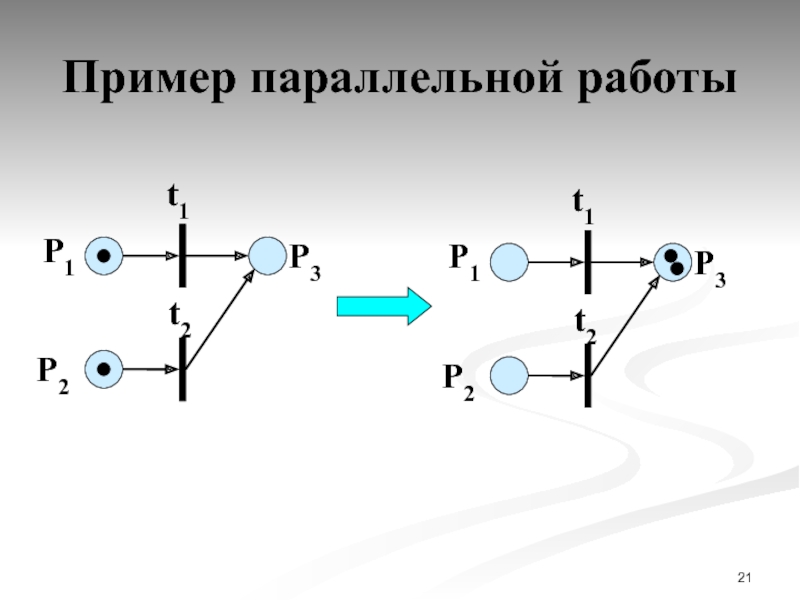
- 21. Пример параллельной работы P1
- 22. P1 P2
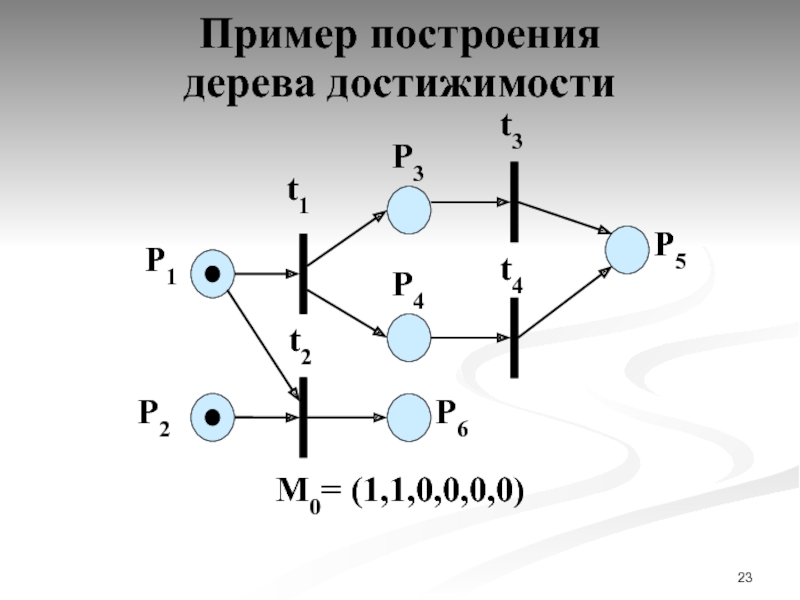
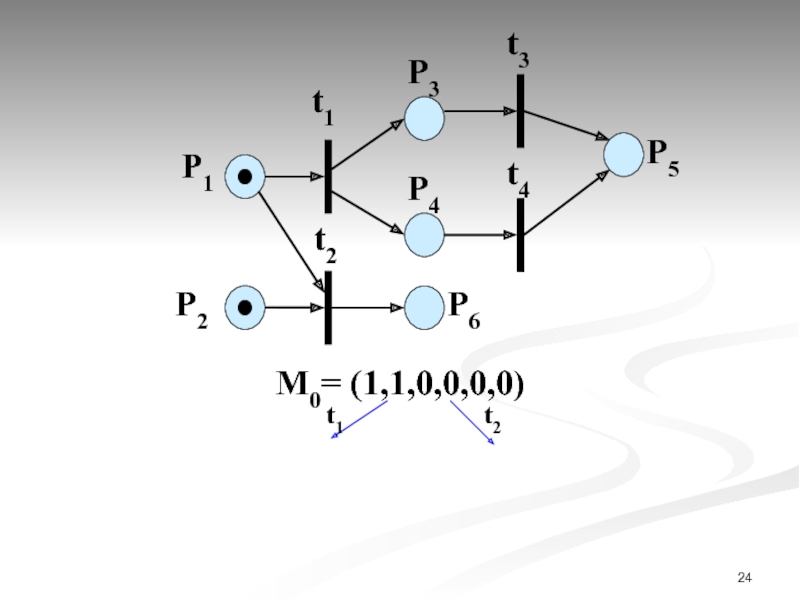
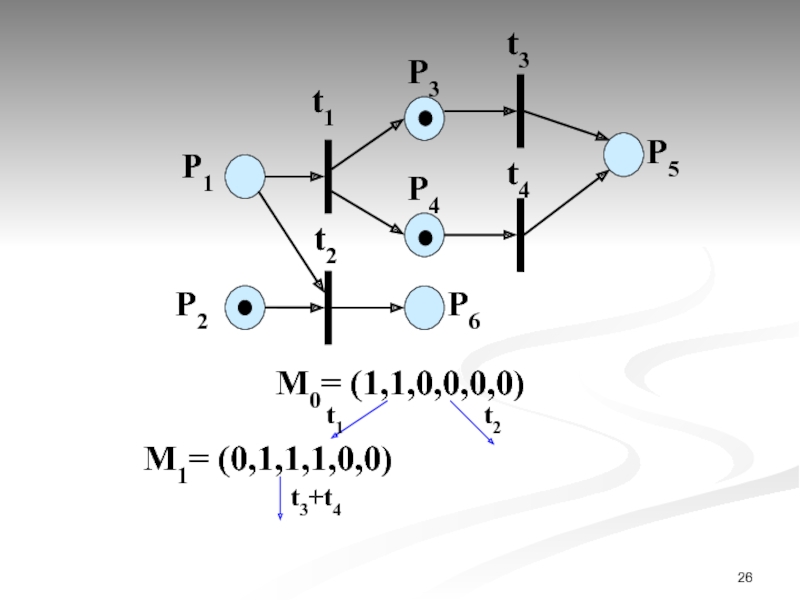
- 23. М0= (1,1,0,0,0,0) Пример построения дерева достижимости
- 24. P1 P2 t1
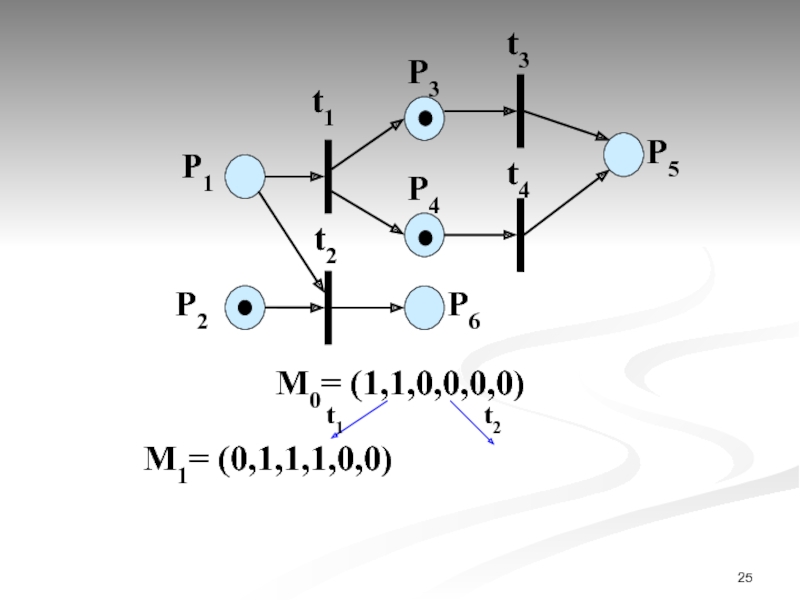
- 25. P1 P2 t1
- 26. P1 P2 t1
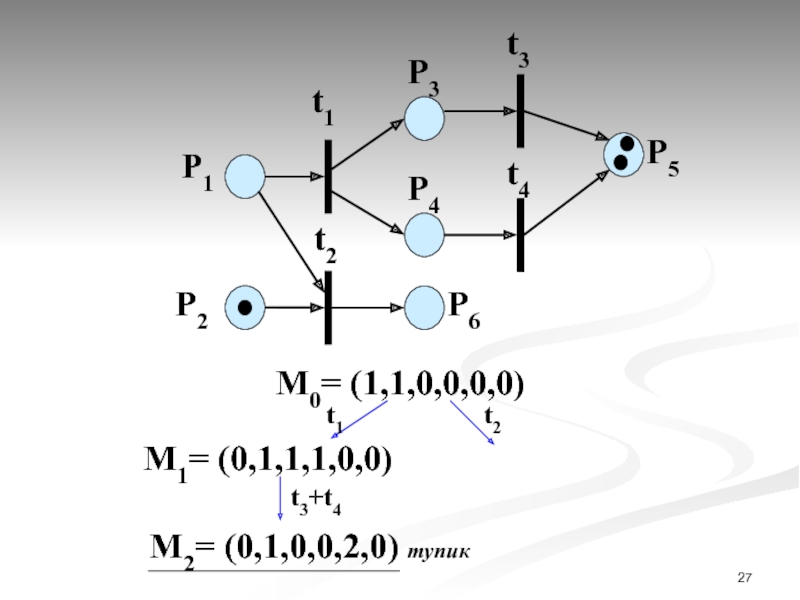
- 27. P1 P2
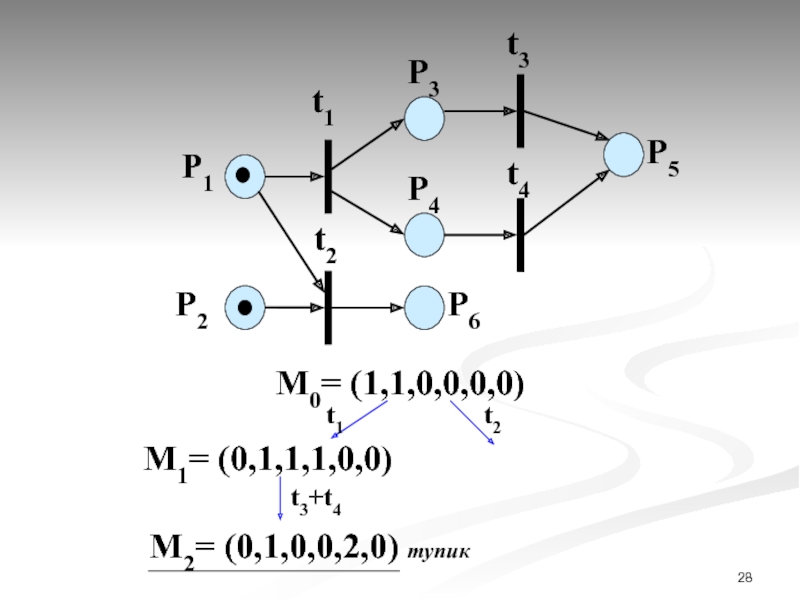
- 28. P1 P2
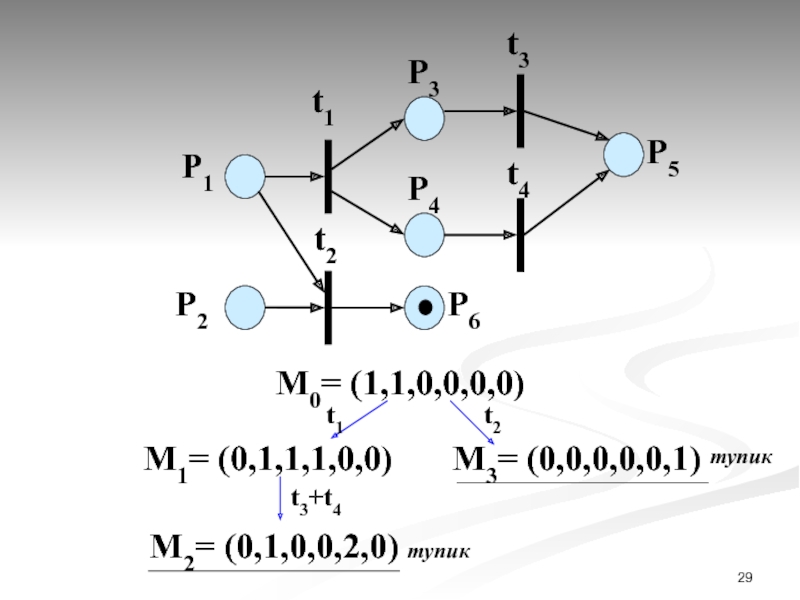
- 29. P1 P2
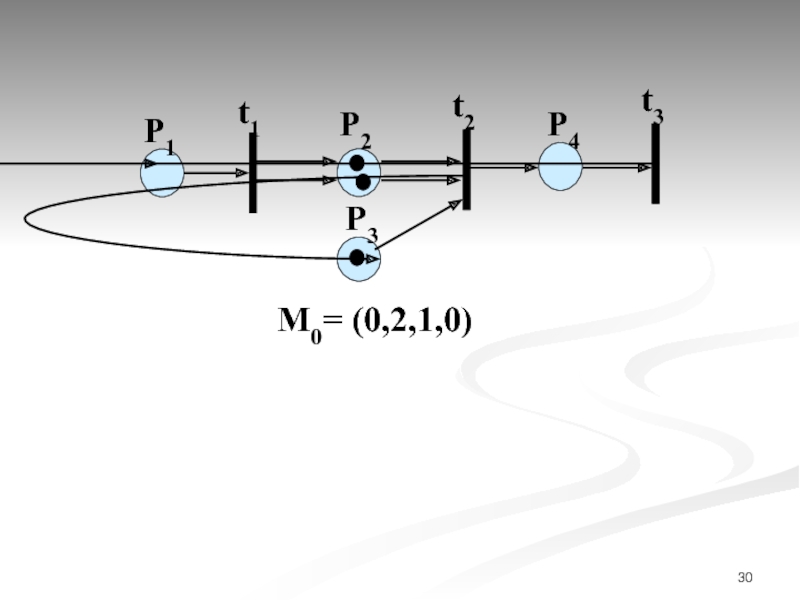
- 30. М0= (0,2,1,0)
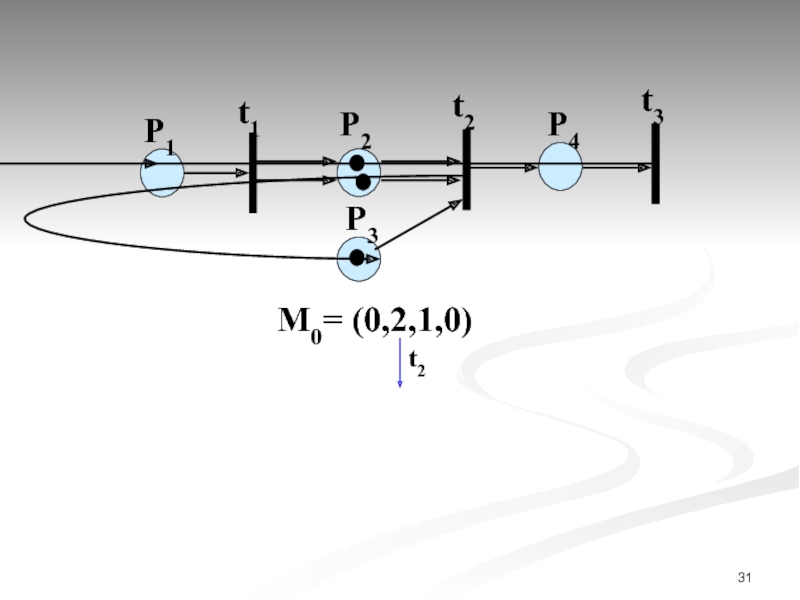
- 31. М0= (0,2,1,0) t2
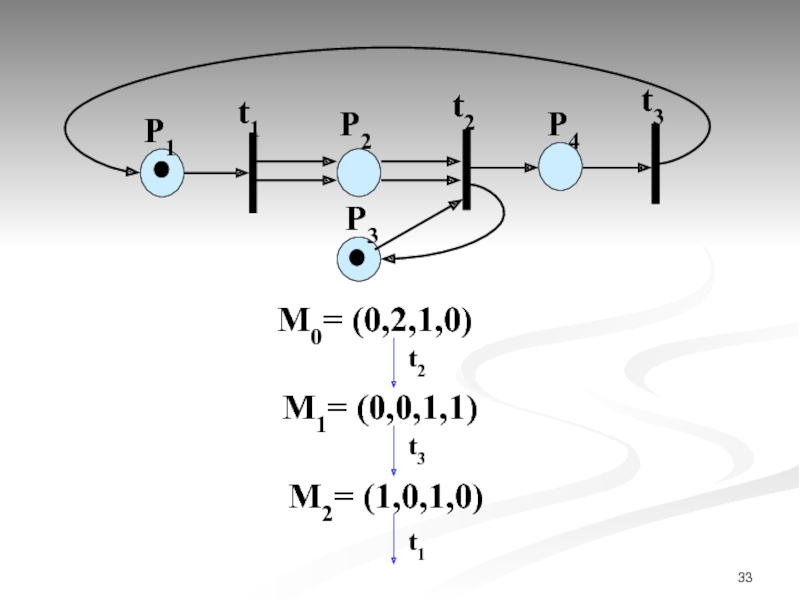
- 32. М0= (0,2,1,0) P1
- 33. М0= (0,2,1,0) P1
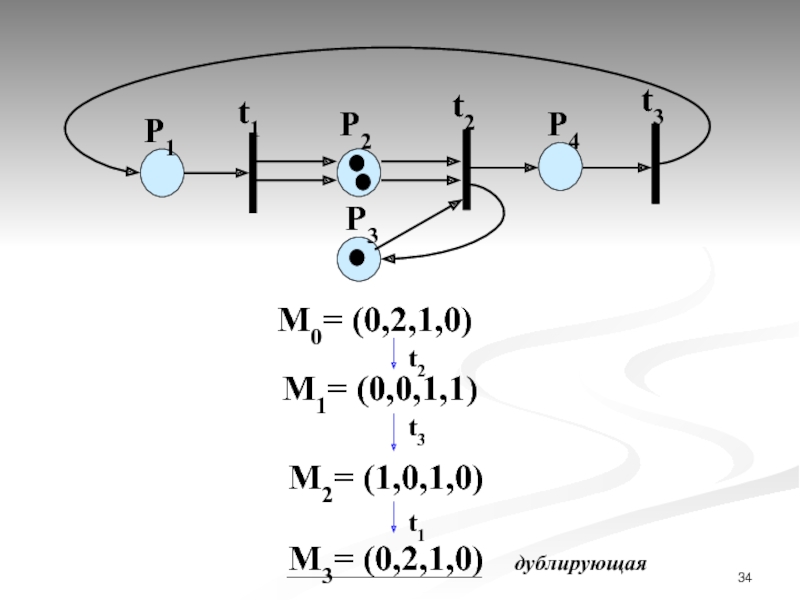
- 34. М0= (0,2,1,0) P1
- 35. P1 P2 t1
Слайд 1ТЕМА 2.
Технологии проектирования информационных систем
Лекция 9.
Применение сетей Петри для моделирования
Слайд 2Методы стадии предпроектного обследования
методы изучения и анализа фактического состояния экономического объекта
методы детального анализа предметной области;
методы формирования нового заданного состояния экономического объекта.
Слайд 3Учет времени при моделировании систем имеет следующие недостатки:
В большой системе приходится
Исчезает информация о причинно-следственных связях между событиями в системе.
События могут происходить внутри неопределенно больших интервалов времени, заранее трудно указать точно время их начала, конца и длительность.
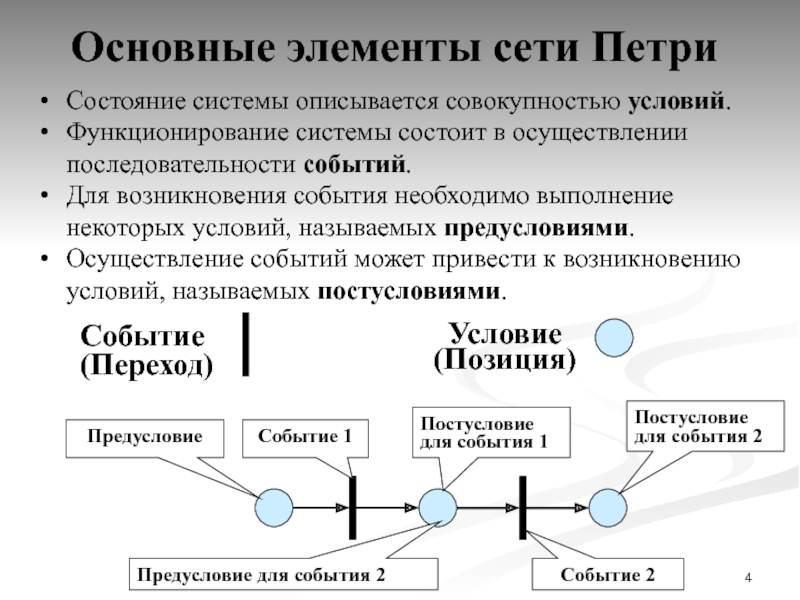
Слайд 4Основные элементы сети Петри
Условие
(Позиция)
Событие
(Переход)
Состояние системы описывается совокупностью условий.
Функционирование системы состоит
Для возникновения события необходимо выполнение некоторых условий, называемых предусловиями.
Осуществление событий может привести к возникновению условий, называемых постусловиями.
Предусловие
Постусловие
для события 1
Событие 1
Событие 2
Постусловие
для события 2
Предусловие для события 2
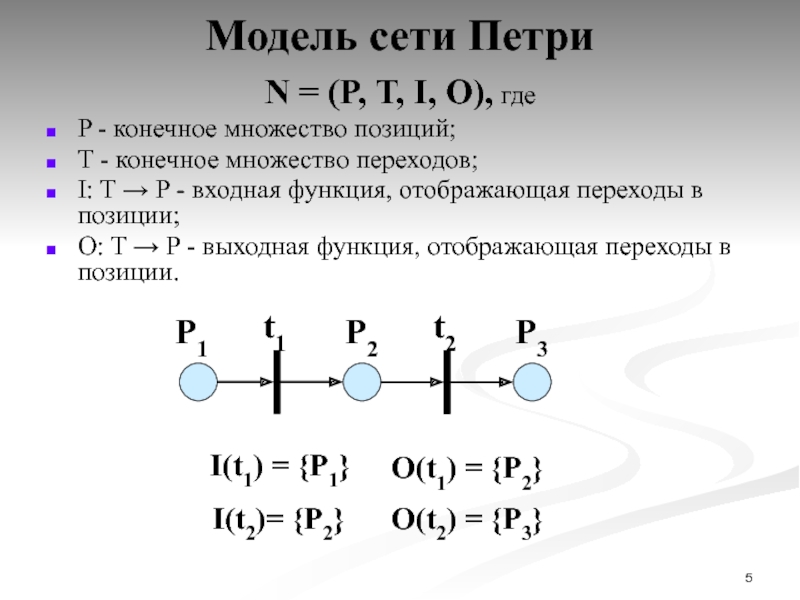
Слайд 5Модель сети Петри
N = (P, T, I, O), где
P -
T - конечное множество переходов;
I: T → P - входная функция, отображающая переходы в позиции;
O: T → P - выходная функция, отображающая переходы в позиции.
t1
t2
P1
P2
P3
I(t1) = {P1}
I(t2)= {P2}
O(t1) = {P2}
O(t2) = {P3}
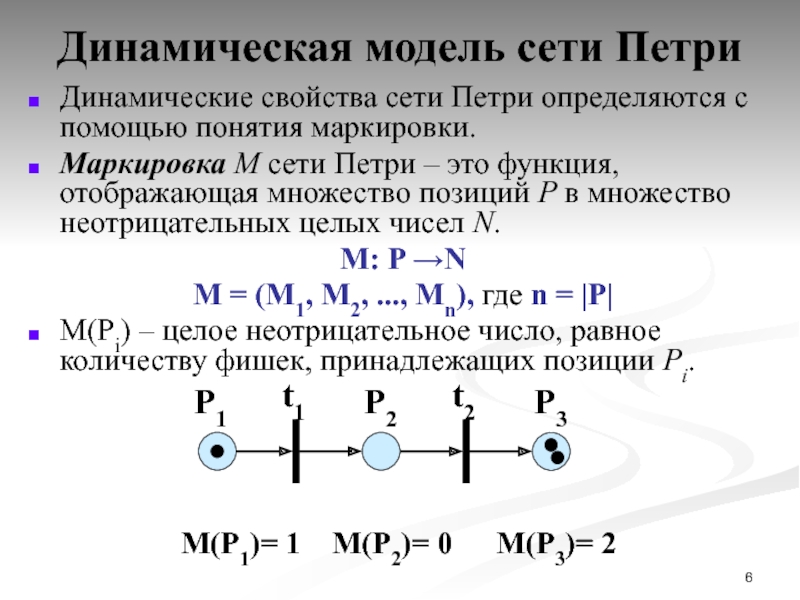
Слайд 6Динамическая модель сети Петри
Динамические свойства сети Петри определяются с помощью понятия
Маркировка M сети Петри – это функция, отображающая множество позиций P в множество неотрицательных целых чисел N.
М: P →N
M = (M1, M2, ..., Mn), где n = |P|
M(Pi) – целое неотрицательное число, равное количеству фишек, принадлежащих позиции Pi.
t1
t2
P1
P2
P3
М(P1)= 1
M(P2)= 0
M(P3)= 2
Слайд 7Свойства сети Петри
Безопасность.
Позиция называется безопасной, если число фишек в ней никогда
Сохраняемость.
В случае, когда фишки интерпретируются как некоторые ресурсы, они не должны ни создаваться, ни уничтожаться. В сети должен действовать закон сохранения. Сеть Петри называется строго сохраняющей, если мощность маркировки постоянна.
Слайд 8Свойства сети Петри
Ограниченность.
Позиция называется К- ограниченной, если число фишек в ней
Достижимость.
Маркировка М’ называется непосредственно достижимой из M, если найдется такой переход tj, разрешенный в M, что при его срабатывании получается маркировка M’. Множество достижимых маркировок сети Петри называется множеством достижимости.
Тупиком в сети Петри называется множество переходов, которые в некоторой достижимой маркировке не разрешены.
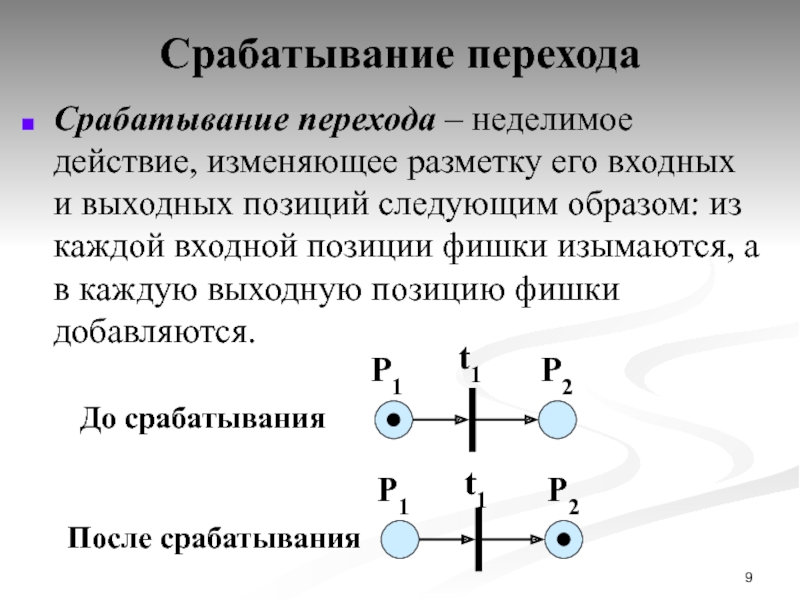
Слайд 9Срабатывание перехода
Срабатывание перехода – неделимое действие, изменяющее разметку его входных и
P1
P2
До срабатывания
t1
P1
P2
После срабатывания
t1
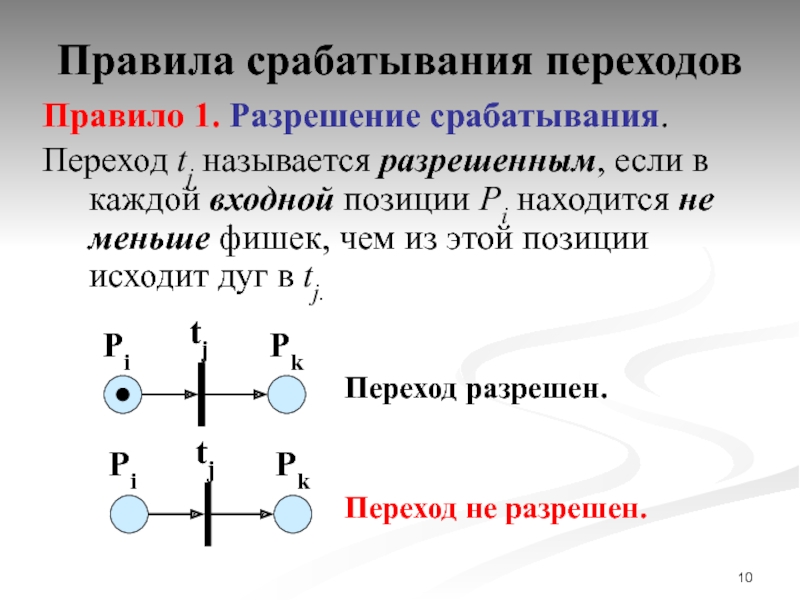
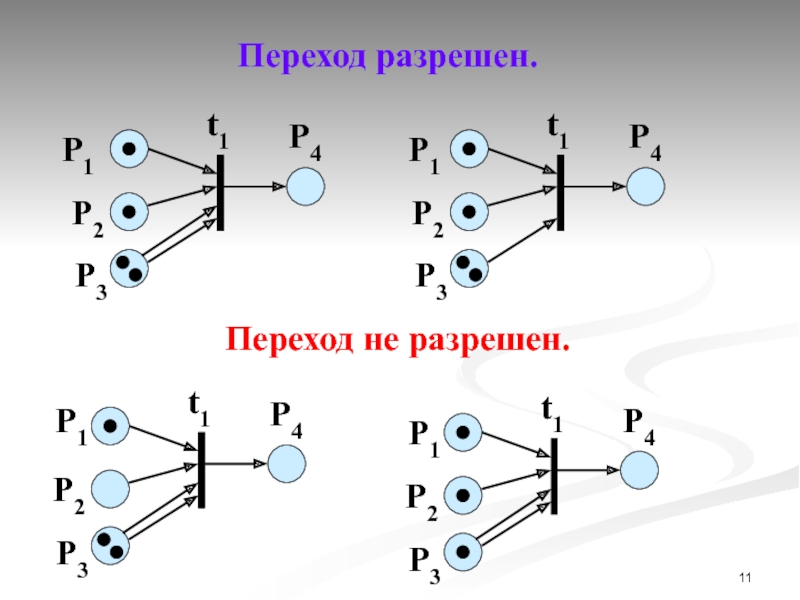
Слайд 10Правила срабатывания переходов
Правило 1. Разрешение срабатывания.
Переход tj называется разрешенным, если
Pi
Pk
tj
Переход разрешен.
Pi
Pk
tj
Переход не разрешен.
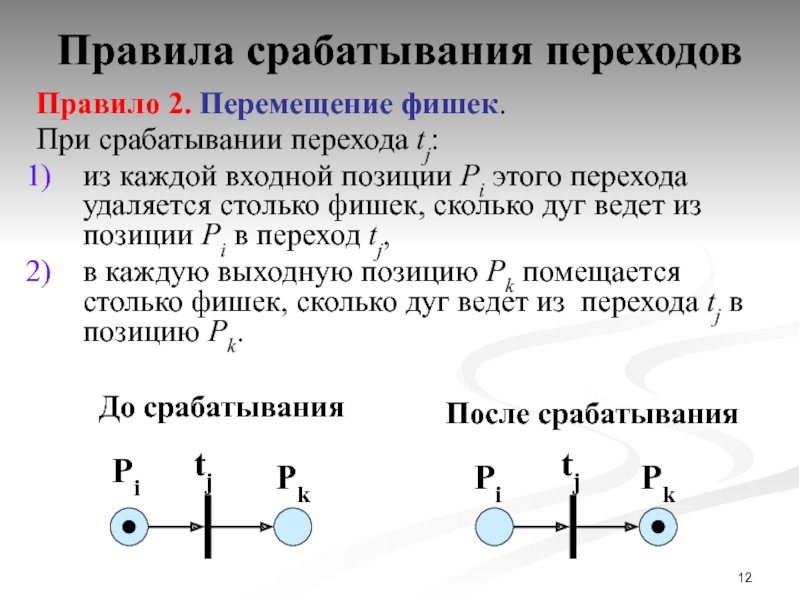
Слайд 12Правила срабатывания переходов
Правило 2. Перемещение фишек.
При срабатывании перехода tj:
из каждой
в каждую выходную позицию Pk помещается столько фишек, сколько дуг ведет из перехода tj в позицию Pk.
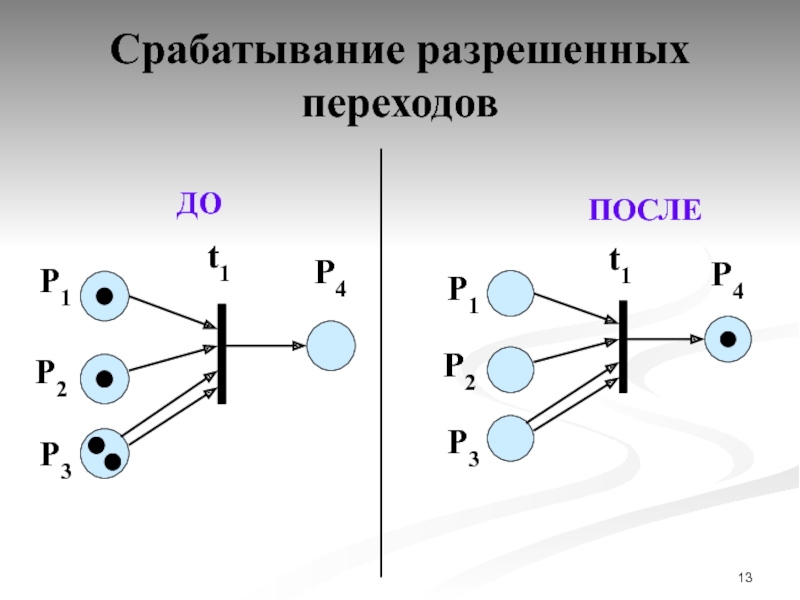
Слайд 15Правила срабатывания переходов
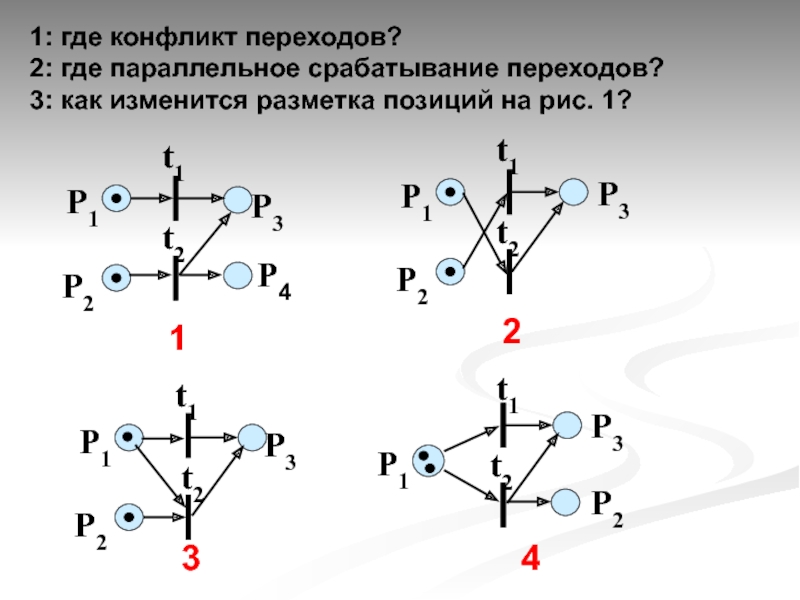
Правило 3. Конфликт.
Если два (и более) перехода могут
Слайд 20Правила срабатывания переходов
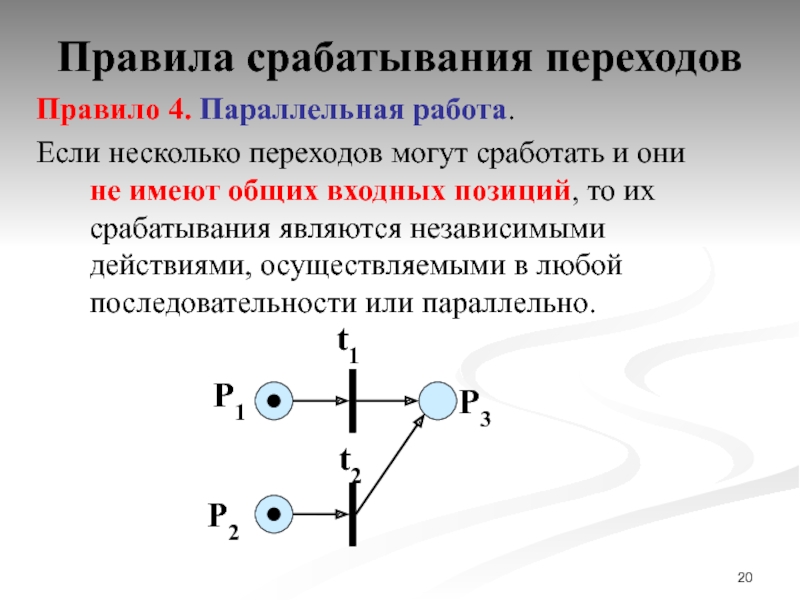
Правило 4. Параллельная работа.
Если несколько переходов могут сработать
P1
P2
t1
P3
t2