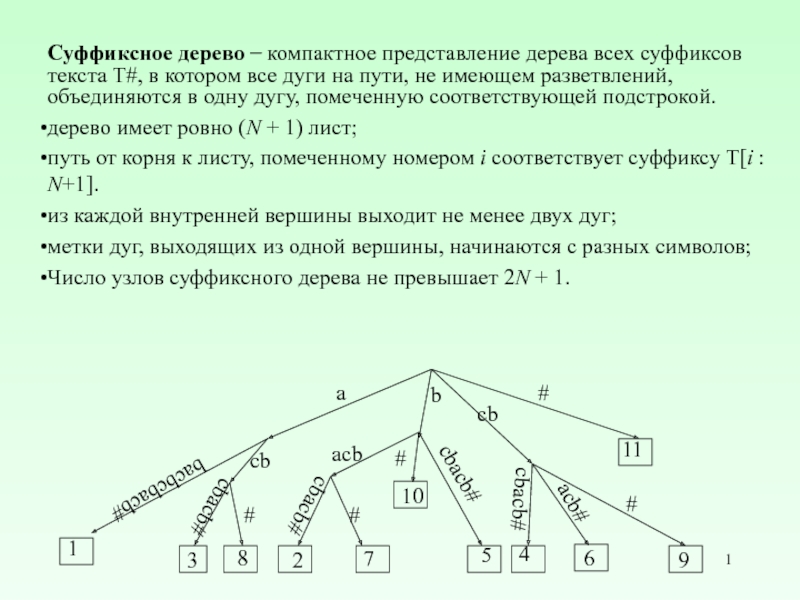
Слайд 1Суффиксное дерево ̶ компактное представление дерева всех суффиксов текста Т#, в
котором все дуги на пути, не имеющем разветвлений, объединяются в одну дугу, помеченную соответствующей подстрокой.
дерево имеет ровно (N + 1) лист;
путь от корня к листу, помеченному номером i соответствует суффиксу T[i : N+1].
из каждой внутренней вершины выходит не менее двух дуг;
метки дуг, выходящих из одной вершины, начинаются с разных символов;
Число узлов суффиксного дерева не превышает 2N + 1.
11
#
cbacb#
6
9
4
1
3
8
2
7
5
10
a
acb
acb#
b
bacbcbacb#
cb
cbacb#
cb
cbacb#
cbacb#
#
#
#
#
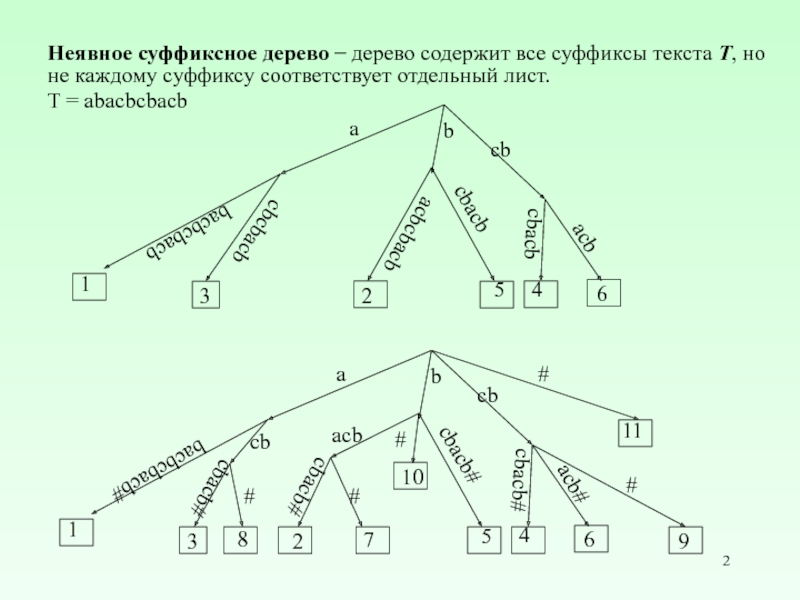
Слайд 2Неявное суффиксное дерево ̶ дерево содержит все суффиксы текста Т, но
не каждому суффиксу соответствует отдельный лист.
T = abacbcbacb
11
#
cbacb#
6
9
4
1
3
8
2
7
5
10
a
acb
acb#
b
bacbcbacb#
cb
cbacb#
cb
cbacb#
cbacb#
#
#
#
#
cbacb
6
4
1
3
2
5
a
acb
b
bacbcbacb
cb
cbacb
cbcbacb
acbcbacb
Слайд 3Построение суффиксных деревьев
Алгоритм Мак-Крейга (McCreight, 1976)
Порядок построения:
T[1 : N+1], T[2 :
N+1], … T[N : N+1], T[N+1 : N+1]
Пример. T = aababbaabbbaaabaa#.
Алгоритм Вайнера (Weiner P., 1973)
Порядок построения:
T[N+1 : N+1], T[N : N+1], … T[2 : N+1], T[1 : N+1]
Алгоритм Укконена (Esko Ukkonen, 1995) строит суффиксное дерево для T [1 : N + 1] через систему неявных деревьев Г1 … Гi … ГN
Гi ̶ неявное суффиксное дерево для T[1 : i], 1 ≤ i ≤ N.
Слайд 4Алгоритм Укконена
Пусть Гi ̶ неявное суффиксное дерево для T[1 : i],
1 ≤ i ≤ N.
Наивный аналог алгоритма Укконена:
Построить дерево Г1.
for i := 1 to N // фаза i + 1
do begin // преобразовать Гi в Г i+1; для этого:
for j := 1 to i +1 // j-й шаг
begin // обеспечить появление пути T[j : i+1]:
для этого найти конец существующего пути T[j : i] и,
если необходимо, продолжить его элементом Ti+1
end
end.
Слайд 5Правила, по которым строится путь T[j : i + 1], в
предположении, что мы находимся в точке, где заканчивается путь T[j : i].
Путь T[j : i] заканчивается в листе. При изменении дерева мы должны к концу метки "листовой" дуги приписать символ Ti+1.
Путь T[j : i] заканчивается во внутренней вершине или на дуге, есть хотя бы одно продолжение этого пути, но не элементом Ti+1.
2а) Путь T[j : i] заканчивается во внутренней вершине w. Добавить лист, помеченный j и дугу (w, j), помеченную символом Ti+1.
2б) Путь T[j : i] заканчивается внутри дуги (u,v). Разбить эту дугу на две: добавить внутреннюю вершину w и дуги (u,w) и (w,v). Конкатенация меток дуг (u,w) и (w,v) составляет метку бывшей дуги (u,v). Метка первой дуги заканчивается суффиксом слова T[j : i]. Далее делать как в 2а.
Путь T[j : i + 1] уже есть в дереве – ничего не надо делать.
Слайд 6Замечания к реализации.
Сжатие дуговых меток. Вместо подстроки, дугу помечаем парой
индексов (k, p), или (j, e), e := i + 1.
К правилу 3. Путь T[j : i + 1] есть в текущем дереве.∃ k | T[j : i + 1] = T[k : p] (k < j, p < i + 1). Тогда T[j + 1: i + 1] = T[k +1 : p]. Путь T[k +1 : p] есть в Гi. То же самое для T[j + 2: i + 1] … Внутренний цикл заканчивается на первом j*, при котором T[j* : i + 1] есть в текущем дереве.
К правилу 1. Если путь T[j' : i] заканчивается в листе, то F(T[j' : i]) = 1. Но тогда F(T[j' – 1 : i]) = 1, и слово T[j' – 1 : i] тоже заканчивается в некотором листе. Это же верно для всех j < j'. Внутренний цикл алгоритма можно начинать не с 1, а с такого j' + 1, что путь T[j': i] заканчивается в листе, а путь T[j'+ 1: i] – во внутренней вершине. Осталось понять, как найти это j'.
К правилу 2 и нахождению j'. Стал листом – листом и останешься. Любое использование правила 2 создает новый лист, причем листья добавляются в порядке возрастания их меток. Пусть в фазе i создан лист j'i (т.е. путь T[j'i : i] теперь заканчивается в листе). В фазе i + 1, при рассмотрении j = j'i мы попадаем в этот самый лист, т.е. используем правило 1. Поэтому начинать внутренний цикл надо с j* – наименьшего j, при котором выполнилось правило 3 на предыдущей (i-й) фазе.

Слайд 7Алгоритм построения суффиксного дерева с учетом замечаний
Построить дерево Г1.
j* :=
1;
for i := 1 to N //фаза i + 1
do begin // преобразовать Гi в Г i+1; для этого:
e := i + 1;
j := j*;
while (в текущем дереве нет пути T[j : i + 1] )
do begin // обеспечить появление пути T[j : i+1]:
для этого найти конец существующего пути T[j : i] и,
если необходимо, продолжить его элементом Ti+1
j := j + 1;
end
if (в текущем дереве есть путь T[j : i + 1]) then j* := j;
end.
Осталось рассмотреть вопрос поиска конца пути T[j : i].
Слайд 8Для поиска конца пути T[j : i] используются суффиксные связи. Они
определяются для внутренних вершин суффиксного дерева.
Пусть aβ – слово, a∈ Σ, β ∈ Σ*; u - вершина, путь из корня к "u" помечен aβ;
v – вершина с путевой меткой β.
Указатель из u в v называется суффиксной связью и обозначается v = suf(u).
Как использовать суффиксные связи (в предположении, что они все существуют и все построены)?
Пусть T[j : i] = a β γ ( a∈ Σ, β ∈ Σ*, γ ∈ Σ*) – последний рассмотренный путь в текущем дереве, (u, j) – дуга, помеченная γ. Следующее действие – поиск в текущем дереве конца строки T[j + 1 : i ] = β γ. Если u – корень, просто спускаемся от корня по β γ. Если u – внутренняя вершина и есть суффиксная связь v = suf(u), то узел v имеет путевой меткой β, а γ должна помечать путь в поддереве v. От листа j идем вверх в узел u, далее по суффиксной связи в v = suf(u), затем от v вниз по пути с меткой γ. Конец пути T[j + 1 : i ] = β γ найден, можно приступать к удлинению этого пути элементом Ti+1.
Слайд 9Осталось показать, что переход по суффиксной связи всегда возможен.
Теорема. Суффиксные
связи определены для всех внутренних вершин суффиксного дерева.
Лемма. Если новая внутренняя вершина w c путевой меткой aβ добавляется к текущему дереву при рассмотрении T[j : i + 1], то либо путь, помеченный β уже заканчивается во внутренней вершине текущего дерева, либо внутренняя вершина, соответствующая строке β будет создана при рассмотрении T[j +1 : i + 1] (т.е. на следующем шаге той же фазы).
Док-во. Новая вершина создается только правилом 2. Это означает, что в дереве есть путь aβc (c ≠ ti+1, aβ = T[j : i + 1]). Тогда в текущем дереве (на (j + 1) шаге (i + 1)-й фазы есть путь βс. Если путь β продолжается не только "с", а еще каким-либо символом, то путь β приводит в вершину u = suf (w). Если путь β продолжается только "с", то на (j + 1)-м шаге (i + 1)-й фазы путь β должен быть продолжен символом ti+1, т.е. вершина u = suf (w) будет создана.
Следствие. В алгоритме Укконена любая вновь созданная вершина будет иметь суффиксную связь с концом следующего продолжения.
Следствие. В любом неявном суффиксном дереве Гi , для любой внутренней вершины w с меткой aβ найдется внутренняя вершина u = suf (w) с путевой меткой β.

Слайд 10Окончательный вариант "действий" во внутреннем цикле алгоритма (построение пути T[j :
i+1]) выглядит следующим образом:
1. От конца пути T[j – 1 : i] идем вверх до первой внутренней вершины v, имеющей исходящую суффиксную связь, либо до корня. Пусть γ – строка между v и концом пути T[j – 1 : i] (возможно, пустая).
2. Если v – корень, пройти от корня по пути T[j : i]. Если v – внутренняя вершина, пройти по суффиксной связи из v в u = suf(v), затем от u вниз по пути с меткой γ. // Конец пути T[j + 1 : i ] = β γ найден, можно приступать к удлинению этого пути элементом Ti+1.
3. Если строки T[j : i + 1] в текущем дереве еще нет, выполняем действия по правилу 2, в частности создаем новую внутреннюю вершину w'.
4. Если в конце пути T[j – 1 : i] была построена новая внутренняя вершина w, устанавливаем суффиксную связь w → w'.
Лемма. Пусть v → u – суффиксная связь, проходимая во время работы алгоритма Укконена. Если вершинная глубина v превосходит вершинную глубину u, то не более чем на единицу.
Теорема. Алгоритм Укконена строит суффиксное дерево для текста длины N за время O(N).
Слайд 12Алгоритм Вайнера (Weiner P., 1973) изначально был предназначен для построения
компактного дерева префикс-идентификаторов, но мы рассмотрим идеи этого алгоритма в приложении к построению суффиксного дерева.
Порядок добавления суффиксов в дерево:
T[N + 1 : N + 1], T[N : N + 1], T[N − 1 : N + 1], … T[2 : N + 1], T[1 : N + 1].
Через Di обозначим суффиксное дерево для T[i : N + 1].
Определение. Для любой позиции i обозначим Head(i)– самый длинный префикс T[i : N + 1], совпадающий с подстрокой T[i +1 : N + 1].
Наивный аналог алгоритма Вайнера тогда выглядит следующий образом:
for i := N downto 1
do begin
найти конец пути с меткой Head(i)в дереве Di+1;
если в конце Head(i) вершины нет, создать ее. Пусть w – эта вершина, старая или новая. Если w создана, расщепить существующую дугу и ее метку так, чтобы w имела путевую метку Head(i). Создать новый лист с номером i и дугу (w,i), помеченную оставшимися символами T[i : N + 1]
end;
Слайд 13Для эффективного поиска Head(i) используются два вектора:
I – индикаторный вектор, L
– вектор связей. Длина векторов = |Σ|.
I, L сопоставляются каждой внутренней вершине и корню.
Пусть u − вершина дерева Di+1 с путевой меткой α; x ∈ Σ.
Iu(x) = 1, если в Di +1 существует путь от корня, помеченный xα, else Iu(x) = 0.
Lu(x) = u', если u' – вершина с путевой меткой xα, else Lu(x) = null.
Переход от Di+1 к построению Di. От листа i + 1, вверх до вершины v, для которой Iv(T[i])= 1. Далее наверх до v' | Lv'(T[i]) = v'' ≠ null. Пусть li – число символов на пути от v к v'. Head(i) заканчивается на дуге, идущей из v'' через li символов.
Как корректировать векторы.
Если алгоритм нашел вершину v с путевой меткой α, для которой Iv(T[i])= 1, то вершина w имеет путевой меткой T[i]α. Lv(T[i]) должно указывать на w.
Если вершина w только создана, все элементы ее вектора связей пустые.
Для каждой вершины u на пути от корня до листа i + 1 должно быть установлено Iu(T[i])= 1. Для вершин выше v это уже выполняется, поэтому менять значение индикаторного вектора нужно по пути от листа i + 1 до v.
Когда новая вершина w создается внутри дуги (v'', z), ее индикаторный вектор нужно скопировать из индикаторного вектора z.
Дуговые метки, как и в алгоритме Укконена, реализуются индексными парами.

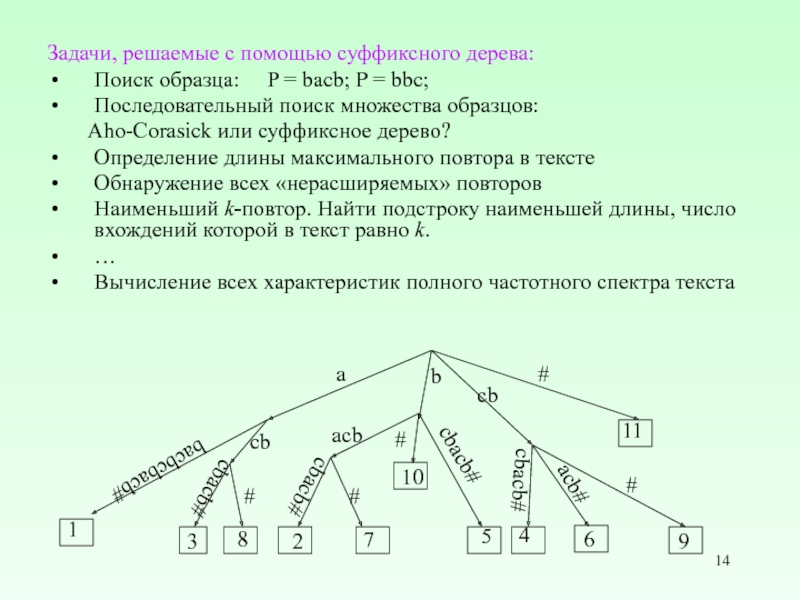
Слайд 14Задачи, решаемые с помощью суффиксного дерева:
Поиск образца: P =
bacb; P = bbc;
Последовательный поиск множества образцов:
Aho-Corasick или суффиксное дерево?
Определение длины максимального повтора в тексте
Обнаружение всех «нерасширяемых» повторов
Наименьший k-повтор. Найти подстроку наименьшей длины, число вхождений которой в текст равно k.
…
Вычисление всех характеристик полного частотного спектра текста
11
#
cbacb#
6
9
4
1
3
8
2
7
5
10
a
acb
acb#
b
bacbcbacb#
cb
cbacb#
cb
cbacb#
cbacb#
#
#
#
#
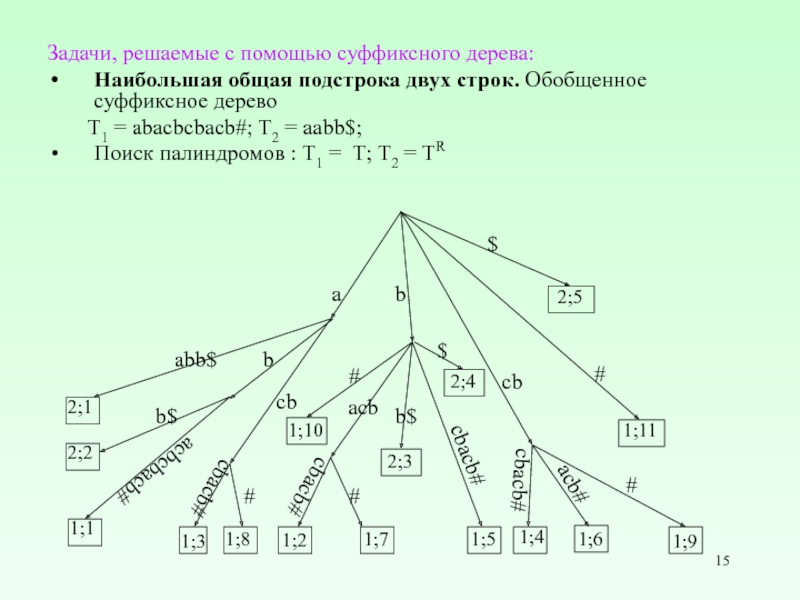
Слайд 15Задачи, решаемые с помощью суффиксного дерева:
Наибольшая общая подстрока двух строк. Обобщенное
суффиксное дерево
T1 = abacbcbacb#; T2 = aabb$;
Поиск палиндромов : T1 = Т; T2 = TR
#
cbacb#
1;6
1;9
1;4
1;3
1;8
1;2
1;7
1;5
a
acb#
acbcbacb#
cb
cbacb#
cb
cbacb#
cbacb#
#
#
#
1;1
acb
b
2;1
2;2
abb$
b$
1;10
#
b
b$
2;4
2;3
1;11
2;5
$
$
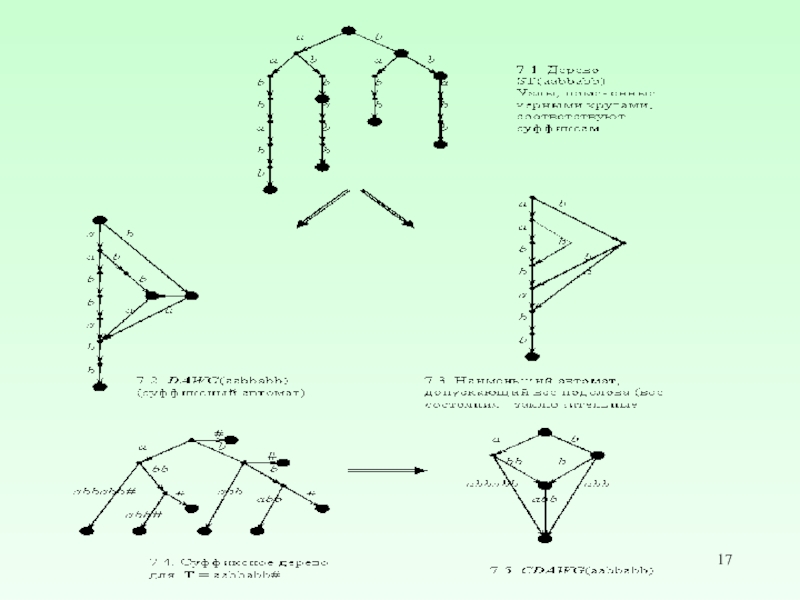
Слайд 16Задачи, решаемые с помощью суффиксного дерева:
Общие подстроки более чем двух строк;
Задача
загрязнения ДНК. Даны строки S1 и S2: S1 − вновь расшифрованная ДНК, S2 − комбинация источников возможного загрязнения. Найти все подстроки S2, которые встречаются в S1 и длина которых не меньше заданного l;
Задача о праймере. Дан набор строк {T1 … TZ} в алфавите Σ. Построить кратчайшую строку S над Σ, которая не встречается как подстрока ни в одном из{T1 … TZ}.
Другой вариант задачи: Задана строка P. Найти подстроки P, не встречающиеся как подстроки в {T1 … TZ}.
Или так: для каждого i вычислить кратчайшую подстроку P, начинающуюся с позиции i и не встречающуюся в качестве подстроки в {T1 … TZ}.
Суффиксно-префиксные совпадения всех пар строк (из заданного множества строк);
Задача о наибольшем общем «продолжении». Найти длину наибольшего общего префикса i-го суффикса строки S1 и j-го суффикса строки S2
Слайд 18Суффиксный массив для строки T[1 : N] есть массив целых чисел
от 1 до N, определяющий лексический порядок всех суффиксов стоки T.
Пример T = mississippi
Pos = (11, 8, 5, 2, 1, 10, 9, 7, 4, 6, 3)
Слайд 19Суффиксный массив для строки T[1 : N] есть массив целых чисел
от 1 до N, определяющий лексический порядок всех суффиксов стоки T.
Пример: T = abacbcbacb. Суффиксный массив – построение путём лексического обхода суффиксного дерева (# < a < b < c)
Pos = (1, 8, 3, 10, 7, 2, 5, 9, 6, 4)
11
#
cbacb#
6
9
4
1
3
8
2
7
5
10
a
acb
acb#
b
bacbcbacb#
cb
cbacb#
cb
cbacb#
cbacb#
#
#
#
#
![Построение суффиксных деревьевАлгоритм Мак-Крейга (McCreight, 1976)Порядок построения:T[1 : N+1], T[2 : N+1], … T[N :](/img/tmb/5/407612/a9a58f81a9e3e2d3416865c76ec6430a-800x.jpg)
![Алгоритм УкконенаПусть Гi ̶ неявное суффиксное дерево для T[1 : i], 1 ≤ i ≤](/img/tmb/5/407612/0857fbbbd9b2a0ea593fcc43f120f01c-800x.jpg)
![Правила, по которым строится путь T[j : i + 1], в предположении, что мы находимся](/img/tmb/5/407612/45b362111ca13947a917d432e9b988fa-800x.jpg)


![Для поиска конца пути T[j : i] используются суффиксные связи. Они определяются для внутренних вершин](/img/tmb/5/407612/90522f54c6bf25e85656afc59bf50cff-800x.jpg)






![Суффиксный массив для строки T[1 : N] есть массив целых чисел от 1 до N,](/img/tmb/5/407612/f4a359c0b2c066e042cb207b0afe4c50-800x.jpg)
![Суффиксный массив для строки T[1 : N] есть массив целых чисел от 1 до N,](/img/tmb/5/407612/86622f100bffa5788cad72116cca8dd6-800x.jpg)