- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Структуры данных презентация
Содержание
- 1. Структуры данных
- 2. При решении конкретной задачи можно
- 3. Очередь (queue) Очередь — абстрактный тип данных
- 4. QUEUE-INIT – инициализирует (создает пустую) очередь;
- 5. Operation QUEUE-INIT Head:=
- 6. Опишем реализацию очереди на
- 7. СТЕК Стек – список, организованный по принципу
- 8. STACK-INIT – инициализирует стек; PUSH
- 9. Стек будем реализовывать также на базе массива
- 10. Operation STACK-INIT Top:= 0;
- 11. Дек (Deque) Дек (deque — double ended
- 12. Базовые операции добавление элемента в начало; добавление
- 13. На практике этот список может быть
- 14. СПИСОК Список – структура, в которой данные
- 15. LIST-INIT – инициализирует список; LIST-FIND
- 17. Опишем реализацию всех операций для двусвязного
- 18. Operation LIST-INIT Head:= NIL; End;
- 19. При добавлении элемента в список можно
- 20. При удалении элемента из списка нужно соединить
- 21. КУЧА Куча - специализированная структура данных типа
- 22. Свойство 1. Высота полного двоичного дерева из
- 23. Функции для работы с кучей а –
- 24. Пирамидальная сортировка О(n * log n)
- 25. Приоритетная очередь Приоритетная очередь — это
- 26. Дома решить задачи из контеста «Занятие 27.09.2016.
Слайд 2
При решении конкретной задачи можно считать, что у нас в
наличии имеется «черный ящик» (его мы и будем называть структурой данных), про который известно, что в нем хранятся данные некоторого рода, и который умеет выполнять некоторые операции над этими данными. Это позволяет отвлечься от деталей и сосредоточиться на характерных особенностях задачи.
Внутри этот «черный ящик» может быть реализован различным образом, при этом следует стремиться к как можно более эффективной (быстрой и экономично расходующей память) реализации.
Внутри этот «черный ящик» может быть реализован различным образом, при этом следует стремиться к как можно более эффективной (быстрой и экономично расходующей память) реализации.
Слайд 3Очередь (queue)
Очередь — абстрактный тип данных с дисциплиной доступа к элементам
«первый пришёл — первый вышел» (FIFO, First In — First Out).
Структуру данных «очередь» (queue), удобно применять в ситуации, когда данные нужно обрабатывать в порядке их получения.
Структуру данных «очередь» (queue), удобно применять в ситуации, когда данные нужно обрабатывать в порядке их получения.
Слайд 4
QUEUE-INIT – инициализирует (создает пустую) очередь;
ENQUEUE (x) – добавляет в
очередь объект x;
DEQUEUE – удаляет из очереди объект, который был добавлен раньше всех, и возвращает в качестве результата удаленный объект (предполагается, что очередь не пуста);
QUEUE-EMPTY – возвращает TRUE, если очередь пуста (не содержит данных), и FALSE – в противном случае.
DEQUEUE – удаляет из очереди объект, который был добавлен раньше всех, и возвращает в качестве результата удаленный объект (предполагается, что очередь не пуста);
QUEUE-EMPTY – возвращает TRUE, если очередь пуста (не содержит данных), и FALSE – в противном случае.
Слайд 5
Operation QUEUE-INIT
Head:= 0;
Tail:= 0;
End;
Operation ENQUEUE (x)
Head:= Head+1;
Q[Head]:= x;
End;
Operation DEQUEUE
Tail:= Tail+1;
Return Q[Tail];
End;
Operation QUEUE-EMPTY
If Tail < Head
Then Return FALSE
Else Return TRUE;
End;
Слайд 6
Опишем реализацию очереди на базе массива. Будем использовать для хранения
данных массив Q[0..N], где число N достаточно велико. При этом данные всегда будут храниться в некотором интервале из последовательных ячеек этого массива. Мы будем использовать переменные Head и Tail для указания границ этого интервала. Более точно, данные хранятся в ячейках с индексами от Tail+1 до Head (предполагается, что Tail < Head; если же Head = Tail, то очередь пуста). Соблюдается также следующее правило: чем позже был добавлен в очередь объект, тем большим будет индекс ячейки массива, в которую он помещается. Это означает, что объект, который был добавлен в очередь раньше всех – это Q[Tail+1].
Все операции над очередью при такой реализации работают за O(1), следовательно, такая реализация эффективна по времени. Однако, число N нужно выбирать достаточно большим (в зависимости от задачи), чтобы избежать «переполнения» очереди, то есть ситуации, когда Head>N. Это может приводить в некоторых задачах к неэффективному использованию памяти.
Все операции над очередью при такой реализации работают за O(1), следовательно, такая реализация эффективна по времени. Однако, число N нужно выбирать достаточно большим (в зависимости от задачи), чтобы избежать «переполнения» очереди, то есть ситуации, когда Head>N. Это может приводить в некоторых задачах к неэффективному использованию памяти.
Слайд 7СТЕК
Стек – список, организованный по принципу LIFO (Last In, First Out
– "последним вошел, первым вышел").
Удобно использовать, когда данные нужно обрабатывать в порядке, обратному порядку получения.
Удобно использовать, когда данные нужно обрабатывать в порядке, обратному порядку получения.
Слайд 8
STACK-INIT – инициализирует стек;
PUSH (x) – добавляет в стек объект
x;
POP – удаляет из стека объект, который был добавлен позже всех, и возвращает в качестве результата удаленный объект (предполагается, что стек не пуст);
STACK-EMPTY – возвращает TRUE, если стек пуст, и FALSE – в противном случае.
POP – удаляет из стека объект, который был добавлен позже всех, и возвращает в качестве результата удаленный объект (предполагается, что стек не пуст);
STACK-EMPTY – возвращает TRUE, если стек пуст, и FALSE – в противном случае.
Слайд 9Стек будем реализовывать также на базе массива S[1..N]. Данные будем хранить
в некотором интервале последовательных ячеек массива (более точно, в ячейках с индексами от 1 до Top). Top – переменная, которая содержит текущее количество объектов в стеке. Как и в случае очереди, соблюдается правило: если i < j Top, то объект S[i] был добавлен в стек раньше, чем объект S[j]. Это гарантирует, что объект S[Top] – тот объект, который был добавлен в стек позже всех.
Слайд 10
Operation STACK-INIT
Top:= 0;
End;
Operation PUSH (x)
Top:= Top+1;
S[Top]:=
x;
End;
Operation POP
Top:= Top-1;
Return S[Top+1];
End;
Operation STACK-EMPTY
If Top > 0
Then Return FALSE
Else Return TRUE;
End;
End;
Operation POP
Top:= Top-1;
Return S[Top+1];
End;
Operation STACK-EMPTY
If Top > 0
Then Return FALSE
Else Return TRUE;
End;
Слайд 11Дек (Deque)
Дек (deque — double ended queue, «двусторонняя очередь») – структура
данных, функционирующая одновременно по двум принцам организации данных: FIFO и LIFO.
Слайд 12Базовые операции
добавление элемента в начало;
добавление элемента в конец;
удаление первого элемента;
удаление последнего
элемента;
чтение первого элемента;
чтение последнего элемента.
чтение первого элемента;
чтение последнего элемента.
Слайд 13
На практике этот список может быть дополнен проверкой дека на пустоту,
получением его размера и некоторыми другими операциями.
В плане реализации двусторонняя очередь очень близка к стеку и обычной очереди: в качестве ее базиса приемлемо использовать как массив, так и список.
В плане реализации двусторонняя очередь очень близка к стеку и обычной очереди: в качестве ее базиса приемлемо использовать как массив, так и список.
Слайд 14СПИСОК
Список – структура, в которой данные выписаны в некотором порядке. В
отличие от массива, этот порядок определяется указателями, связывающими элементы списка в линейную цепочку. Обычно элемент списка представляет собой запись, содержащую ключ (идентификатор) хранящегося объекта, один или несколько указателей и необходимую информацию об объекте. Под ключом подразумевается какая-либо величина, идентифицирующая объект. К примеру, если мы храним информацию о городах, то ключом может быть название города.
Слайд 15
LIST-INIT – инициализирует список;
LIST-FIND (k) – возвращает TRUE, если в
списке есть объект с ключом k, иначе возвращает FALSE;
LIST-INSERT (obj) – добавляет в список объект obj;
LIST-DELETE (x) – удаляет из списка элемент x.
LIST-INSERT (obj) – добавляет в список объект obj;
LIST-DELETE (x) – удаляет из списка элемент x.
Слайд 17
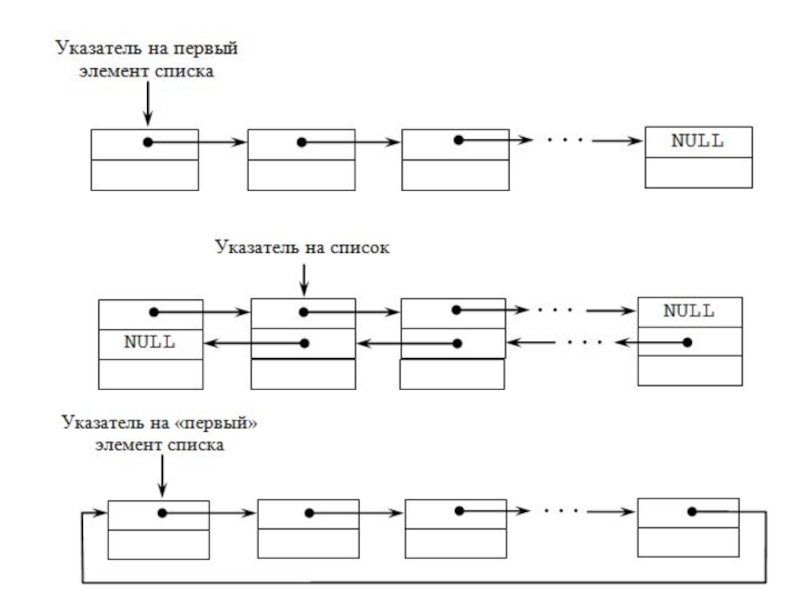
Опишем реализацию всех операций для двусвязного некольцевого списка. Каждый элемент списка
будем хранить как запись, содержащую следующие поля: Key – ключ объекта, Data – дополнительная информация об объекте, Next – указатель на следующий элемент списка (Next = NIL у последнего элемента списка), Prev – указатель на предыдущий элемент списка (Prev = NIL у первого элемета списка). Будем всегда поддерживать указатель Head на первый элемент списка (если список пуст, то Head = NIL). Будем считать, что добавляемые объекты – записи, содержащие поля Key – ключ и Data – дополнительная информация.
Слайд 18Operation LIST-INIT
Head:= NIL;
End;
Operation LIST-FIND (k)
X:= Head;
While X <> NIL Do Begin
If X^.Key = k
Then Return TRUE;
X:= X^.Next;
End;
Return FALSE;
End;
Операция LIST-FIND выполняется за O(n), где n – количество элементов в списке. Это означает, что список не является структурой, эффективно выполняющей поиск.
Слайд 19
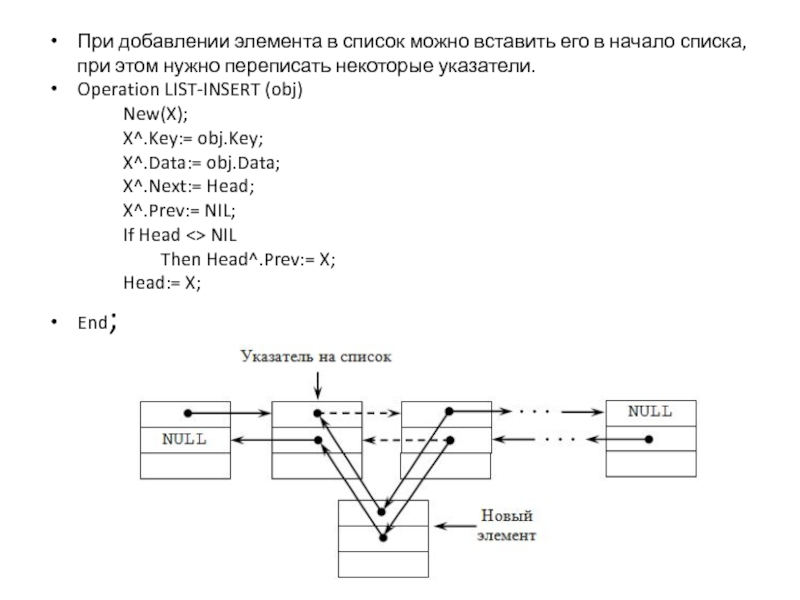
При добавлении элемента в список можно вставить его в начало списка,
при этом нужно переписать некоторые указатели.
Operation LIST-INSERT (obj)
New(X);
X^.Key:= obj.Key;
X^.Data:= obj.Data;
X^.Next:= Head;
X^.Prev:= NIL;
If Head <> NIL
Then Head^.Prev:= X;
Head:= X;
End;
Operation LIST-INSERT (obj)
New(X);
X^.Key:= obj.Key;
X^.Data:= obj.Data;
X^.Next:= Head;
X^.Prev:= NIL;
If Head <> NIL
Then Head^.Prev:= X;
Head:= X;
End;
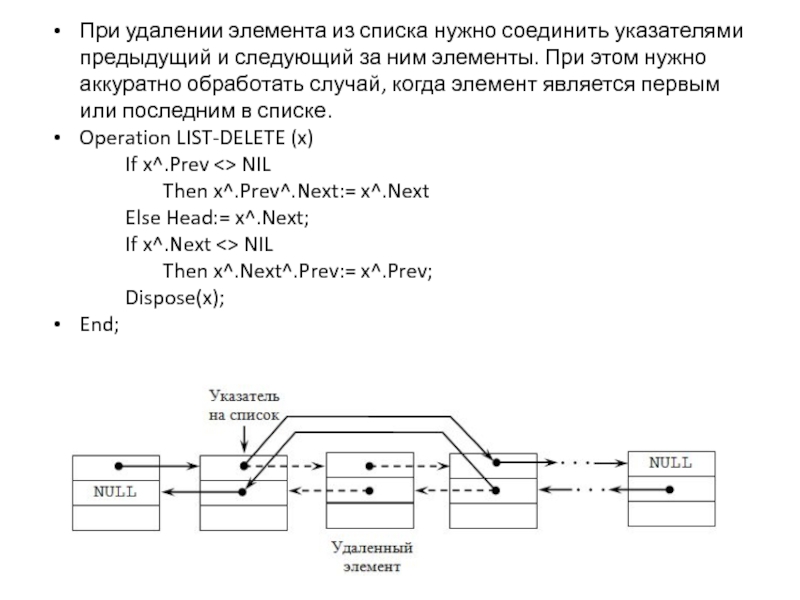
Слайд 20При удалении элемента из списка нужно соединить указателями предыдущий и следующий
за ним элементы. При этом нужно аккуратно обработать случай, когда элемент является первым или последним в списке.
Operation LIST-DELETE (x)
If x^.Prev <> NIL
Then x^.Prev^.Next:= x^.Next
Else Head:= x^.Next;
If x^.Next <> NIL
Then x^.Next^.Prev:= x^.Prev;
Dispose(x);
End;
Operation LIST-DELETE (x)
If x^.Prev <> NIL
Then x^.Prev^.Next:= x^.Next
Else Head:= x^.Next;
If x^.Next <> NIL
Then x^.Next^.Prev:= x^.Prev;
Dispose(x);
End;
Слайд 21КУЧА
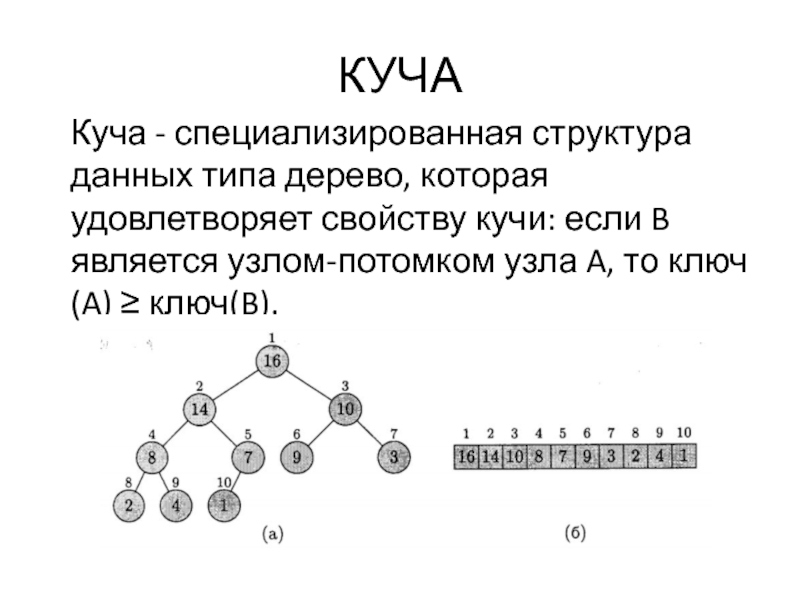
Куча - специализированная структура данных типа дерево, которая удовлетворяет свойству кучи:
если B является узлом-потомком узла A, то ключ(A) ≥ ключ(B).
Слайд 22Свойство 1. Высота полного двоичного дерева из N вершин (то есть
максимальное количество ребер на пути от корня к листьям) есть O(log N).
Свойство 2. Рассмотрим вершину полного двоичного дерева из N вершин, имеющую номер i. Если i = 1, то у вершины i нет отца. Если i > 1, то ее отец имеет номер i div 2. Если 2i < N, то у вершины i есть два сына с номерами 2i и 2i+1. Если 2i = N, то единственный сын вершины i имеет номер 2i. Если 2i > N, то у вершины i нет сыновей.
Свойство 3. В бинарной куче объект H[1] (или объект, хранящийся в корне дерева) имеет минимальное значение ключа из всех объектов.
Свойство 2. Рассмотрим вершину полного двоичного дерева из N вершин, имеющую номер i. Если i = 1, то у вершины i нет отца. Если i > 1, то ее отец имеет номер i div 2. Если 2i < N, то у вершины i есть два сына с номерами 2i и 2i+1. Если 2i = N, то единственный сын вершины i имеет номер 2i. Если 2i > N, то у вершины i нет сыновей.
Свойство 3. В бинарной куче объект H[1] (или объект, хранящийся в корне дерева) имеет минимальное значение ключа из всех объектов.
Слайд 23Функции для работы с кучей
а – это массив, где хранится наша
куча.
size – её текущий размер.
void shiftDown(int i)
{
while (2 * i + 1 < size){
int l = 2 * i + 1;
int r = 2 * i + 2;
int pos = l;
if (r < size && a[pos] > a[r]){
pos = r;
}
if (a[i] < a[pos]) break;
swap(a[i], a[pos]);
i = pos;
}
}
void shiftUp(int i)
{
while (i > 0){
int pos = (i - 1) / 2;
if (a[pos] < a[i]) break;
swap(a[i], a[pos]);
i = pos;
}
}
size – её текущий размер.
void shiftDown(int i)
{
while (2 * i + 1 < size){
int l = 2 * i + 1;
int r = 2 * i + 2;
int pos = l;
if (r < size && a[pos] > a[r]){
pos = r;
}
if (a[i] < a[pos]) break;
swap(a[i], a[pos]);
i = pos;
}
}
void shiftUp(int i)
{
while (i > 0){
int pos = (i - 1) / 2;
if (a[pos] < a[i]) break;
swap(a[i], a[pos]);
i = pos;
}
}
Слайд 24Пирамидальная сортировка О(n * log n)
а – массив, который нужно отсортировать
n
– размер массива а
size – размер кучи
void HeapSort(int n)
{
size = n;
for (int i = 0; i < n / 2; i++)
shiftDown(i);
for (int i = n - 1; i > 0; i--){
size = i;
swap(a[0], a[i]);
shiftDown(0);
}
}
size – размер кучи
void HeapSort(int n)
{
size = n;
for (int i = 0; i < n / 2; i++)
shiftDown(i);
for (int i = n - 1; i > 0; i--){
size = i;
swap(a[0], a[i]);
shiftDown(0);
}
}
Слайд 25Приоритетная очередь
Приоритетная очередь — это абстрактная структура данных на подобии стека
или очереди, где у каждого элемента есть приоритет. Элемент с более высоким приоритетом находится перед элементом с более низким приоритетом. Если у элементов одинаковые приоритеты, они распологаются в зависимости от своей позиции в очереди. Обычно приоритетные очереди реализуются с помощью кучи.
Методы такие же, как и у обычной очереди. Ниже приведена реализация некоторых из них
void push(Type x){
a[size] = x;
shiftUp(size);
size++;
}
Type pop(){
Type res = a[0];
size--;
swap(a[0], a[size]);
shiftDown(0);
return res;
}
Методы такие же, как и у обычной очереди. Ниже приведена реализация некоторых из них
void push(Type x){
a[size] = x;
shiftUp(size);
size++;
}
Type pop(){
Type res = a[0];
size--;
swap(a[0], a[size]);
shiftDown(0);
return res;
}
Слайд 26Дома решить задачи из контеста «Занятие 27.09.2016. Структуры данных» в группе
на codeforces.com
Темы задач:
А – стек
В – стек
С – очередь
D – очередь
Е – список
F – приоритетная очередь
G – работа с кучей
H – очередь
На основе решения домашних заданий будет составляться рейтинг.
Удачи.
Темы задач:
А – стек
В – стек
С – очередь
D – очередь
Е – список
F – приоритетная очередь
G – работа с кучей
H – очередь
На основе решения домашних заданий будет составляться рейтинг.
Удачи.




![Operation QUEUE-INIT Head:= 0; Tail:= 0; End; Operation ENQUEUE (x) Head:= Head+1; Q[Head]:= x;](/img/tmb/3/283666/d4a8f1ebb9ec618720840d4c0f2add50-800x.jpg)
![Опишем реализацию очереди на базе массива. Будем использовать для хранения данных массив Q[0..N], где](/img/tmb/3/283666/c804da1e5c843600d83464fe9587dbb1-800x.jpg)


![Стек будем реализовывать также на базе массива S[1..N]. Данные будем хранить в некотором интервале последовательных](/img/tmb/3/283666/e1ed840ed755f0ee665e08dc5b6729a0-800x.jpg)
![Operation STACK-INIT Top:= 0; End; Operation PUSH (x) Top:= Top+1; S[Top]:= x; End; Operation POP](/img/tmb/3/283666/800ab742f838f4852e855e7e7c82b4d6-800x.jpg)