Разработала: старший преподаватель Андреева Н.В.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления. Перевод чисел из одной системы счисления в другую систему счисления презентация
Содержание
- 1. Системы счисления. Перевод чисел из одной системы счисления в другую систему счисления
- 2. Системы счисления – это совокупность приёмов и
- 3. Число q, равное количеству различных цифр в
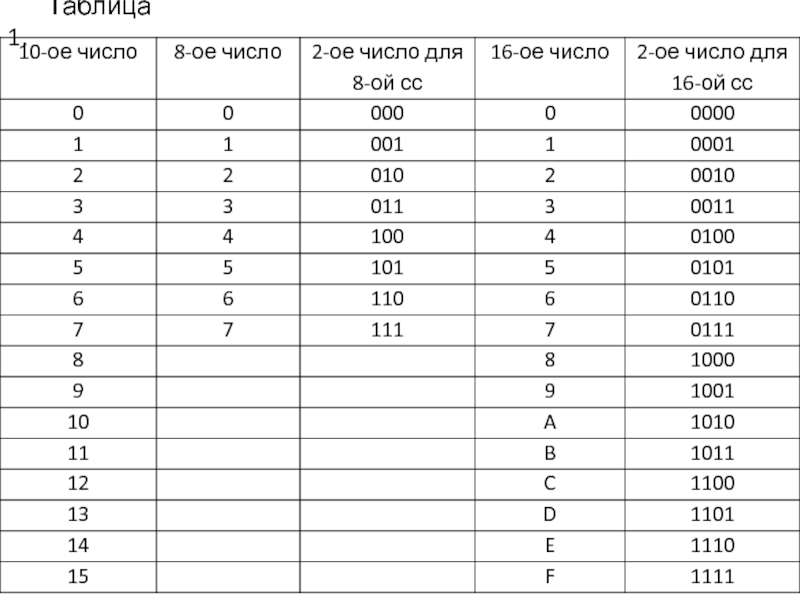
- 4. Таблица 1.
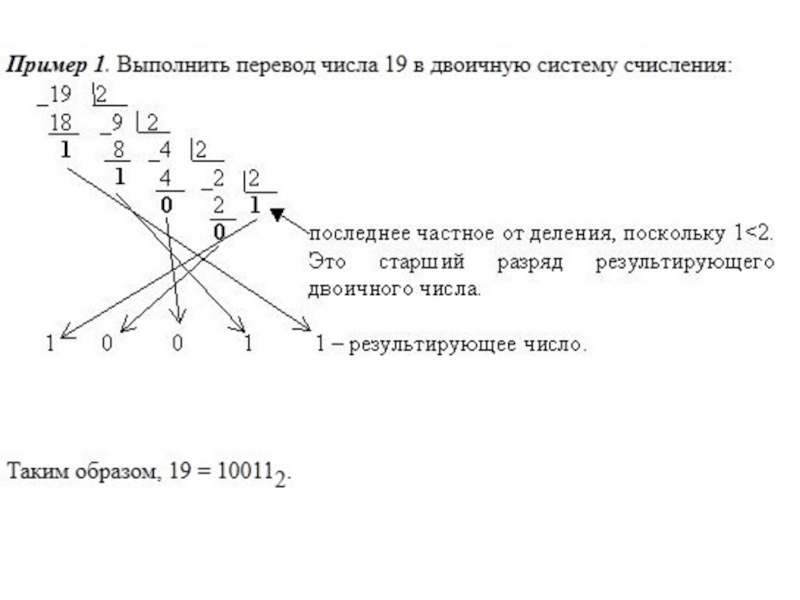
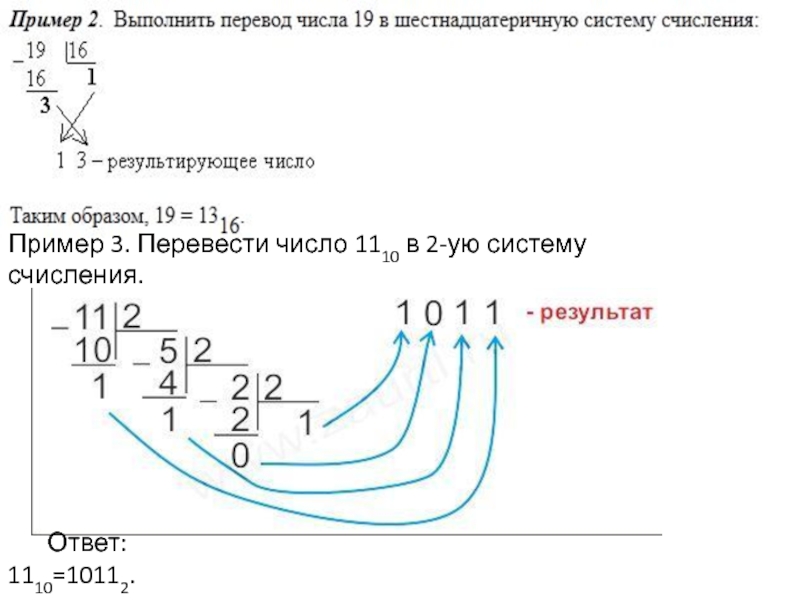
- 6. Пример 3. Перевести число 1110 в 2-ую систему счисления. Ответ: 1110=10112.
- 7. Пример 4. Перевести число 12210 в 8-ую
- 8. Пример 4. Выполнить перевод числа 101101 в
- 9. Пример 7. Выполнить перевод числа 101101 из
Системы счисления – это совокупность приёмов и правил для записи чисел цифровыми знаками, символами. Все системы счисления делятся на две большие группы:
Слайд 1Лекция «Системы счисления. Перевод чисел из одной системы счисления в другую
систему счисления»
Слайд 2Системы счисления – это совокупность приёмов и правил для записи чисел
цифровыми знаками, символами.
Все системы счисления делятся на две большие группы:
Слайд 3Число q, равное количеству различных цифр в алфавите позиционной системы счисления,
называется основанием системы счисления.
Число Nq в позиционной системе счисления с основанием q и алфавитом А в многочленной записи выглядит следующим образом:
Nq=anan-1...а1aoa-1a-2...a-m=anqn +an-1qn-1 +…+a1q1+ a0q0+ … +а-1q-1+a-2q-2+ ...+a-mqm,
где an , an-1,..., a1, аo, a-1, a-2,..., a-m - цифры из алфавита А; п. п - 1,..., 1, 0, -1,-2, ...,-т - номера разрядов.
Число Nq в позиционной системе счисления с основанием q и алфавитом А в многочленной записи выглядит следующим образом:
Nq=anan-1...а1aoa-1a-2...a-m=anqn +an-1qn-1 +…+a1q1+ a0q0+ … +а-1q-1+a-2q-2+ ...+a-mqm,
где an , an-1,..., a1, аo, a-1, a-2,..., a-m - цифры из алфавита А; п. п - 1,..., 1, 0, -1,-2, ...,-т - номера разрядов.
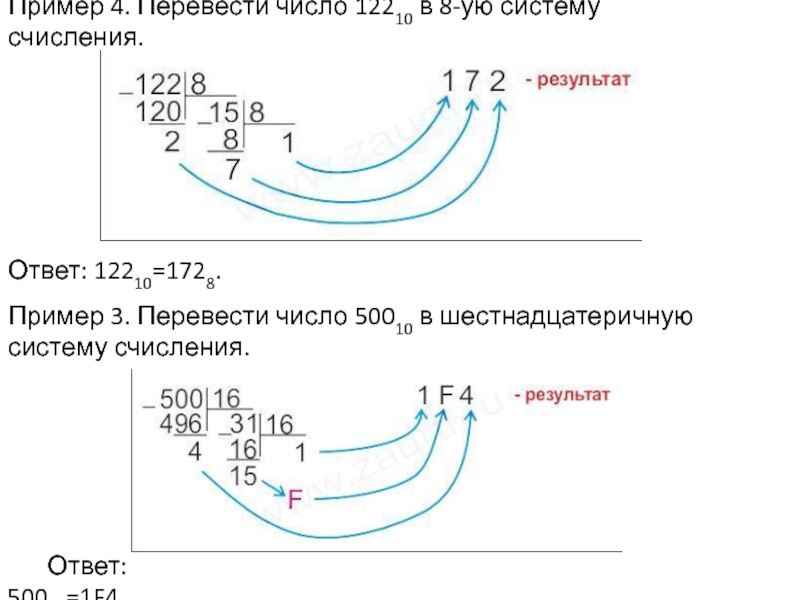
Слайд 7Пример 4. Перевести число 12210 в 8-ую систему счисления.
Пример 3. Перевести
число 50010 в шестнадцатеричную систему счисления.
Ответ: 50010=1F416.
Ответ: 12210=1728.
Слайд 8Пример 4. Выполнить перевод числа 101101 в десятичную систему счисления из
двоичной.
1504131201102 = 1*25 + 0 * 24 + 1 * 23 +1 * 22 + 0 * 21 +1 * 20 = 32+0+8+4+0+1= 4510
Пример 5. Выполнить перевод числа 1DC из шестнадцатеричной системы счисления в десятичную систему счисления.
12D1C016 = 1 * 162 + 13 * 161 +12 * 160 = 256+208+12 = 47616
Пример 6. Выполнить перевод числа 2312 из восьмеричной системы счисления в десятичную систему счисления.
233211208 = 2 * 83 +3 * 82 +1 * 81 +2 * 80 = 1024+192+8+2=122610
1504131201102 = 1*25 + 0 * 24 + 1 * 23 +1 * 22 + 0 * 21 +1 * 20 = 32+0+8+4+0+1= 4510
Пример 5. Выполнить перевод числа 1DC из шестнадцатеричной системы счисления в десятичную систему счисления.
12D1C016 = 1 * 162 + 13 * 161 +12 * 160 = 256+208+12 = 47616
Пример 6. Выполнить перевод числа 2312 из восьмеричной системы счисления в десятичную систему счисления.
233211208 = 2 * 83 +3 * 82 +1 * 81 +2 * 80 = 1024+192+8+2=122610
Слайд 9Пример 7. Выполнить перевод числа 101101 из двоичной систему счисления в
восьмеричную: разобьем исходную запись числа на триады двоичных разрядов:
101101 ? 101 101 1012 ? 58; 1012 ? 58
Итак, 1011012 = 558.
Пример 8. Выполнить перевод числа 101101 из двоичной системы счисления в шестнадцатеричную: разобьем исходную запись числа на тетрады двоичных разрядов:
101101 ? 0010 1101 00102 ? 216; 11012 ? d16
Итак, 1011012 = 2d16
Пример 9. Выполнить перевод числа 2312 из восьмеричной системы счисления в двоичную: каждой цифре в записи числа поставим в соответствие триаду двоичных цифр:
28 ? 0102; 38 ? 0112; 18 ? 0012; 28 ? 0102.
Итак, 23128 = 100110010102
Пример 10. Выполнить перевод числа 1DC из шестнадцатеричной системы счисления в двоичную: каждой цифре в записи числа поставим в соответствие тетраду двоичных цифр:
116 ? 00012; D16 ? 11012; C16 ? 11002
Итак, 1dc16 = 1110111002
101101 ? 101 101 1012 ? 58; 1012 ? 58
Итак, 1011012 = 558.
Пример 8. Выполнить перевод числа 101101 из двоичной системы счисления в шестнадцатеричную: разобьем исходную запись числа на тетрады двоичных разрядов:
101101 ? 0010 1101 00102 ? 216; 11012 ? d16
Итак, 1011012 = 2d16
Пример 9. Выполнить перевод числа 2312 из восьмеричной системы счисления в двоичную: каждой цифре в записи числа поставим в соответствие триаду двоичных цифр:
28 ? 0102; 38 ? 0112; 18 ? 0012; 28 ? 0102.
Итак, 23128 = 100110010102
Пример 10. Выполнить перевод числа 1DC из шестнадцатеричной системы счисления в двоичную: каждой цифре в записи числа поставим в соответствие тетраду двоичных цифр:
116 ? 00012; D16 ? 11012; C16 ? 11002
Итак, 1dc16 = 1110111002
