- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления. Методическое пособие презентация
Содержание
- 1. Системы счисления. Методическое пособие
- 2. Понятие системы счисления
- 3. Цифра Цифра — это условный знак для
- 4. Два вида систем счисления Существуют
- 5. Непозиционные системы счисления В непозиционных
- 6. Позиционные системы счисления В позиционных
- 7. Запись числа как суммы произведений
- 8. Расстановка позиций цифр в числе 757,7210
- 9. Любая
- 10. Основание определяет Название системы счисления Количество цифр в этой системе счисления
- 11. Двоичная система счисления
- 12. Двоичная система счисления Электрический сигнал,
- 13. Правило перевода чисел из любой позиционной системы
- 14. Пример перевода из двоичной системы счисления в
- 15. Восьмеричная система счисления
- 16. Пример перевода из восьмеричной системы счисления в
- 17. Шестнадцатеричная система счисления
- 18. Пример перевода из шестнадцатеричной системы счисления в
- 19. Правило перевода чисел из десятичной системы счисления
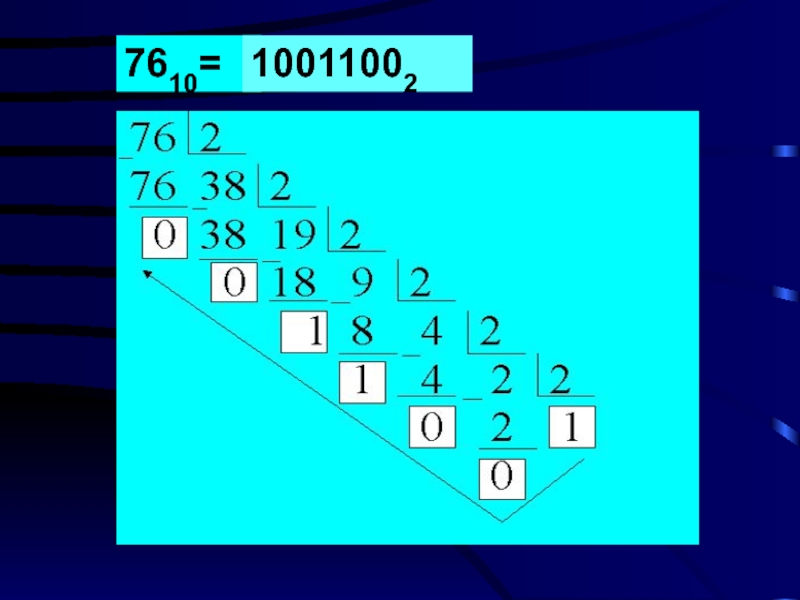
- 20. 7610= 10011002
- 21. 0,37510= 0,0112
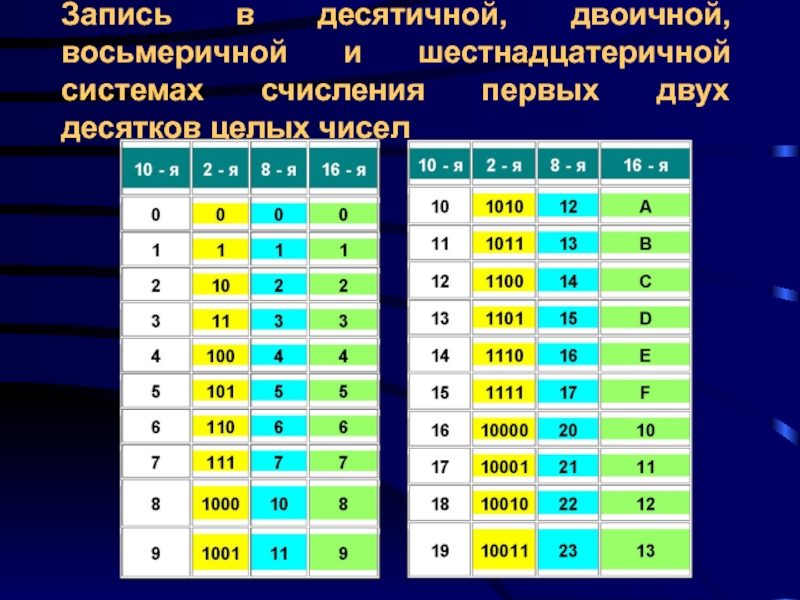
- 22. Запись в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления первых двух десятков целых чисел
- 23. Родственные системы Двоичная, основание 2 = 21
- 24. Запись двоичных чисел вне ЭВМ очень громоздкая.
- 25. Примеры перевода из двоичной системы
- 26. Перевод из восьмеричной системы счисления в двоичную
- 27. Примеры перевода из двоичной системы счисления в
- 28. Перевод из шестнадцатеричной системы в
Понятие системы счисления Система счисления — это способ записи чисел с помощью заданного набора специальных знаков.
Слайд 2Понятие системы счисления
Система счисления — это способ записи чисел
с помощью заданного набора специальных знаков.
Слайд 3Цифра
Цифра — это условный знак для записи чисел.
Пример: в десятичной системе счисления 10 цифр
0 1 2 3 4 5 6 7 8 9
С помощью этих цифр записываются десятичные числа.
0 1 2 3 4 5 6 7 8 9
С помощью этих цифр записываются десятичные числа.
Слайд 5Непозиционные системы счисления
В непозиционных системах вес цифры (т.е. тот
вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.
Пример: В римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
Пример: В римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
Слайд 6Позиционные системы счисления
В позиционных системах счисления вес каждой цифры
изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Пример: В десятичном числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Пример: В десятичном числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Слайд 7Запись числа как суммы произведений
Запись числа 757,710
означает сокращенную запись выражения
700 + 50 + 7 + 0,7 =
=7•102 + 5•101 + 7•100 + 7•10-1 =
=757,710
700 + 50 + 7 + 0,7 =
=7•102 + 5•101 + 7•100 + 7•10-1 =
=757,710
Слайд 12Двоичная система счисления
Электрический сигнал, передающий информацию в ПК, может
иметь один из двух уровней напряжения: низкий (кодируется нулем) и высокий (кодируется единицей). Обработка двоичного кода происходит по законам двоичной системы счисления.
Слайд 13Правило перевода чисел из любой позиционной системы счисления в десятичную
Переводимое число необходимо записать в виде суммы произведений цифр числа на основание системы счисления в степени, соответствующей позиции цифры в числе.
Слайд 14Пример перевода из двоичной системы счисления в десятичную
5 4 3
2 1 0 -1 -2
111000.112=1•25+1•24+1•23+1•2-1+1•2-2 =
= 32 + 16 + 8 + ½ + ¼ =
= 56,7510
111000.112=1•25+1•24+1•23+1•2-1+1•2-2 =
= 32 + 16 + 8 + ½ + ¼ =
= 56,7510
Слайд 16Пример перевода из восьмеричной системы счисления в десятичную
2 1 0 -1
421.58 = 4•82+2•81+1•80+5•8-1 =
= 256 + 16 + 1 + 5/8 =
= 273,62510
421.58 = 4•82+2•81+1•80+5•8-1 =
= 256 + 16 + 1 + 5/8 =
= 273,62510
Слайд 18Пример перевода из шестнадцатеричной системы счисления в десятичную
1 0 -1
A7.C16 = 10•161+7•160+12•16-1 =
= 160 + 7 + 12/16 =
= 167,7510
A7.C16 = 10•161+7•160+12•16-1 =
= 160 + 7 + 12/16 =
= 167,7510
Слайд 19Правило перевода чисел из десятичной системы счисления в двоичную
Перевод целой
части
сводится к записи в обратном порядке
остатков от деления исходного числа и
каждого последующего частного на 2.
сводится к записи в обратном порядке
остатков от деления исходного числа и
каждого последующего частного на 2.
Дробная часть получается из целых частей (0 или 1) при ее последовательном умножении на 2 до тех пор, пока дробная часть не обратится в 0 или получится требуемое количество знаков после разделительной точки.
Слайд 22Запись в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления первых двух
десятков целых чисел
Слайд 23Родственные системы
Двоичная, основание 2 = 21
Восьмеричная, основание 8 = 23
Шестнадцатеричная,
основание 16 = 24
Слайд 24Запись двоичных чисел вне ЭВМ очень громоздкая. Для сокращенной записи двоичных
чисел используют 8-ричную и 16-ричную системы счисления.
При переводе из двоичной в восьмеричную систему каждые три двоичные цифры заменяются соответствующей восьмеричной цифрой.
При переводе из двоичной в шестнадцатеричную каждые четыре двоичные цифры заменяются одной шестнадцатеричной цифрой.
При переводе из двоичной в восьмеричную систему каждые три двоичные цифры заменяются соответствующей восьмеричной цифрой.
При переводе из двоичной в шестнадцатеричную каждые четыре двоичные цифры заменяются одной шестнадцатеричной цифрой.
Родственные системы
Слайд 25
Примеры перевода из двоичной системы счисления в восьмеричную
100110111.0012=
100
110
111.
0012
100110111.0012=
4
7.
6
18
10100101110.112=
1102
101
010
6.
110.
100
10100101110.112=
5
2
4
68
Слайд 26Перевод из восьмеричной системы счисления в двоичную
Такой перевод осуществляется путем подстановки:
каждая 8-ричная цифра заменяется на соответствующие ей три двоичных.
74.68=
310.58=
111
011
1102
000.
100.
001
1012
Слайд 27Примеры перевода из двоичной системы счисления в шестнадцатеричную
100110111.0012=
100110111.0012=
10100101110.112=
10100101110.112=
0111.
0101
1110.
1
0001
7.
0011
11002
0010
216
00102
3
2
С16
Е.
5
Слайд 28
Перевод из шестнадцатеричной системы в двоичную
Такой перевод осуществляется путем обратной
подстановки: каждая 16-ричная цифра заменяется на соответствующие ей четыре двоичных.
C1B.316=
1011.
1100
0001
00112
AF0.116=
0000.
1010
1111
00012
