- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сходство и различие радиотехнических САУ и других автоматических систем презентация
Содержание
- 1. Сходство и различие радиотехнических САУ и других автоматических систем
- 2. Предмет и задачи курса Предмет изучения дисциплины
- 3. Сходство и различие радиотехнических САУ и других
- 4. Краткая история развития систем автоматического управления Первые
- 5. Тема 1: «Общая характеристика систем автоматического
- 6. Основные понятия и определения Автоматика –
- 7. Функциональная схема замкнутой автоматической системы
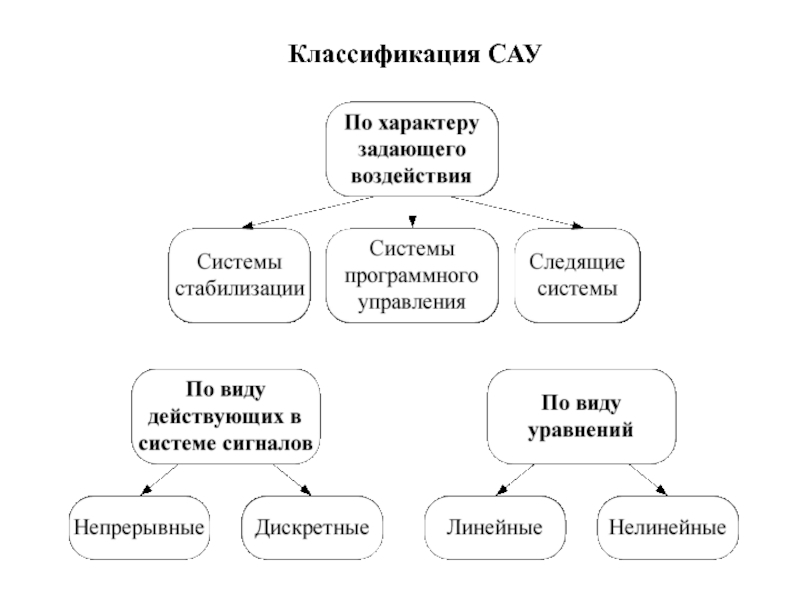
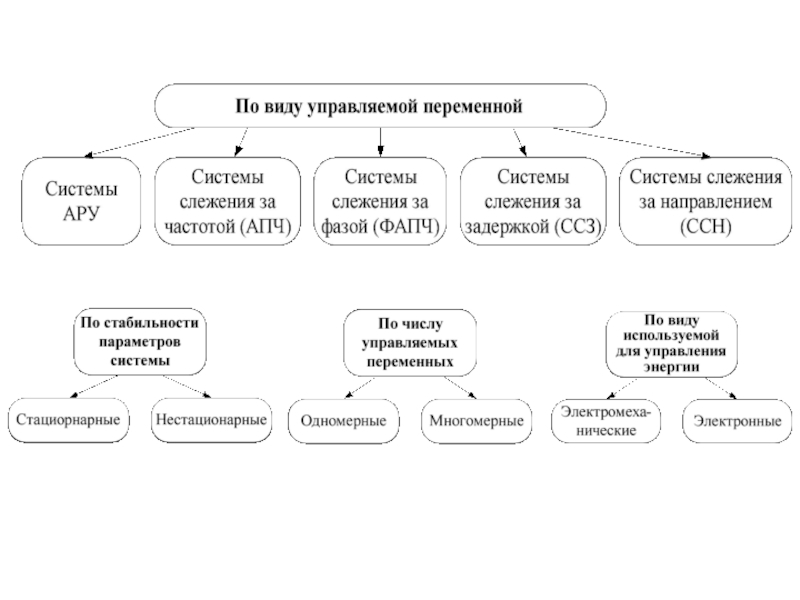
- 8. Классификация САУ
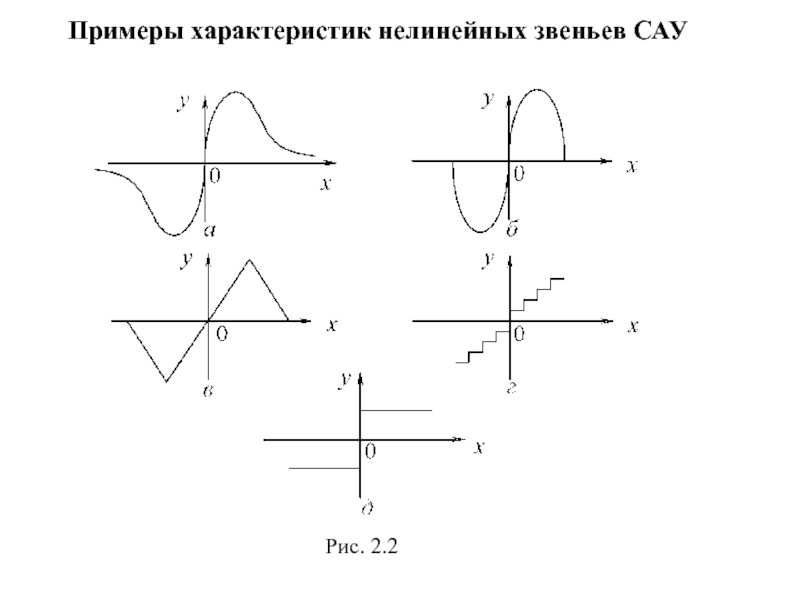
- 10. Примеры характеристик нелинейных звеньев САУ Рис. 2.2
- 11. Статическая характеристика – алгебраическое уравнение y=ƒ(x) (для
- 12. Литература В.Н. Бондаренко Основы автоматики : учеб.
- 13. Тема 2: «Типовые звенья систем автоматического
- 14. Интегрирующее звено Уравнение динамики интегрирующего звена ,
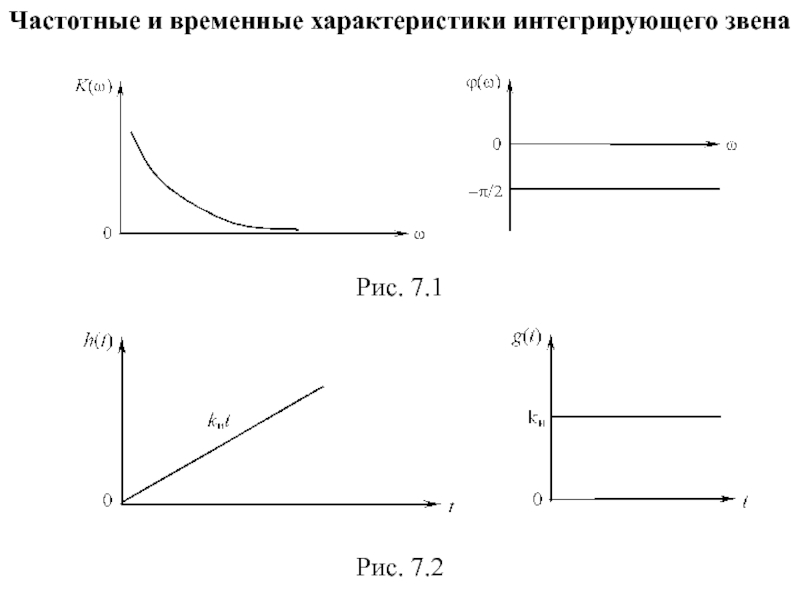
- 15. Частотные и временные характеристики интегрирующего звена Рис. 7.1 Рис. 7.2
- 16. Форсирующее звено где k – коэффициент
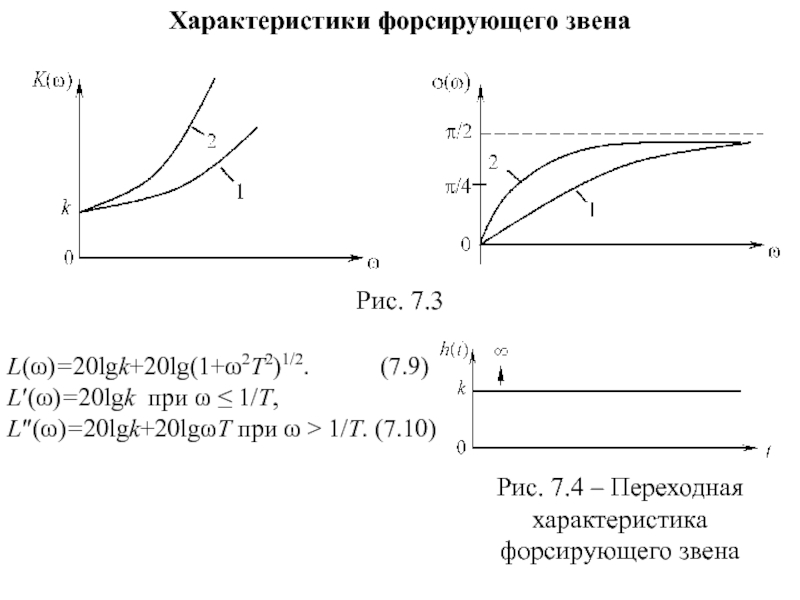
- 17. Характеристики форсирующего звена Рис. 7.3 L(ω)=20lgk+20lg(1+ω2T2)1/2.
- 18. Способы реализации форсирующего звена
- 19. Колебательное звено Уравнение динамики где Т –
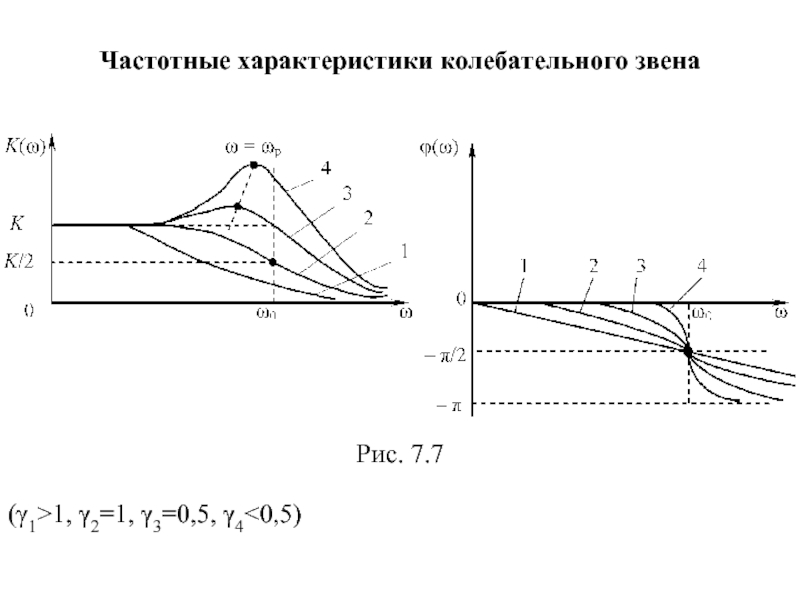
- 20. Частотные характеристики колебательного звена Рис. 7.7 (γ1>1, γ2=1, γ3=0,5, γ4
- 21. Резонансная частота При γ ≥
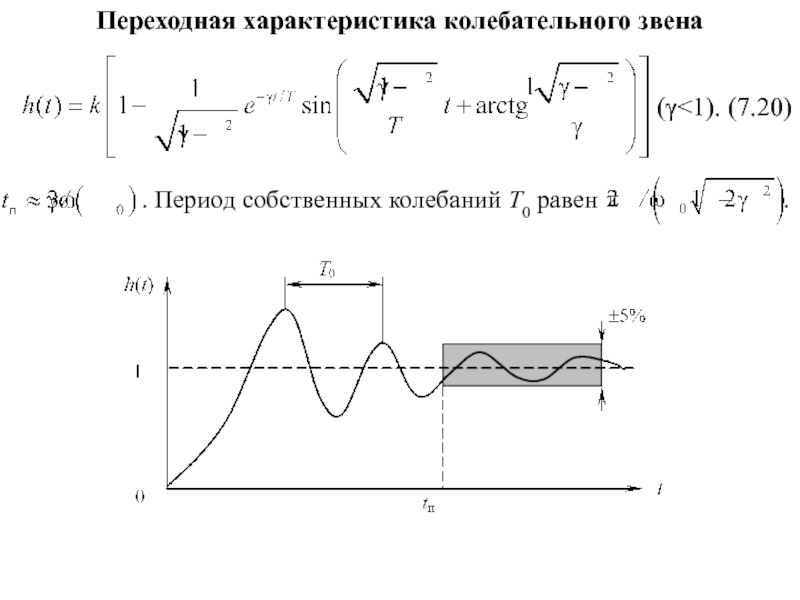
- 22. Переходная характеристика колебательного звена
- 23. Тема 8: «Передаточные функции систем радиоавтоматики»
- 24. Обобщенная функциональная схема САУ U0(t, y) –
- 25. Обобщенная структурная схема САУ e = x
- 26. Дискриминационная характеристика Зависимость крутизны ДХ от соотношения
- 27. Флуктуационная характеристика Флуктуационная характеристика (ФХ) –
- 28. Дифференциальное уравнение системы y(t) = K(p)[U(e)+
- 29. Правила преобразования структурных схем Последовательное соединение звеньев Рис. 4.6
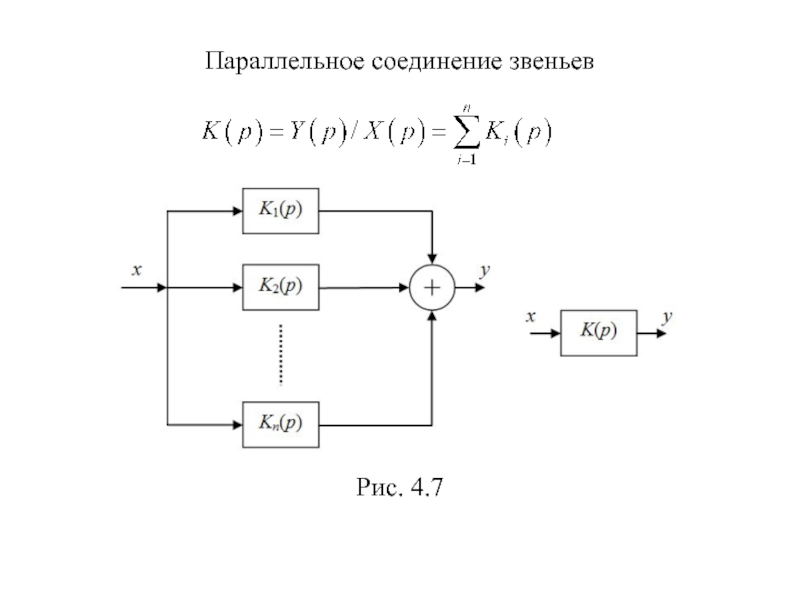
- 30. Параллельное соединение звеньев Рис. 4.7
- 31. Передаточные функции замкнутой системы Передаточная функция замкнутой
- 32. САУ как фильтр Рис. 5.2 Kз(jω) –
- 33. САУ – фильтр нижних частот по отношению
- 34. Тема 9: «Устойчивость автоматических систем»
- 35. Общие требования к устойчивости систем Характеристическое
- 36. Рис. 6.1
- 37. Составляющие свободного движения где Сi – постоянные
- 38. Алгебраические критерии устойчивости Критерий Гурвица: главный определитель,
- 39. Частотные критерии устойчивости Критерий Найквиста:
- 40. Рис. 6.3
- 41. Рис. 6.4
- 42. Запас устойчивости Запас по фазе Δϕ –
- 43. Запретные области по заданным запасам ΔK и
- 44. Тема 10: «Оценка качества автоматических систем
- 45. Типовые воздействия в виде детерминированных функций времени:
- 46. Рис. 7.1 tп – время
- 47. Переходный процесс: монотонный (кривая 1), апериодический (кривая
- 48. Цифровое моделирование непрерывных САУ Разностное уравнение
- 49. Анализ качества переходного процесса по АЧХ
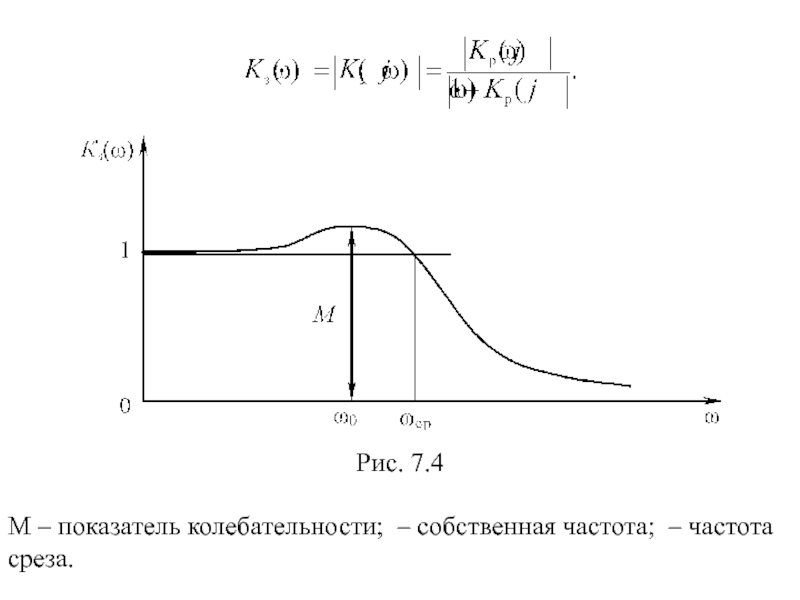
- 50. Рис. 7.4 M – показатель колебательности; – собственная частота; – частота среза.
- 51. Рис. 7.5 Кривая 1 − АЧХ
- 52. Оценка качества переходного процесса по ЛАХ разомкнутой
- 53. ЛАХ типовых систем Рис. 7.7
- 54. Тема 11: «Точность автоматических систем при
- 55. Точность САУ при типовых воздействиях Точность
- 56. Статические ошибки Статическая ошибка – ошибка
- 57. Динамические ошибки Динамическая ошибка eд(t) –
- 58. Установившееся значение ошибки Для статических систем
- 59. Установившееся значение ошибки i = 1
- 60. Для астатической системы второго порядка скоростная ошибка
- 61. Откуда C2/2=1/K2, так как C0=C1=0.
- 62. Тема 12: «Точность автоматических систем при воздействии
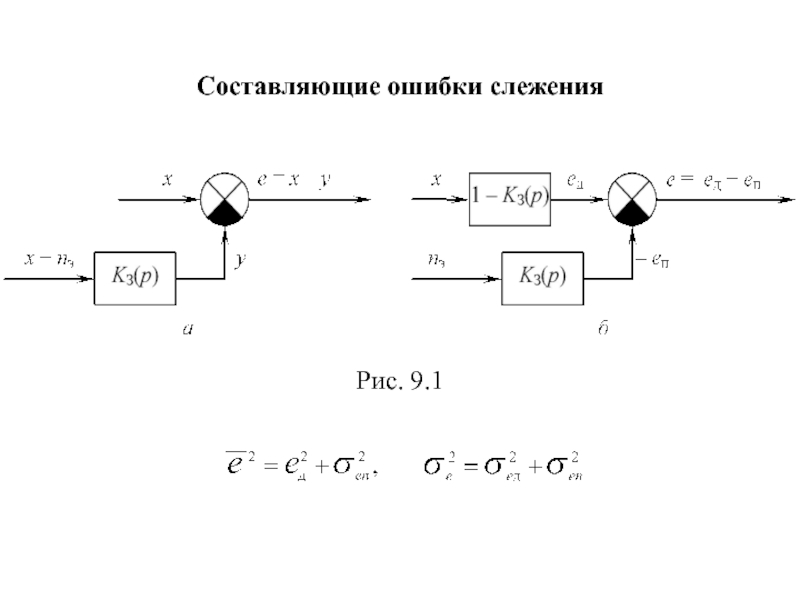
- 63. Составляющие ошибки слежения Рис. 9.1
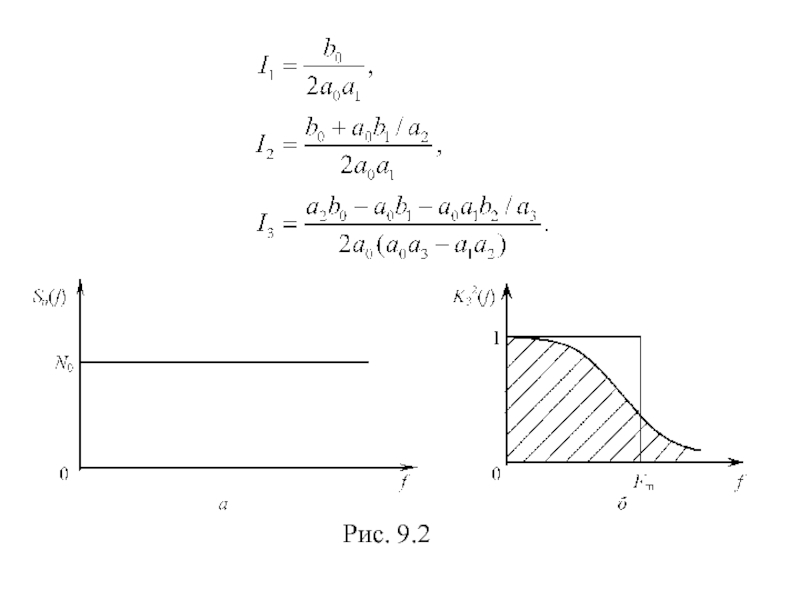
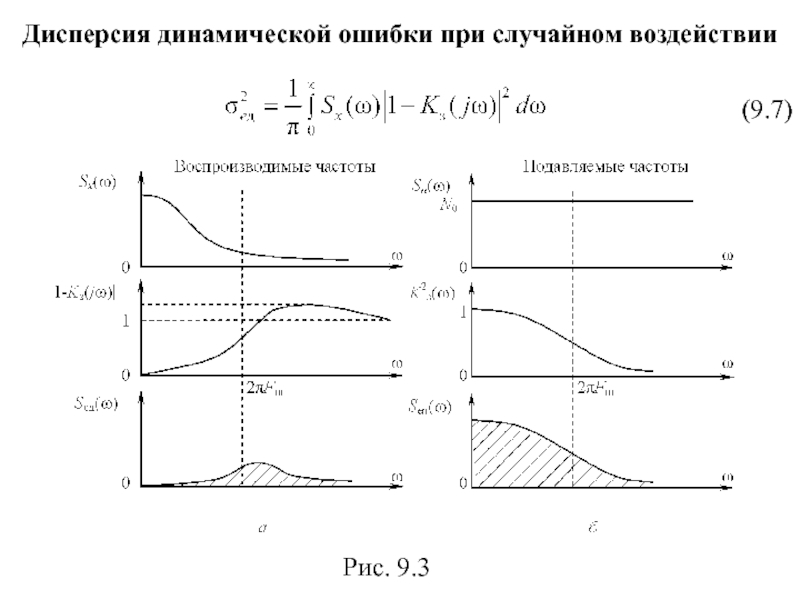
- 64. Дисперсия шумовой ошибки где Sэ(ω)=Sn(ω)/k2д − энергетический
- 65. Шумовая полоса замкнутой системы Для типовых систем
- 66. Рис. 9.2
- 67. Дисперсия динамической ошибки при случайном воздействии Рис. 9.3
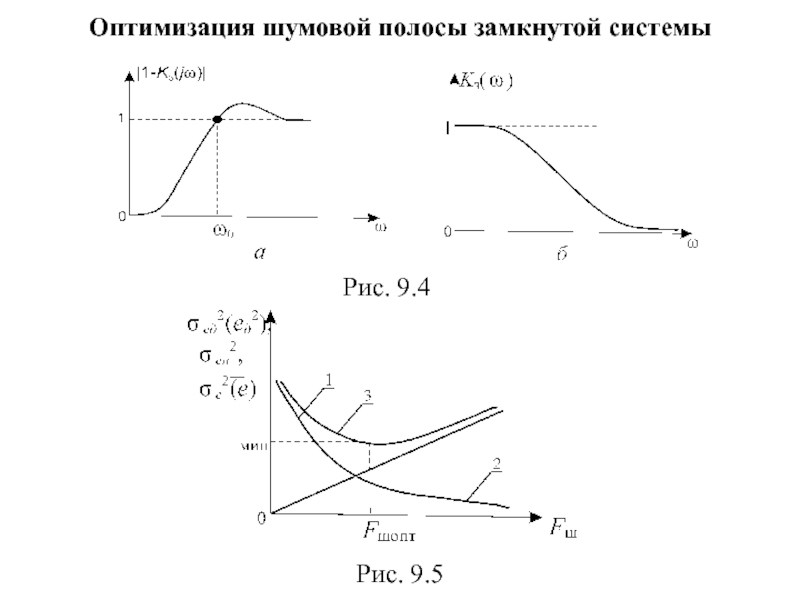
- 68. Оптимизация шумовой полосы замкнутой системы Рис. 9.4 Рис. 9.5
- 69. Тема 15: «Методы анализа нелинейных систем
- 70. Методы анализа нелинейных систем радиоавтоматики метод
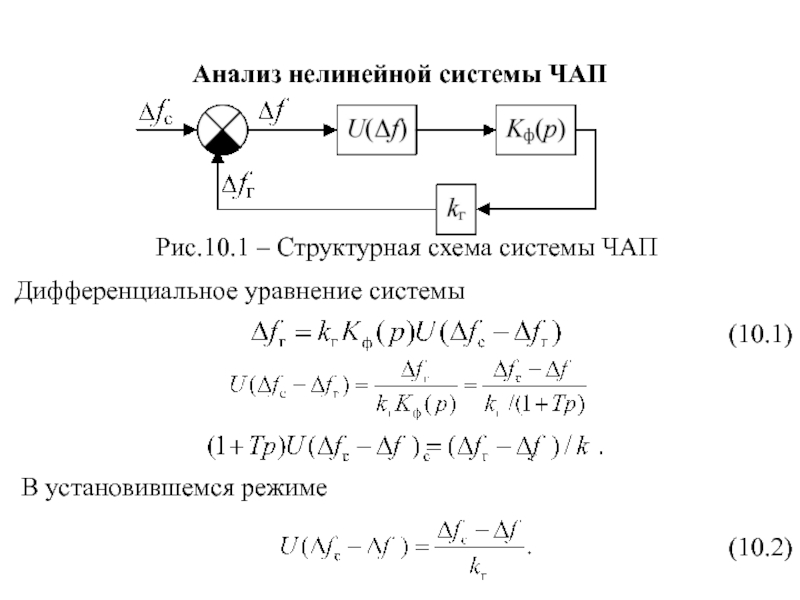
- 71. Анализ нелинейной системы ЧАП Рис.10.1 –
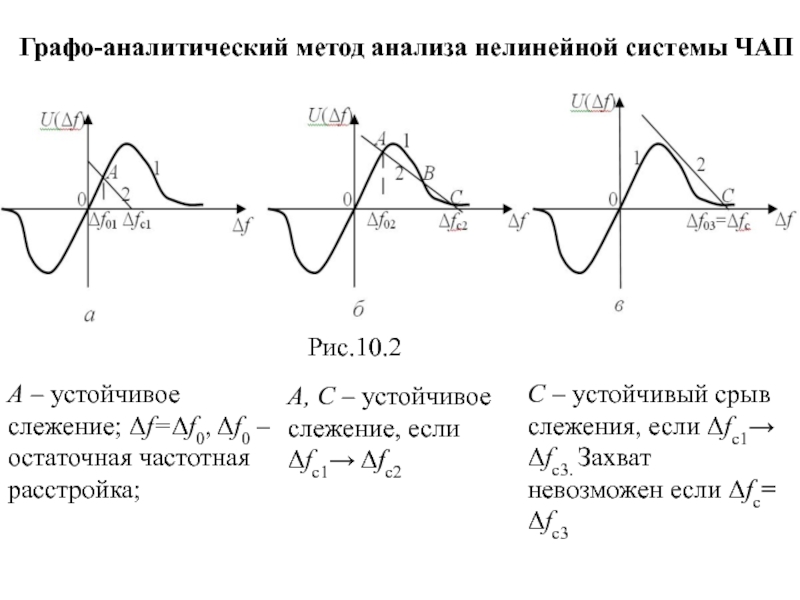
- 72. Графо-аналитический метод анализа нелинейной системы ЧАП A
- 73. Передаточная функция замкнутой (линеаризованной) системы
- 74. Графический метод определения полос захвата и удержания
- 75. Зависимость статической ошибки от частотной расстройки
- 76. Тема 16: «Анализ дискретных систем радиоавтоматики»
- 77. Математическое описание дискретных АС Дискретное преобразование
- 78. Обобщенная структурная схема линейной дискретной САУ Рис.11.1
- 79. Анализ точности дискретной САУ при детерминированном воздействии
- 80. Анализ точности дискретной САУ при воздействии помех
- 81. Тема 2: «Системы автоматической регулировки усиления
- 82. Система АРУ с управлением по рассогласованию
- 83. Амплитудные характеристики РУ Рис. 12.2 Кривая
- 84. Математическое описание системы АРУ Амплитудная характеристика линейного
- 85. Характеристика АД при линейном детектировании: где
- 86. Структурная схема системы АРУ как системы стабилизации Рис. 12.3
- 87. Тема 3: «Системы частотной автоподстройки (ЧАП)»
- 88. Функциональная схема системы частотной автоподстройки
- 89. Принцип действия системы ЧАП Пример. Стабилизация промежуточной
- 90. Рис. 13.2 – Дискриминационная характеристика
- 91. Тема 4: «Системы фазовой автоподстройки (ФАП)»
- 92. Применение системы ФАП следящие фильтры
- 93. Функциональная схема системы фазовой автоподстройки Рис.
- 94. Дискриминационная характеристика фазового дискриминатора uc(t)=umcsinϕc(t)=umcsin(ωct+ϕc0), uг(t)=umгcosϕг(t)=umгcos(ωгt+ϕг0). Рис. 14.2
- 95. Рис. 14.3 tз – время захвата;
- 96. Рис. 14.4 Δf0>Δfз – режим биений.
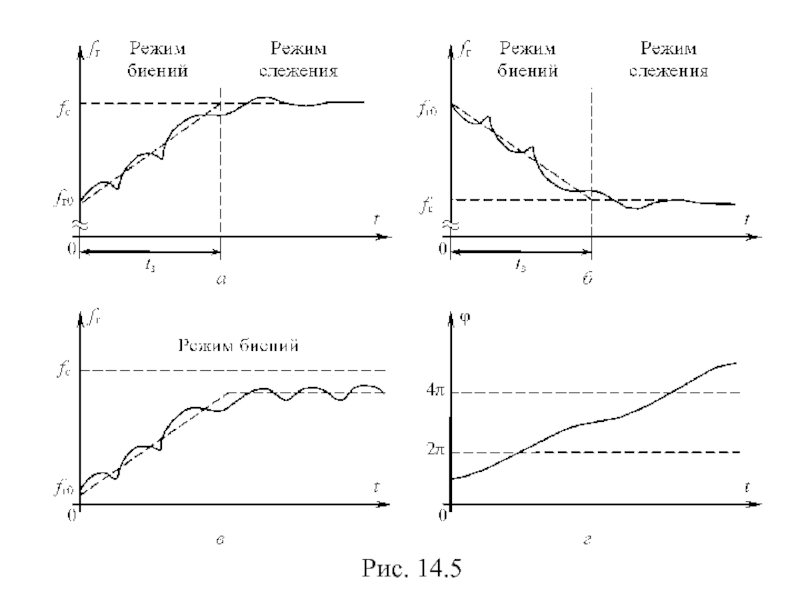
- 97. Рис. 14.5
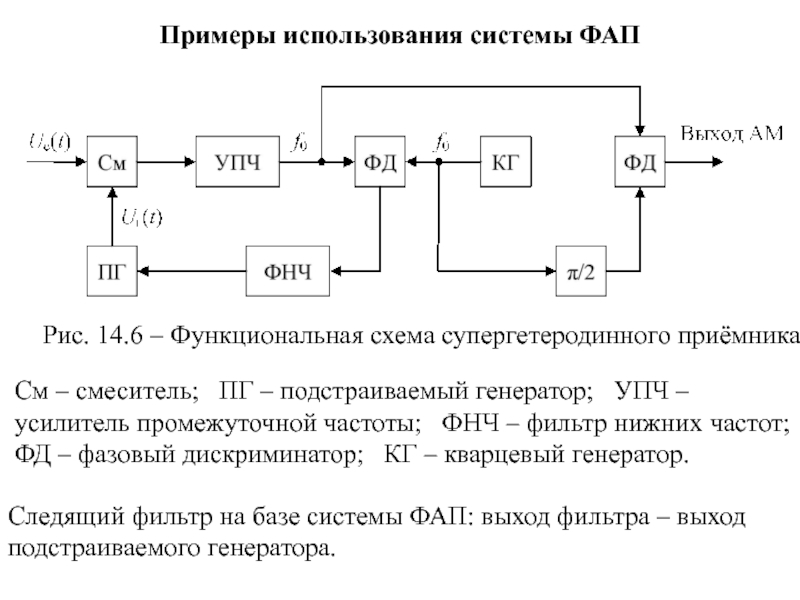
- 98. Примеры использования системы ФАП Рис. 14.6
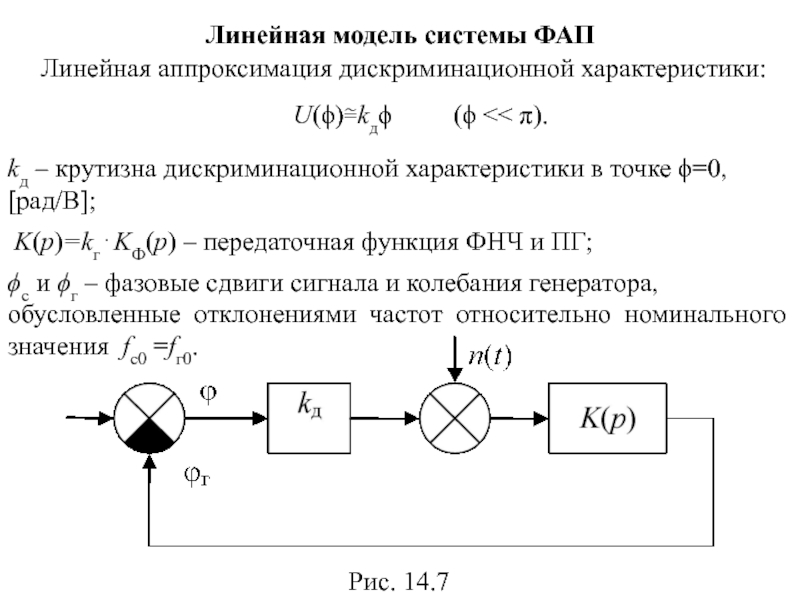
- 99. Линейная модель системы ФАП Линейная аппроксимация дискриминационной характеристики: U(ϕ)≅kдϕ (ϕ
- 100. Тема 5: «Системы слежения за задержкой
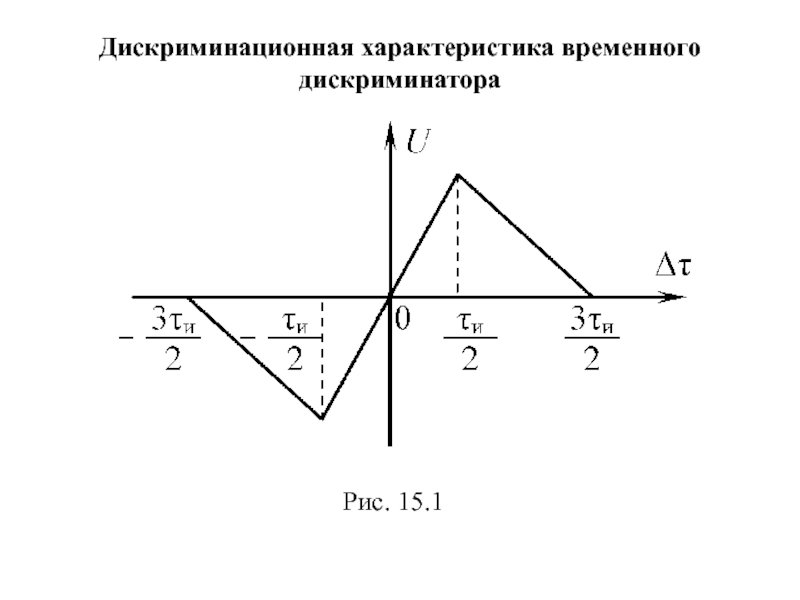
- 101. Дискриминационная характеристика временного дискриминатора Рис. 15.1
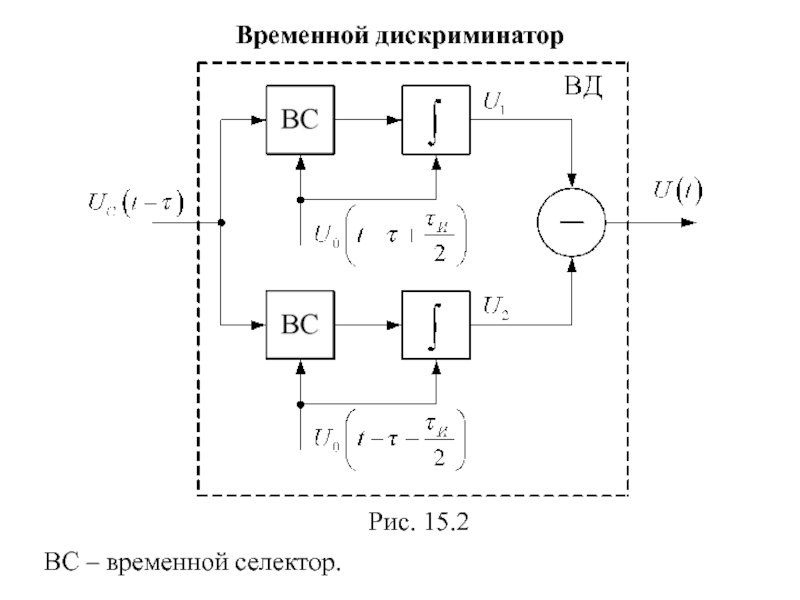
- 102. Временной дискриминатор Рис. 15.2 ВС – временной селектор.
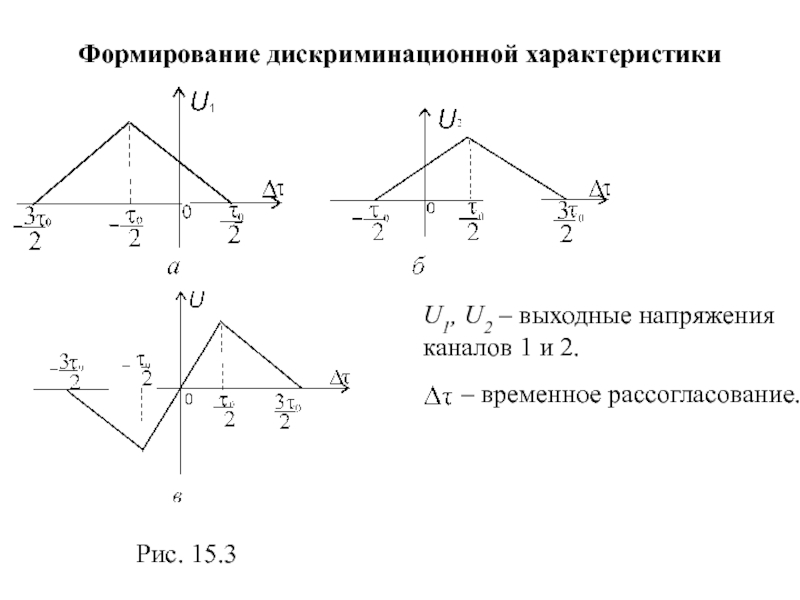
- 103. Формирование дискриминационной характеристики
- 104. Структурная схема системы слежения за задержкой Временное
- 105. Регулировочная характеристика схемы управляемой задержки где
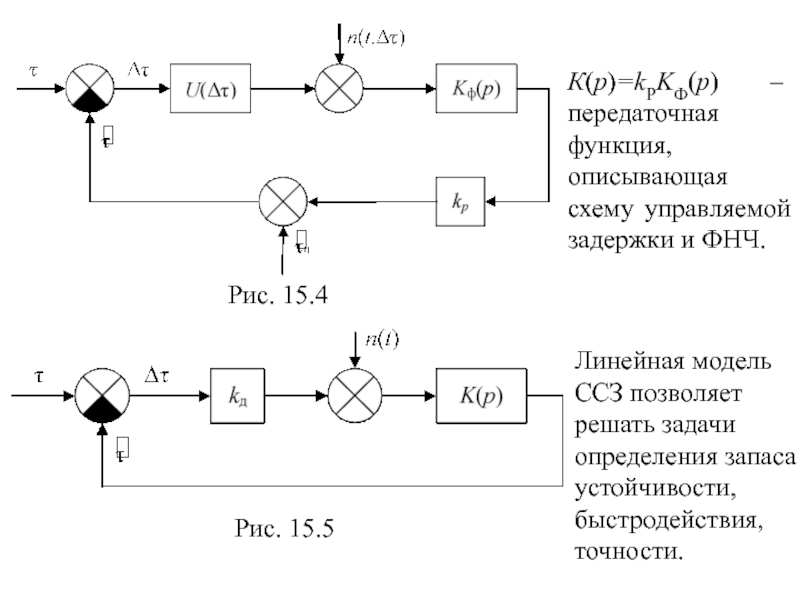
- 106. Рис. 15.4 Рис. 15.5 К(p)=kPKФ(p)
- 107. Тема 6: «Системы слежения за направлением
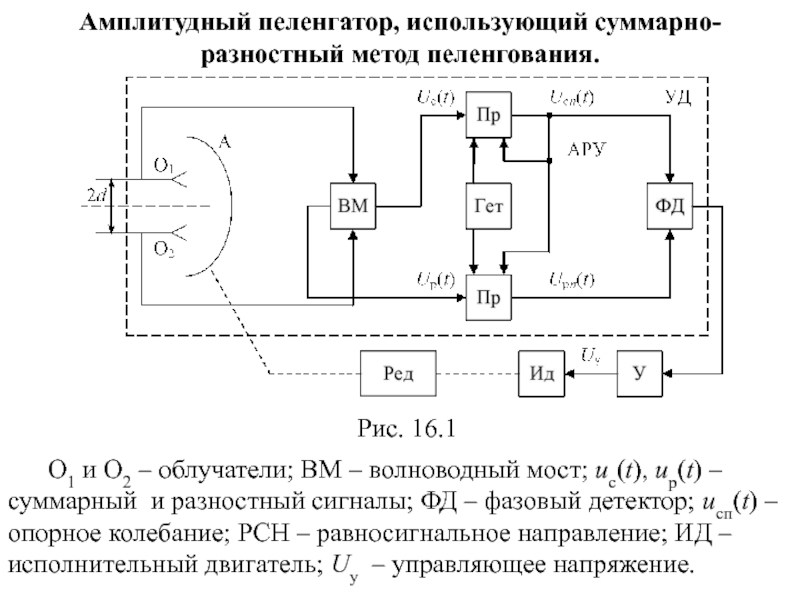
- 108. Амплитудный пеленгатор, использующий суммарно-разностный метод пеленгования.
- 109. Диаграмма направленности антенны Дискриминационная характеристика
- 110. Угловое рассогласование где αц – азимут (пеленг)
- 111. Управляющее напряжение Uу(t)=kуUд(t), (16.6) где Ωд(t)
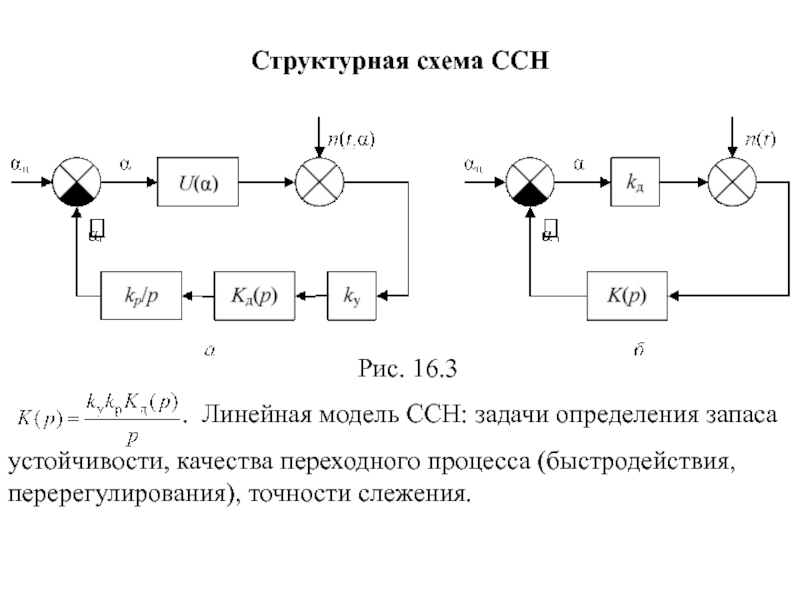
- 112. Структурная схема ССН Рис. 16.3
Слайд 1Федеральное государственное автономное образовательное учреждение высшего образования
«Сибирский федеральный университет»
РАДИОАВТОМАТИКА
Демонстрационная презентация лекционного
Красноярск
2017
Слайд 2Предмет и задачи курса
Предмет изучения дисциплины – системы автоматического управления (САУ),
Основными задачами курса являются изучение основ теории автоматического управления, принципов действия типовых систем автоматического управления, методов их анализа, синтеза и оптимизации.
Слайд 3Сходство и различие радиотехнических САУ и других автоматических систем
Сходство радиотехнических САУ
Слайд 4Краткая история развития систем автоматического управления
Первые радиотехнические САУ – системы автоматической
Большое применение находят системы частотной и фазовой автоподстройки частоты (ЧАП и ФАП): для стабилизации промежуточной частоты приемников, в качестве демодуляторов сигналов с частотной и фазовой модуляцией, в синтезаторах частот, в следящих измерителях координат и скорости подвижных объектов.
В радиолокации и радионавигации широкое применение находят системы слежения за задержкой сигнала (ССЗ), на основе которых строятся следящие измерители дальности. Кроме того, они используются в радиосвязи в качестве систем синхронизации.
Системы слежения за направлением (ССН) применяются в радиолокации и радионавигации в качестве следящих измерителей угловых координат, в радиоуправлении крылатыми ракетами, а также в радиосвязи (наведение направленных антенн).
Слайд 5Тема 1: «Общая характеристика систем автоматического
управления»
Содержание
1. Основные понятия и определения
2.
3. Классификация САУ
4. Примеры характеристик нелинейных звеньев
Слайд 6
Основные понятия и определения
Автоматика – отрасль науки и техники, охватывающая теорию
Автоматическое регулирование – поддержание заданного значения какой - либо физической величины без непосредственного участия человека с помощью специальных автоматических регуляторов.
Автоматическое управление – изменение по некоторому закону какой - либо физической величины без непосредственного участия человека с помощью специальных автоматических управителей.
Элемент автоматики – звено автоматической системы, выполняющее определенную функцию и характеризующееся назначением, принципом действия, устройством (конструкцией), электронной схемой.
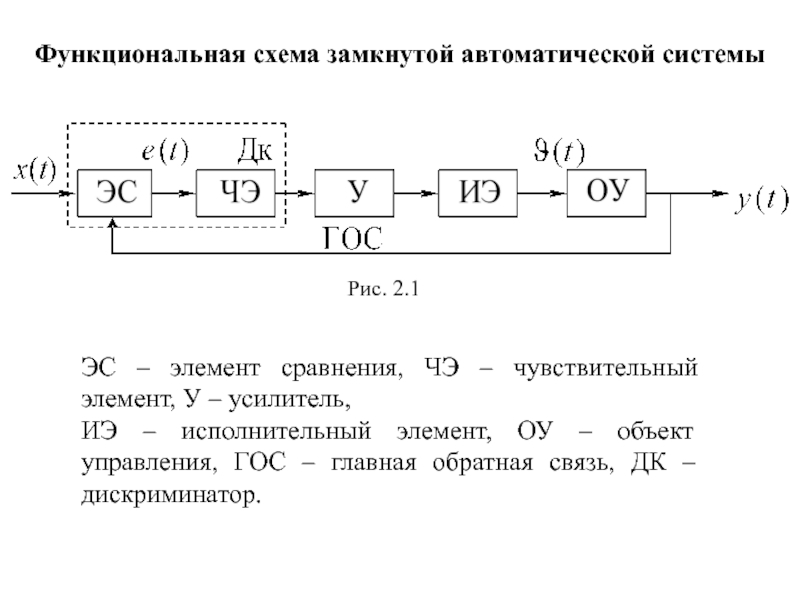
Слайд 7Функциональная схема замкнутой автоматической системы
ЭС – элемент сравнения, ЧЭ – чувствительный
ИЭ – исполнительный элемент, ОУ – объект управления, ГОС – главная обратная связь, ДК – дискриминатор.
Рис. 2.1
Слайд 11Статическая характеристика – алгебраическое уравнение y=ƒ(x) (для описания безынерционных звеньев);
Динамические характеристики
Пример: RC-фильтр нижних частот (ФНЧ):
Слайд 12Литература
В.Н. Бондаренко
Основы автоматики : учеб. пособие, 2004
либо – Радиоавтоматика: учеб. пособие,
Радиоавтоматика. Методические указания по курсовому проектированию, 2011
Радиоавтоматика. учеб.-метод. пособие для лаб. практикума, 2012
Радиоавтоматика. учеб.-метод. пособие для практ. занятий, 2012
Дополнительная литература:
Соколов А. И. Радиоавтоматика : учеб. пособие, 2011.
Первачев, С.В. Радиоавтоматика. / М.: Радио и связь, 1982 – с., 296.
Чердынцев, В.А. Радиотехнические системы. / Минск: Высш. школа, 1988. – 368 с.
Бесекерский, В.А. Радиоавтоматика / М.: Высш. школа, 1985.
Коновалов, Г.Ф. Радиоавтоматика / М.: Высш. школа, 1990.
Бесекерский, В.А. Теория систем автоматического управления / СПб. : Профессия, 2003.
Ерофеев, А.А. Теория автоматического управления / СПб. : Политехника, 1998.
Шавров, А.В. Автоматика / М. : Колос, 2000.
Слайд 13
Тема 2: «Типовые звенья систем автоматического
управления»
Содержание
Интегрирующее звено
Частотные и временные характеристики
Форсирующее звено
Характеристики форсирующего звена
Способы реализации форсирующего звена
Колебательное звено
Частотные характеристики колебательного звена
Переходная характеристика колебательного звена
Слайд 14Интегрирующее звено
Уравнение динамики интегрирующего звена
,
где kи – коэффициент передачи, с –1.
Передаточная функция
, (7.2)
Частотные характеристики
, (7.3)
. (7.4)
ЛАХ: L(ω)=20lgK(ω)=20lgkи – 20lgω.
Слайд 16Форсирующее звено
где k – коэффициент передачи звена, Т – постоянная времени.
Передаточная
К(р)=k(1+Тр). (7.6)
АЧХ и ФЧХ звена
ϕ(ω)=arctgωT. (7.8)
Слайд 17Характеристики форсирующего звена
Рис. 7.3
L(ω)=20lgk+20lg(1+ω2T2)1/2. (7.9)
L′(ω)=20lgk при
L″(ω)=20lgk+20lgωT при ω > 1/Т. (7.10)
Рис. 7.4 – Переходная характеристика форсирующего звена
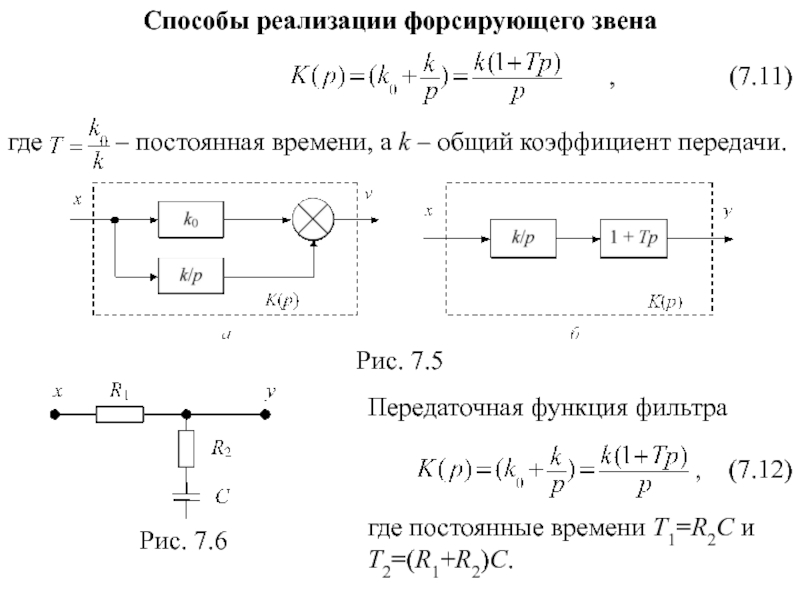
Слайд 18Способы реализации форсирующего звена
Рис. 7.5
Рис. 7.6
Передаточная функция фильтра
где постоянные времени Т1=R2C
Слайд 19Колебательное звено
Уравнение динамики
где Т – постоянная времени, γ – коэффициент затухания
Передаточная функция
Частотные характеристики колебательного звена
где ω0=1/Т − собственная частота.
Слайд 21Резонансная частота
При γ ≥ 1 звено апериодическое.
ЛАХ
L′(ω) 20lgk.
L″(ω) 20lgk – 40lg(ω/ω0). (7.19)
Слайд 23Тема 8: «Передаточные функции систем
радиоавтоматики»
Содержание
Обобщенная функциональная схема САУ
Обобщенная структурная схема
Дискриминационная характеристика
Флуктуационная характеристика
Правила преобразования структурных схем
6. Передаточные функции замкнутой системы
7. САУ как фильтр
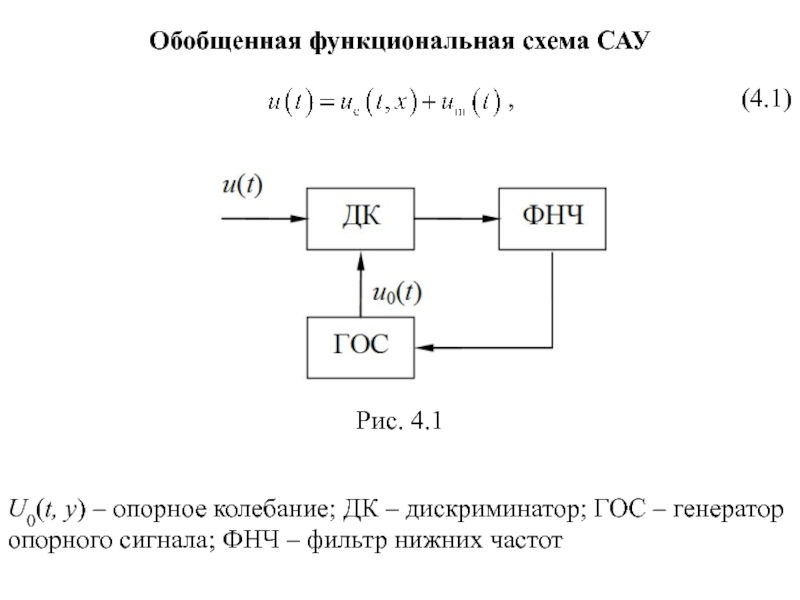
Слайд 24Обобщенная функциональная схема САУ
U0(t, y) – опорное колебание; ДК – дискриминатор;
Рис. 4.1
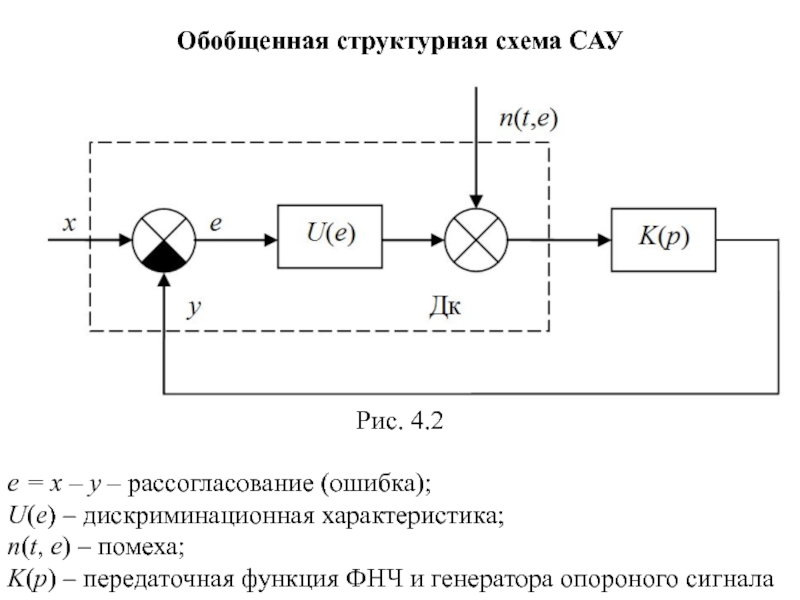
Слайд 25Обобщенная структурная схема САУ
e = x – y – рассогласование (ошибка);
U(e)
n(t, e) – помеха;
K(p) – передаточная функция ФНЧ и генератора опороного сигнала
Рис. 4.2
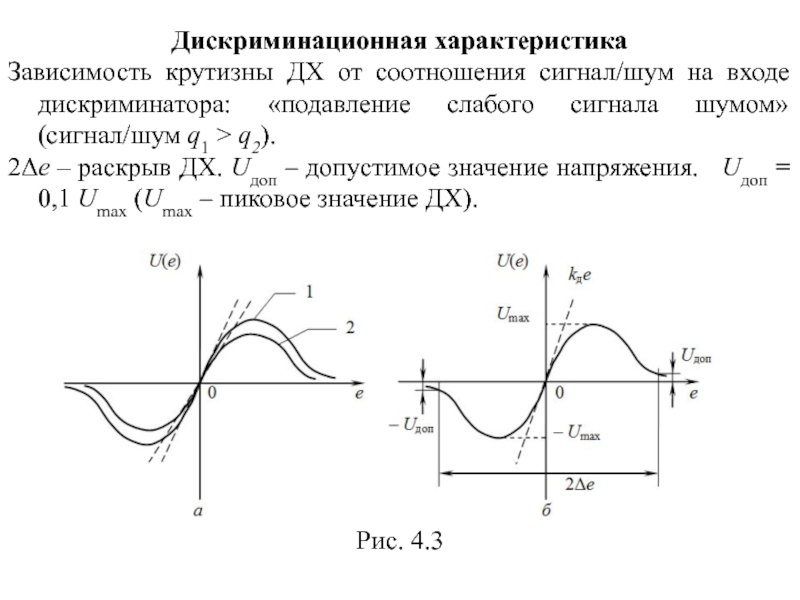
Слайд 26Дискриминационная характеристика
Зависимость крутизны ДХ от соотношения сигнал/шум на входе дискриминатора: «подавление
2Δe – раскрыв ДХ. Uдоп – допустимое значение напряжения. Uдоп = 0,1 Umax (Umax – пиковое значение ДХ).
Рис. 4.3
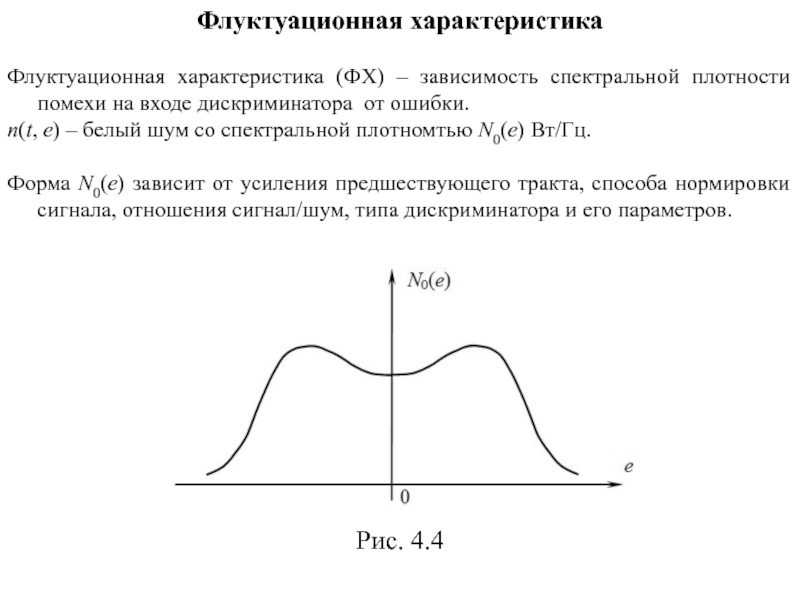
Слайд 27Флуктуационная характеристика
Флуктуационная характеристика (ФХ) – зависимость спектральной плотности помехи на входе
n(t, e) – белый шум со спектральной плотномтью N0(e) Вт/Гц.
Форма N0(e) зависит от усиления предшествующего тракта, способа нормировки сигнала, отношения сигнал/шум, типа дискриминатора и его параметров.
Рис. 4.4
Слайд 28Дифференциальное уравнение системы
y(t) = K(p)[U(e)+ n(t, e)].
Линеаризация дискриминационной характеристики (e → 0)
y(t) =kд K(p)e(t)+K(p) n(t). (4.3)
Рис. 4.5
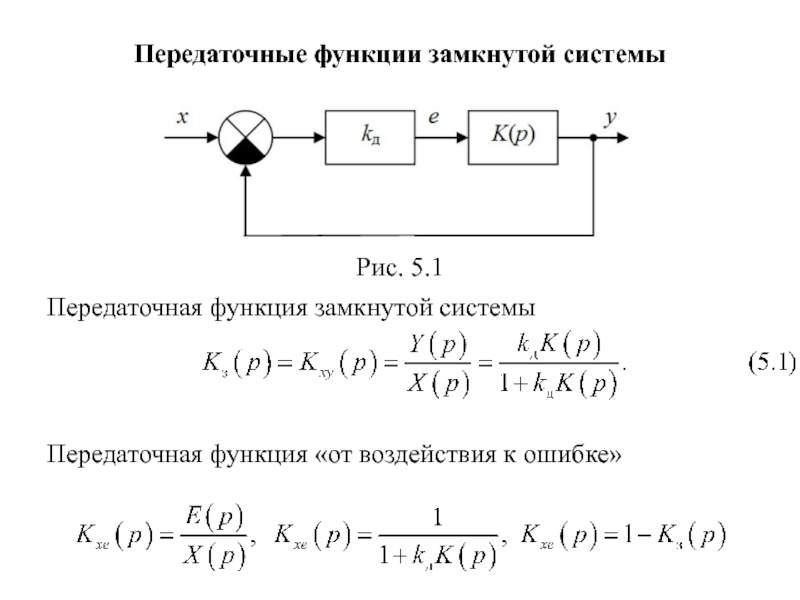
Слайд 31Передаточные функции замкнутой системы
Передаточная функция замкнутой системы
Передаточная функция «от воздействия к
Рис. 5.1
Слайд 32САУ как фильтр
Рис. 5.2
Kз(jω) – комплексный коэффициент передачи (АФХ).
Модуль АФХ Kз(ω)
Экспериментальное опретеделение АЧХ замкнутой системы:
x(t) = Xmsin(ωt). Xm – «амплитуда» (девиация частоты, индекс фазовой модуляции, …). АЧХ замкнутой системы – зависимость от частоты отношения «амплитуды» Ym выходной переменной к «амплитуде» Xm входной переменой.
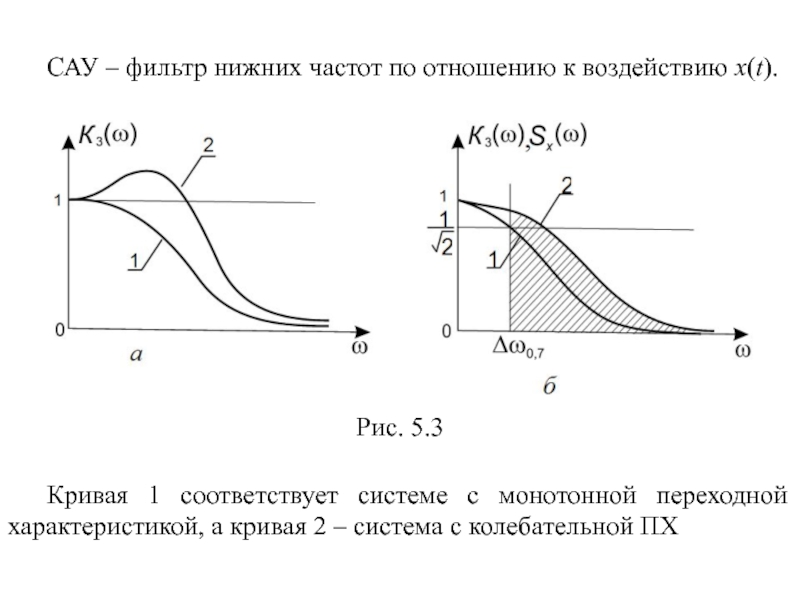
Слайд 33САУ – фильтр нижних частот по отношению к воздействию x(t).
Рис. 5.3
Кривая
Слайд 34
Тема 9: «Устойчивость автоматических систем»
Содержание
Общие требования к устойчивости систем
Алгебраические критерии устойчивости
Частотные
Запас устойчивости
Слайд 35Общие требования к устойчивости систем
Характеристическое уравнение замкнутой системы:
Однородное дифференциальное уравнение:
где а0,
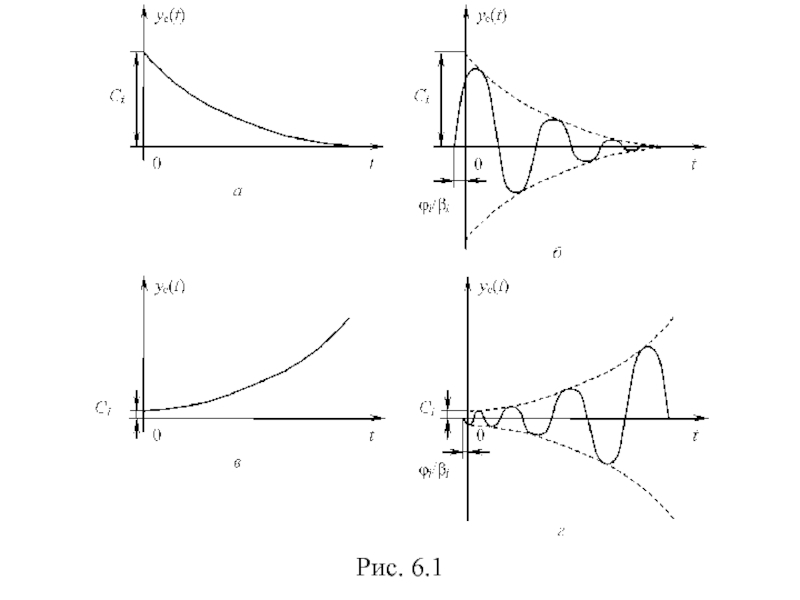
отрицательные вещественные корни (рис. 6.1, а);
комплексные корни с отрицательной вещественной частью (рис. 6.1, б);
положительный вещественный корень (рис. 6.1, в);
комплексные корни с положительной вещественной частью (рис. 6.1, г).
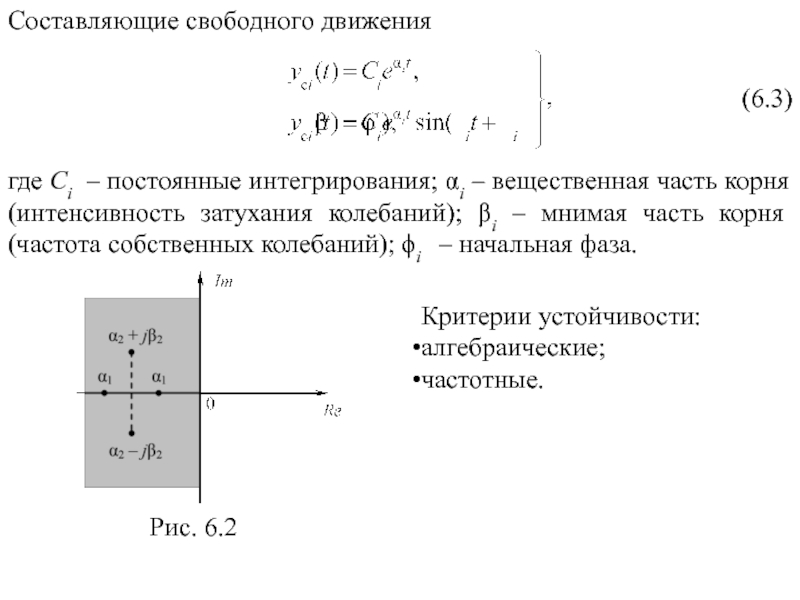
Слайд 37Составляющие свободного движения
где Сi – постоянные интегрирования; αi – вещественная часть
Рис. 6.2
Критерии устойчивости:
алгебраические;
частотные.
Слайд 38Алгебраические критерии устойчивости
Критерий Гурвица: главный определитель, а также все его диагональные
Главный определитель Гурвица для уравнения n-й степени:
Если все миноры, кроме предпоследнего, положительны, а минор Δn – 1 равен нулю, то система находится на границе устойчивости.
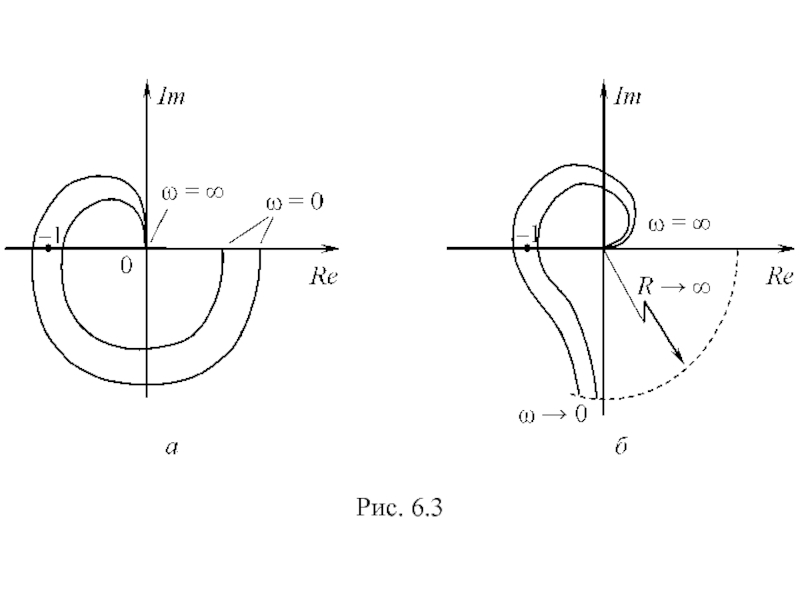
Слайд 39Частотные критерии устойчивости
Критерий Найквиста: замкнутая система устойчива, если АФХ разомкнутой системы
АФХ – кривая на комплексной плоскости, представляющая геометрическое место конца вектора комплексного коэффициента передачи Kр(jω) при изменении частоты от нуля до бесконечности (годографом).
Для астатических (рис. 6.3, б) систем АФХ дополняется дугой бесконечно большого радиуса и определется её расположение относительно точки (–1, j0).
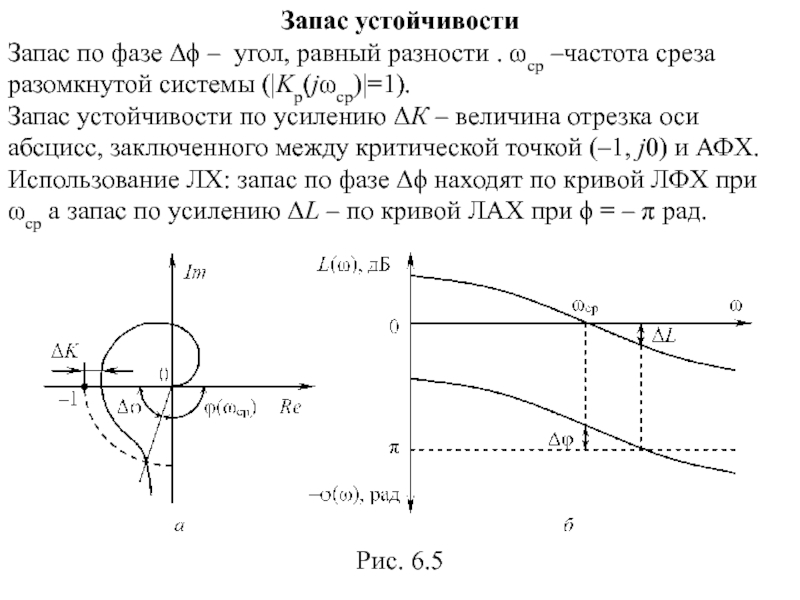
Слайд 42Запас устойчивости
Запас по фазе Δϕ – угол, равный разности . ωср
Запас устойчивости по усилению ΔК – величина отрезка оси абсцисс, заключенного между критической точкой (–1, j0) и АФХ.
Использование ЛХ: запас по фазе Δϕ находят по кривой ЛФХ при ωср а запас по усилению ΔL – по кривой ЛАХ при ϕ = – π рад.
Рис. 6.5
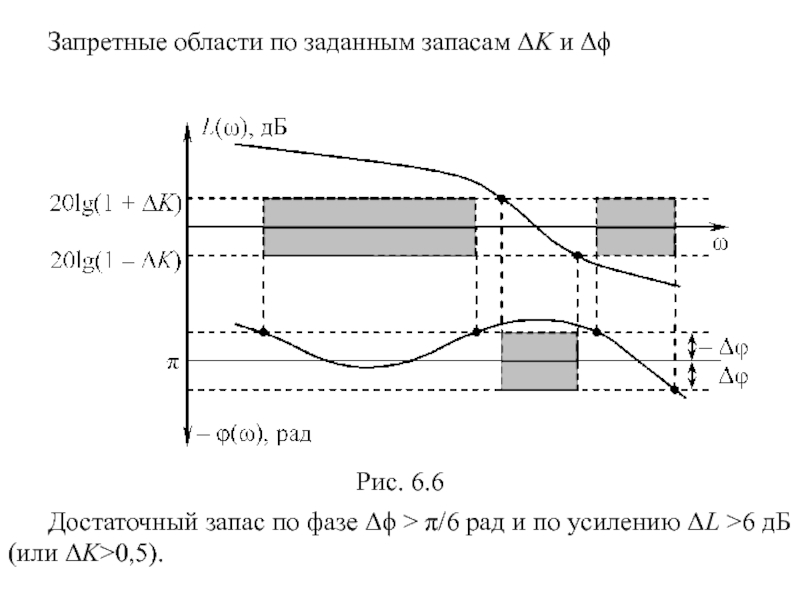
Слайд 43Запретные области по заданным запасам ΔK и Δϕ
Рис. 6.6
Достаточный запас по
Слайд 44
Тема 10: «Оценка качества автоматических систем в переходном режиме»
Содержание
Цифровое моделирование непрерывных
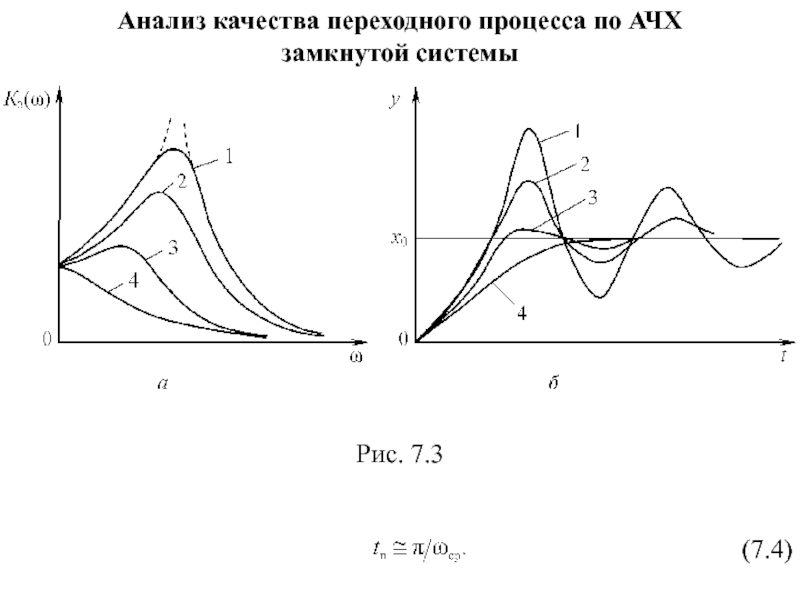
Анализ качества переходного процесса по АЧХ замкнутой системы
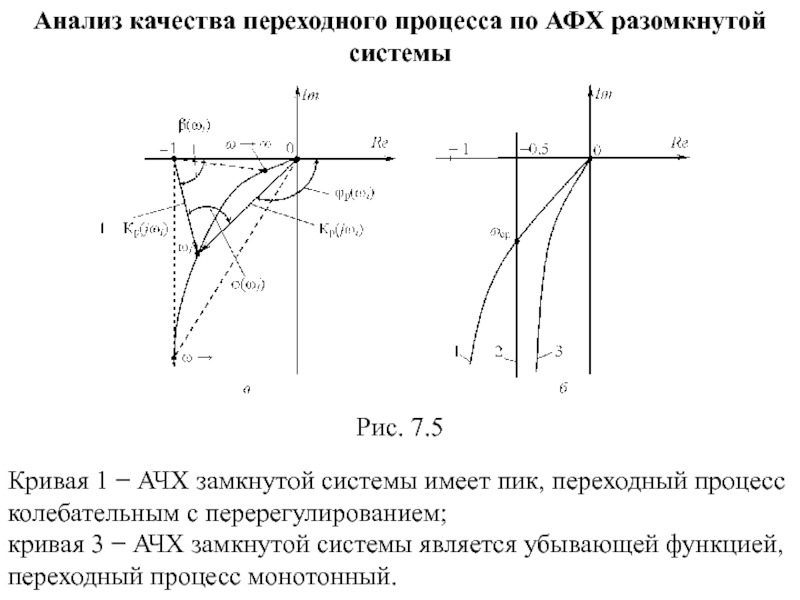
Анализ качества переходного процесса по АФХ разомкнутой системы
Оценка качества переходного процесса по ЛАХ разомкнутой системы
ЛАХ типовых систем
Слайд 45Типовые воздействия в виде детерминированных функций времени:
постоянное (ступенчатое),
линейное,
квадратичное.
Методы анализа качества переходного
прямые (по переходной характеристике замкнутой системы),
косвенные (по АЧХ замкнутой системы, по АФК разомкнутой системы, по ЛАХ разомкнутой системы).
Слайд 46
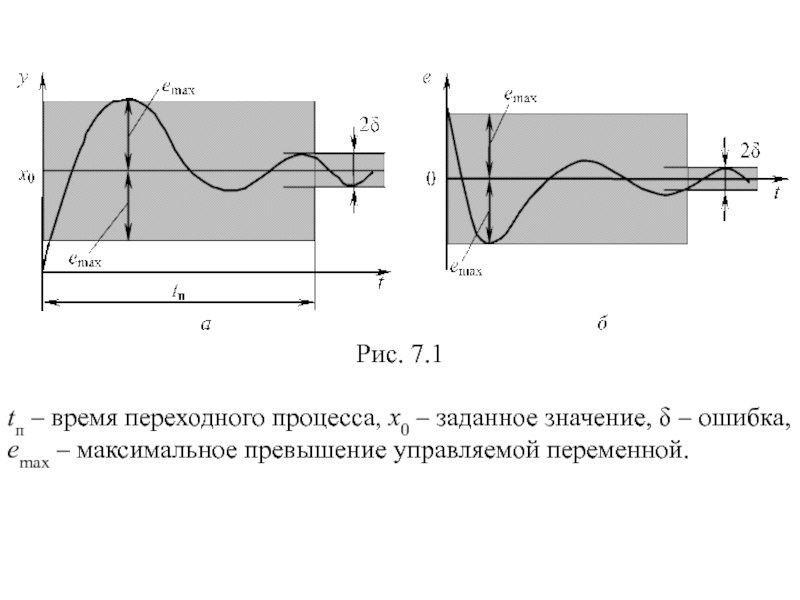
Рис. 7.1
tп – время переходного процесса, x0 – заданное значение, δ
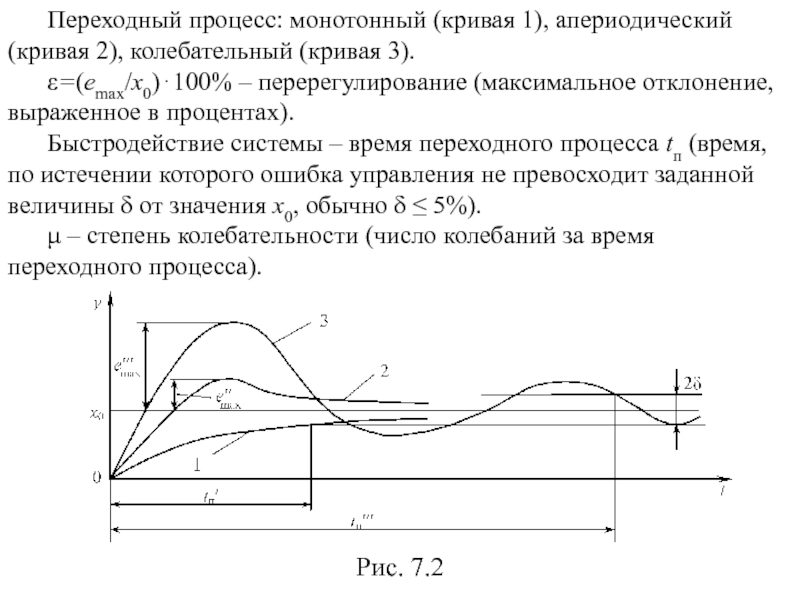
Слайд 47Переходный процесс: монотонный (кривая 1), апериодический (кривая 2), колебательный (кривая 3).
ε=(emax/x0)⋅100%
Быстродействие системы – время переходного процесса tп (время, по истечении которого ошибка управления не превосходит заданной величины δ от значения x0, обычно δ ≤ 5%).
μ – степень колебательности (число колебаний за время переходного процесса).
Рис. 7.2
Слайд 48Цифровое моделирование непрерывных САУ
Разностное уравнение – программа рекуррентного вычисления переходного процесса.
Дискретная
где T − интервал дискретизации, z=e pT − переменная Z – преобразования (z – 1=e – pT − оператор задержки на T).
Разностное уравнение
где y[k] − текущее значение управляемой переменной, x[k–i] и y[k–i] − предыдущие значения процессов на (k–i)-м шаге.
Слайд 51
Рис. 7.5
Кривая 1 − АЧХ замкнутой системы имеет пик, переходный процесс
кривая 3 − АЧХ замкнутой системы является убывающей функцией, переходный процесс монотонный.
Анализ качества переходного процесса по АФХ разомкнутой системы
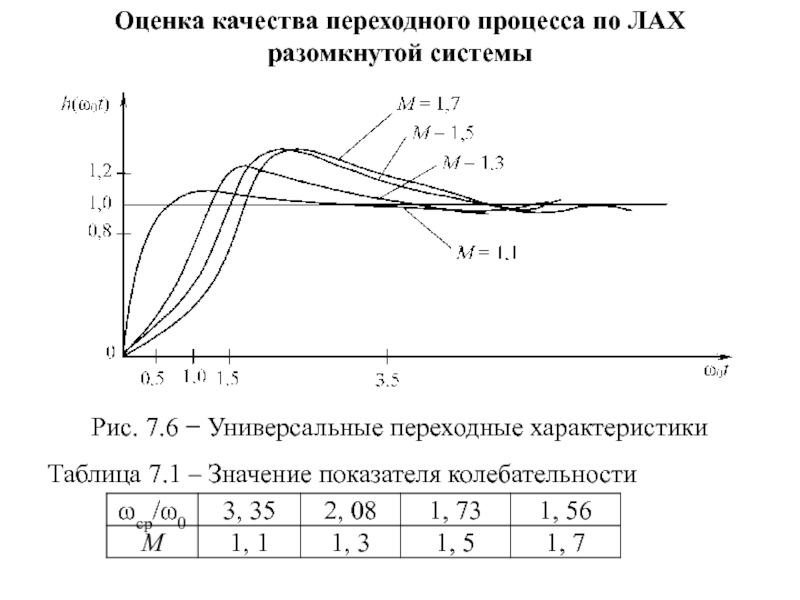
Слайд 52Оценка качества переходного процесса по ЛАХ
разомкнутой системы
Рис. 7.6 − Универсальные переходные
Таблица 7.1 – Значение показателя колебательности
Слайд 54
Тема 11: «Точность автоматических систем при типовых воздействиях»
Содержание
Статические ошибки
Динамические ошибки
Слайд 55Точность САУ при типовых воздействиях
Точность АС – величина ошибки в установившемся
Детерминированные воздействия:
постоянное (ступенчатое),
линейное,
квадратичное.
Передаточная функция, описывающая систему радиоавтоматики:
где Ki − общее усиление разомкнутой системы, i – число интегрирующих звеньев, определяющее порядок астатизма системы;
Слайд 56Статические ошибки
Статическая ошибка – ошибка системы при постоянном (ступенчатом) воздействии x(t)=x0=const.
Ошибка
Ошибка астатических систем (i ≥ 1) при постоянном воздействии
Слайд 57Динамические ошибки
Динамическая ошибка eд(t) – ошибка, характеризующая точность замкнутой системы при
где x0 − начальное значение, − скорость изменения, − ускорение и т. д.
Выражение для ошибки в операторной форме:
где C0, C1, C2, … − коэффициенты ошибок.
Слайд 58Установившееся значение ошибки
Для статических систем (i=0) C0=1/(1+K0), для астатических систем C0=0.
Динамические ошибки типовых систем при линейном воздействии (изменение с постоянной скоростью) x(t)=νxt.
Динамическая ошибка (ошибка по скорости):
Для статической системы она равна
Слайд 59Установившееся значение ошибки
i = 1 (астатическая система первого порядка):
C1=1/K1, так как
Скоростная ошибка системы первого порядка астатизма eд=νx/K1 определяется усилением разомкнутой системы K1 и не зависит от времени. Параметр K1, имеющий размерность c –1, называется добротностью системы по скорости.
Слайд 60Для астатической системы второго порядка скоростная ошибка равна нулю (C0=C1=0).
Динамические ошибки
Для динамической ошибки (ошибки по ускорению)
Для статической системы ошибка по ускорению равна
Для системы первого порядка астатизма ошибка по ускорению равна
Слайд 61
Откуда C2/2=1/K2, так как C0=C1=0.
Ошибка по ускорению в системе второго
Для астатической системы второго порядка ошибка по ускорению равна
Слайд 62Тема 12: «Точность автоматических систем при воздействии помех»
Содержание
Составляющие ошибки слежения
Дисперсия динамической
Оптимизация шумовой полосы замкнутой системы
Слайд 64Дисперсия шумовой ошибки
где Sэ(ω)=Sn(ω)/k2д − энергетический спектр эквивалентного шума, Sn(ω) –
Эквивалентный шум – белый шум со спектральной плотностью мощности Sэ(f)=Nэ=N0/k2д, размерность [х]2/Гц ([х] – размерность задающего воздействия).
Дисперсия шумовой ошибки
Слайд 65Шумовая полоса замкнутой системы
Для типовых систем радиоавтоматики определенный интеграл в (6.16)
где полиномы An(jω) и Bn(ω)
Слайд 69
Тема 15: «Методы анализа нелинейных систем
радиоавтоматики»
Содержание
Анализ нелинейной системы ЧАП
Графо-аналитический
Графический метод определения полос захвата и удержания
Зависимость статической ошибки от частотной расстройки
Слайд 70Методы анализа нелинейных систем радиоавтоматики
метод фазовой плоскости
метод кусочно-линейной аппроксимации
метод гармонической линеаризации
метод
метод моделирования на ЭВМ
Нелинейные режимы работы АС:
Поиск – устранение начальной расстройки (уменьшение ее до значений, определяемых полосой захвата). (|e|
Полоса захвата характеризует способность захватывать сигнал и осуществлять слежение при максимально допустимой расстройке (2eдоп).
Слайд 71Анализ нелинейной системы ЧАП
Рис.10.1 – Структурная схема системы ЧАП
Дифференциальное уравнение системы
В
Слайд 72Графо-аналитический метод анализа нелинейной системы ЧАП
A – устойчивое слежение; Δf=Δf0, Δf0
A, C – устойчивое слежение, если Δfc1→ Δfc2
С – устойчивый срыв слежения, если Δfc1→ Δfc3. Захват невозможен если Δfc= Δfc3
Рис.10.2
Слайд 73Передаточная функция замкнутой (линеаризованной) системы
n=1. Необходимое и достаточное условие устойчивости: >0,
φi : φ1 =0, φ2= π, φ3= π.
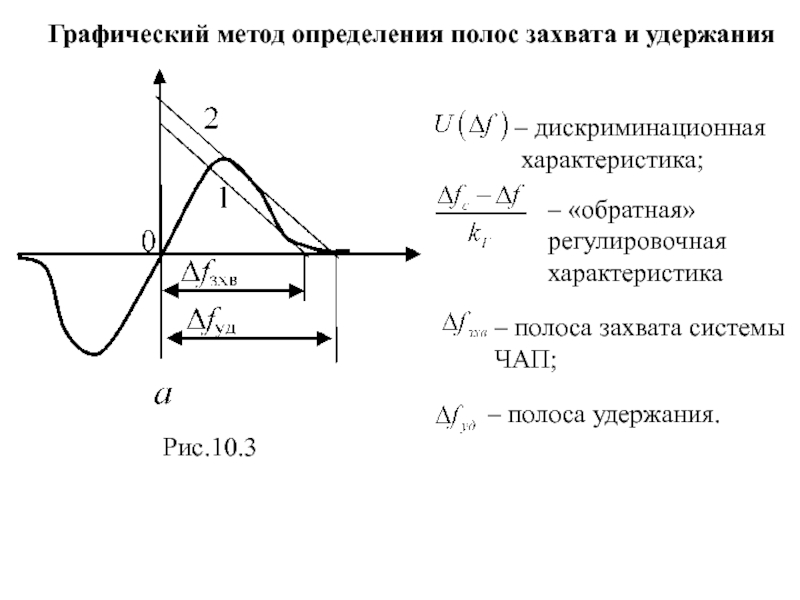
Слайд 74Графический метод определения полос захвата и удержания
– дискриминационная
характеристика;
– «обратная» регулировочная
– полоса захвата системы ЧАП;
– полоса удержания.
Рис.10.3
Слайд 75
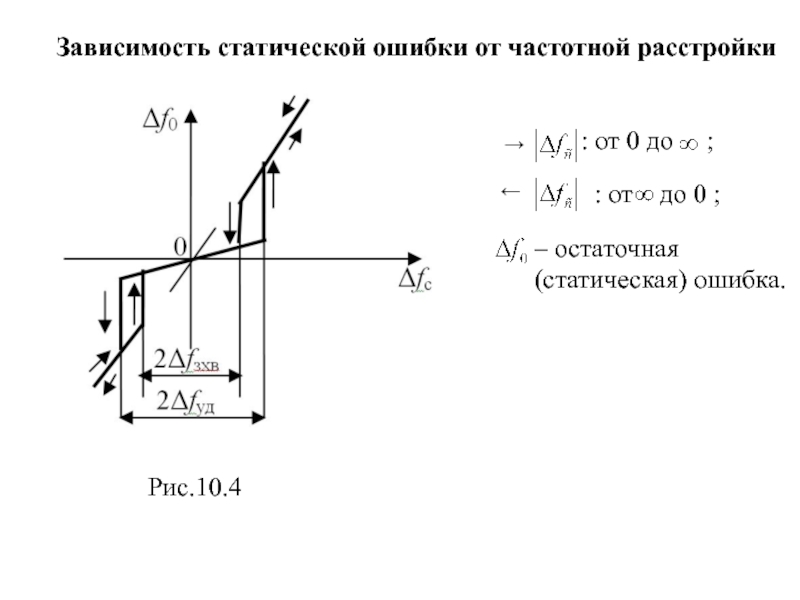
Зависимость статической ошибки от частотной расстройки
Рис.10.4
→
: от 0 до
←
: от до 0 ;
– остаточная (статическая) ошибка.
Слайд 76
Тема 16: «Анализ дискретных систем радиоавтоматики»
Тема 17: «Показатели качества управления дискретных
Содержание
Математическое описание дискретных САУ
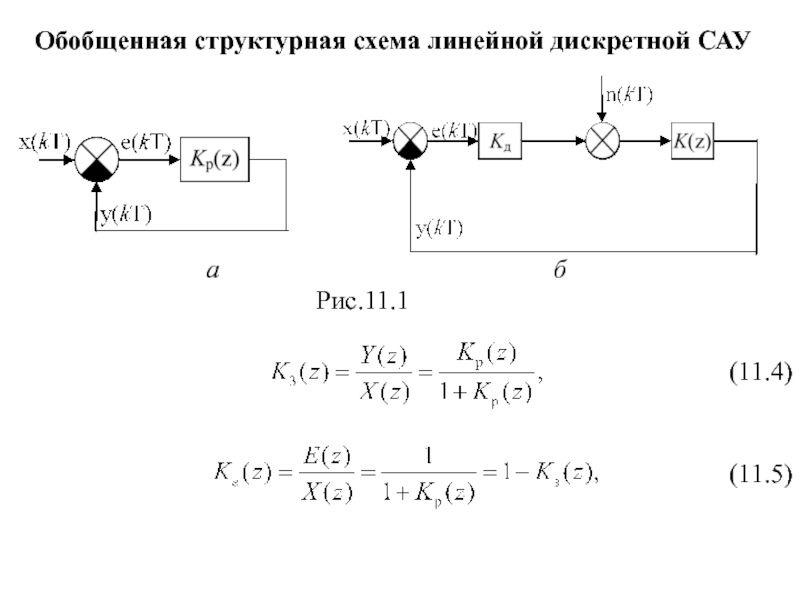
Обобщенная структурная схема линейной дискретной САУ
Анализ точности дискретной САУ при детерминированном воздействии
Анализ точности дискретной САУ при воздействии помех
Слайд 77Математическое описание дискретных АС
Дискретное преобразование Лапласа записывается в виде
Х(z) – Z-преобразование
Слайд 79Анализ точности дискретной САУ при детерминированном
воздействии
С0, С1 и С2–коэффициенты ошибок по
Слайд 80Анализ точности дискретной САУ при воздействии помех
Результирующая среднеквадратическая ошибка
eд – математическое
Дисперсия ошибки
Se(w) – спектральная плотность ошибки, w – псевдочастота.
Слайд 81
Тема 2: «Системы автоматической регулировки усиления (АРУ)»
Содержание
Система АРУ с управлением по
Амплитудные характеристики РУ
Математическое описание системы АРУ
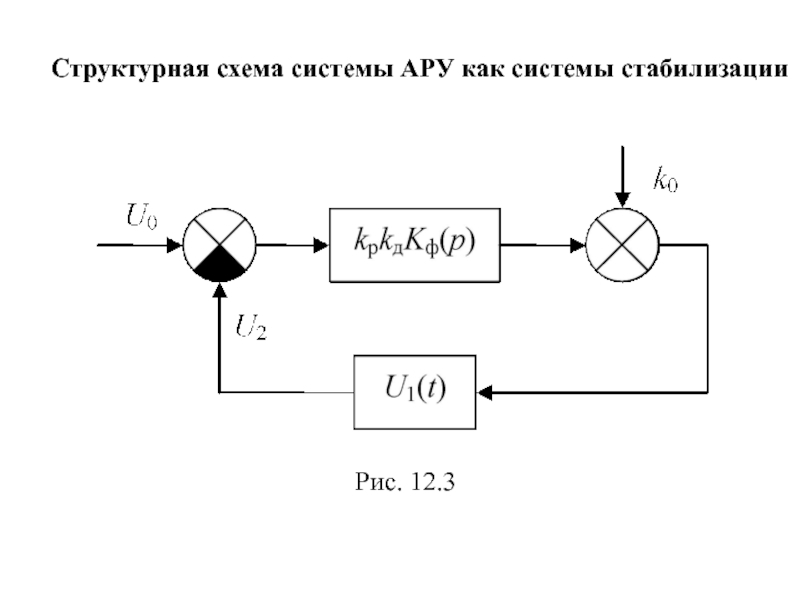
Структурная схема системы АРУ как системы стабилизации
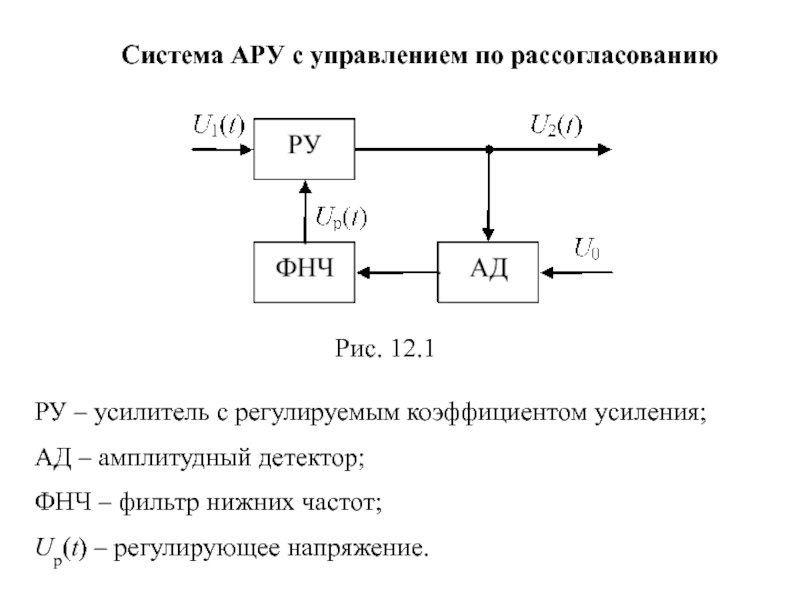
Слайд 82Система АРУ с управлением по рассогласованию
Рис. 12.1
РУ – усилитель с регулируемым
АД – амплитудный детектор;
ФНЧ – фильтр нижних частот;
Up(t) – регулирующее напряжение.
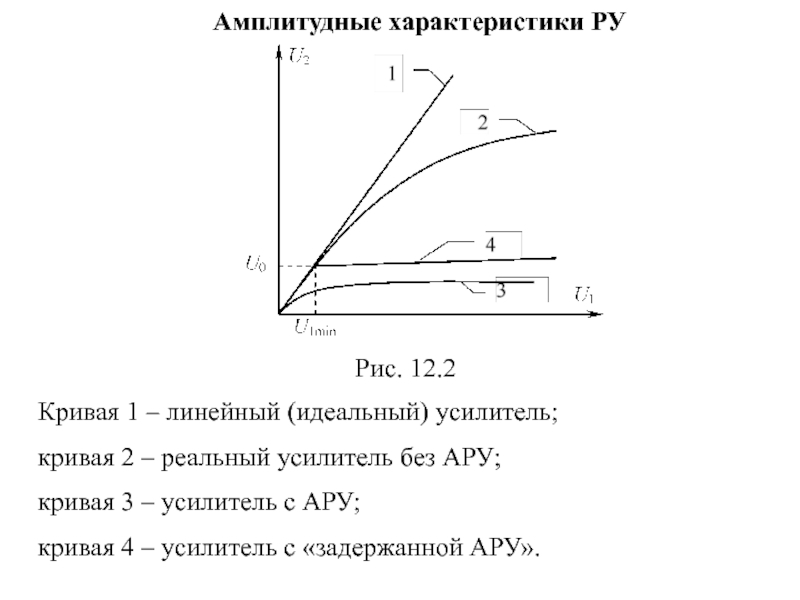
Слайд 83Амплитудные характеристики РУ
Рис. 12.2
Кривая 1 – линейный (идеальный) усилитель;
кривая 2 –
кривая 3 – усилитель с АРУ;
кривая 4 – усилитель с «задержанной АРУ».
Слайд 84Математическое описание системы АРУ
Амплитудная характеристика линейного усилителя:
U2(t)=kU1(t).
Регулировочная характеристика усилителя:
,
где
− крутизна регулировочной
− коэффициент усиления при разомкнутой цепи
обратной связи.
Слайд 85Характеристика АД при линейном детектировании:
где
Регулирующее напряжение связано с выходным напряжением детектора дифференциальным уравнением (в операторной форме)
Up(t)=Kф(р)Uд(t).
Общее уравнение системы АРУ для режима сильного сигнала, когда U2≥U0:
U2(t)=[k0+k0kд(U0 - U2)Kф(p)]U1(t).
Слайд 87
Тема 3: «Системы частотной автоподстройки (ЧАП)»
Содержание
Функциональная схема системы частотной автоподстройки
Принцип
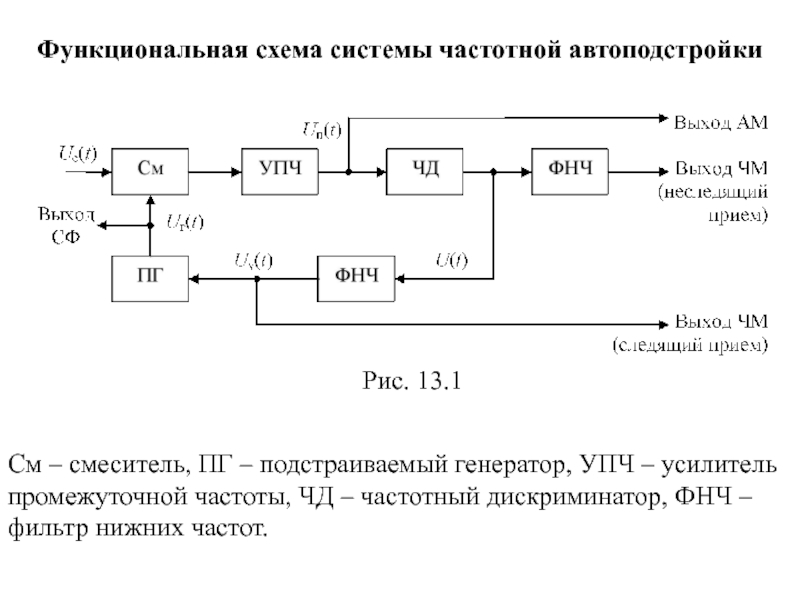
Слайд 88Функциональная схема системы частотной автоподстройки
Рис. 13.1
См – смеситель, ПГ –
Слайд 89Принцип действия системы ЧАП
Пример. Стабилизация промежуточной частоты супергетеродинного приемника
uc(t) – принятый
uг(t) – опорное колебание, вырабатываемое гетеродином;
fc0 – номинальная частота сигнала;
Δfc = fc – fc0;
fп = fc – fг;
Δf = fп – f0 – частотная расстройка.
Слайд 90
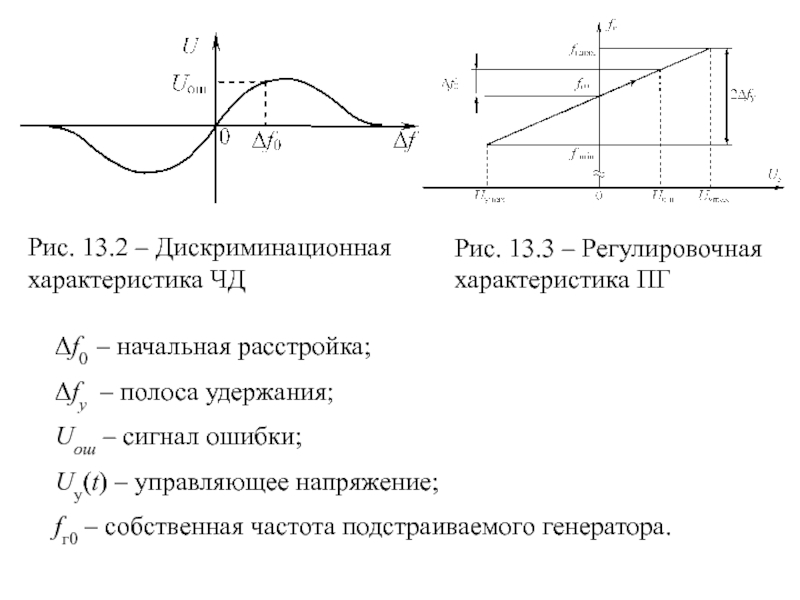
Рис. 13.2 – Дискриминационная характеристика ЧД
Рис. 13.3 – Регулировочная характеристика ПГ
Δf0
Δfу – полоса удержания;
Uош – сигнал ошибки;
Uу(t) – управляющее напряжение;
fг0 – собственная частота подстраиваемого генератора.
Слайд 91
Тема 4: «Системы фазовой автоподстройки (ФАП)»
Содержание
Применение системы ФАП
Функциональная схема
Дискриминационная характеристика фазового дискриминатора
Примеры использования системы ФАП
Слайд 92Применение системы ФАП
следящие фильтры доплеровских систем измерения скорости;
стабилизация промежуточной
синхронное детектирование сигналов;
демодуляторы ЧМ- и ФМ-сигналов;
синтезаторы частот;
следящие измерители координат (дальности, угла);
когерентное сложение сигналов в фазированных антенных
решётках.
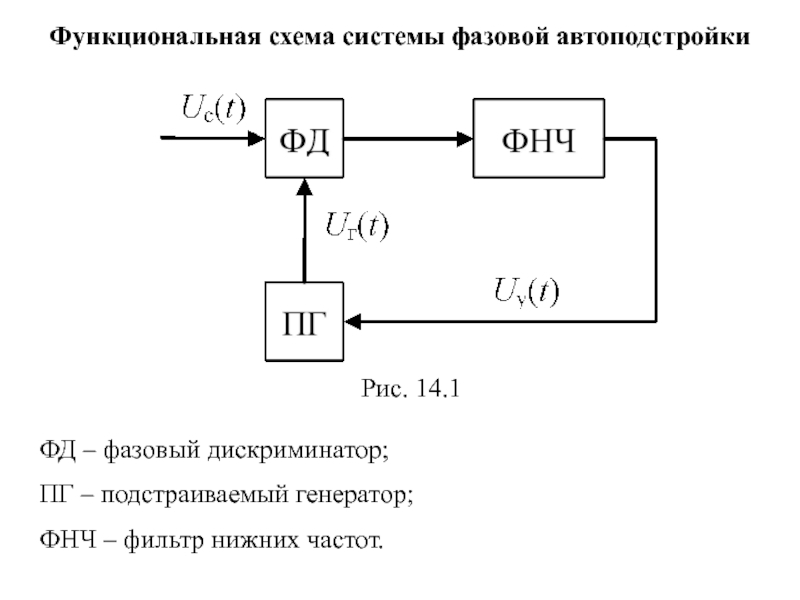
Слайд 93Функциональная схема системы фазовой автоподстройки
Рис. 14.1
ФД – фазовый дискриминатор;
ПГ – подстраиваемый
ФНЧ – фильтр нижних частот.
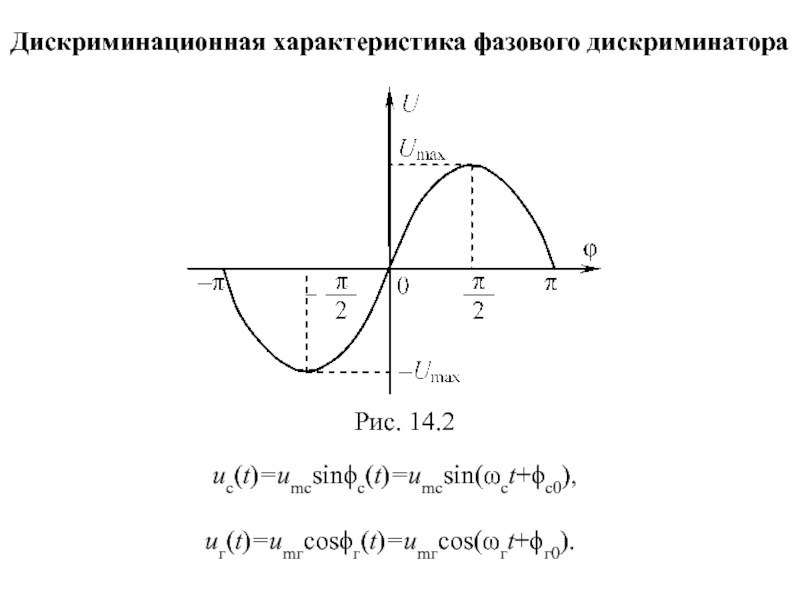
Слайд 94Дискриминационная характеристика фазового дискриминатора
uc(t)=umcsinϕc(t)=umcsin(ωct+ϕc0),
uг(t)=umгcosϕг(t)=umгcos(ωгt+ϕг0).
Рис. 14.2
Слайд 95
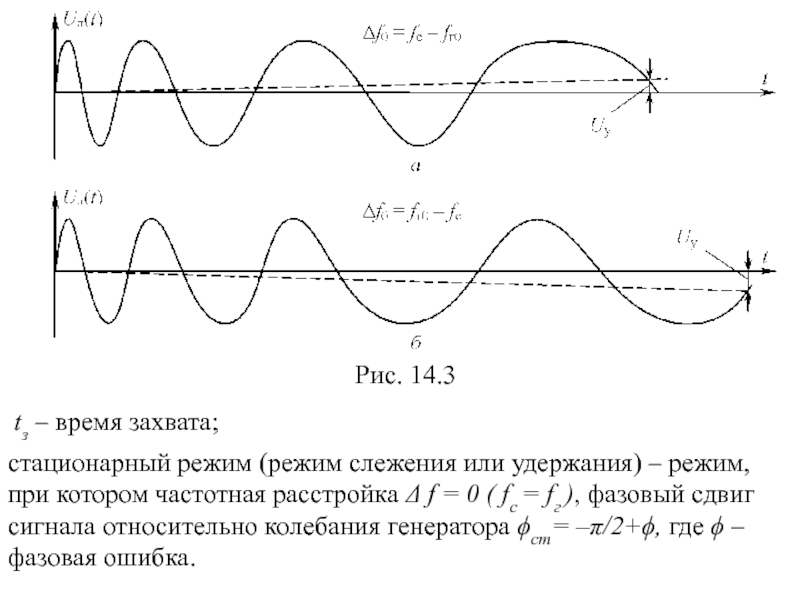
Рис. 14.3
tз – время захвата;
стационарный режим (режим слежения или удержания) –
Слайд 96
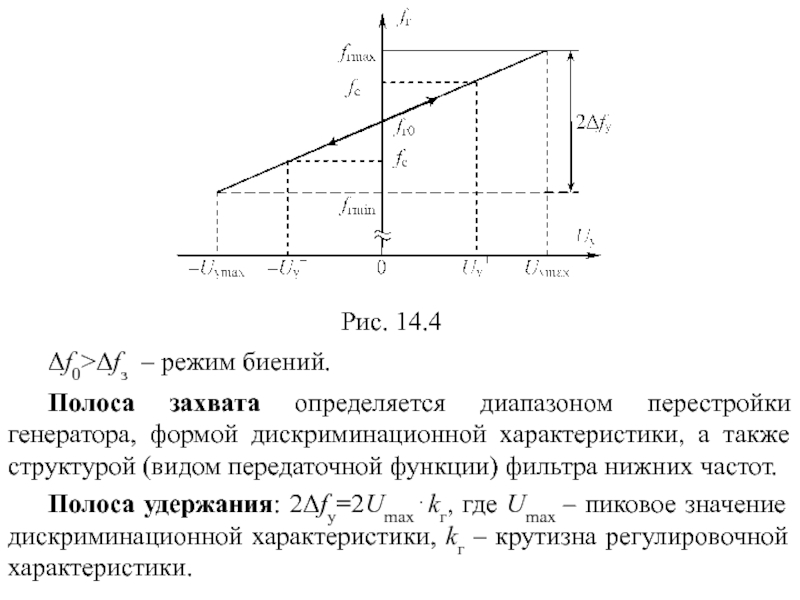
Рис. 14.4
Δf0>Δfз – режим биений.
Полоса захвата определяется диапазоном перестройки генератора, формой
Полоса удержания: 2Δfу=2Umax⋅kг, где Umax – пиковое значение дискриминационной характеристики, kг – крутизна регулировочной характеристики.
Слайд 98Примеры использования системы ФАП
Рис. 14.6 – Функциональная схема супергетеродинного приёмника
См –
Следящий фильтр на базе системы ФАП: выход фильтра – выход подстраиваемого генератора.
Слайд 99Линейная модель системы ФАП
Линейная аппроксимация дискриминационной характеристики:
U(ϕ)≅kдϕ (ϕ
K(p)=kг⋅KФ(p) – передаточная функция ФНЧ и ПГ;
ϕс и ϕг – фазовые сдвиги сигнала и колебания генератора, обусловленные отклонениями частот относительно номинального значения fс0 =fг0.
Рис. 14.7
Слайд 100
Тема 5: «Системы слежения за задержкой
сигнала (ССЗ)»
Содержание
Дискриминационная характеристика временного дискриминатора
Временной
Формирование дискриминационной характеристики
Структурная схема системы слежения за задержкой
Слайд 103Формирование дискриминационной характеристики
Рис. 15.3
U1, U2 – выходные напряжения каналов 1 и
– временное рассогласование.
Слайд 104Структурная схема системы слежения за задержкой
Временное рассогласование
Выходное напряжение дискриминатора
где
– полезная составляющая;
– помеха.
Зависимость управляющего напряжения
Uу(t)=Kф(p)Uд(t), (15.3)
где KФ(p) – передаточная функция ФНЧ.
Слайд 105Регулировочная характеристика схемы управляемой задержки
где
– значение задержки Uу=0,
– крутизна регулировочной характеристики
(коэффициент передачи СУЗ, имеющая размерность мкс/В.
Аппроксимиация зависимости U(Δτ) при малых рассогласованиях Δτ
где
Слайд 106
Рис. 15.4
Рис. 15.5
К(p)=kPKФ(p) – передаточная функция, описывающая схему управляемой задержки и
Линейная модель ССЗ позволяет решать задачи определения запаса устойчивости, быстродействия, точности.
Слайд 107
Тема 6: «Системы слежения за направлением прихода сигналов (ССН)»
Содержание
Амплитудный пеленгатор, использующий
Структурная схема ССН
Слайд 108Амплитудный пеленгатор, использующий суммарно-разностный метод пеленгования.
Рис. 16.1
О1 и О2 – облучатели;
Слайд 109
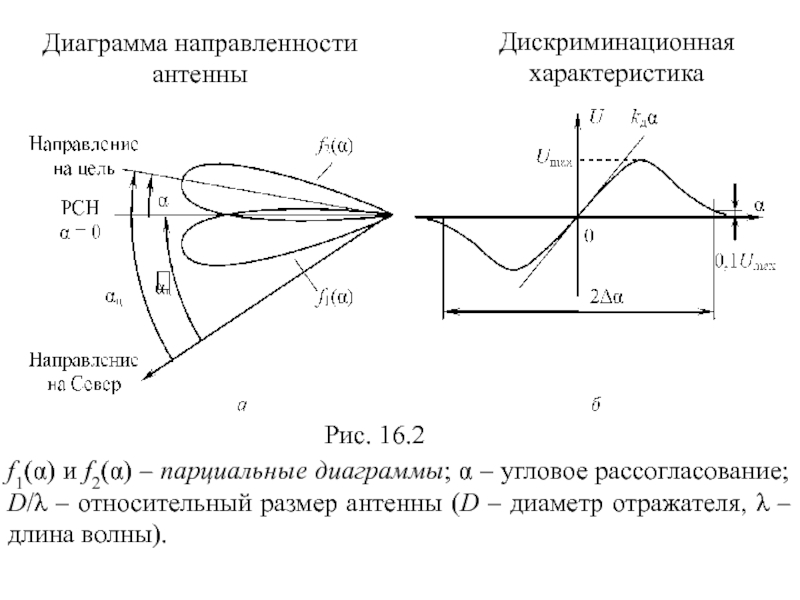
Диаграмма направленности
антенны
Дискриминационная характеристика
Рис. 16.2
f1(α) и f2(α) – парциальные диаграммы; α
Слайд 110Угловое рассогласование
где αц – азимут (пеленг) цели,
– оценка азимута.
Напряжение на
Uд(t)=U(α)+n(t,α), (16.2)
где U(α) –дискриминационная характеристика; n(t,α) – помеха.
U(α)=kфUpп(t,α)Ucп(t). (16.3)
U0 – амплитуда сигнала на выходе суммарного канала; Up(α) и Uc(α) – зависимости амплитуды сигнала на входе от α соответственно для разностного и суммарного каналов; fp(α)=f2(α) – f1(α) и fc(α)=f1(α)+f2(α).
Слайд 111Управляющее напряжение
Uу(t)=kуUд(t), (16.6)
где Ωд(t) – управляемая переменная (скорость вращения ротора двигателя);
где
где kP – коэффициент передачи редуктора (интегрирующего звена).














![Дифференциальное уравнение системыy(t) = K(p)[U(e)+ n(t, e)]. (4.2)Линеаризация](/img/tmb/2/196632/7635a3facf00986ec50abae6fda730b1-800x.jpg)