- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы логики (Решение заданий ЕГЭ и ОГЭ по информатике с использованием элементов алгебры логики) презентация
Содержание
- 1. Основы логики (Решение заданий ЕГЭ и ОГЭ по информатике с использованием элементов алгебры логики)
- 2. Этапы развития логики 1-й этап связан
- 3. 2-й этап – появление математической логики. Основы
- 4. Окончательно развил логику как науку англичанин Джордж
- 5. 1. Кто является основоположником формальной логики?
- 6. Задания 2 Значение логического выражения
- 7. Высказывание - это предложение на любом языке,
- 8. Высказывание - это предложение на любом языке,
- 9. Высказывание или нет? Зимой идет дождь. Снегири
- 10. Простые и сложные высказывания Высказывания бывают простые
- 11. Конъюнкция - логическая операция, ставящая в соответствие
- 12. Дизъюнкция - логическая операция, которая каждым двум
- 13. Инверсия - логическая операция, которая каждому
- 14. Для какого из приведённых значений числа X
- 15. Для какого из приведённых значений числа X
- 16. Для какого из приведённых значений числа X
- 17. Для какого из приведённых значений числа X
- 18. Для какого из приведённых чисел истинно высказывание:
- 19. Для какого из приведённых значений числа X
- 20. Для какого из приведённых чисел ложно высказывание: НЕ (ЧИСЛО
- 21. Для какого из приведённых имён истинно высказывание:
- 22. Для какого из приведённых имён ложно высказывание:
- 23. Задания 18 Осуществление поиска информации в Интернете
- 24. Использование метода кругов Эйлера для решения задач поиска информации
- 25. Круги Эйлера Круги Эйлера — геометрическая
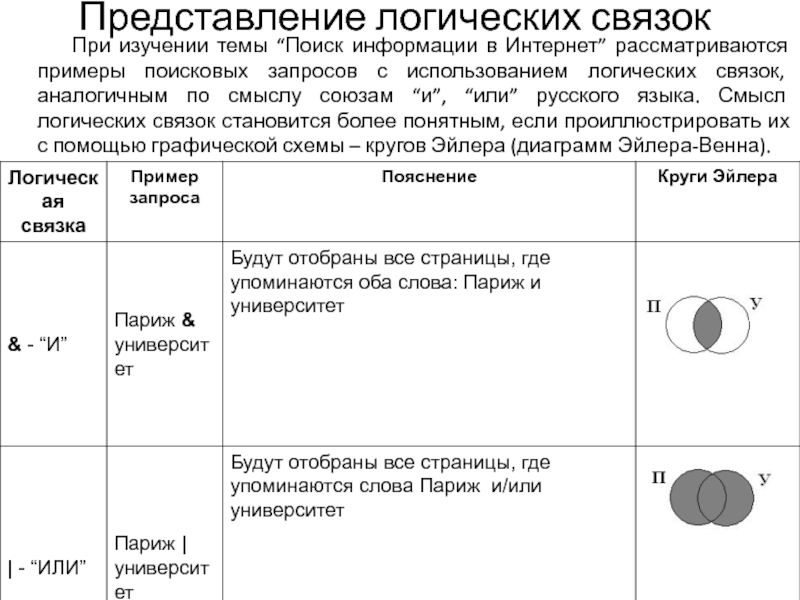
- 26. Представление логических связок
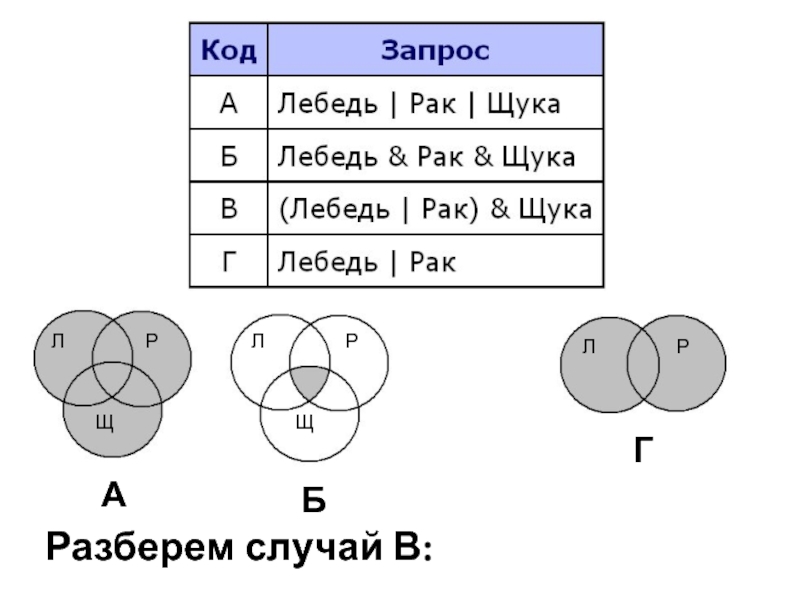
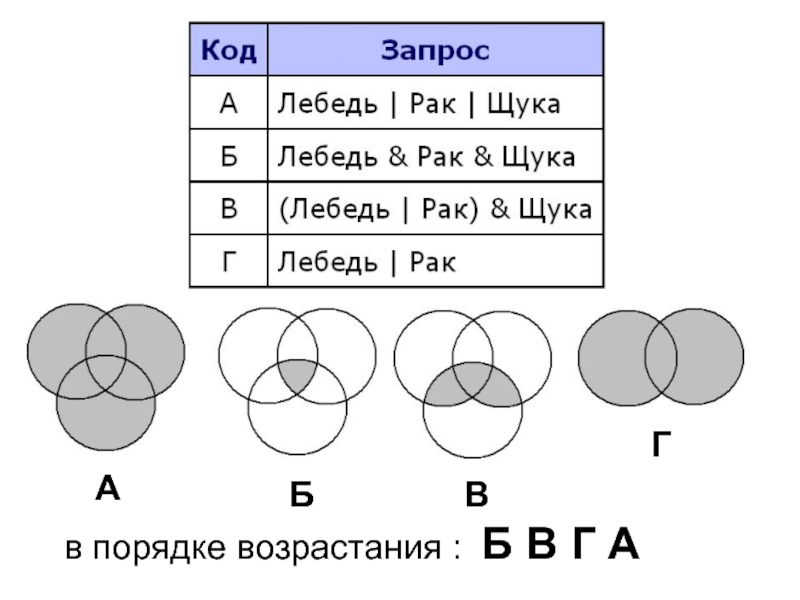
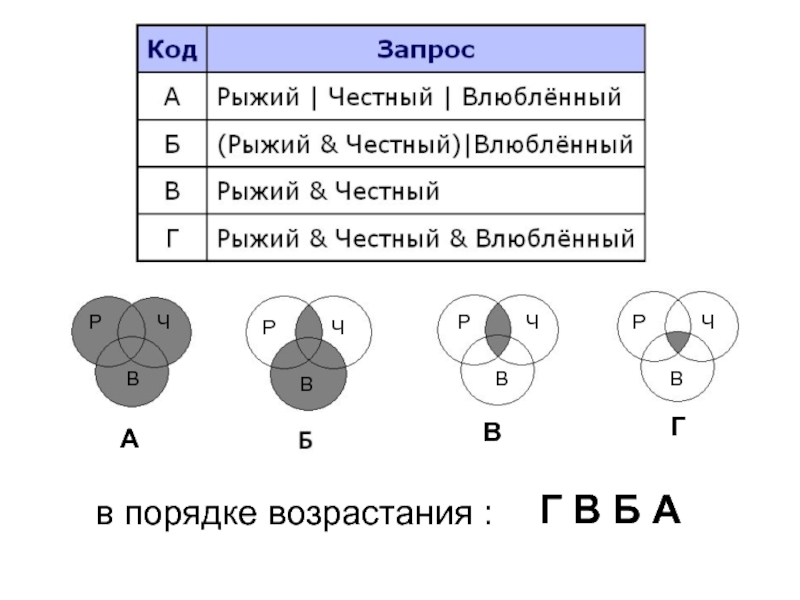
- 27. В таблице приведены запросы к поисковому
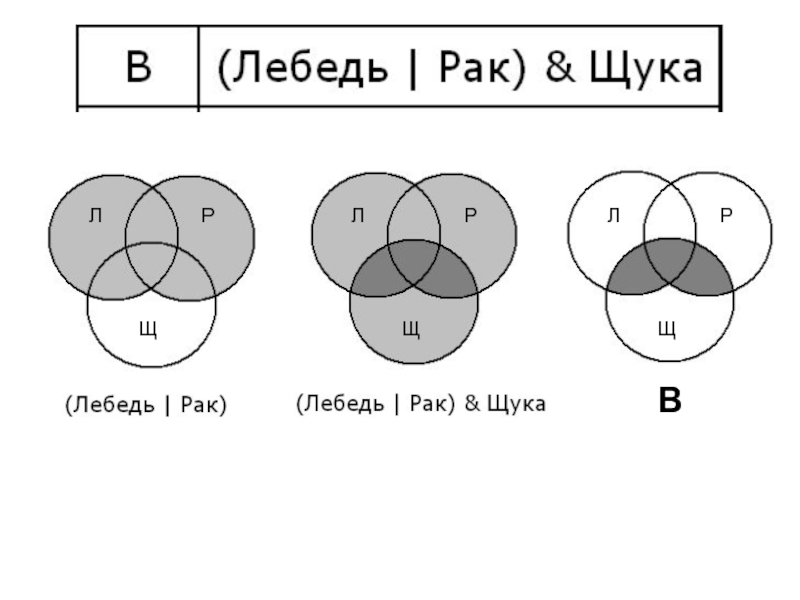
- 28. Разберем случай В:
- 30. в порядке возрастания : Б В Г А
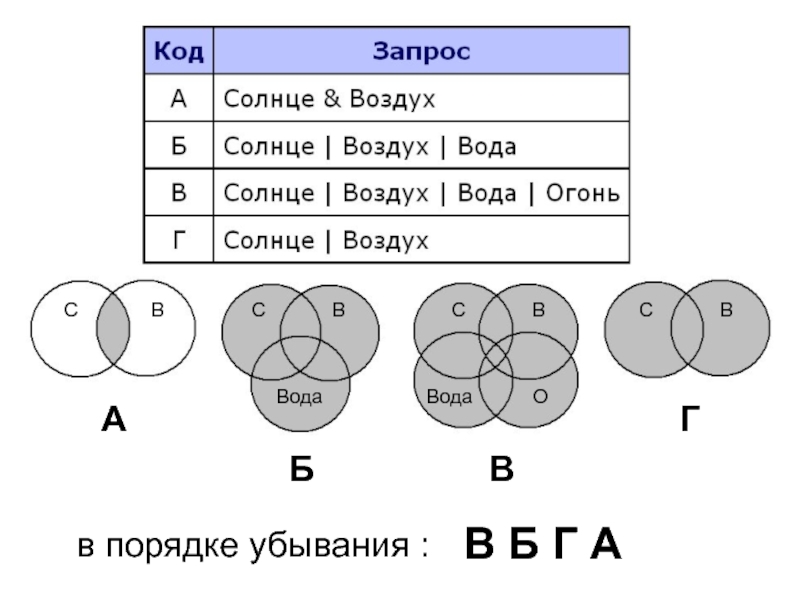
- 31. в порядке убывания : В Б Г А
- 32. в порядке возрастания : Г В Б А
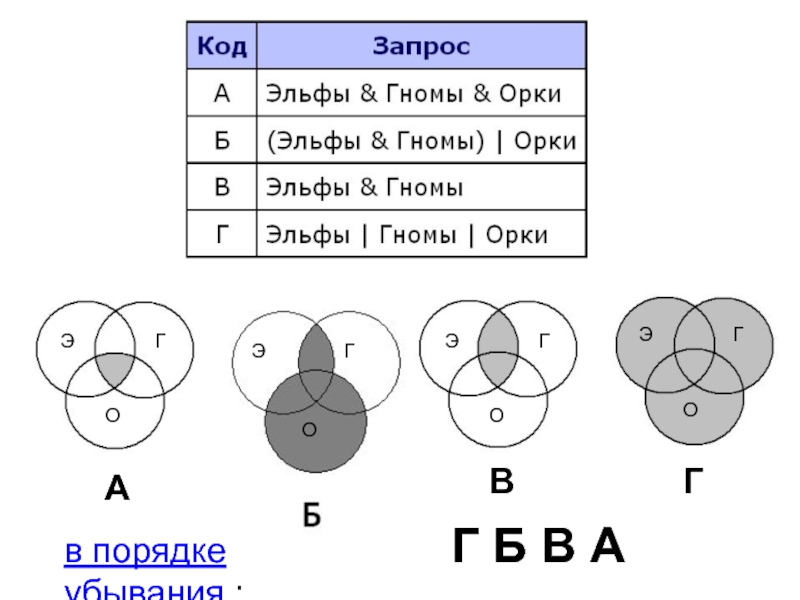
- 33. в порядке убывания : Г Б В А
- 34. Чем больше ИЛИ -
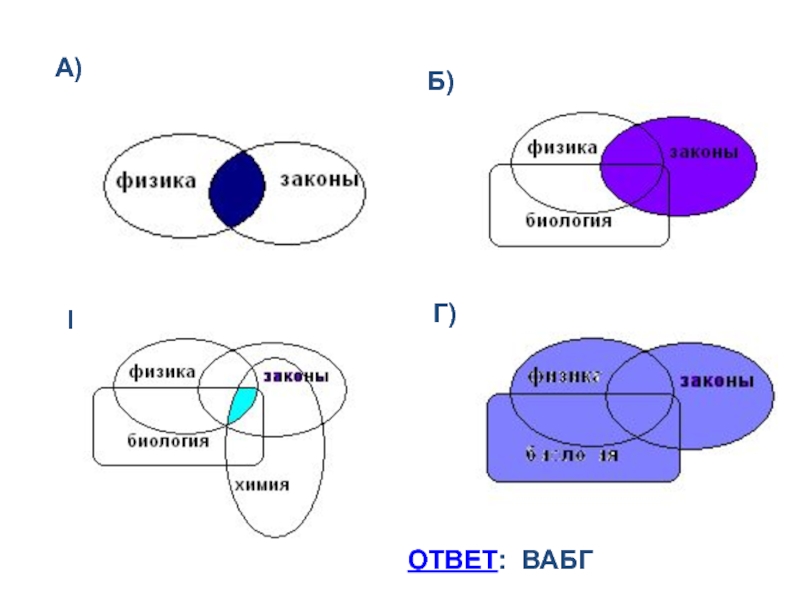
- 35. А) Б) Г) В) ОТВЕТ: ВАБГ
Слайд 1Тема урока:
Основы логики
(Решение заданий ЕГЭ и ОГЭ по информатике с использованием
Слайд 2Этапы развития логики
1-й этап связан с работами ученого и философа Аристотеля
Он подверг анализу человеческое мышление, его
формы – понятие, суждение, умозаключение.
Так возникла формальная логика.
Слайд 32-й этап – появление математической логики. Основы ее заложил немецкий ученый
считал, что можно заменить простые рассуждения действиями со знаками, и привел соответствующие правила.
Слайд 4Окончательно развил логику как науку англичанин Джордж Буль (1815-1864). Он является
В его работах логика обрела свой алфавит, свою орфографию и грамматику.
Недаром начальный раздел математической логики называют алгеброй логики, или булевой алгеброй.
Слайд 51. Кто является основоположником формальной логики?
Аристотель.
2. Кто является основоположником алгебры логики?
Джордж Буль
Слайд 7Высказывание - это предложение на любом языке, содержание которого можно однозначно
Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.
В алгебре логики высказывания обозначают буквами и называют логическими переменными.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.
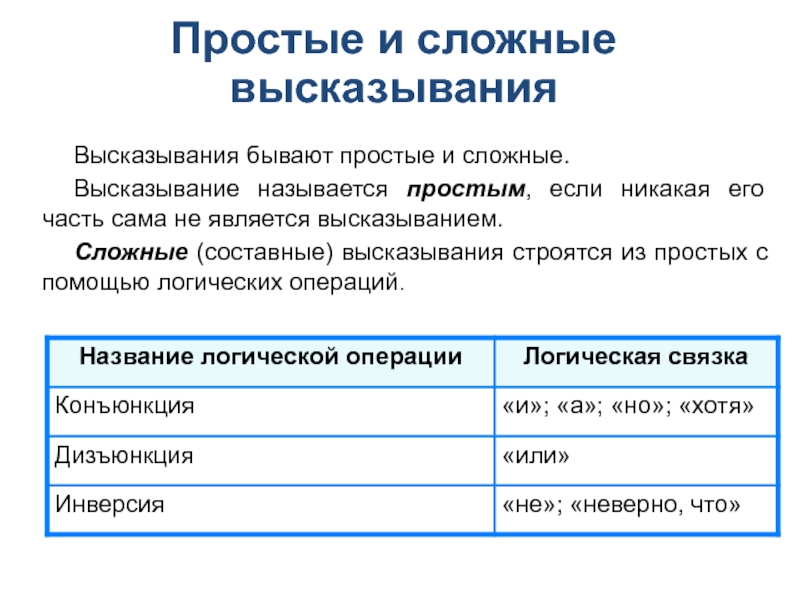
Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических операций
Слайд 8Высказывание - это предложение на любом языке, содержание которого можно однозначно
В русском языке высказывания выражаются повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва - столица.
Побудительные и вопросительные предложения высказываниями не являются.
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?
Высказывание
Но не всякое повествовательное предложение является высказыванием:
Это высказывание ложное.
Слайд 9Высказывание или нет?
Зимой идет дождь.
Снегири живут в Крыму.
Кто к нам пришел?
У
Как пройти в библиотеку?
Переведите число в десятичную систему.
Запишите домашнее задание
Слайд 10Простые и сложные высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым, если
Сложные (составные) высказывания строятся из простых с помощью логических операций.
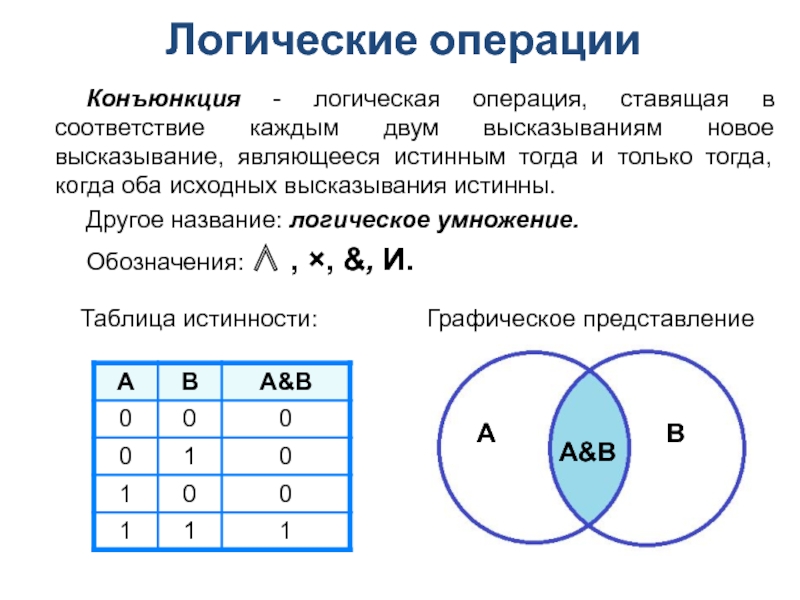
Слайд 11Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое
Другое название: логическое умножение.
Обозначения: ∧ , ×, &, И.
Логические операции
Таблица истинности:
Графическое представление
A
B
А&В
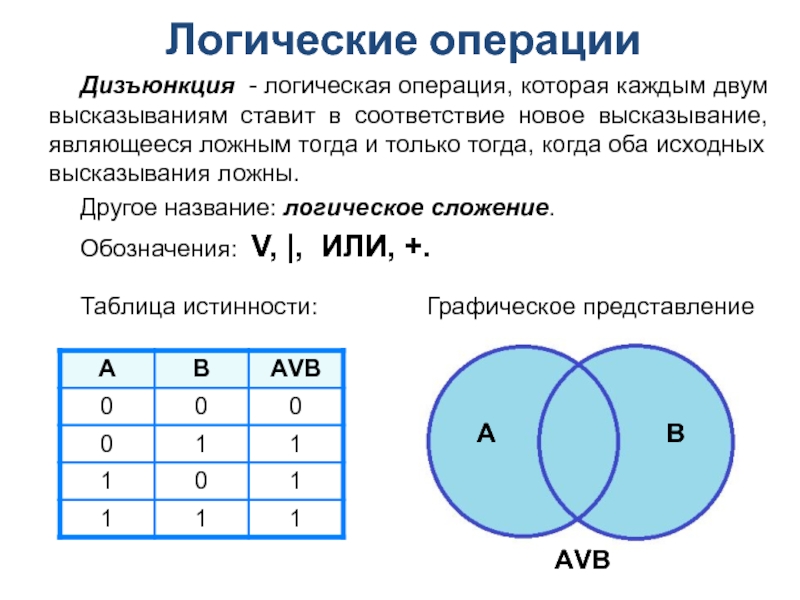
Слайд 12Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие
Другое название: логическое сложение.
Обозначения: V, |, ИЛИ, +.
Логические операции
Таблица истинности:
Графическое представление
A
B
АVВ
Слайд 13
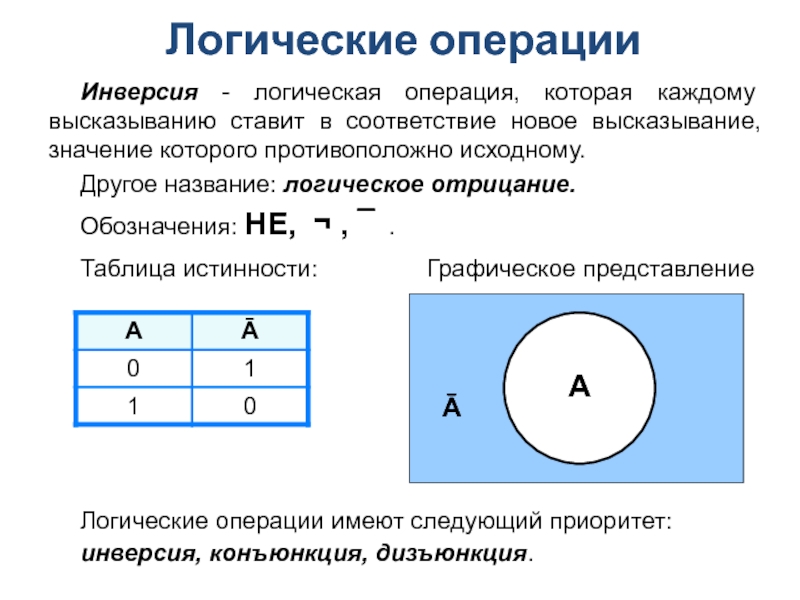
Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое
Другое название: логическое отрицание.
Обозначения: НЕ, ¬ , ¯ .
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.
Логические операции
Таблица истинности:
Графическое представление
A
Ā
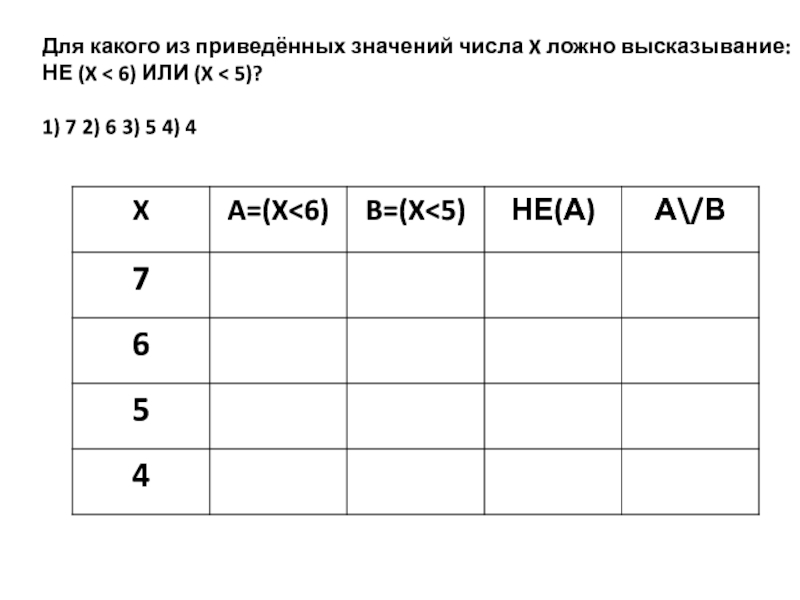
Слайд 14Для какого из приведённых значений числа X ложно высказывание:
НЕ (X
1) 7 2) 6 3) 5 4) 4
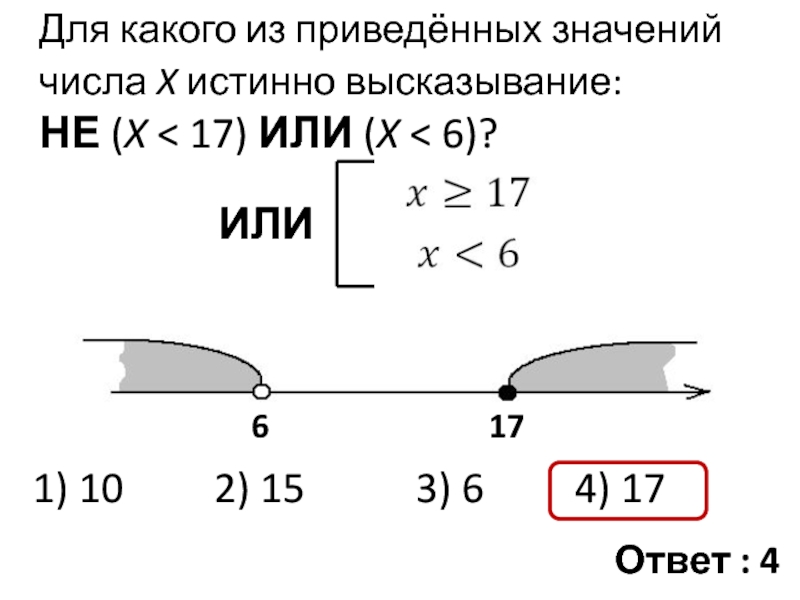
Слайд 15Для какого из приведённых значений числа X истинно высказывание: НЕ (X
ИЛИ
1) 10 2) 15 3) 6 4) 17
Ответ : 4
Слайд 16Для какого из приведённых значений числа X истинно высказывание:
(X
1) 9 2) 8 3) 7 4) 6
Слайд 17Для какого из приведённых значений числа X истинно высказывание:
НЕ(число
1) 24 2) 45 3) 74 4) 99
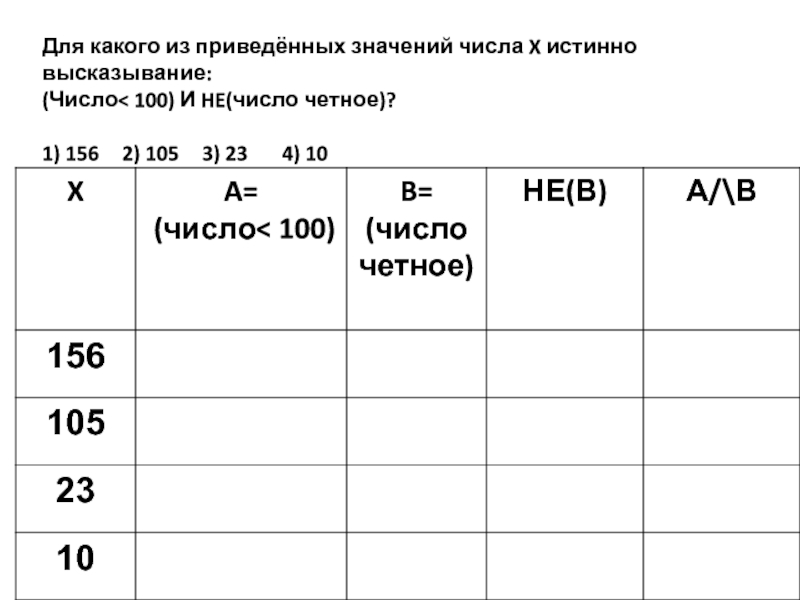
Слайд 18Для какого из приведённых чисел истинно высказывание:
(число < 100) И
1) 156 2) 105 3) 23 4) 10
число < 100
НЕ (число чётное)
И
Ответ : 3
Слайд 19Для какого из приведённых значений числа X истинно высказывание:
(Число< 100)
1) 156 2) 105 3) 23 4) 10
Слайд 20Для какого из приведённых чисел ложно высказывание:
НЕ (ЧИСЛО
1) 123 2) 56 3) 9 4) 8
Ответ : 4
Слайд 21Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква согласная)
Юлиан 2) Константин
3) Екатерина 4) Светлана
Ответ : 1
Слайд 22Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква согласная)
Егор 2) Тимур
3) Вера 4) Любовь
ь — согласная
Ответ : 3
Слайд 25 Круги Эйлера
Круги Эйлера — геометрическая схема, с помощью которой можно
Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все комбинаций свойств, то есть конечную булеву алгебру. При диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
При решении целого ряда задач Леонард Эйлер использовал идею
изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и
математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.