- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сети Петри презентация
Содержание
- 1. Сети Петри
- 2. Дискретные динамические системы Одним из наиболее общих
- 3. Детерминированные последовательные системы Понятие конечного автомата существенно
- 4. Недетерминированные параллельные системы Подобные системы состоят из
- 5. Модели дискретных систем При моделировании дискретных систем
- 6. Синхронные модели В синхронных моделях события явно
- 7. Асинхронные модели В моделях этого типа вышеперечисленные
- 8. Условия Причинно-следственные связи между событиями в асинхронных
- 9. Карл Адам Петри Сетевая асинхронная модель для
- 10. Ёмкость условия В модели Петри условия принято
- 11. Теоретико-множественное определение сетей Петри Введем понятие мультимножества,
- 12. Определения Множество позиций: P = {p1, p2,
- 13. Определения Использование мультимножеств входных и выходных позиций
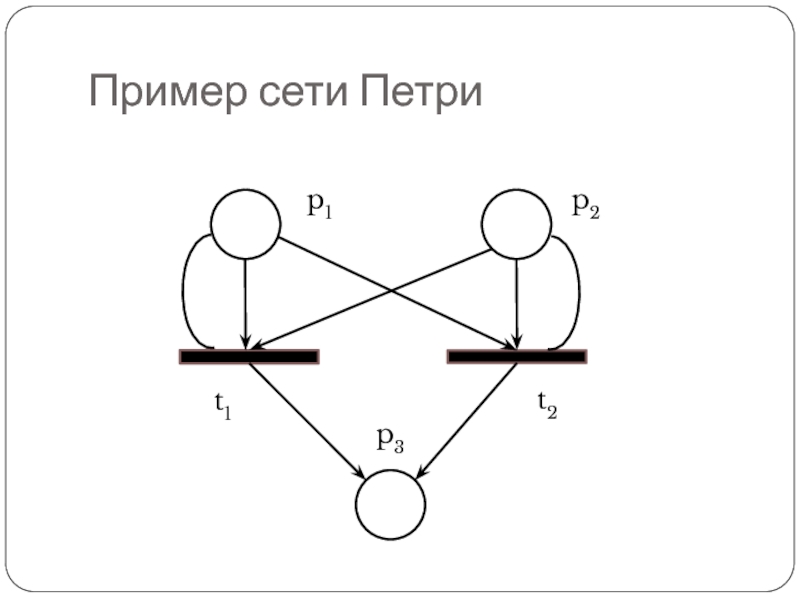
- 14. Пример сети Петри P = {p1, p2,
- 15. Графы сетей Петри Наглядным представлением сети Петри
- 16. Пример сети Петри p1 p3 p2 t1 t2
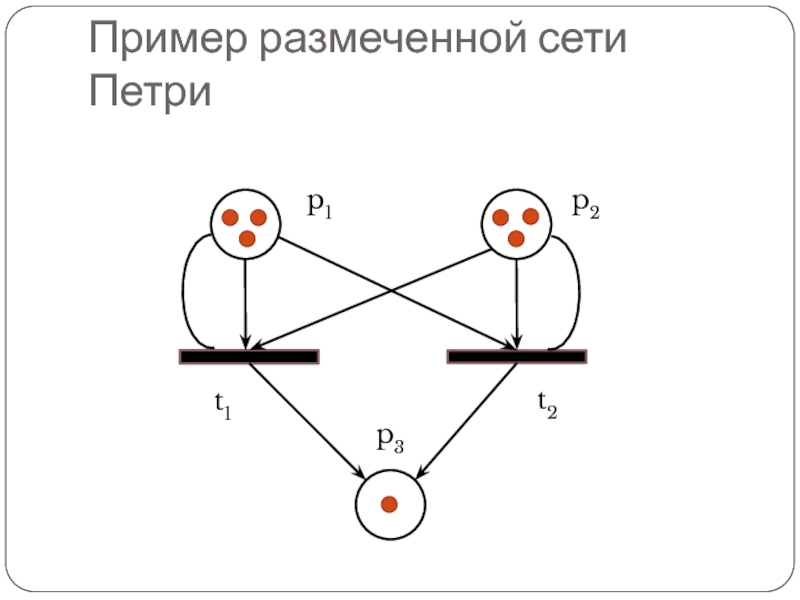
- 17. Разметка сетей Петри В сетях Петри выполнение
- 18. Разметка сетей Петри
- 19. Пример размеченной сети Петри
- 20. Работа сети Петри Работу сети можно представить
- 21. Функции переходов
- 22. Условие срабатывания перехода
- 23. Работа сети Если два или более перехода
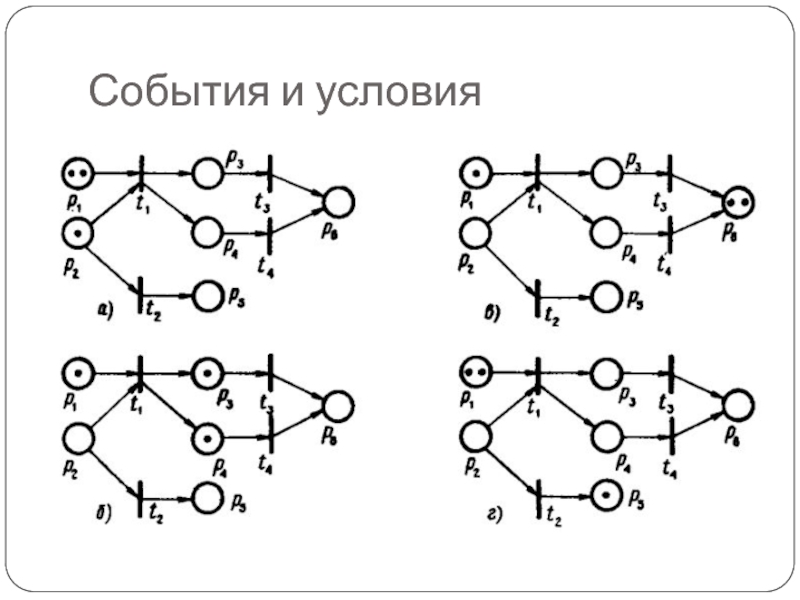
- 24. События и условия
- 25. Условие завершения работы сети Сеть останавливается,
- 26. Моделирование взаимодействия процессов Далее будем рассматривать параллельные
- 27. Задача о взаимном исключении Пусть несколько процессов
- 28. Критическая секция Критическая секция – это
- 29. Моделирование взаимного исключения
- 30. Задача о производителе/потребителе В задаче о производителе/потребителе
- 31. Моделирование буфера обмена
- 32. Задача об обедающих философах В некоем пансионе
- 33. Проблема тупика В задаче об обедающих философах
- 34. Решение проблемы тупика Проблема тупика в этой
- 35. Моделирование разрешения тупиковой ситуации
- 36. Свойства сетей Петри.Ограниченность Позиция p∈P сети Петри
Слайд 2Дискретные динамические системы
Одним из наиболее общих понятий в кибернетике и информатике
является понятие дискретной динамической системы
Дискретной динамической системой называется система обладающая некоторым набором состояний, переход между которыми происходит в дискретные моменты времени
Примером дискретной динамической системы является автомат
Дискретной динамической системой называется система обладающая некоторым набором состояний, переход между которыми происходит в дискретные моменты времени
Примером дискретной динамической системы является автомат
Слайд 3Детерминированные последовательные системы
Понятие конечного автомата существенно связано с понятиями алгоритма и
последовательной алгоритмической системы
Поведение таких систем детерминировано: они последовательно переходят из одного состояния в другое в соответствии в определенной функцией перехода
Конечные автоматы не подходят для описания дискретных систем более общего вида – недетерминированных параллельных систем
Поведение таких систем детерминировано: они последовательно переходят из одного состояния в другое в соответствии в определенной функцией перехода
Конечные автоматы не подходят для описания дискретных систем более общего вида – недетерминированных параллельных систем
Слайд 4Недетерминированные параллельные системы
Подобные системы состоят из отдельных компонентов, функционирующих параллельно и
взаимодействующих между собой асинхронно (т.е. в произвольные моменты времени)
Примерами таких систем могут служить:
вычислительные системы, в том числе и параллельные;
компьютерные сети и программные системы, обеспечивающие их функционирование;
экономические системы;
системы управления дорожным движением и т. д.
Примерами таких систем могут служить:
вычислительные системы, в том числе и параллельные;
компьютерные сети и программные системы, обеспечивающие их функционирование;
экономические системы;
системы управления дорожным движением и т. д.
Слайд 5Модели дискретных систем
При моделировании дискретных систем действия их компонентов представляются абстрактными
событиями
Примеры событий:
выполнение оператора программы,
прерывание в операционной системе,
завершение технологической операции в производственном процессе и т.д.
Событие может произойти один раз или повторяться многократно; совокупность событий в динамической системе, образует процесс, порождаемый этой системой
Примеры событий:
выполнение оператора программы,
прерывание в операционной системе,
завершение технологической операции в производственном процессе и т.д.
Событие может произойти один раз или повторяться многократно; совокупность событий в динамической системе, образует процесс, порождаемый этой системой
Слайд 6Синхронные модели
В синхронных моделях события явно привязаны к определенным моментам или
интервалам времени
Это приводит к необходимости учета состояния всех компонентов системы при смене её общего состояния
В синхронных моделях не заложена информация о причинно-следственных связях между событиями в системе
Они сложны для моделирования длительных событий
Это приводит к необходимости учета состояния всех компонентов системы при смене её общего состояния
В синхронных моделях не заложена информация о причинно-следственных связях между событиями в системе
Они сложны для моделирования длительных событий
Слайд 7Асинхронные модели
В моделях этого типа вышеперечисленные проблемы отсутствуют
В асинхронных моделях временная
связь заменяется причинно-следственной
Отказ от времени позволяет считать события или неделимыми («мгновенными»), или составными, состоящими из «подсобытий»
Отказ от времени позволяет считать события или неделимыми («мгновенными»), или составными, состоящими из «подсобытий»
Слайд 8Условия
Причинно-следственные связи между событиями в асинхронных моделях можно реализовать указанием условий,
при которых то или иное событие может реализоваться
Примеры условий:
наличие данных для выполнения некоторой операции в программе,
наличие деталей на конвейере,
появление сигнала на входе устройства управления
Примером асинхронных моделей являются сети Петри
Примеры условий:
наличие данных для выполнения некоторой операции в программе,
наличие деталей на конвейере,
появление сигнала на входе устройства управления
Примером асинхронных моделей являются сети Петри
Слайд 9Карл Адам Петри
Сетевая асинхронная модель для недетерминированных систем была предложена в
60-х годах прошлого века немецким математиком Карлом Адамом Петри
Слайд 10Ёмкость условия
В модели Петри условия принято характеризовать ёмкостью
Предполагается, что условие может
быть:
не выполнено – ёмкость 0,
выполнено – ёмкость 1,
Выполнено с n-кратным запасом – ёмкость n
В терминах сетей Петри события называются переходами, а условия – позициями
Предусловия реализации события – это входные позиции для перехода, а постусловия – выходные позиции
не выполнено – ёмкость 0,
выполнено – ёмкость 1,
Выполнено с n-кратным запасом – ёмкость n
В терминах сетей Петри события называются переходами, а условия – позициями
Предусловия реализации события – это входные позиции для перехода, а постусловия – выходные позиции
Слайд 11Теоретико-множественное определение сетей Петри
Введем понятие мультимножества, как множества, допускающего вхождение нескольких
экземпляров одного и того же элемента
Сеть Петри S является четверкой
S = (P, T, I, O), где
P – конечное множество позиций;
T – конечное множество переходов;
I – входная функция, сопоставляющая переходу мультимножество его входных позиций;
O – входная функция, сопоставляющая переходу мультимножество его входных позиций
Сеть Петри S является четверкой
S = (P, T, I, O), где
P – конечное множество позиций;
T – конечное множество переходов;
I – входная функция, сопоставляющая переходу мультимножество его входных позиций;
O – входная функция, сопоставляющая переходу мультимножество его входных позиций
Слайд 12Определения
Множество позиций:
P = {p1, p2, …, pn}, n ≥ 0;
Множество переходов:
T
= {t1, t2, …, tm}, m ≥ 0;
Входная функция:
I: T → P*, где P*- мультимножество входных позиций;
Выходная функция:
O: T → P*, где P*- мультимножество выходных позиций;
Входная функция:
I: T → P*, где P*- мультимножество входных позиций;
Выходная функция:
O: T → P*, где P*- мультимножество выходных позиций;
Слайд 13Определения
Использование мультимножеств входных и выходных позиций перехода, а не множеств, позволяет
позиции быть кратным входом и кратным выходом перехода соответственно
При этом кратность определяется числом экземпляров позиции в соответствующем мультимножестве.
Структура сети Петри определяется ее позициями, переходами, входной и выходной функциями
При этом кратность определяется числом экземпляров позиции в соответствующем мультимножестве.
Структура сети Петри определяется ее позициями, переходами, входной и выходной функциями
Слайд 14Пример сети Петри
P = {p1, p2, p3},
T = {t1, t2},
I(t1) =
{p1, p1, p2},
O(t1) = {p3},
I(t2) = {p1, p2, p2},
O(t2) = {p3}
O(t1) = {p3},
I(t2) = {p1, p2, p2},
O(t2) = {p3}
Слайд 15Графы сетей Петри
Наглядным представлением сети Петри является её графическое представление в
виде двудольного, ориентированного мультиграфа
Граф сети Петри обладает двумя типами узлов:
круг , представляющий позицию сети Петри,
планка, представляющая переход сети Петри
Ориентированные дуги этого графа соединяют переход с его входными и выходными позициями
Дуги направлены от входных позиций к переходу и от перехода к выходным позициям
В графе сети Петри невозможны дуги между двумя позициями и между двумя переходами (двудольность)
Граф сети Петри обладает двумя типами узлов:
круг , представляющий позицию сети Петри,
планка, представляющая переход сети Петри
Ориентированные дуги этого графа соединяют переход с его входными и выходными позициями
Дуги направлены от входных позиций к переходу и от перехода к выходным позициям
В графе сети Петри невозможны дуги между двумя позициями и между двумя переходами (двудольность)
Слайд 17Разметка сетей Петри
В сетях Петри выполнение условий изображается разметкой соответствующей позиции
путем размещения в ней числа фишек, соответствующего ёмкости этой позиции
Фишки изображаются на графе точками; количество фишек в позиции в процессе работы сети Петри может изменяться от 0 до бесконечности
Разметка μ сети Петри – это функция, отображающая множество позиций P во множество натуральных чисел N
μ: P → N
Фишки изображаются на графе точками; количество фишек в позиции в процессе работы сети Петри может изменяться от 0 до бесконечности
Разметка μ сети Петри – это функция, отображающая множество позиций P во множество натуральных чисел N
μ: P → N
Слайд 20Работа сети Петри
Работу сети можно представить как совокупность локальных действий, которые
называются срабатыванием переходов
Срабатывания соответствуют реализациям событий и приводят к локальному изменению условий, т.е. к изменению разметки сети
Переход может сработать (быть разрешенным) только в том случае, если выполняется его условие
Определим формально условие срабатывания перехода
Срабатывания соответствуют реализациям событий и приводят к локальному изменению условий, т.е. к изменению разметки сети
Переход может сработать (быть разрешенным) только в том случае, если выполняется его условие
Определим формально условие срабатывания перехода
Слайд 23Работа сети
Если два или более перехода не имеют общих входных мест,
то их срабатывания являются независимыми действиями и могут осуществляться в любой последовательности, либо параллельно
Если несколько переходов имеют общее входное место, то сработать может только один из них
Выбор срабатывающего перехода лежит за пределами формализма сети, что позволяет моделировать недетерминированные процессы
Если несколько переходов имеют общее входное место, то сработать может только один из них
Выбор срабатывающего перехода лежит за пределами формализма сети, что позволяет моделировать недетерминированные процессы
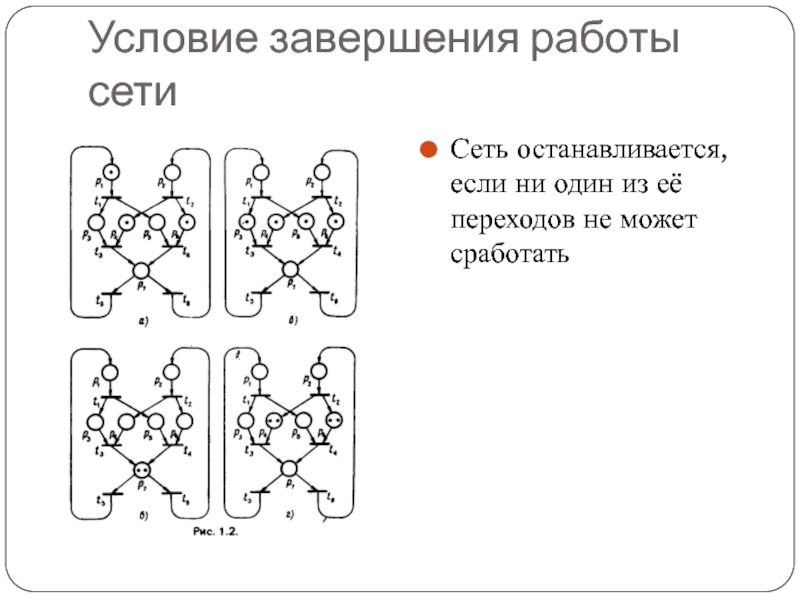
Слайд 25Условие завершения работы сети
Сеть останавливается, если ни один из её переходов
не может сработать
Слайд 26Моделирование взаимодействия процессов
Далее будем рассматривать параллельные системы процессов, допускающие взаимодействие процессов
во время их параллельного выполнения
Существуют различные виды взаимодействия (синхронизации) процессов, в том числе: взаимодействие посредством общей памяти; посредством передачи сообщения различных видов
Необходимо уметь моделировать различные механизмы синхронизации процессов
Существуют различные виды взаимодействия (синхронизации) процессов, в том числе: взаимодействие посредством общей памяти; посредством передачи сообщения различных видов
Необходимо уметь моделировать различные механизмы синхронизации процессов
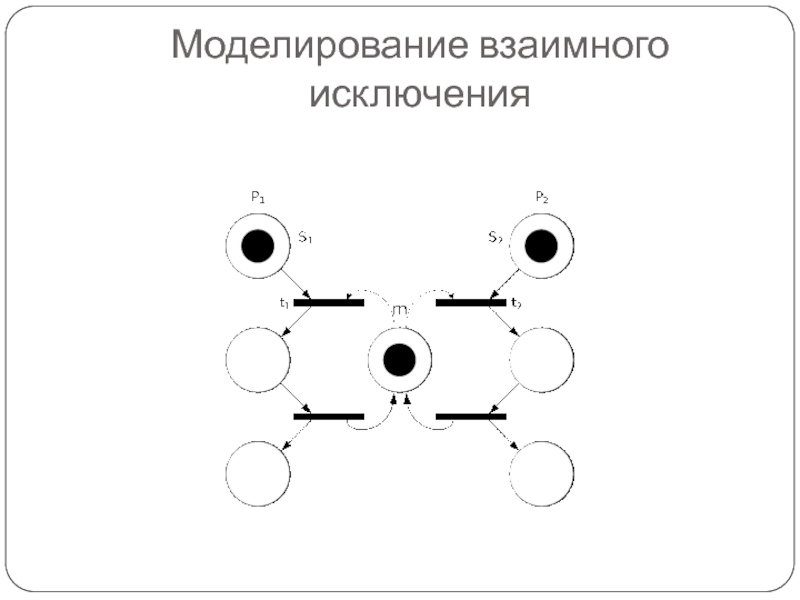
Слайд 27Задача о взаимном исключении
Пусть несколько процессов разделяют общую переменную, запись, файл
или другой элемент данных
Если два процесса и в одно и то же время пытаются изменить этот элемент данных, то могут возникнуть нежелательные искажения
Для решения подобных проблем используется метод взаимного исключения, основанный на понятии критическая секция.
Если два процесса и в одно и то же время пытаются изменить этот элемент данных, то могут возникнуть нежелательные искажения
Для решения подобных проблем используется метод взаимного исключения, основанный на понятии критическая секция.
Слайд 28Критическая секция
Критическая секция – это участок кода процесса, на котором
он осуществляет доступ к разделяемому объекту данных
Прежде, чем выполнить свою критическую секцию, процесс ждёт, пока другой процесс не закончит выполнение собственной критической секции и лишь затем он входит в критическую секцию
При этом блокируется доступ для любого другого процесса к своей критической секции до выхода этого процесса из критической секции
Прежде, чем выполнить свою критическую секцию, процесс ждёт, пока другой процесс не закончит выполнение собственной критической секции и лишь затем он входит в критическую секцию
При этом блокируется доступ для любого другого процесса к своей критической секции до выхода этого процесса из критической секции
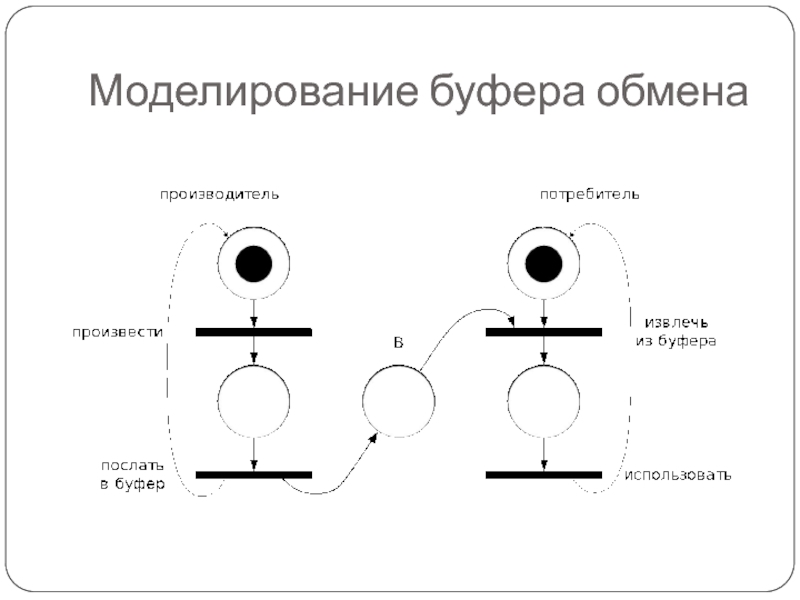
Слайд 30Задача о производителе/потребителе
В задаче о производителе/потребителе также присутствует разделяемый объект –
буфер, посредством которого реализуется взаимодействие через асинхронную передачу сообщений
Процесс-производитель создает сообщения, которые помещаются в буфер
Процесс-потребитель ждет, пока сообщение не будет помещено в буфер, извлекает его оттуда и использует
Процесс-производитель создает сообщения, которые помещаются в буфер
Процесс-потребитель ждет, пока сообщение не будет помещено в буфер, извлекает его оттуда и использует
Слайд 32Задача об обедающих философах
В некоем пансионе нашли пристанище пять философов. У
каждого философа была своя комната. Была у них и общая столовая с круглым столом, вокруг которого стояли пять стульев.
В центре стола стояла большая миска спагетти, содержимое которой постоянно пополнялось. На столе также лежало пять вилок, по одной между соседними посадочными местами.
Звали философов и за столом они располагались в этом же порядке, против часовой стрелки. Почувствовав голод, философ шёл в столовую, садился на свой стул, брал сначала слева от себя вилку, затем справа и приступал к еде. Закончив трапезу, он клал на место обе вилки, выходил из-за стола, и уходили размышлять
В центре стола стояла большая миска спагетти, содержимое которой постоянно пополнялось. На столе также лежало пять вилок, по одной между соседними посадочными местами.
Звали философов и за столом они располагались в этом же порядке, против часовой стрелки. Почувствовав голод, философ шёл в столовую, садился на свой стул, брал сначала слева от себя вилку, затем справа и приступал к еде. Закончив трапезу, он клал на место обе вилки, выходил из-за стола, и уходили размышлять
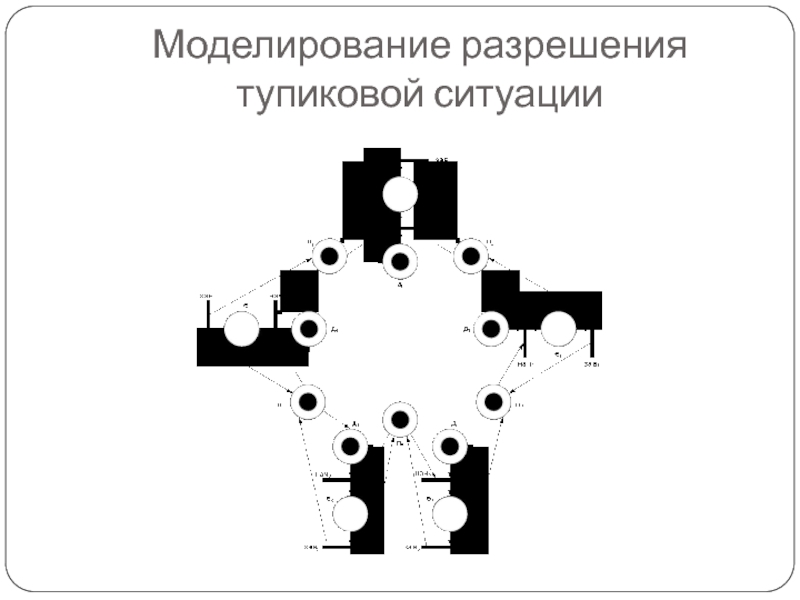
Слайд 33Проблема тупика
В задаче об обедающих философах возможна ситуация, в которой каждый
философ возьмет вилку слева, а затем будет ждать, когда освободится вилка с правой стороны
Так они будут ждать, пока не умрут от голода
Тем самым, это состояние системы «обедающие философы» является тупиковым
Так они будут ждать, пока не умрут от голода
Тем самым, это состояние системы «обедающие философы» является тупиковым
Слайд 34Решение проблемы тупика
Проблема тупика в этой системе может быть решена путем
следующей модификации ее правил поведения
Пусть философ при переходе из состояния размышления в состояние приема пищи берет одновременно обе вилки (слева и справа), если они свободны
Пусть философ при переходе из состояния размышления в состояние приема пищи берет одновременно обе вилки (слева и справа), если они свободны
Слайд 36Свойства сетей Петри.Ограниченность
Позиция p∈P сети Петри c начальной разметкой μ является
k-ограниченной, если μ`(p) ≤ k для любой достижимой разметки μ`.
Позиция называется ограниченной, если она является -ограниченной для некоторого целого значения .
Сеть Петри ограниченна, если все ее позиции ограниченны.
Позиция называется ограниченной, если она является -ограниченной для некоторого целого значения .
Сеть Петри ограниченна, если все ее позиции ограниченны.