- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сбалансированные деревья поиска презентация
Содержание
- 1. Сбалансированные деревья поиска
- 2. Пример: Необходимо расположить все слова некоторого текста
- 3. Допустим задан текст «Сэр Исаак Ньютон по
- 4. Текст в алфавитном порядке: ведет гравитация
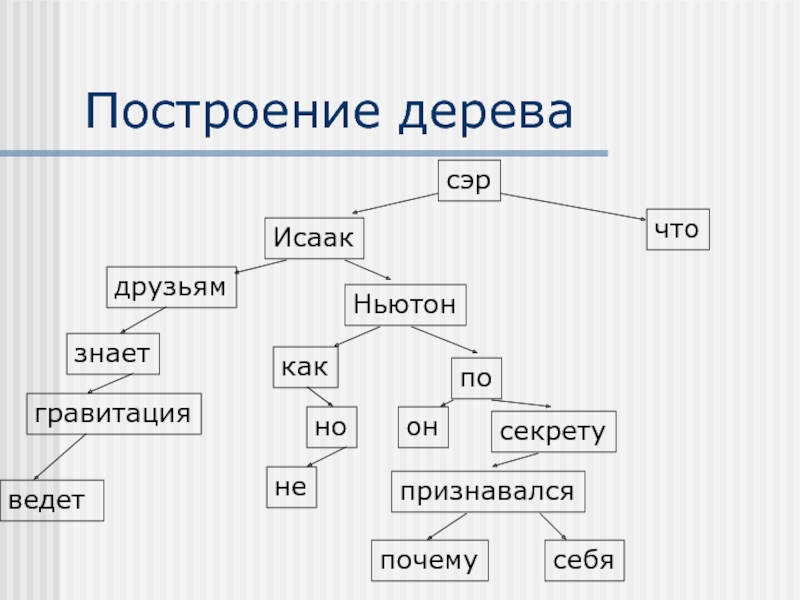
- 5. Построение дерева сэр
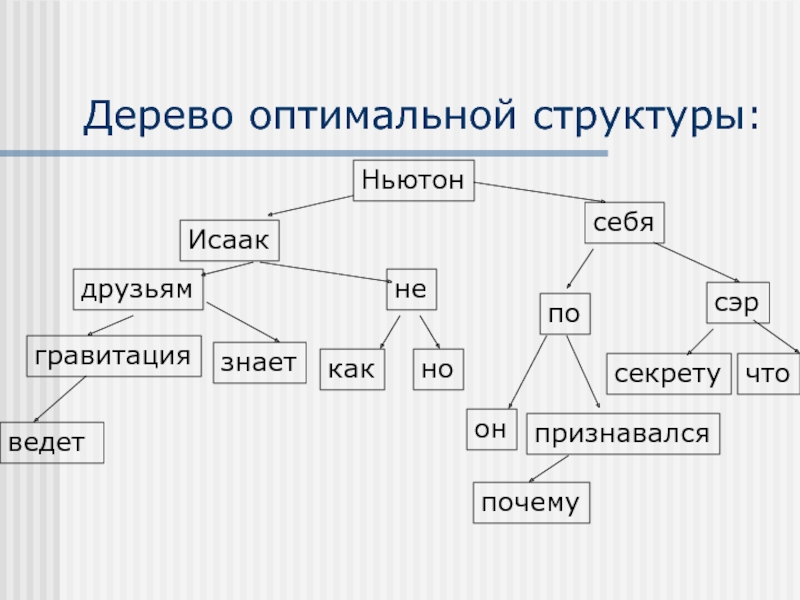
- 6. Дерево оптимальной структуры: Ньютон
- 7. Высота бинарного дерева Пусть бинарное дерево
- 8. Дерево максимальной высоты
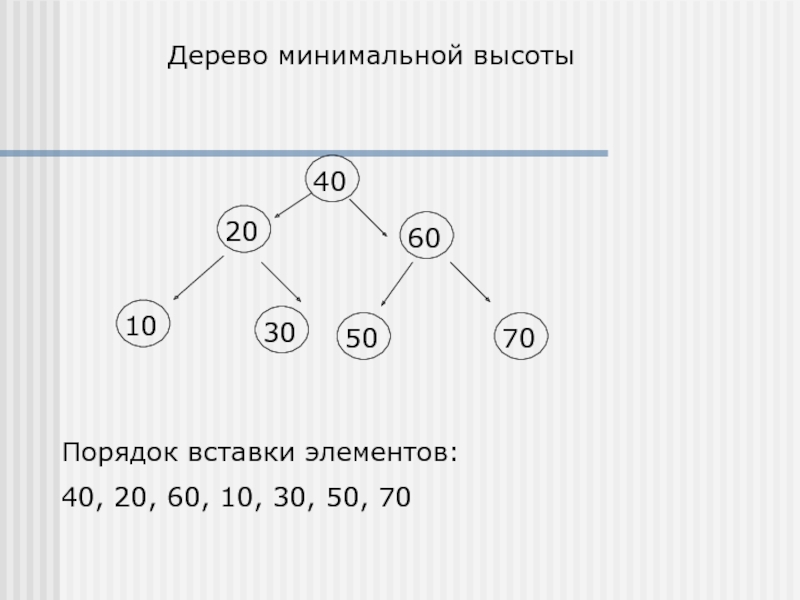
- 9. Дерево минимальной высоты Порядок вставки элементов: 40, 20, 60, 10, 30, 50, 70
- 10. Высота бинарного дерева Высота бинарного дерева
- 11. Цель: Создание деревьев, не теряющих баланса при
- 12. 2-3 дерево Каждый узел 2-3 дерева содержит
- 13. 2-3 дерево Принцип упорядоченности для 2-3 дерева:
- 14. Принцип упорядоченности для 2-3 дерева: Для 3-узла
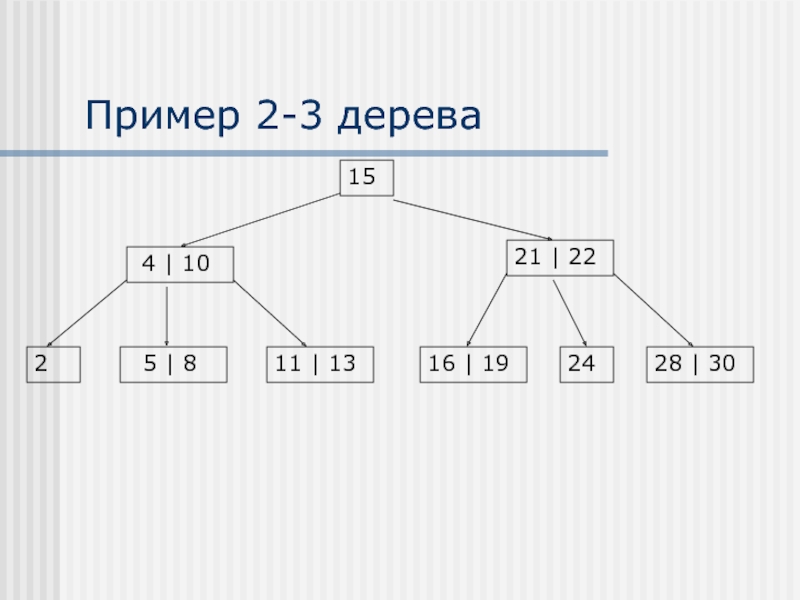
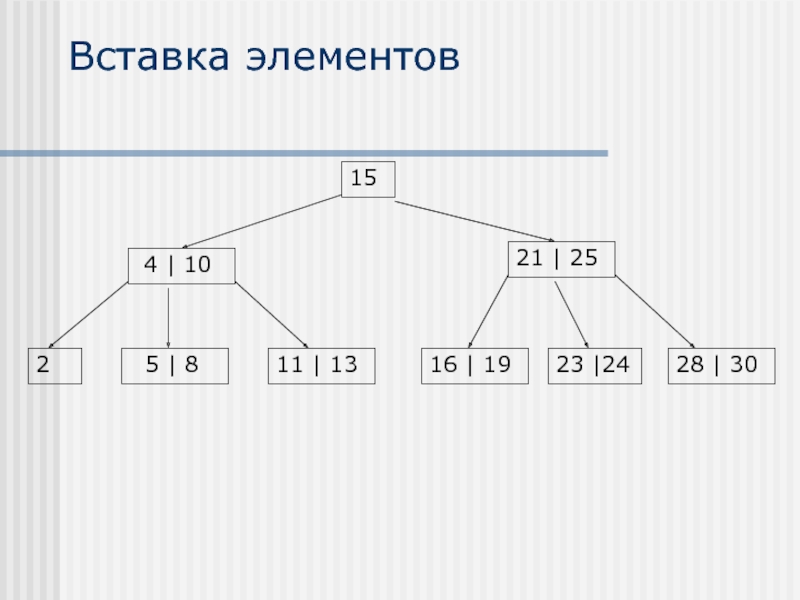
- 15. Пример 2-3 дерева 15 21 |
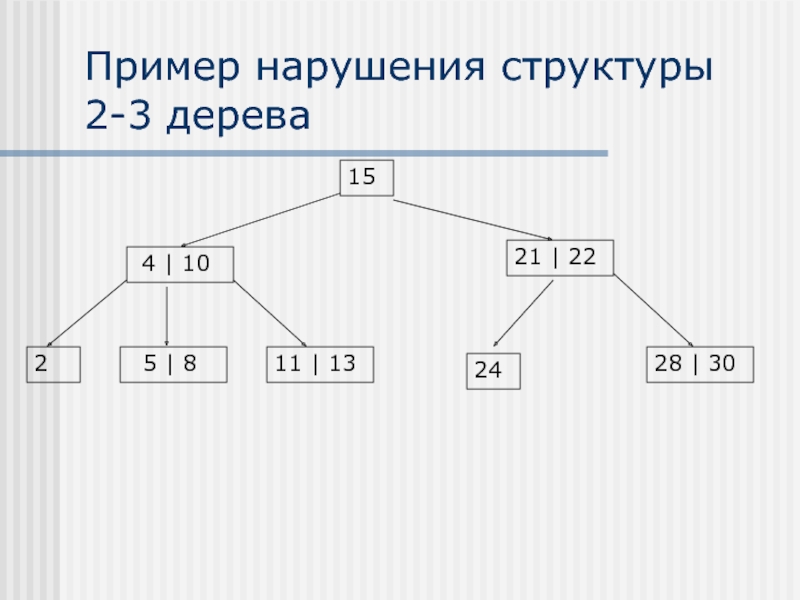
- 16. Пример нарушения структуры 2-3 дерева 15
- 17. 2-3 дерево 2-3 дерево не является бинарным
- 18. Физическое представление 2-3 дерева 15 21
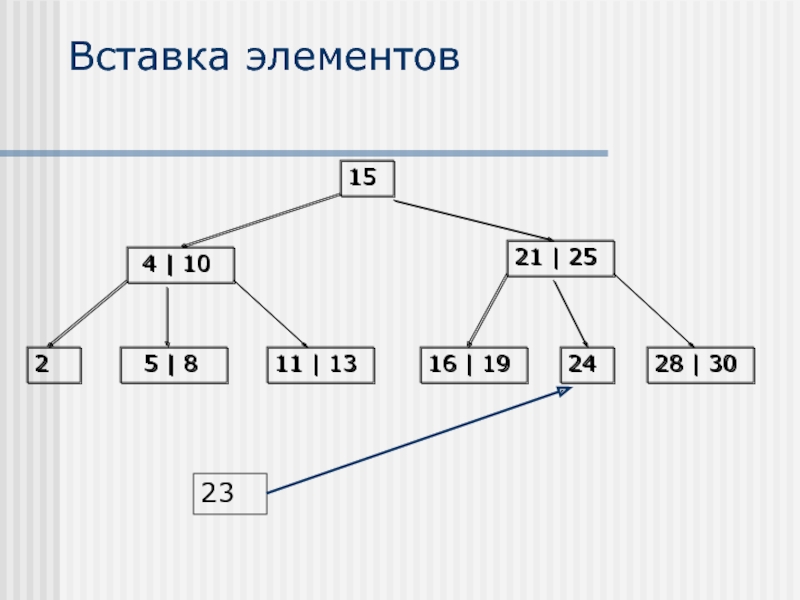
- 19. Вставка элементов Вставка элементов осуществляется только в
- 20. Вставка элементов 23
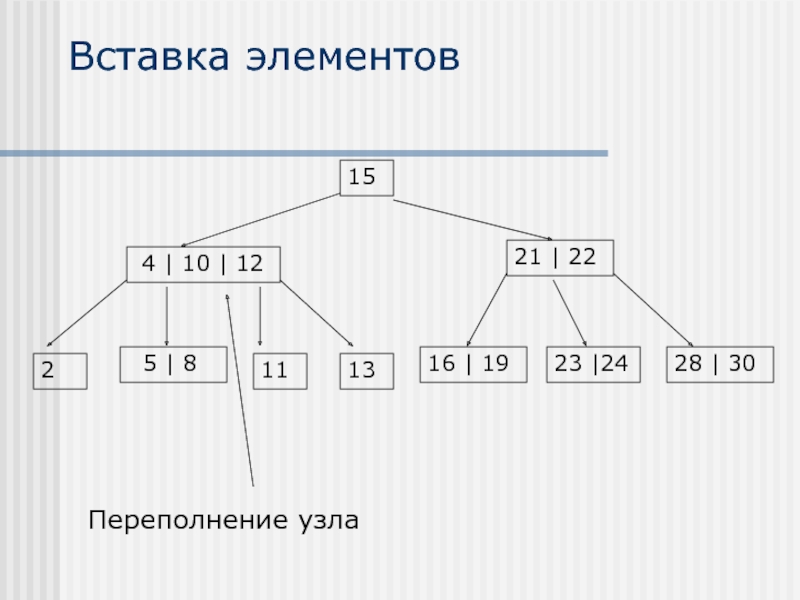
- 21. Вставка элементов
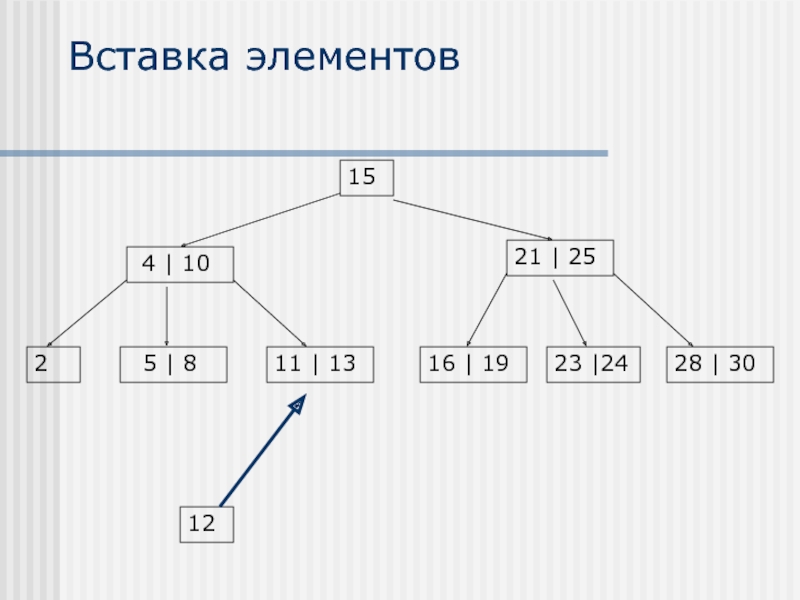
- 22. Вставка элементов 12
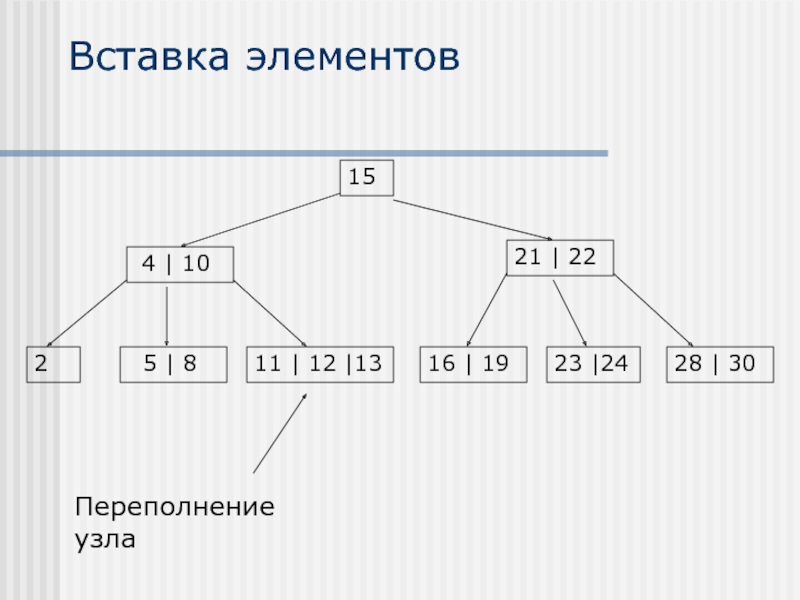
- 23. Вставка элементов 15 21 | 22
- 24. Вставка элементов 15 21 | 22
- 25. Вставка элементов 15 21 | 22
- 26. Вставка элементов 15 21 | 22
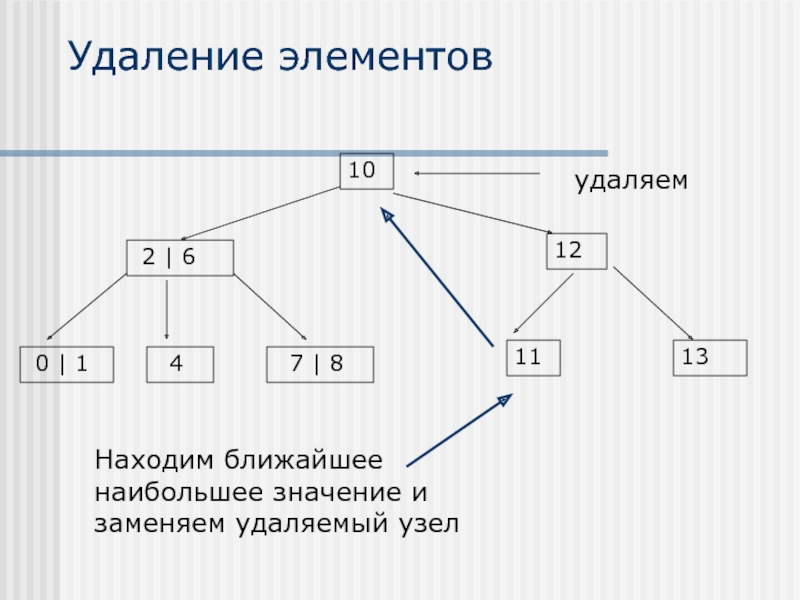
- 27. Удаление элементов Находим ближайшее наибольшее значение и заменяем удаляемый узел
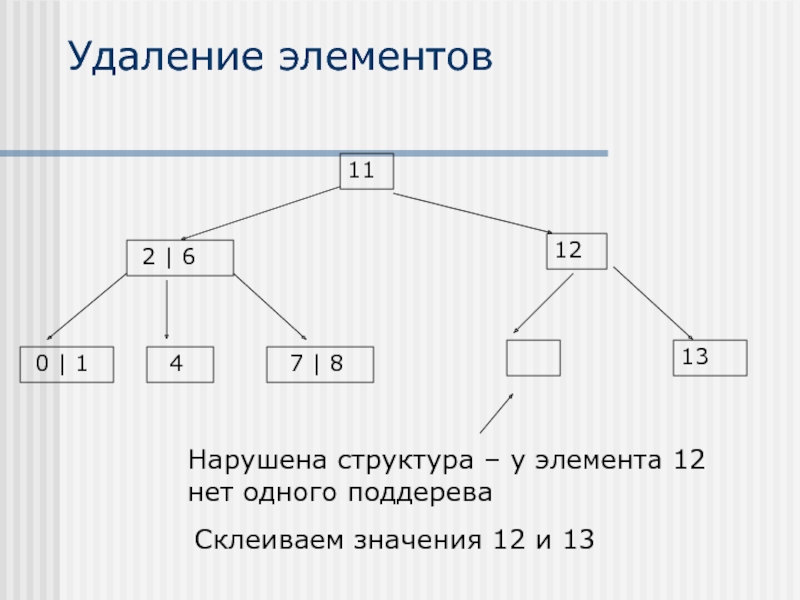
- 28. Удаление элементов Склеиваем значения 12 и 13
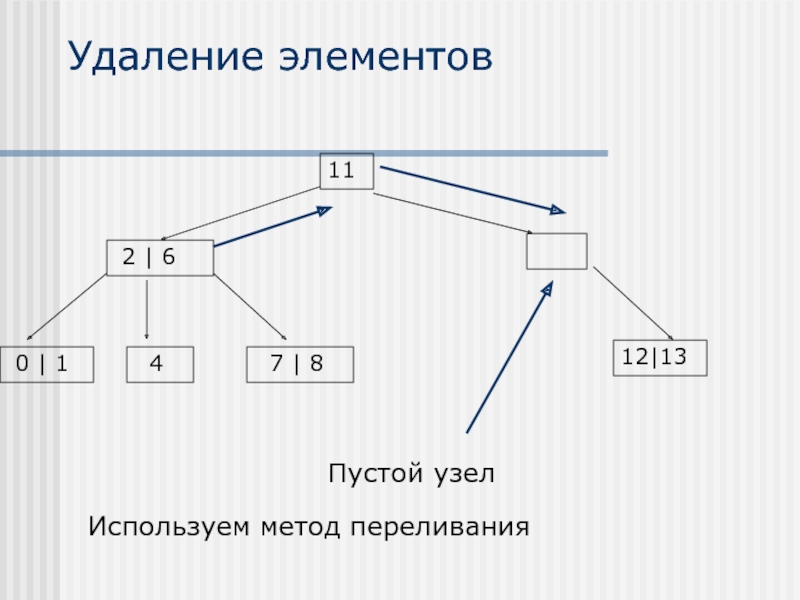
- 29. Удаление элементов Используем метод переливания
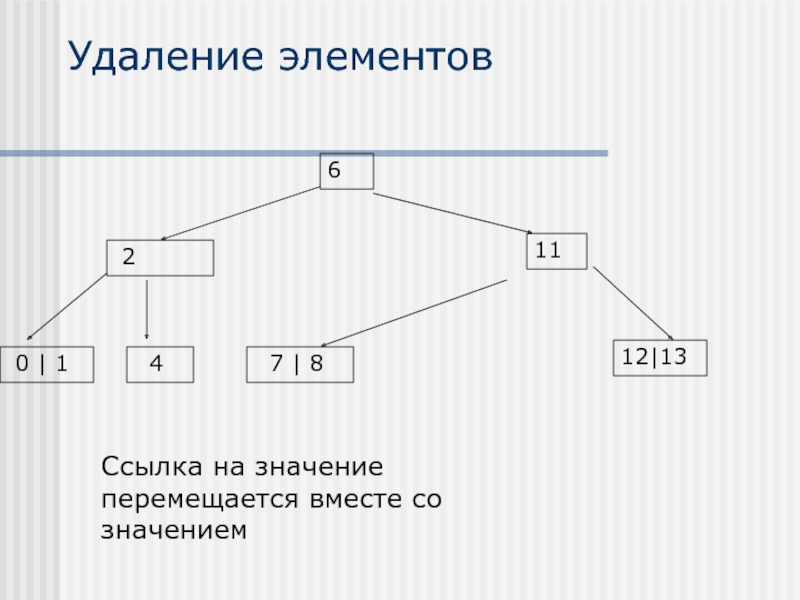
- 30. Удаление элементов 2 6 11
- 31. Преимущества 2-3 дерева 2-3 дерево всегда сбалансировано
- 32. 2-3-4 деревья 2-3-4 дерево может содержать четырехместные
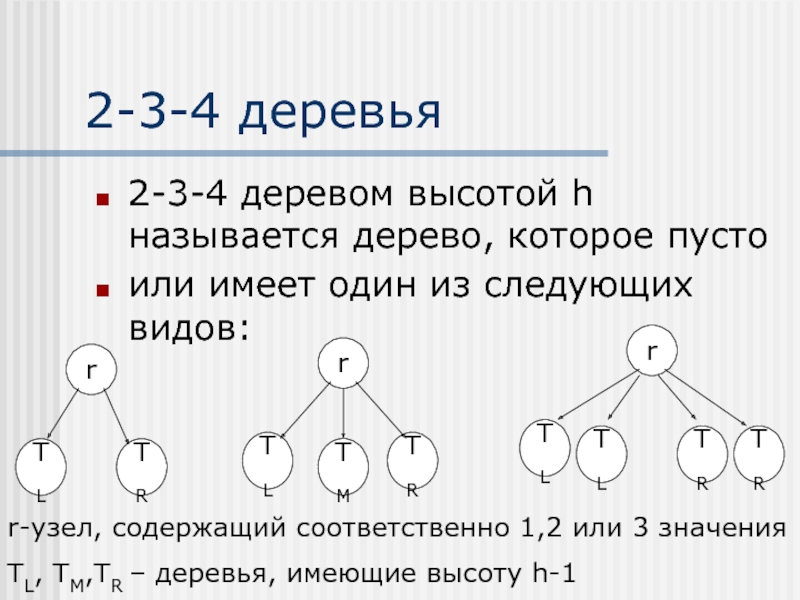
- 33. 2-3-4 деревья 2-3-4 деревом высотой h называется
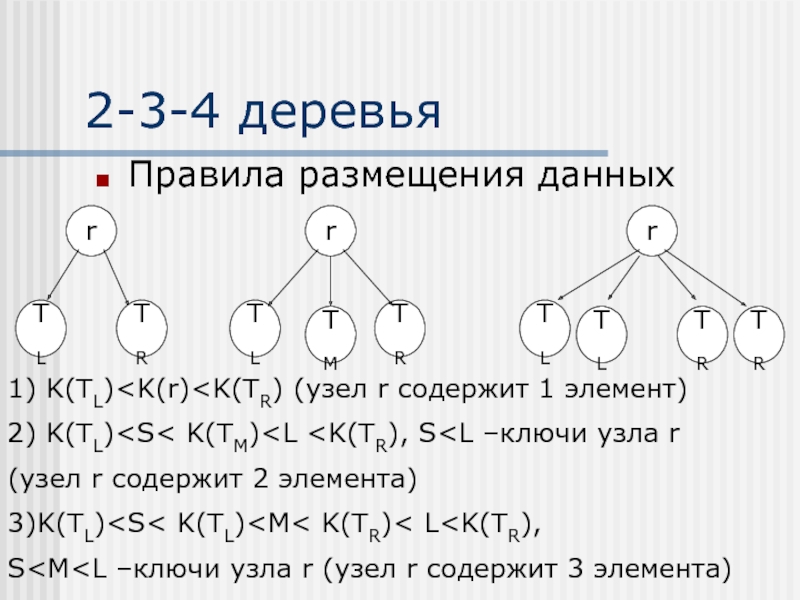
- 34. 2-3-4 деревья Правила размещения данных 1) K(TL)
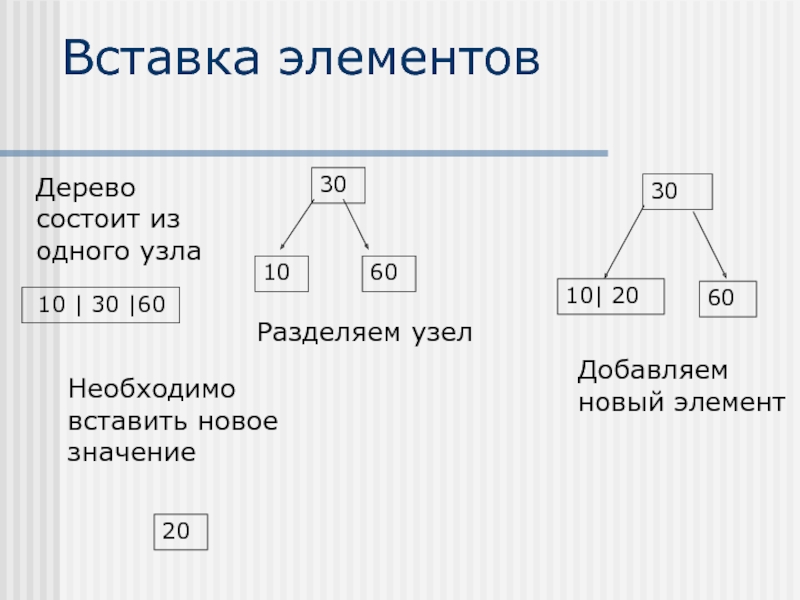
- 35. Вставка элементов Четырехместный узел разделяется сразу после
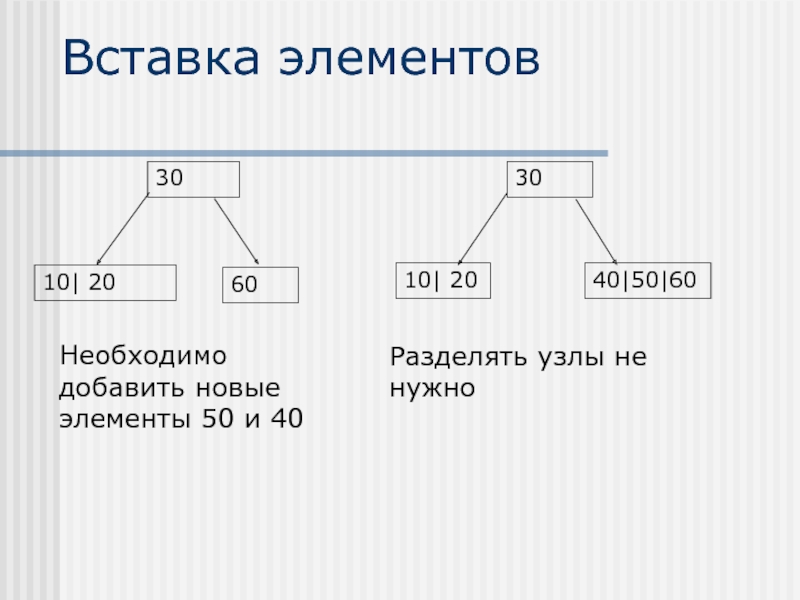
- 36. Вставка элементов
- 37. Вставка элементов
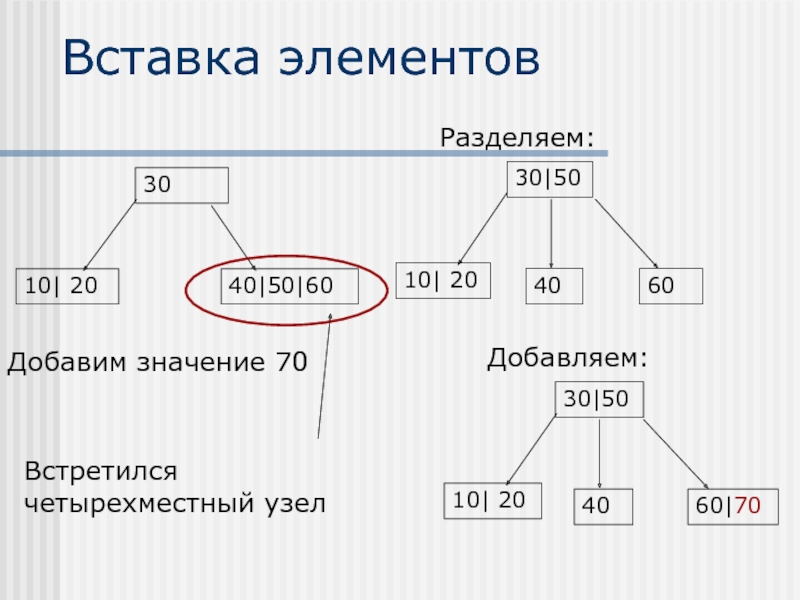
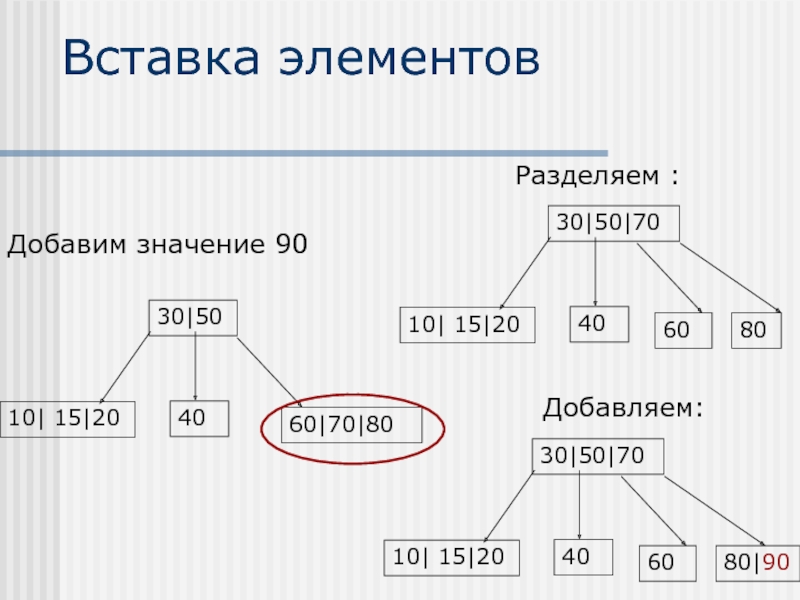
- 38. Вставка элементов Добавим значение 70
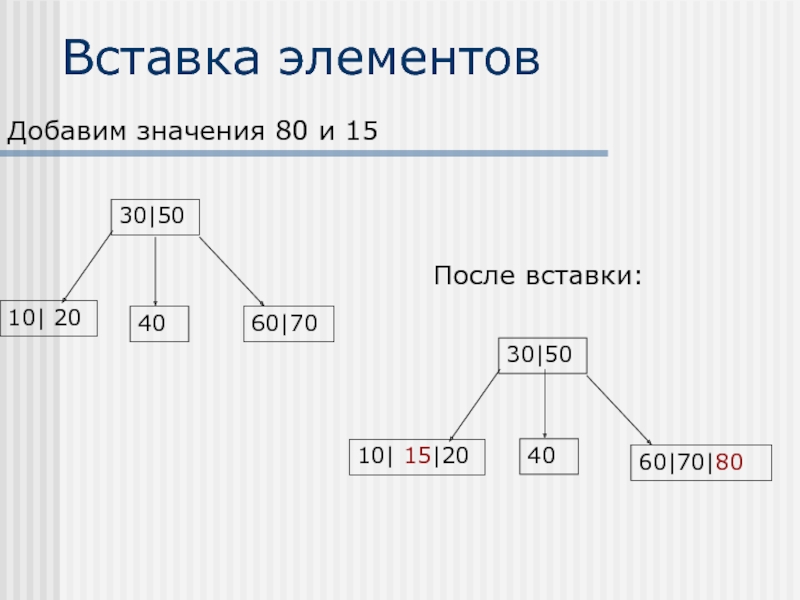
- 39. Вставка элементов Добавим значения 80 и 15
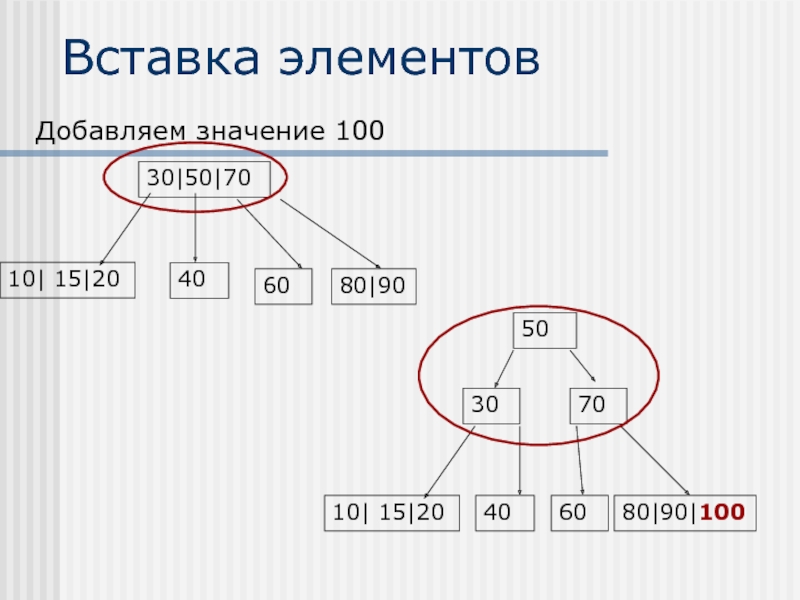
- 40. Вставка элементов
- 41. Вставка элементов
- 42. Разделение четырехместных узлов при вставке Возможны случаи:
- 43. Удаление элементов Находим узел, содержащий данный элемент
- 44. Удаление элементов При проходе дерева во время
- 45. Заключение Достоинства 2-3 и 2-3-4 деревьев заключается
- 46. Заключение Несмотря на то, что высота рассмотренных
Слайд 2Пример:
Необходимо расположить все слова некоторого текста в алфавитном порядке
Для решения данной
Слайд 3Допустим задан текст
«Сэр Исаак Ньютон по секрету признавался друзьям, что он
Слайд 4Текст в алфавитном порядке:
ведет
гравитация
друзьям
знает
Исаак
как
не
но
Ньютон
он
по
почему
признавался себя
секрету
сэр
что
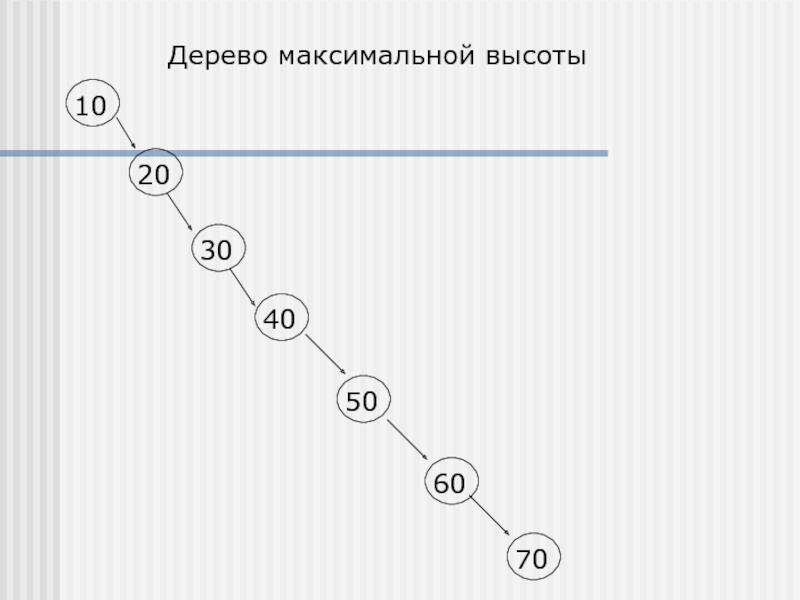
Слайд 7Высота бинарного дерева
Пусть бинарное дерево содержит элементы:10, 20, 30, 40,
Последовательная вставка элементов дает дерево максимальной высоты:
Слайд 10Высота бинарного дерева
Высота бинарного дерева зависит от порядка выполнения операций
Высота бинарного дерева, состоящего из N элементов меняется от log2(N+1) до N
Слайд 11Цель:
Создание деревьев, не теряющих баланса при выполнении операций вставки и удаления
Эффективность
Слайд 122-3 дерево
Каждый узел 2-3 дерева содержит одно или два значения
Узлы дерева
Листья
Промежуточные узлы: Если промежуточный узел содержит одно значение, то он имеет два непустых поддерева (2-узел) Если он содержит два значения, то он имеет три непустых поддерева (3-узел)
Все листья лежат на одном уровне
Слайд 132-3 дерево
Принцип упорядоченности для 2-3 дерева:
Для 2-узла – все значения, лежащие
Слайд 14Принцип упорядоченности для 2-3 дерева:
Для 3-узла – упорядоченность означает следующее:
Пусть А1
K(Т1 )< А1
Слайд 172-3 дерево
2-3 дерево не является бинарным
Все листья 2-3 дерева находятся на
Высота 2-3 дерева никогда не превышает минимальную высоту бинарного дерева, содержащего такое количество элементов
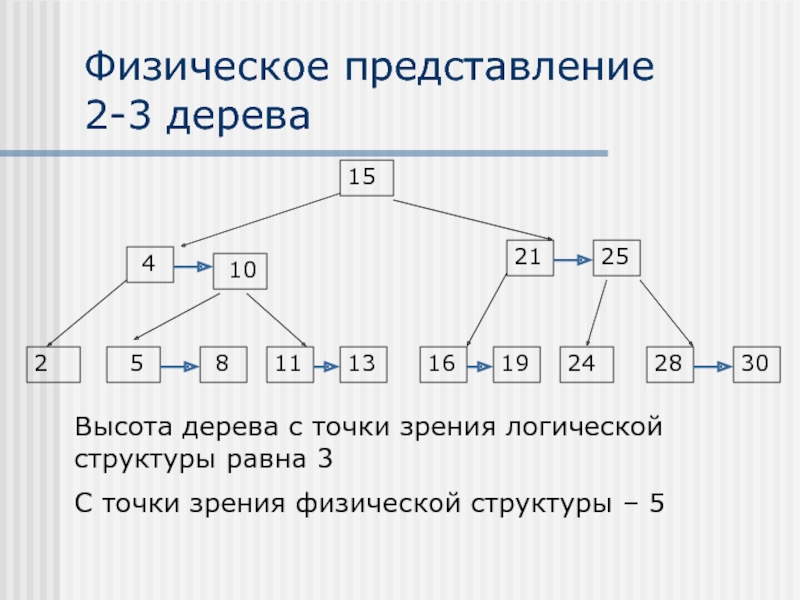
Слайд 18Физическое представление
2-3 дерева
15
21
28
5
4
11
16
2
24
10
8
13
19
30
25
Высота дерева с точки зрения логической структуры равна 3
С точки зрения физической структуры – 5
Слайд 19Вставка элементов
Вставка элементов осуществляется только в листья
В случае, если после вставки
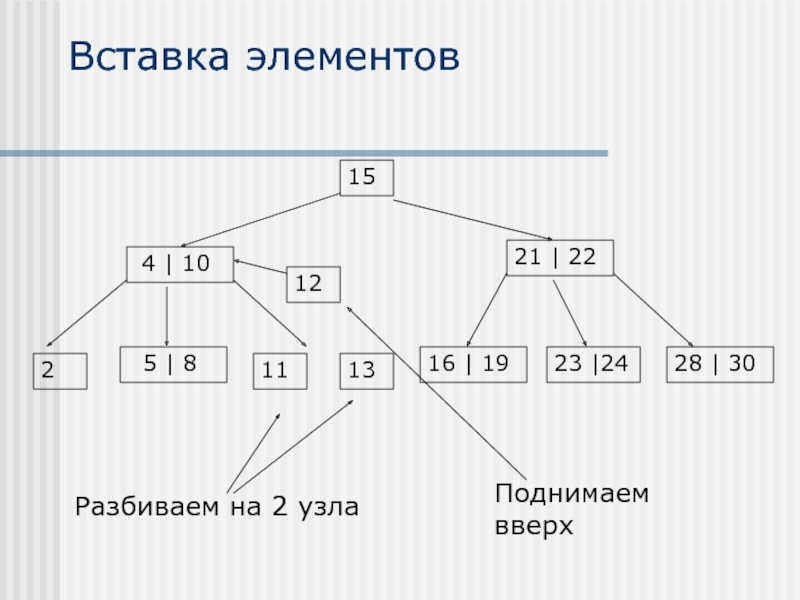
Узел делится на два узла, при этом среднее значение поднимается на уровень выше и присоединяется к узлу на предыдущем уровне
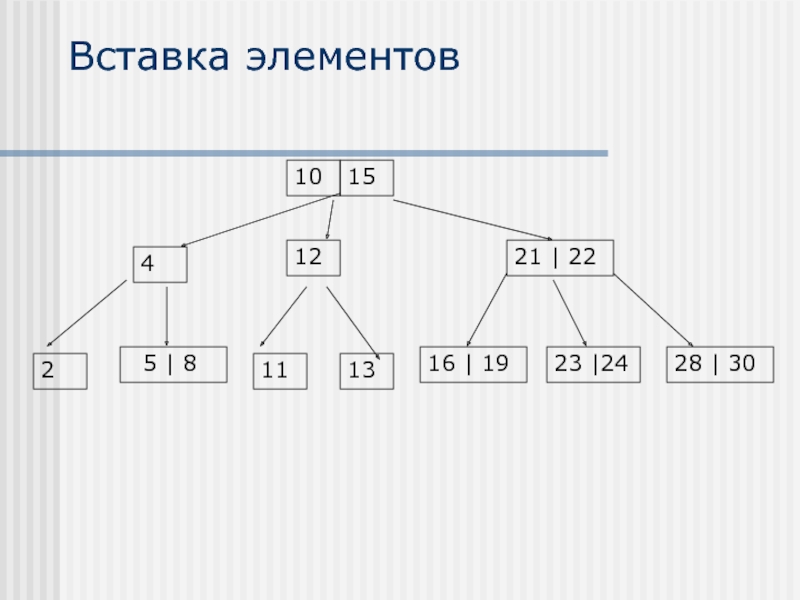
Слайд 24Вставка элементов
15
21 | 22
28 | 30
5 | 8
4 |
16 | 19
12
23 |24
Разбиваем на 2 узла
13
11
2
Поднимаем вверх
Слайд 30Удаление элементов
2
6
11
12|13
4
7 | 8
0 | 1
Ссылка
Слайд 31Преимущества 2-3 дерева
2-3 дерево всегда сбалансировано
Эффективность алгоритма поиска в таком дереве
Слайд 322-3-4 деревья
2-3-4 дерево может содержать четырехместные узлы
По сравнению с 2-3 деревом
Слайд 332-3-4 деревья
2-3-4 деревом высотой h называется дерево, которое пусто
или имеет
r-узел, содержащий соответственно 1,2 или 3 значения
TL, TM,TR – деревья, имеющие высоту h-1
Слайд 35Вставка элементов
Четырехместный узел разделяется сразу после обнаружения, при этом один из
Слайд 42Разделение четырехместных узлов при вставке
Возможны случаи:
Узел является корнем
Узел имеет двухместого родителя
Узел
Слайд 43Удаление элементов
Находим узел, содержащий данный элемент
Заменяем элемент его симметричным преемником (самый
Удаляем элемент из листа
Замечание: в отличие от 2-3 дерева удаление можно осуществить за один проход дерева не перестраивая его
Слайд 44Удаление элементов
При проходе дерева во время поиска элемента, необходимо сразу преобразовать
Замечание: преобразования производятся аналогично процедуре разделения, только в обратном порядке
Слайд 45Заключение
Достоинства 2-3 и 2-3-4 деревьев заключается в том, что они хорошо
Алгоритмы вставки и удаления в 2-3-4 дерево выполняются за меньшее число шагов чем для 2-3 дерева
Слайд 46Заключение
Несмотря на то, что высота рассмотренных деревьев ниже, чем у бинарного
Рассматривать деревья с числом дочерних узлов больше 4-х не имеет смысла, поскольку число сравнений будет очень велико. Их можно применять только если такие деревья реализованы на внешних носителях