преп. каф. ИАНИ, к.т.н.
Исаев С.А.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задачи упаковки кругов с помощью генетических алгоритмов презентация
Содержание
- 1. Решение задачи упаковки кругов с помощью генетических алгоритмов
- 2. Содержательная постановка задачи об упаковке кругов
- 3. Математическая постановка задачи Пусть есть компактная область
- 4. Практическая значимость задачи Укладка объектов цилиндрической формы
- 5. Научная значимость Теорема об упаковке кругов используется теориях конформного отображения и планарных графов.
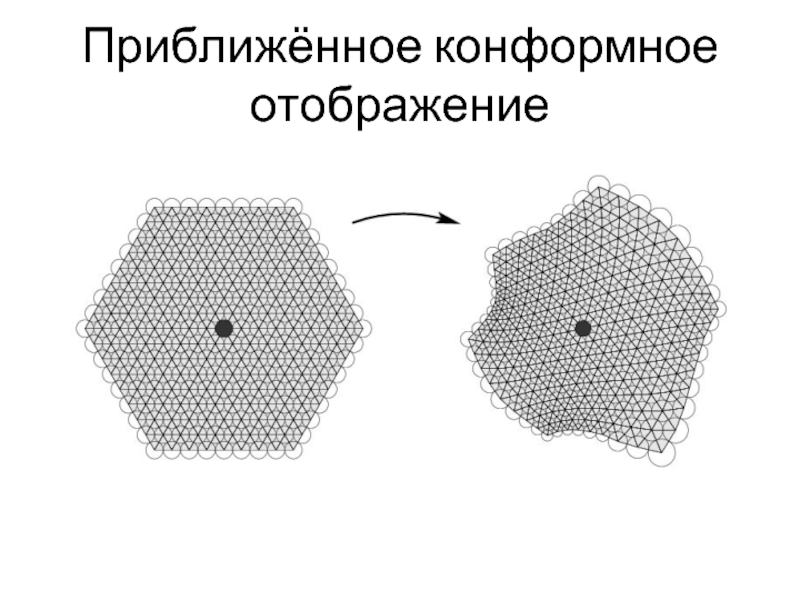
- 6. Приближённое конформное отображение
- 7. Оптимальные упаковки Сейчас известны оптимальные упаковки (с
- 8. Упаковка в единичный квадрат
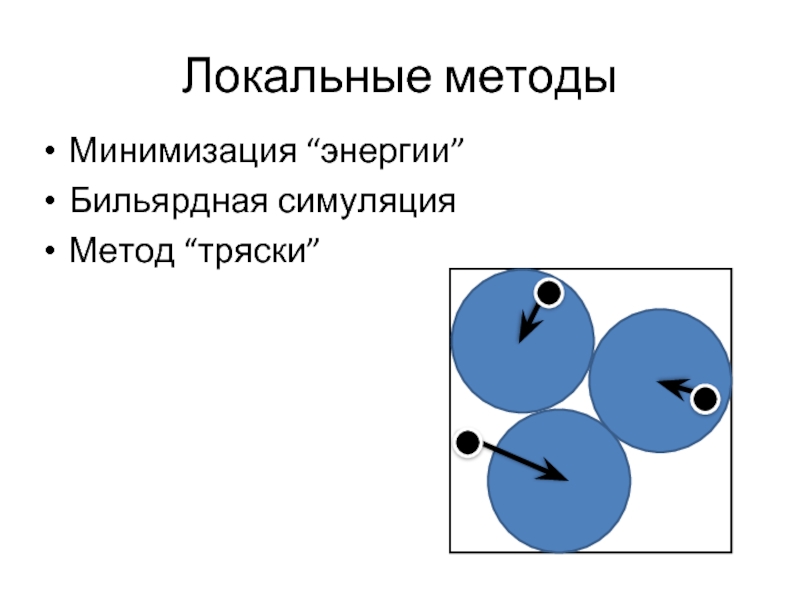
- 9. Локальные методы Минимизация
- 10. Минимизация “энергии” Аналогия с электростатикой; При
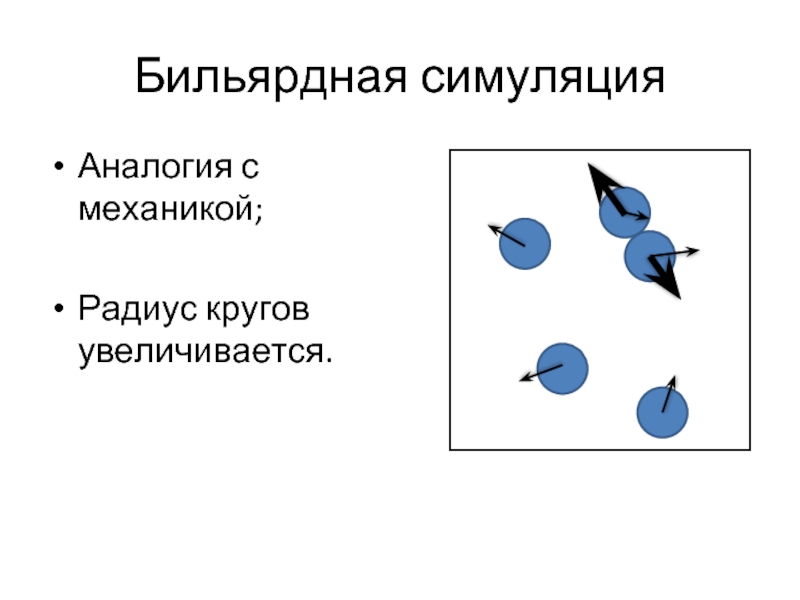
- 11. Бильярдная симуляция Аналогия с механикой; Радиус кругов увеличивается.
- 12. Метод тряски По очереди пытаемся двигать
- 13. Глобальные методы Метод Монте-Карло Дискретизация задачи
- 14. Схема работы ГА Выбираем три случайные особи
- 15. Выбор кодировки Кодировать напрямую: (X1,Y1, … ,
- 16. Прямая кодировка В векторе (X1,Y1, … ,
- 17. Кодировка со сжатием Кодировать в A
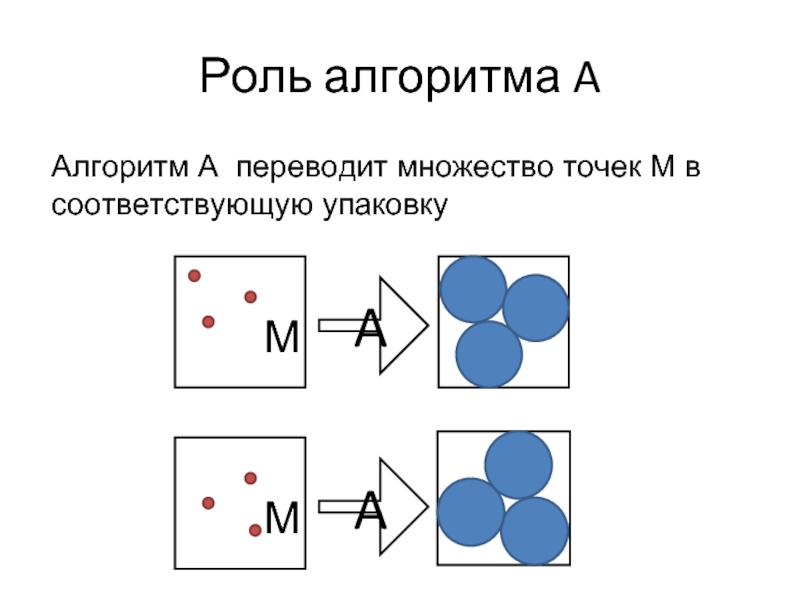
- 18. Кодировка алгоритма Кодировка – пара M
- 19. Роль алгоритма A
- 20. Структура A Идентификатор алгоритма Кол-во итераций
- 21. Пример алгоритма A Каждая точка отталкивается от
- 22. Оператор скрещивания Множество M у потомка определяется
- 23. Наследование алгоритма Потомок наследует алгоритм A у
- 24. Оператор мутации Случайное подмножество M сдвигается на
- 25. Структура оптимальных упаковок начиная с 49 кругов,
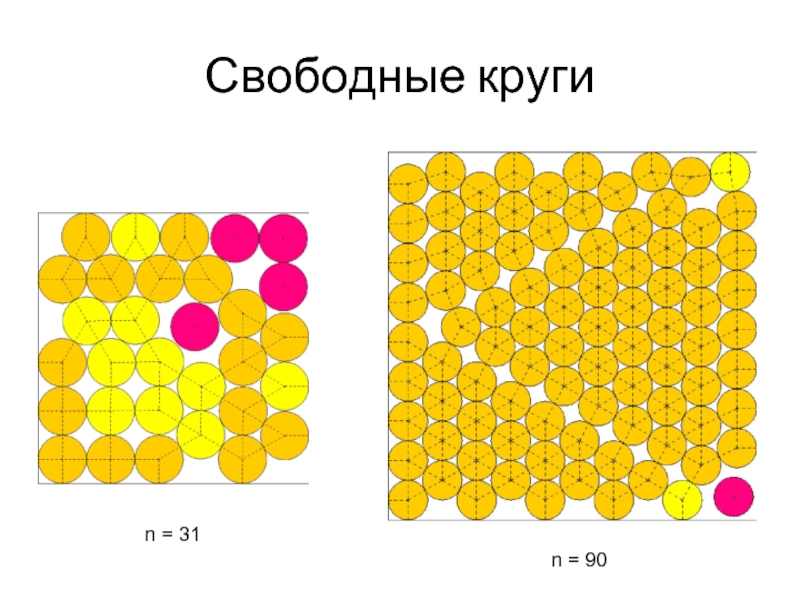
- 26. Свободные круги n = 31 n = 90
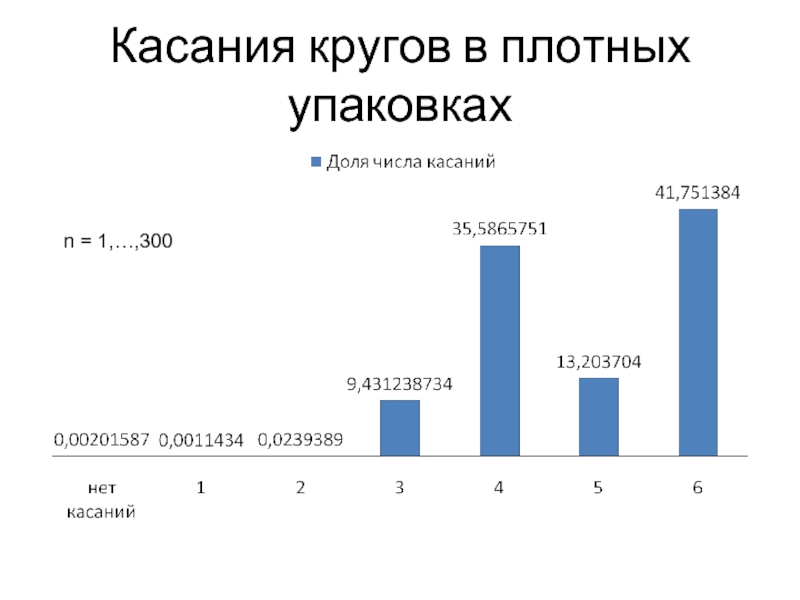
- 27. Касания кругов в плотных упаковках n = 1,…,300
- 28. Использование GPU для вычислений Множество M Конечная
- 29. Упаковка большого числа кругов При увеличении n
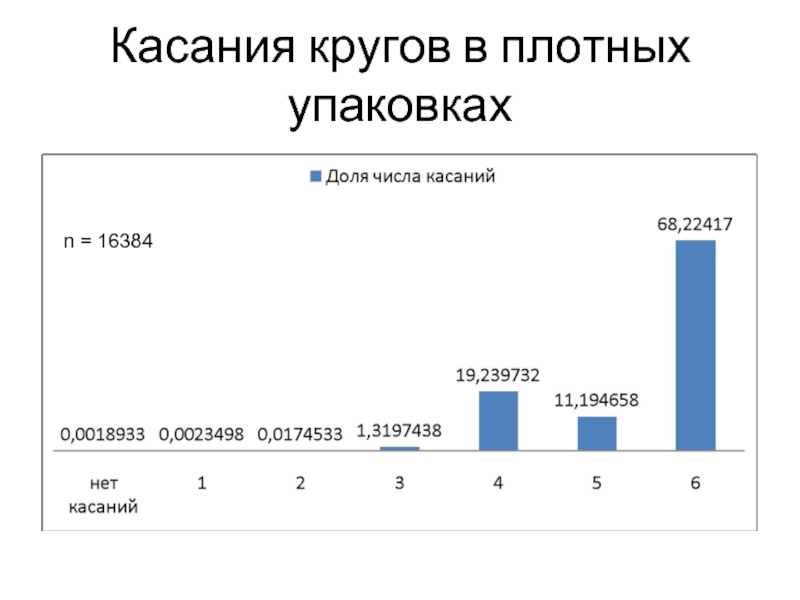
- 30. Касания кругов в плотных упаковках n = 16384
- 31. Выводы Адаптация генетического алгоритма и его гибридизация
- 32. Заключение В ходе выполнения дипломной работы сделано:
Слайд 1Решение задачи упаковки кругов с помощью генетических алгоритмов
Выполнил:
Студент группы 85-05
Гаврилов Н.И.
Руководитель:
ст.
Слайд 2Содержательная постановка задачи об упаковке кругов
Найти максимальный радиус, при
котором N неперекрывающихся кругов могут быть помещены в область упаковки.
Слайд 3Математическая постановка задачи
Пусть есть компактная область D из R².
Найти такие
точки S₁, … ,Sn из D, чтобы максимизировать величину min(R,r),
где
R = min{ |Si – Sj| | i≠j, i,j=1..n}
r = min{ ρ(Si, ∂D) | i=1..n }
ρ(Si, ∂D) – расстояние от точки Si до границы области D
где
R = min{ |Si – Sj| | i≠j, i,j=1..n}
r = min{ ρ(Si, ∂D) | i=1..n }
ρ(Si, ∂D) – расстояние от точки Si до границы области D
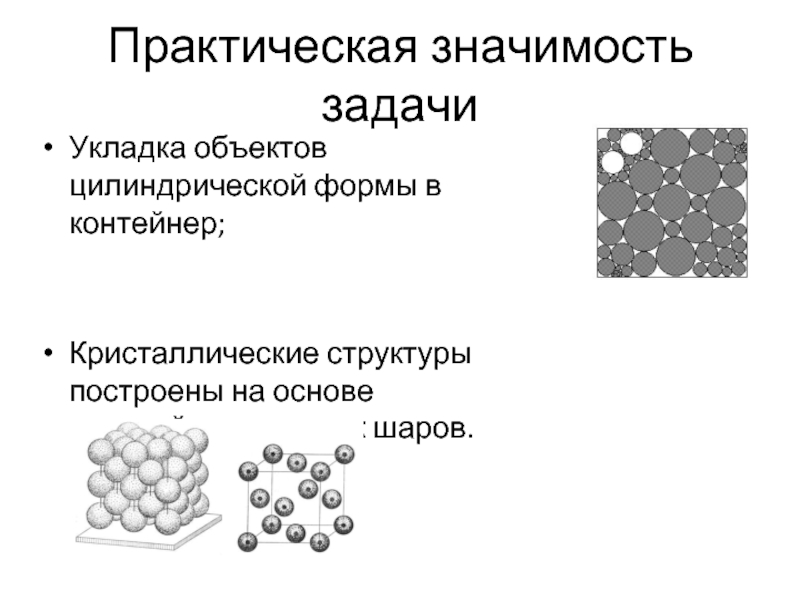
Слайд 4Практическая значимость задачи
Укладка объектов цилиндрической формы в контейнер;
Кристаллические структуры построены на
основе плотнейших укладок шаров.
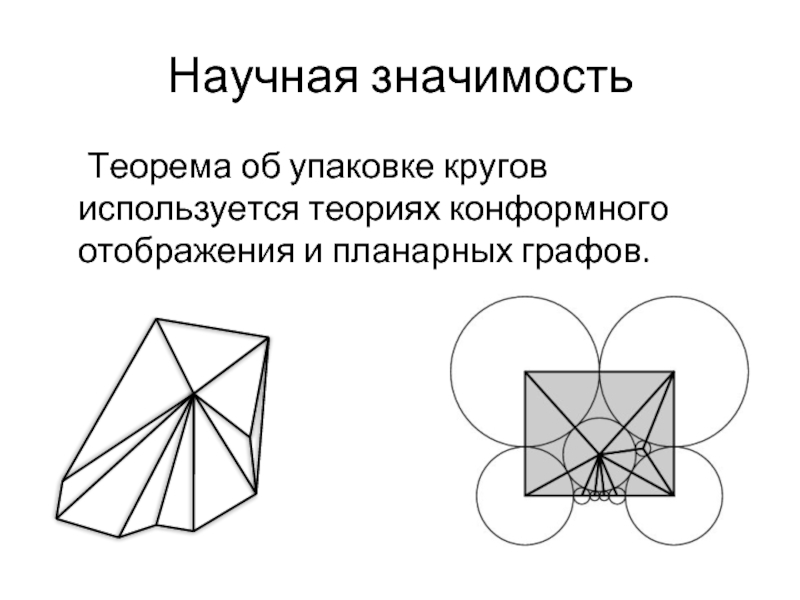
Слайд 5Научная значимость
Теорема об упаковке кругов используется теориях конформного отображения и планарных
графов.
Слайд 7Оптимальные упаковки
Сейчас известны оптимальные упаковки (с доказательством) до n = 36;
Упаковки-кандидаты
– лучшие известные упаковки без доказательства оптимальности (http://www.packomania.com).
Находятся эвристическими методами.
Находятся эвристическими методами.
Слайд 10Минимизация “энергии”
Аналогия с электростатикой;
При замене x’=sin(x),y’=sin(y) получаем задачу без ограничений;
Методом Ньютона
получены упаковки до 50 кругов.
Слайд 12
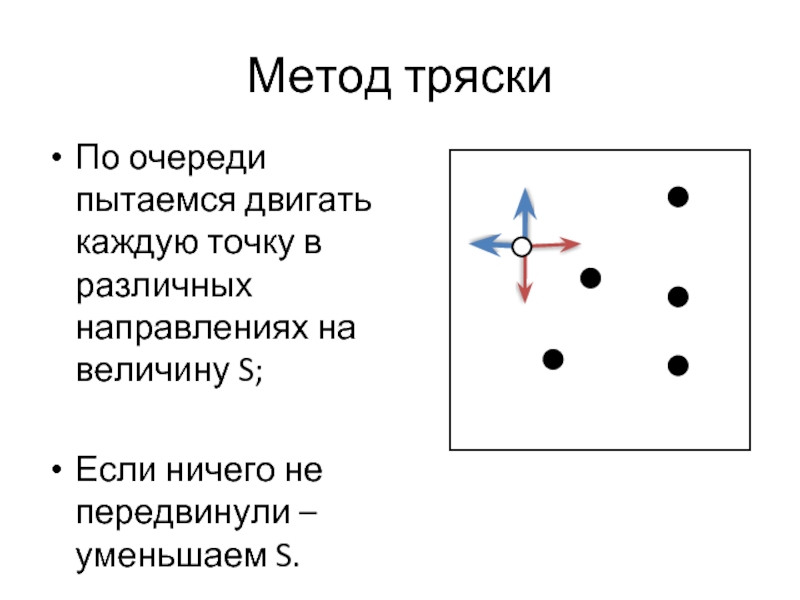
Метод тряски
По очереди пытаемся двигать каждую точку в различных направлениях на
величину S;
Если ничего не передвинули – уменьшаем S.
Если ничего не передвинули – уменьшаем S.
Слайд 13Глобальные методы
Метод Монте-Карло
Дискретизация задачи с последующим перебором.
Эволюционные методы
В качестве приспособленности выступает
радиус кругов, либо размер масштабируемой области упаковки.
Слайд 14Схема работы ГА
Выбираем три случайные особи (A, B и С в
порядке приспособленности)
С вероятностью p особь C замещается потомком от A и B
Иначе особь B замещается потомком от A и C
C вероятностью q потомок мутирует
Если последние K итерации дали улучшения решения, то идём на шаг 2
С вероятностью p особь C замещается потомком от A и B
Иначе особь B замещается потомком от A и C
C вероятностью q потомок мутирует
Если последние K итерации дали улучшения решения, то идём на шаг 2
Слайд 15Выбор кодировки
Кодировать напрямую: (X1,Y1, … , Xn,Yn)
Кодировать со сжатием.
Цель – уменьшить
число неизвестных
Кодировать алгоритм получения плотной упаковки
Кодировать алгоритм получения плотной упаковки
Слайд 16Прямая кодировка
В векторе (X1,Y1, … , Xn,Yn) координаты центров кругов;
Можно кодировать
в (X2,Y2, … , Xn,Yn). Тогда это координаты центров кругов радиуса 1.
Тогда область упаковки масштабируется.
Недостатки:
Много переменных
Сложная область допустимых значений
Много локальных экстремумов
Тогда область упаковки масштабируется.
Недостатки:
Много переменных
Сложная область допустимых значений
Много локальных экстремумов
Слайд 17Кодировка со сжатием
Кодировать в
A = (A[1],…,A[n-1]), B = (B[1],…,B[n-1])
B[i] –
сколько кругов “создаёт” i-ый круг
A[i] – под каким углом “создан” (i+1)-ый круг
A[i] – под каким углом “создан” (i+1)-ый круг
(1,2,1,0,1)
1
2
4
6
5
3
Слайд 18Кодировка алгоритма
Кодировка – пара
M = { Ci | i=1…n,
Ci є D} (область упаковки)
Этими начальными условиями обладают все алгоритмы A;
A – алгоритм упаковки и начальные условия для него;
Этими начальными условиями обладают все алгоритмы A;
A – алгоритм упаковки и начальные условия для него;
Слайд 20Структура A
Идентификатор алгоритма
Кол-во итераций
Вероятности
Параметры, влияющие на скорость сходимости A, и т.д.
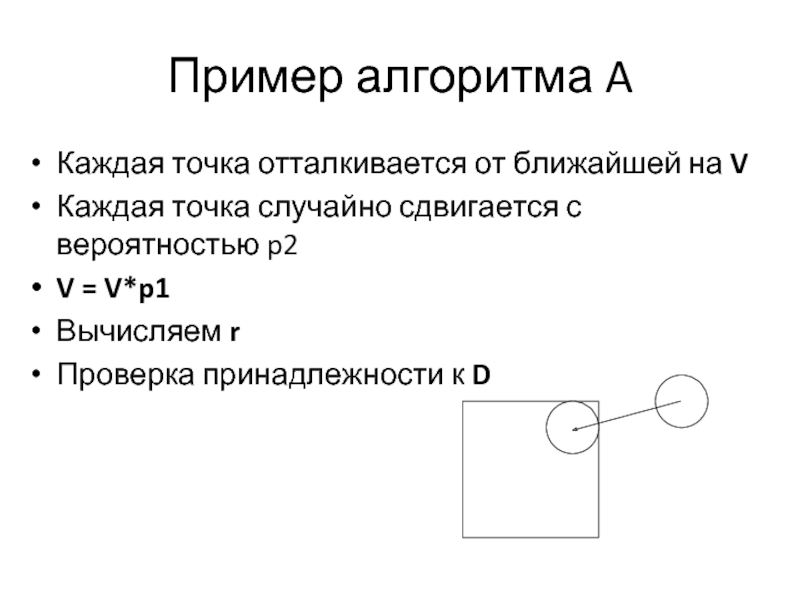
Слайд 21Пример алгоритма A
Каждая точка отталкивается от ближайшей на V
Каждая точка случайно
сдвигается с вероятностью p2
V = V*p1
Вычисляем r
Проверка принадлежности к D
V = V*p1
Вычисляем r
Проверка принадлежности к D
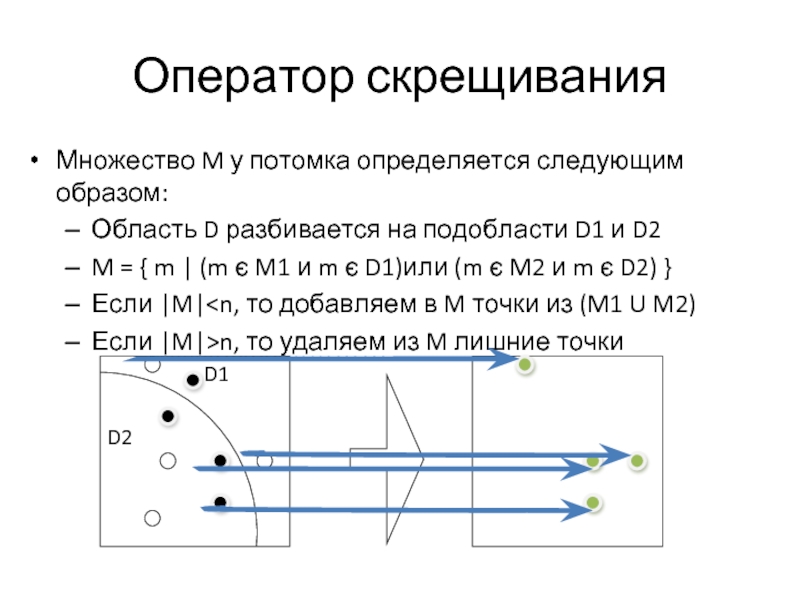
Слайд 22Оператор скрещивания
Множество M у потомка определяется следующим образом:
Область D разбивается на
подобласти D1 и D2
M = { m | (m є M1 и m є D1)или (m є M2 и m є D2) }
Если |M|Если |M|>n, то удаляем из M лишние точки
M = { m | (m є M1 и m є D1)или (m є M2 и m є D2) }
Если |M|
D1
D2
Слайд 23Наследование алгоритма
Потомок наследует алгоритм A у случайного родителя;
Если у родителей одинаковые
схемы алгоритма, то каждый параметр этого алгоритма у потомка также выбирается от случайного родителя.
Слайд 24Оператор мутации
Случайное подмножество M сдвигается на случайные вектора
(dx,dy) =
( a, b)*(n^-½)
a, b – числа из распределения N(0,1)
a, b – числа из распределения N(0,1)
Слайд 25Структура оптимальных упаковок
начиная с 49 кругов, оптимальная упаковка n=k² кругов будет
отлична от регулярной квадратной решётки.
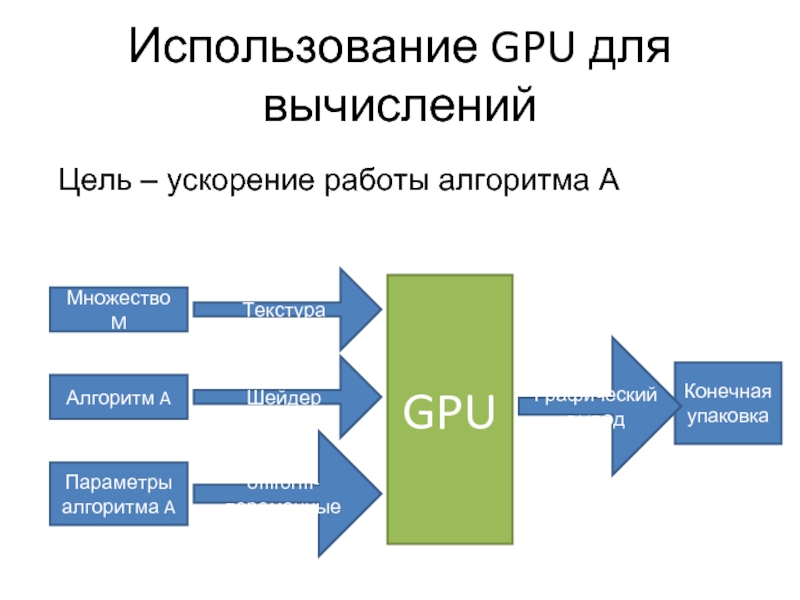
Слайд 28Использование GPU для вычислений
Множество M
Конечная упаковка
Параметры алгоритма A
GPU
Алгоритм A
Текстура
Шейдер
Uniform-переменные
Графический вывод
Цель –
ускорение работы алгоритма A
Слайд 29Упаковка большого числа кругов
При увеличении n появляются большие фрагменты плотнейших кладок
n
= 16384 r = 0.00405794
Слайд 31Выводы
Адаптация генетического алгоритма и его гибридизация с низкоуровневой проблемно-ориентированной эвристикой способна
значительно повысить эффективность применения ГА.
Важным фактором, влияющим на эффективность применения ГА, является выбранный способ кодирования решений.
Важным фактором, влияющим на эффективность применения ГА, является выбранный способ кодирования решений.
Слайд 32Заключение
В ходе выполнения дипломной работы сделано:
Обзор методов решения задачи об упаковке
кругов;
Разработан проблемно-ориентированный генетический подход к решению этой задачи;
Исследованы структуры упаковок, найденных в результате численного эксперимента.
Разработан проблемно-ориентированный генетический подход к решению этой задачи;
Исследованы структуры упаковок, найденных в результате численного эксперимента.










![Кодировка со сжатиемКодировать в A = (A[1],…,A[n-1]), B = (B[1],…,B[n-1])B[i] – сколько кругов “создаёт” i-ый](/img/tmb/2/160188/1caf18020fe389e4864405b6ee93382f-800x.jpg)