- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рекурсивные алгоритмы (C++). Лекция 8 по основам программирования презентация
Содержание
- 1. Рекурсивные алгоритмы (C++). Лекция 8 по основам программирования
- 3. РЕКУРСИВНЫМ называется способ построения объекта, в
- 4. РЕКУРСИЯ Рекурсия – метод определения функции через
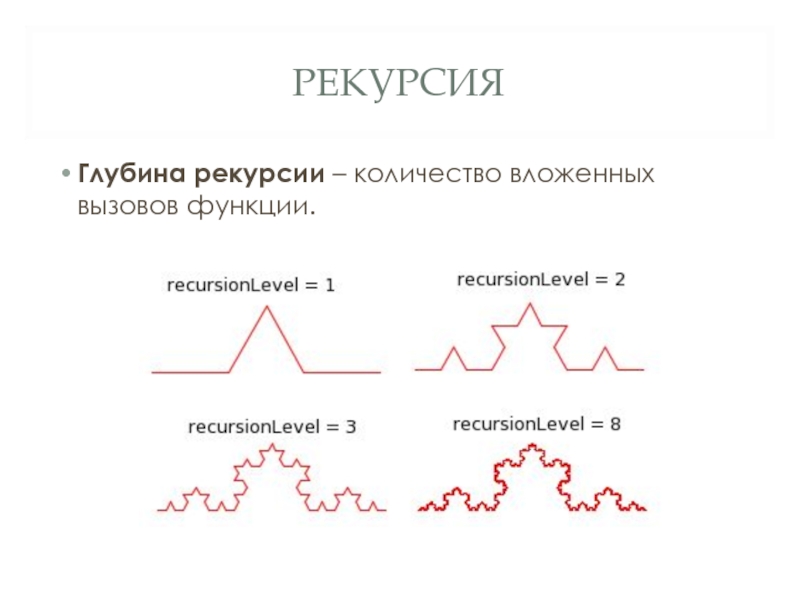
- 5. РЕКУРСИЯ Глубина рекурсии – количество вложенных вызовов функции.
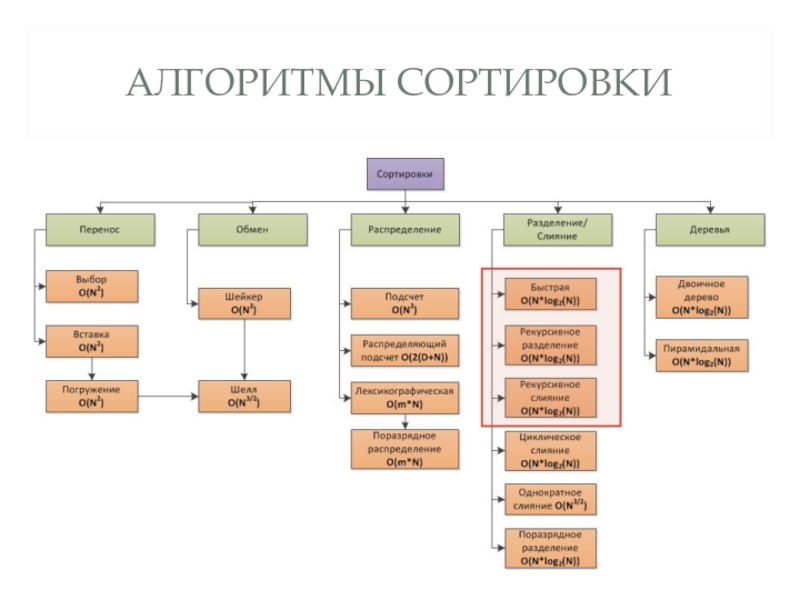
- 6. АЛГОРИТМЫ СОРТИРОВКИ
- 7. АЛГОРИТМЫ СОРТИРОВКИ РЕКУРСИВНЫЕ АЛГОРИТМЫ
- 8. БЫСТРАЯ СОРТИРОВКА Стратегия – «разделяй и властвуй».
- 9. БЫСТРАЯ СОРТИРОВКА
- 10. БЫСТРАЯ СОРТИРОВКА void sort(int in[], int a,
- 11. СОРТИРОВКА СЛИЯНИЕМ Стратегия – «разделяй и властвуй».
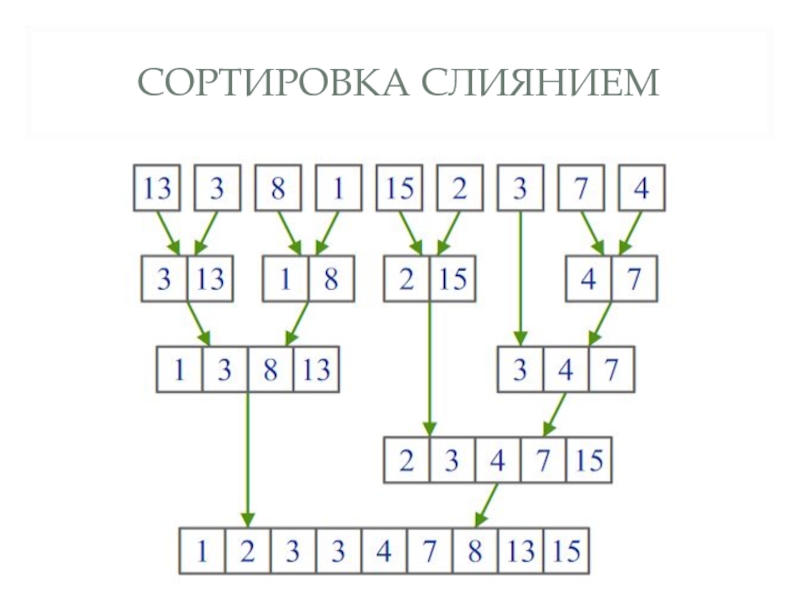
- 12. СОРТИРОВКА СЛИЯНИЕМ
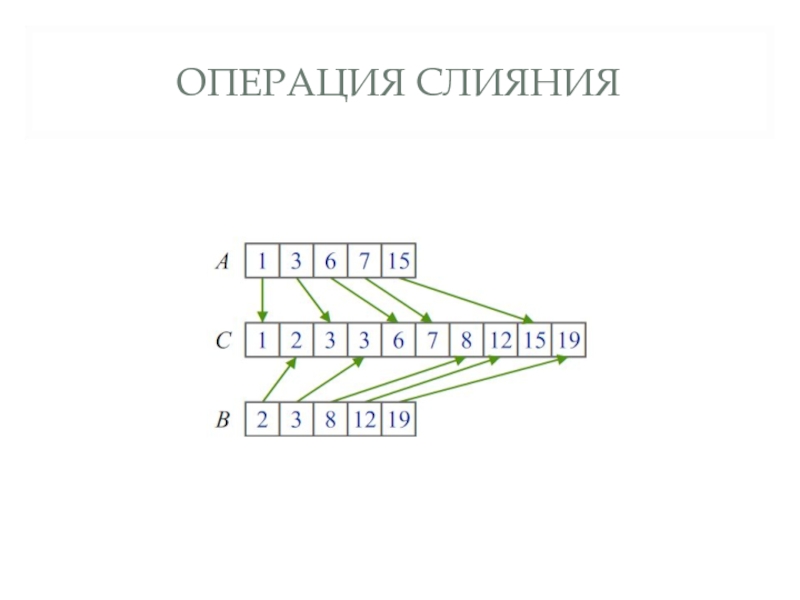
- 13. ОПЕРАЦИЯ СЛИЯНИЯ Отделяем элемент, наименьший из двух
- 14. ОПЕРАЦИЯ СЛИЯНИЯ
- 15. ЗАДАЧИ 1. Реализовать алгоритм сортировки рекурсивным разделением
Слайд 3
РЕКУРСИВНЫМ
называется способ построения объекта, в котором определение объекта включает аналогичные объекты
в виде составных частей.
Слайд 4РЕКУРСИЯ
Рекурсия – метод определения функции через её предыдущие и ранее определенные
значения, а так же способ организации вычислений, при котором функция вызывает сама себя с другим аргументом.
Простая рекурсия – вызов функции из неё же самой непосредственно.
Сложная, или косвенная рекурсия – вызов через другие функции, например, функция а вызывает функцию б, а функция б функцию а.
Простая рекурсия – вызов функции из неё же самой непосредственно.
Сложная, или косвенная рекурсия – вызов через другие функции, например, функция а вызывает функцию б, а функция б функцию а.
Слайд 8БЫСТРАЯ СОРТИРОВКА
Стратегия – «разделяй и властвуй».
Описание алгоритма:
Выбираем в массиве некоторый
элемент, который будем называть опорным элементом.
Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него.
Рекурсивно упорядочиваем подмассивы.
Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него.
Рекурсивно упорядочиваем подмассивы.
Слайд 10БЫСТРАЯ СОРТИРОВКА
void sort(int in[], int a, int b){
int i,j,mode;
if (a>=b) return;
for (i=a, j=b, mode=1; i < j; mode >0 ? j-- : i++)
if (in[i] > in[j]) {
int c = in[i]; in[i] = in[j]; in[j]=c;
mode = -mode;
}
sort(in,a,i-1);
sort(in,i+1,b);
}
Слайд 11СОРТИРОВКА СЛИЯНИЕМ
Стратегия – «разделяй и властвуй».
Описание алгоритма:
Сортируемый массив разбивается на
две части примерно одинакового размера;
Каждая из получившихся частей сортируется отдельно тем же самым алгоритмом;
Два упорядоченных массива половинного размера соединяются в один.
Каждая из получившихся частей сортируется отдельно тем же самым алгоритмом;
Два упорядоченных массива половинного размера соединяются в один.
Слайд 13ОПЕРАЦИЯ СЛИЯНИЯ
Отделяем элемент, наименьший из двух имеющихся в началах исходных массивов, и
присоединяем его к концу результирующего массива.
Элементы переносим до тех пор, пока один из исходных массивов не закончится.
После этого оставшийся «хвост» одного из входных массивов дописывается в конец результирующего массива.
Элементы переносим до тех пор, пока один из исходных массивов не закончится.
После этого оставшийся «хвост» одного из входных массивов дописывается в конец результирующего массива.
Слайд 15ЗАДАЧИ
1. Реализовать алгоритм сортировки рекурсивным разделением списка.
2. Реализовать алгоритм сортировки
рекурсивным слиянием списка.







![БЫСТРАЯ СОРТИРОВКАvoid sort(int in[], int a, int b){int i,j,mode;if (a>=b) return; for (i=a, j=b, mode=1;](/img/tmb/5/474655/61c317004cebdc0bc7ffb6517d81f916-800x.jpg)