- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Работа с файлами (C++). Лекция 6 по основам программирования презентация
Содержание
- 1. Работа с файлами (C++). Лекция 6 по основам программирования
- 2. РАБОТА С ФАЙЛАМИ #include для
- 3. РАБОТА С ФАЙЛАМИ Чтобы привязать тот или
- 4. РАБОТА С ФАЙЛАМИ После открытия файлов и
- 5. РАБОТА С ФАЙЛАМИ Для закрытия ранее открытого
- 6. РАБОТА С ФАЙЛАМИ Также можно использовать в
- 7. ЛИНЕЙНЫЙ ПОИСК Если данные не упорядочены, то
- 8. ДВОИЧНЫЙ (БИНАРНЫЙ) ПОИСК Если данные упорядочены, то
- 9. ДВОИЧНЫЙ (БИНАРНЫЙ) ПОИСК искомый интервал поиска делится
- 10. ПОИСК В НЕУПОРЯДОЧЕННОМ МАССИВЕ Задача: дан одномерный
- 11. БИНАРНЫЙ ПОИСК В УПОРЯДОЧЕННЫХ МАССИВАХ l=0; r=N-1; while (l
- 12. БИНАРНЫЙ ПОИСК ДЛЯ МОНОТОННЫХ ФУНКЦИЙ Задача: для
- 13. БИНАРНЫЙ ПОИСК ПО ОТВЕТУ Пусть у нас
- 14. БИНАРНЫЙ ПОИСК ПО ОТВЕТУ Обычный бинарный поиск
- 15. ЗАДАЧА СОРТИРОВКИ Пусть есть последовательность a0, a1...
- 16. АЛГОРИТМ СОРТИРОВКИ Алгоритм сортировки — это алгоритм
- 17. ОЦЕНКА АЛГОРИТМОВ СОРТИРОВКИ Время сортировки — основной
- 18. ОЦЕНКА АЛГОРИТМОВ СОРТИРОВКИ Память — ряд алгоритмов требует
- 19. ОЦЕНКА АЛГОРИТМОВ СОРТИРОВКИ Устойчивость — устойчивая сортировка
- 20. ОЦЕНКА АЛГОРИТМОВ СОРТИРОВКИ Использование операции сравнения. Алгоритмы,
- 21. КЛАССИФИКАЦИЯ АЛГОРИТМОВ СОРТИРОВКИ Признаками классификации могут быть:
- 22. КЛАССИФИКАЦИЯ АЛГОРИТМОВ СОРТИРОВКИ
- 23. КВАДРАТИЧНЫЕ И СУБКВАДРАТИЧНЫЕ АЛГОРИТМЫ СОРТИРОВКИ НЕ ИСПОЛЬЗУЮЩИЕ ДОПОЛНИТЕЛЬНУЮ ПАМЯТЬ
- 24. СОРТИРОВКА ПУЗЫРЬКОМ При проходе снизу вверх по
- 25. СОРТИРОВКА ПУЗЫРЬКОМ Производился ли на i-проходе обмен?
- 26. СРАВНИТЕЛЬНЫЙ АНАЛИЗ Среднее количество сравнений, хоть и
- 27. СОРТИРОВКА ВЫБОРОМ Идея метода состоит в том,
- 28. СОРТИРОВКА ВЫБОРОМ На i-м шаге выбираем min(a[i]
- 29. СОРТИРОВКА ВЫБОРОМ n + (n-1) + (n-2)
- 30. СОРТИРОВКА ВСТАВКАМИ В сортировке пузырьком на i-м
- 31. СОРТИРОВКА ВСТАВКАМИ На следующем, (i+1)-м каждом шаге
- 32. СОРТИРОВКА ВСТАВКАМИ Таким образом, в процессе вставки
- 33. СОРТИРОВКА ВСТАВКАМИ Аналогично сортировке выбором, среднее, а
- 34. СОРТИРОВКА ВСТАВКАМИ Заметим, что на каждом шаге
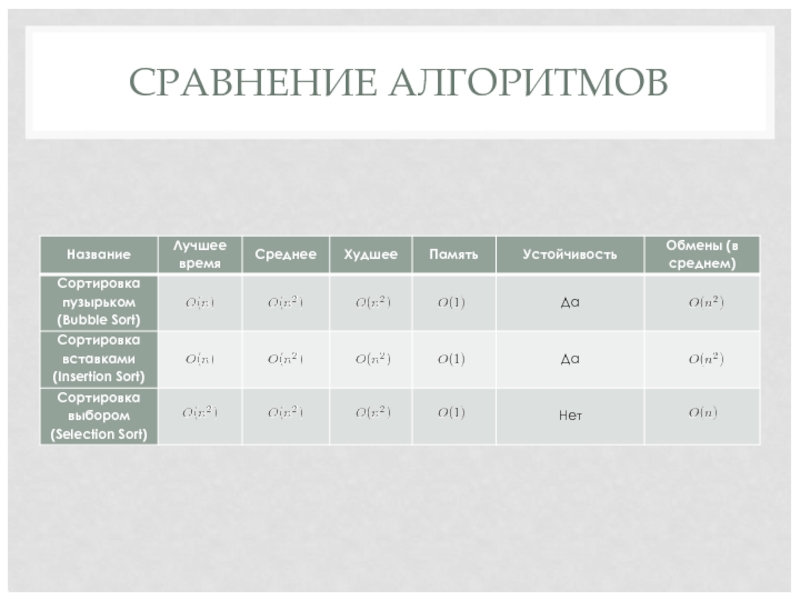
- 35. СРАВНЕНИЕ АЛГОРИТМОВ
- 36. СОРТИРОВКА ШЕЛЛА Алгоритм сортировки массива a[0].. a[15].
- 37. СОРТИРОВКА ШЕЛЛА
- 38. СОРТИРОВКА ШЕЛЛА Приращение - расстояние между сортируемыми
- 39. СРАВНЕНИЕ АЛГОРИТМОВ коричневая: пузырьком; синяя: шейкерная;
- 40. КОНТРОЛЬНАЯ РАБОТА N2 Алгоритмы сортировки реализовать в
РАБОТА С ФАЙЛАМИ #include для чтения данных из файла используются объекты типа ifstream (input file stream) для записи данных в файл используются объекты типа ofstream (output file stream).
Слайд 2РАБОТА С ФАЙЛАМИ
#include
для чтения данных из файла используются объекты типа
ifstream (input file stream)
для записи данных в файл используются объекты типа ofstream (output file stream).
ifstream in; // Поток in для чтения
ofstream out; // Поток out для записи
для записи данных в файл используются объекты типа ofstream (output file stream).
ifstream in; // Поток in для чтения
ofstream out; // Поток out для записи
Слайд 3РАБОТА С ФАЙЛАМИ
Чтобы привязать тот или иной поток к файлу (открыть
файл для чтения или для записи) используется метод open, которому необходимо передать параметр – текстовую строку, содержащую имя открываемого файла.
in.open("input.txt");
out.open("output.txt");
in.open("input.txt");
out.open("output.txt");
Слайд 4РАБОТА С ФАЙЛАМИ
После открытия файлов и привязки их к файловым потокам,
работать с файлами можно так же, как со стандартными потоками ввода-вывода cin и cout.
out<
in>>x;
out<
in>>x;
Слайд 5РАБОТА С ФАЙЛАМИ
Для закрытия ранее открытого файла используется метод close() без
аргументов:
in.close();
out.close();
Закрытый файловый поток можно переоткрыть заново при помощи метода open, привязав его к тому же или другому файлу.
in.close();
out.close();
Закрытый файловый поток можно переоткрыть заново при помощи метода open, привязав его к тому же или другому файлу.
Слайд 6РАБОТА С ФАЙЛАМИ
Также можно использовать в качестве условия результат, возвращаемой операцией
считывания. Если считывание было удачным, то результат считается истиной, а если неудачным – ложью.
Считывание последовательности целых чисел:
int d; while(in>>d) { }
Считывание последовательности целых чисел:
int d; while(in>>d) { }
Слайд 7ЛИНЕЙНЫЙ ПОИСК
Если данные не упорядочены, то найти искомый элемент можно только
путем последовательного перебора всех элементов.
for (i=0; i if (A[i]==B) break;
if (i != n) ...найден...
Поиск значения путем последовательного перебора всех элементов называется линейным поиском.
Сложность алгоритма - O(N).
for (i=0; i
if (i != n) ...найден...
Поиск значения путем последовательного перебора всех элементов называется линейным поиском.
Сложность алгоритма - O(N).
Слайд 8ДВОИЧНЫЙ (БИНАРНЫЙ) ПОИСК
Если данные упорядочены, то найти искомый элемент можно значительно
быстрее.
Алгоритм двоичного или бинарного поиска основан на делении пополам текущего интервала поиска. В основе его лежит тот факт, что при однократном сравнении искомого элемента и некоторого элемента массива мы можем определить, справа или слева от текущего следует искать.
Алгоритм двоичного или бинарного поиска основан на делении пополам текущего интервала поиска. В основе его лежит тот факт, что при однократном сравнении искомого элемента и некоторого элемента массива мы можем определить, справа или слева от текущего следует искать.
Слайд 9ДВОИЧНЫЙ (БИНАРНЫЙ) ПОИСК
искомый интервал поиска делится пополам и по значению элемента
массива в точке деления определяется, в какой части следует искать значение на следующем шаге цикла;
для выбранного интервала поиск повторяется;
при «сжатии» интервала в 0 поиск прекращается;
в качестве начального интервала выбирается весь массив.
Сложность алгоритма - O(log(N)).
для выбранного интервала поиск повторяется;
при «сжатии» интервала в 0 поиск прекращается;
в качестве начального интервала выбирается весь массив.
Сложность алгоритма - O(log(N)).
Слайд 10ПОИСК В НЕУПОРЯДОЧЕННОМ МАССИВЕ
Задача: дан одномерный неупорядоченный массив, состоящий из целых
чисел. Проверить, содержится ли данное число в этом массиве.
Простой метод (последнее вхождение):
int j = -1;
for (i=0; i < n; i++)
if (a[i] == k) j = i;
«Барьерный» метод (первое вхождение):
a[n+1] = k;
for (i=0; a[i] != k; i++);
Простой метод (последнее вхождение):
int j = -1;
for (i=0; i < n; i++)
if (a[i] == k) j = i;
«Барьерный» метод (первое вхождение):
a[n+1] = k;
for (i=0; a[i] != k; i++);
Слайд 12БИНАРНЫЙ ПОИСК ДЛЯ МОНОТОННЫХ ФУНКЦИЙ
Задача: для данного вещественного числа x (x≥1)
найти кубический корень с заданной точностью.
r = x;
l = 1;
while (fabs(l-r)>eps) {
m=(l+r)/2;
if (m*m*melse r=m;
}
r = x;
l = 1;
while (fabs(l-r)>eps) {
m=(l+r)/2;
if (m*m*m
}
Слайд 13БИНАРНЫЙ ПОИСК ПО ОТВЕТУ
Пусть у нас есть функция f, которая принимает
значения "истина" (1) или "ложь" (0), заданная на множестве [0..maxval].
При этом она обладает тем свойством, что сначала все значения истинны, а потом все ложны. [1, 1, ... , 1, 0, 0, ... , 0] - значения функции.
Иначе говоря, это означает, что
(f(x) и y <= x) => f(y).
Искомый элемент - самая правая единица в массиве (к отсортированному массиву применяется обычный бинарный поиск).
При этом она обладает тем свойством, что сначала все значения истинны, а потом все ложны. [1, 1, ... , 1, 0, 0, ... , 0] - значения функции.
Иначе говоря, это означает, что
(f(x) и y <= x) => f(y).
Искомый элемент - самая правая единица в массиве (к отсортированному массиву применяется обычный бинарный поиск).
Слайд 14БИНАРНЫЙ ПОИСК ПО ОТВЕТУ
Обычный бинарный поиск - частный случай бинарного поиска
по ответу.
Пусть нам дан массив, отсортированный по возрастанию. Требуется найти самое правое вхождение элемента key в массив.
Тогда положим f(x) = (x <= key).
Задача сведена к бинарному поиску по ответу.
Пусть нам дан массив, отсортированный по возрастанию. Требуется найти самое правое вхождение элемента key в массив.
Тогда положим f(x) = (x <= key).
Задача сведена к бинарному поиску по ответу.
Слайд 15ЗАДАЧА СОРТИРОВКИ
Пусть есть последовательность a0, a1... an и функция сравнения, которая на
любых двух элементах последовательности принимает одно из трех значений: меньше, больше или равно.
Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие: ai <= ai+1, для всех i от 0 до n.
Задача сортировки состоит в перестановке членов последовательности таким образом, чтобы выполнялось условие: ai <= ai+1, для всех i от 0 до n.
Слайд 16АЛГОРИТМ СОРТИРОВКИ
Алгоритм сортировки — это алгоритм для упорядочения элементов в последовательности.
Та
часть элемента данных, которая идентифицирует его и используется для поиска, называется ключом.
Остальная часть несет в себе содержательную информацию, которая извлекается и используется из найденного элемента данных.
Остальная часть несет в себе содержательную информацию, которая извлекается и используется из найденного элемента данных.
Слайд 17ОЦЕНКА АЛГОРИТМОВ СОРТИРОВКИ
Время сортировки — основной параметр, характеризующий быстродействие алгоритма. Называется
также вычислительной сложностью. Для сортировки важны худшее, среднее и лучшее поведения алгоритма в терминах размера последовательности n.
Для типичного алгоритма хорошее поведение — это O(n log n) и плохое поведение — это O(n2).
Идеальное поведение для сортировки — O(n).
Для типичного алгоритма хорошее поведение — это O(n log n) и плохое поведение — это O(n2).
Идеальное поведение для сортировки — O(n).
Слайд 18ОЦЕНКА АЛГОРИТМОВ СОРТИРОВКИ
Память — ряд алгоритмов требует выделения дополнительной памяти под временное
хранение данных. Как правило, эти алгоритмы требуют O(log n) памяти. При оценке не учитывается место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы (так как всё это потребляет O(1)). Алгоритмы сортировки, не потребляющие дополнительной памяти, относят к сортировкам на месте.
Слайд 19ОЦЕНКА АЛГОРИТМОВ СОРТИРОВКИ
Устойчивость — устойчивая сортировка не меняет взаимного расположения элементов
с одинаковыми ключами.
Естественность поведения — эффективность метода при обработке уже упорядоченных или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.
Естественность поведения — эффективность метода при обработке уже упорядоченных или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.
Слайд 20ОЦЕНКА АЛГОРИТМОВ СОРТИРОВКИ
Использование операции сравнения. Алгоритмы, использующие для сортировки сравнение элементов
между собой, называются основанными на сравнениях.
Минимальная трудоемкость худшего случая для этих алгоритмов составляет O(n log n), но они отличаются гибкостью применения.
Для специальных случаев (типов данных) существуют более эффективные алгоритмы.
Минимальная трудоемкость худшего случая для этих алгоритмов составляет O(n log n), но они отличаются гибкостью применения.
Для специальных случаев (типов данных) существуют более эффективные алгоритмы.
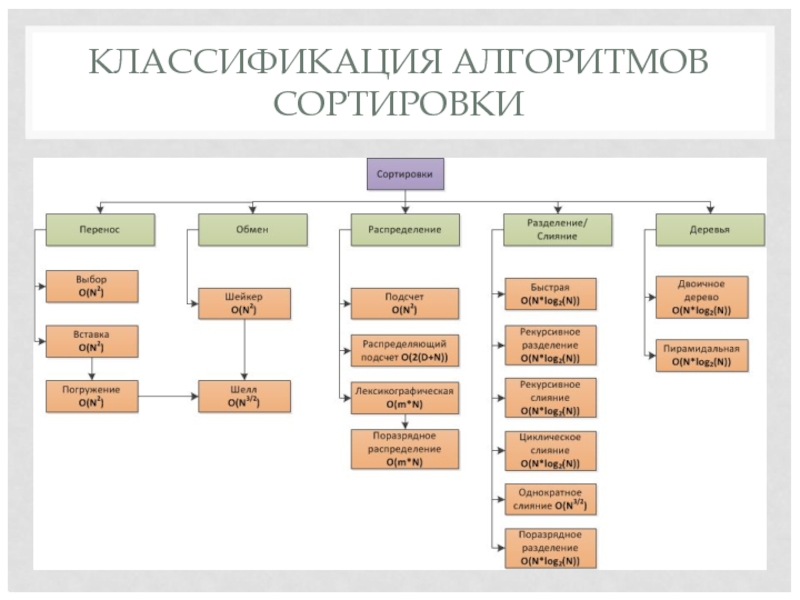
Слайд 21КЛАССИФИКАЦИЯ АЛГОРИТМОВ СОРТИРОВКИ
Признаками классификации могут быть:
структуры данных, используемые при сортировке (массивы,
списки, деревья),
местонахождение данных – в памяти (внутренняя) и в файлах (внешняя).
эффективность (трудоемкость) алгоритмов.
местонахождение данных – в памяти (внутренняя) и в файлах (внешняя).
эффективность (трудоемкость) алгоритмов.
Слайд 24СОРТИРОВКА ПУЗЫРЬКОМ
При проходе снизу вверх по массиву сравниваются пары соседних элементов.
Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами.
Слайд 25СОРТИРОВКА ПУЗЫРЬКОМ
Производился ли на i-проходе обмен? Если нет - алгоритм заканчивает
работу.
Шейкер-сортировка: направление следующих один за другим проходов меняется.
Шейкер-сортировка: направление следующих один за другим проходов меняется.
Слайд 26СРАВНИТЕЛЬНЫЙ АНАЛИЗ
Среднее количество сравнений, хоть и уменьшилось, но остается O(n2), в
то время как число обменов не изменилось. Среднее(оно же худшее) количество операций остается квадратичным.
Дополнительная память не требуется.
Поведение усовершенствованного (но не начального) метода довольно естественное, почти отсортированный массив будет отсортирован намного быстрее случайного.
Сортировка пузырьком устойчива, однако шейкер-сортировка утрачивает это качество.
Дополнительная память не требуется.
Поведение усовершенствованного (но не начального) метода довольно естественное, почти отсортированный массив будет отсортирован намного быстрее случайного.
Сортировка пузырьком устойчива, однако шейкер-сортировка утрачивает это качество.
Слайд 27СОРТИРОВКА ВЫБОРОМ
Идея метода состоит в том, чтобы создавать отсортированную последовательность путем
присоединения к ней одного элемента за другим в правильном порядке.
Будем строить готовую последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)-м.
Будем строить готовую последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)-м.
Слайд 28СОРТИРОВКА ВЫБОРОМ
На i-м шаге выбираем min(a[i] ... a[n]) и меняем его
местами с a[i].
Вне зависимости от номера текущего шага i, последовательность a[0]...a[i] является упорядоченной.
Вне зависимости от номера текущего шага i, последовательность a[0]...a[i] является упорядоченной.
Слайд 29СОРТИРОВКА ВЫБОРОМ
n + (n-1) + (n-2) + (n-3) + ... +
1 = 1/2 * ( n2+n ) = T (n2)
Результат ее сортировки можно увидеть уже после шага 0, так как больше обменов не будет. Порядок ключей 2a, 2b был изменен на 2b, 2a, так что метод неустойчив.
Если входная последовательность почти упорядочена, то сравнений будет столько же, значит алгоритм ведет себя неестественно.
Результат ее сортировки можно увидеть уже после шага 0, так как больше обменов не будет. Порядок ключей 2a, 2b был изменен на 2b, 2a, так что метод неустойчив.
Если входная последовательность почти упорядочена, то сравнений будет столько же, значит алгоритм ведет себя неестественно.
Слайд 30СОРТИРОВКА ВСТАВКАМИ
В сортировке пузырьком на i-м шаге элементы a[0]...a[i] стоят на
правильных местах и никуда более не переместятся.
При сортировке вставками последовательность a[0]...a[i] упорядочена. (более слабое утверждение)
При этом по ходу алгоритма в нее будут вставляться все новые элементы.
При сортировке вставками последовательность a[0]...a[i] упорядочена. (более слабое утверждение)
При этом по ходу алгоритма в нее будут вставляться все новые элементы.
Слайд 31СОРТИРОВКА ВСТАВКАМИ
На следующем, (i+1)-м каждом шаге алгоритма берем a[i+1] и вставляем
на нужное место в готовую часть массива.
Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним.
В зависимости от результата сравнения элемент либо остается на текущем месте(вставка завершена), либо они меняются местами и процесс повторяется.
Поиск подходящего места для очередного элемента входной последовательности осуществляется путем последовательных сравнений с элементом, стоящим перед ним.
В зависимости от результата сравнения элемент либо остается на текущем месте(вставка завершена), либо они меняются местами и процесс повторяется.
Слайд 32СОРТИРОВКА ВСТАВКАМИ
Таким образом, в процессе вставки мы "просеиваем" элемент x к
началу массива, останавливаясь в случае, когда:
1. Найден элемент, меньший x или
2. Достигнуто начало последовательности.
1. Найден элемент, меньший x или
2. Достигнуто начало последовательности.
Слайд 33СОРТИРОВКА ВСТАВКАМИ
Аналогично сортировке выбором, среднее, а также худшее число сравнений и
пересылок оцениваются как T(n2).
Дополнительная память не используется.
Хорошим показателем сортировки является весьма естественное поведение: почти отсортированный массив будет досортирован очень быстро.
Алгоритм устойчив.
Дополнительная память не используется.
Хорошим показателем сортировки является весьма естественное поведение: почти отсортированный массив будет досортирован очень быстро.
Алгоритм устойчив.
Слайд 34СОРТИРОВКА ВСТАВКАМИ
Заметим, что на каждом шаге внутреннего цикла проверяются 2 условия.
Можно объединить из в одно, поставив в начало массива специальный сторожевой элемент. Он должен быть заведомо меньше всех остальных элементов массива.
Тогда при j=0 будет заведомо верно a[0] <= x. Цикл остановится на нулевом элементе, что и было целью условия j>=0.
Для окончания сортировки возвращаем элемент.
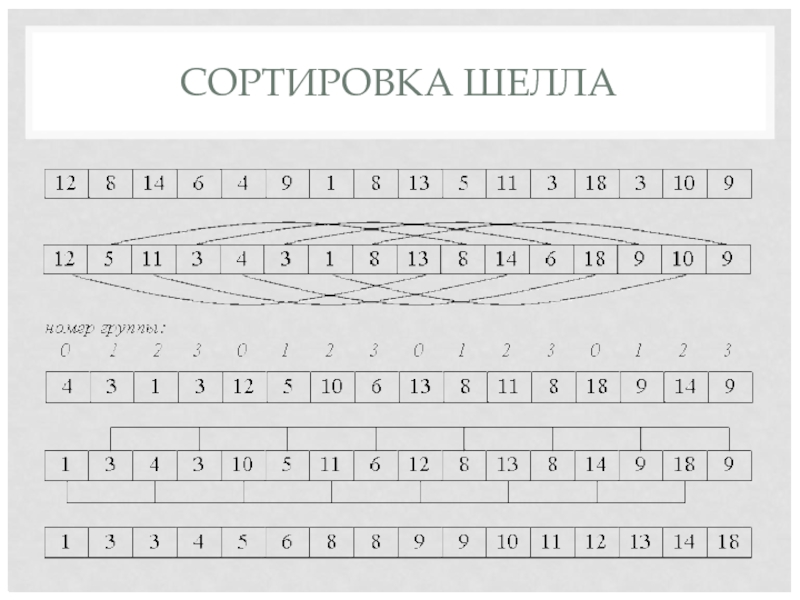
Слайд 36СОРТИРОВКА ШЕЛЛА
Алгоритм сортировки массива a[0].. a[15].
Вначале сортируем простыми вставками каждые 8
групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).
Далее сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).
Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).
В конце сортируем вставками все 16 элементов.
Далее сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).
Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).
В конце сортируем вставками все 16 элементов.
Слайд 38СОРТИРОВКА ШЕЛЛА
Приращение - расстояние между сортируемыми элементами, в зависимости от прохода.
Формула
Седжвика:
последовательность вычисляется в порядке, противоположном используемому.
начальное приращение выбирается по правилу: начинаем с inc[s-1], если 3*inc[s] > size.
среднее количество операций: O(n7/6), в худшем случае - порядка O(n4/3).
последовательность вычисляется в порядке, противоположном используемому.
начальное приращение выбирается по правилу: начинаем с inc[s-1], если 3*inc[s] > size.
среднее количество операций: O(n7/6), в худшем случае - порядка O(n4/3).
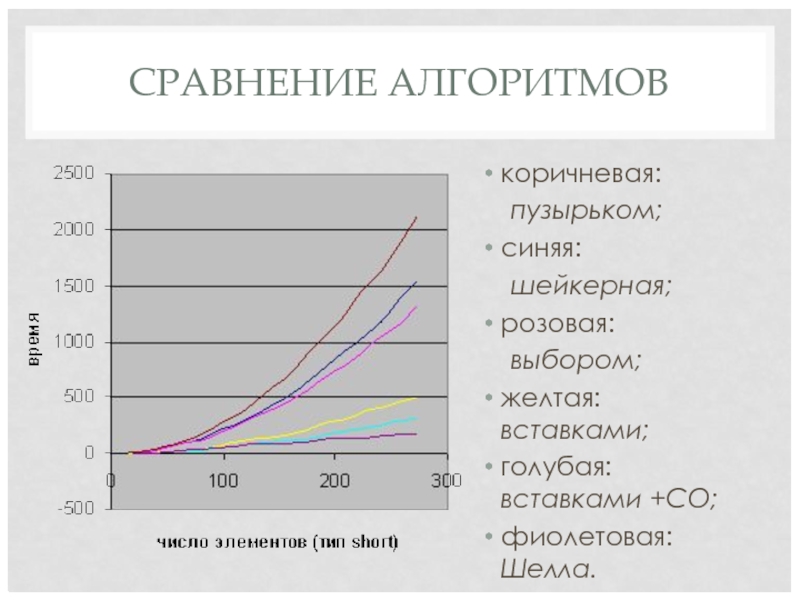
Слайд 39СРАВНЕНИЕ АЛГОРИТМОВ
коричневая:
пузырьком;
синяя:
шейкерная;
розовая:
выбором;
желтая: вставками;
голубая: вставками +СО;
фиолетовая: Шелла.
Слайд 40КОНТРОЛЬНАЯ РАБОТА N2
Алгоритмы сортировки реализовать в виде функций, возвращающих в качестве
результата характеристику трудоемкости алгоритма (количество сравнений).
Использовать файлы (fstream) для хранения промежуточных и окончательных результатов работы программы.
Получить трудоемкость для различных значений N=1000, 5000, 10000. Сравнить с теоретической оценкой. Нарисовать график.
Использовать файлы (fstream) для хранения промежуточных и окончательных результатов работы программы.
Получить трудоемкость для различных значений N=1000, 5000, 10000. Сравнить с теоретической оценкой. Нарисовать график.
