- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Представление информации в памяти компьютера презентация
Содержание
- 1. Представление информации в памяти компьютера
- 2. Представление чисел в памяти компьютера Для представления
- 3. Нумерация бит в двухбайтовом машинном слове
- 4. Представление текстовой информации в памяти компьютера
- 5. Представление текстовой информации в памяти компьютера
- 6. Представление текстовой информации в памяти компьютера
- 7. Представление текстовой информации в памяти компьютера
- 8. Представление чисел в памяти компьютера Смешанная двоично-десятичная
- 9. Представление чисел в памяти компьютера Формат с
- 10. Дополнительный код (ДК) Используется для
- 11. Принцип работы дополнительного кода на примере 10
- 12. Представление чисел в памяти компьютера (формат с
- 13. Пример 1. Записать число -40(10) в формате компьютера
- 14. Представление чисел в памяти компьютера (формат с
- 15. Представление чисел в памяти компьютера (формат с
- 16. Представление чисел в памяти компьютера (формат с
- 17. Любое действительное число можно записать в стандартном виде (иногда запись называют научной записью): M ⋅ 10p, где 1 ≤ M
- 18. Рассмотрим запись M ⋅ 10 p. Здесь: M
- 19. Представление чисел в памяти компьютера (формат с
- 20. Представление чисел в памяти компьютера (формат с
- 21. Представление чисел в памяти компьютера (формат с
- 22. Алгоритм получения представления действительного числа в памяти
- 23. Пример 1. Записать число –312,3125(10) в формате
- 24. Представление чисел в памяти компьютера (формат с
- 25. Представление чисел в памяти компьютера (формат с
- 26. Представление чисел в памяти компьютера (формат с
- 27. Представление чисел в памяти компьютера (формат с
- 28. Представление графической информации Рассмотрим растровую графику.
- 29. Представление графической информации Система кодирования цветной
- 30. Представление графической информации Качество графического изображения
- 31. Представление графической информации Число цветов, воспроизводимых
- 32. Представление звуковой информации Звуковая волна преобразуется
- 33. Представление звуковой информации Частота дискретизации –
- 34. Представление звуковой информации Разрядность регистра –
- 35. Представление звуковой информации Пример. Определить размер
Слайд 2Представление чисел в памяти компьютера
Для представления информации в памяти ЭВМ (как
Элементарная ячейка памяти ЭВМ имеет длину 8 бит (байт). Каждый байт имеет свой номер (его называют адресом).
Наибольшую последовательность бит, которую ЭВМ может обрабатывать как единое целое, называют машинным словом.
Слайд 3Нумерация бит в двухбайтовом машинном слове
Бит №15 считается старшим,
бит
Длина машинного слова зависит от разрядности процессора и может быть равной 16, 32 битам и т.д.
Слайд 4Представление текстовой информации в памяти компьютера
Символы текста (буквы, цифры, знаки)
Используя код из 1 бита, можно закодировать всего 2 разных символа.
Двухбитовых комбинаций может быть 4 (00; 01, 10, 11) т. е. 22.
Трехбитовых комбинаций – 8 (23).
Для кодирования 32 (25) различных символов достаточно 5 бит. Этот код использовался в работе телеграфа в 20-е годы ХХ века, вместо знаков препинания ставились ТЧК и ЗПТ.
Используя 7 бит, можно закодировать 128 символов (двоичный семибитовый код обмена информацией КОИ-7).
Слайд 5Представление текстовой информации в памяти компьютера
Оптимальное количество символов, которые используются
В 2-ой с.с.столько символов может быть закодировано последовательностью из 8 бит (28=256), т.е. 1 байтом.
Слайд 6Представление текстовой информации в памяти компьютера
Самая известная 8-битная кодировка –
Она состоит из 2-х частей: основная, одинаковая во всем мире (десятичные коды 0-127 – это управляющие коды, латинские буквы, знаки препинания, цифры) и расширенная (коды 128-255 – это буквы национального алфавита, символы псевдографики).
Первые 32 кода – это управляющие символы: возврат каретки, табуляция, отмена операции и т.п.
Слайд 7Представление текстовой информации в памяти компьютера
Помимо восьмиразрядной системы кодирования символьной
Такая система позволяет закодировать 216 = 65 536 различных символов, в том числе практически все алфавиты языков нашей планеты.
Расчет объема текстовой информации сводится к вычислению произведения количества символов в тексте на число разрядов двоичного кода, необходимого для кодирования одного символа.
Слайд 8Представление чисел в памяти компьютера
Смешанная двоично-десятичная «система счисления»
Каждый десятичный знак хранится
Десятичные цифры от 0 до 9 представляются двоичными числами от 0000 до 1001.
Например, упакованный десятичный формат для хранения целых чисел с 18-ю значащими цифрами занимает в памяти 10 байт (старший из которых знаковый), использует двоично-десятичную систему кодирования.
Слайд 9Представление чисел в памяти компьютера
Формат с фиксированной запятой
Используется для хранения целых
Старший бит (№15) может считаться знаковым. При этом если в нем хранится 0, то это +, если 1, то это – .
Цифровые разряды числа хранятся в дополнительном коде (ДК).
Слайд 10
Дополнительный код (ДК)
Используется для хранения отрицательных целых чисел и позволяет
Понятие дополнительного кода существует в любой системе счисления.
ДК получается путем вычитания данного отрицательного числа из минимального числа, в котором разрядов на один больше.
Рассмотрим принцип использования дополнительного кода на примере десятичной с.с.
Представление чисел в памяти компьютера (формат с фиксированной запятой)
Слайд 11Принцип работы дополнительного кода на примере 10 с.с.
Пусть необходимо вычислить: 8810
Такая привычная нам запись чисел - это прямой код (ПК) чисел.
Выполним вычитание через сложение чисел в ДК.
1) Переведем числа в ДК. Для числа 88 ДК совпадает с ПК. Так для всех чисел, которые больше 0. Для числа -64 (оно меньше 0) вычтем 64 из минимального трехразрядного числа (т.к. в числе 64 два разряда, то это 100):
100 – 64 = 36 – это ДК числа 64.
2) Теперь сложим ДК чисел: 88+36 = 124. Если отбросить старший разряд, то получится 24, что соответствует результату вычитания.
Слайд 12Представление чисел в памяти компьютера (формат с фиксированной запятой)
ДК для отрицательных
Слайд 13Пример 1. Записать число -40(10) в формате компьютера как целое со знаком.
Разрядность формата – 16 бит.
Решение.
1) Переводим 40(10) в двоичную систему счисления:
40(10) = 101000(2)
2) Получаем ПК числа в компьютерном формате. Для этого дополняем двоичную запись числа слева нулями так, чтобы стало 16 разрядов:
0000 0000 0010 1000
3) Получаем ДК, просматривая ПК справа налево
ПК: 0000 0000 0010 1000
ДК: 1111 1111 1101 1000
Это двоичная запись компьютерного представления числа -4010 в формате компьютера с фиксированной запятой разрядностью 16 бит.
Для более компактной записи используют шестнадцатеричный код: FFD8(16)
Представление чисел в памяти компьютера (формат с фиксированной запятой)
Слайд 14Представление чисел в памяти компьютера (формат с фиксированной запятой)
Пример 2. Записать
Решение.
1) Переводим 40(10) в двоичную систему счисления:
40(10) = 101000(2)
2) Получаем ПК числа в компьютерном формате. Для этого дополняем двоичную запись числа слева нулями так, чтобы стало 16 разрядов:
0000 0000 0010 1000
Полученный ПК совпадает с ДК, так как число положительное. Поэтому эта двоичная запись и есть компьютерное представление числа 4010 в формате компьютера с фиксированной запятой разрядностью 16 бит.
Для более компактной записи используют шестнадцатеричный код:
0028(16)
Здесь незначащие нули опускать нельзя, так как они хранятся в памяти компьютера.
Слайд 15Представление чисел в памяти компьютера (формат с фиксированной запятой)
Другой способ получения
Пример 3. Запишем ДК числа (–38), интерпретируя его как величину в формате с фиксированной запятой разрядностью 32 бита:
1) ПК числа 38: 0000 0000 0000 0000 0000 0000 0010 0110;
2) ОК числа -38 (здесь 0 заменён на 1, а 1 на 0): 1111 1111 1111 1111 1111 1111 1101 1001;
3) ДК получается прибавлением к ОК единицы: 1111 1111 1111 1111 1111 1111 1101 1010 или FFFFFFDB(16).
Слайд 16Представление чисел в памяти компьютера (формат с фиксированной запятой)
Пример 4. Дано
Решение.
1) Запишем двоичный код числа:
FFD4(16) = 1111 1111 1101 0100(2)
2) Выделим элементы формата:
3) Так как знаковый разряд равен 1 (это – ), то цифровые разряды записаны в ДК. Получим ПК по тому же правилу, по которому мы получали ДК:
ДК: 1111 1111 1101 0100
ПК: 0000 0000 0010 1100
4) Переводим ПК в 10 с.с.: 32+8+4 = 44(10)
5) Вспоминаем, что знак -. Поэтому ответ: -44(10)
Слайд 17Любое действительное число можно записать в стандартном виде (иногда запись называют
M ⋅ 10p, где 1 ≤ M < 10, p — целое.
Например, 120100000 = 1,201 ⋅ 108.
Поскольку каждая позиция десятичного числа отличается от соседней на степень числа 10, умножение на 10 эквивалентно сдвигу десятичной запятой на одну позицию вправо. Аналогично деление на 10 сдвигает десятичную запятую на позицию влево.
Поэтому пример можно продолжить:
120100000 = 1,201 ⋅ 108 = 0,1201 ⋅ 109 = 12,01 ⋅ 107….
Получается, что десятичная запятая «плавает» в числе и больше не помечает абсолютное место между целой и дробной частями.
Представление чисел в памяти компьютера (формат с плавающей запятой)
Слайд 18Рассмотрим запись M ⋅ 10 p.
Здесь: M – мантисса числа, p — порядок числа.
Чтобы сохранить максимальную точность, в памяти компьютера мантисса хранится в нормализованном виде. Это значит, что:
1 ≤ M < 2.
Такой способ хранения мантиссы с плавающей точкой подразумевает, что двоичная запятая находится на фиксированном месте: двоичная запятая следует после первой значащей двоичной цифры. Это значит, что в нормализованной мантиссе целая часть всегда равна 1. Тогда её значение лежит между единицей и двойкой.
Представление чисел в памяти компьютера (формат с плавающей запятой)
Слайд 19Представление чисел в памяти компьютера (формат с плавающей запятой)
Рассмотрим формат действительного
Место, отводимое для числа с плавающей точкой, делится на три поля: знак (старший бит), место для хранения порядка и место для хранения мантиссы. Для формата в 4 байта:
Слайд 20Представление чисел в памяти компьютера (формат с плавающей запятой)
Смещенный порядок –
Смещение выбирается так, чтобы минимальному значению порядка соответствовал ноль. Например, для формата 8 байт порядок занимает 11 бит и имеет диапазон от 2–1023 до 21023, поэтому смещение равно 1023(10) = 11 1111 1111(2) = 3FF(16).
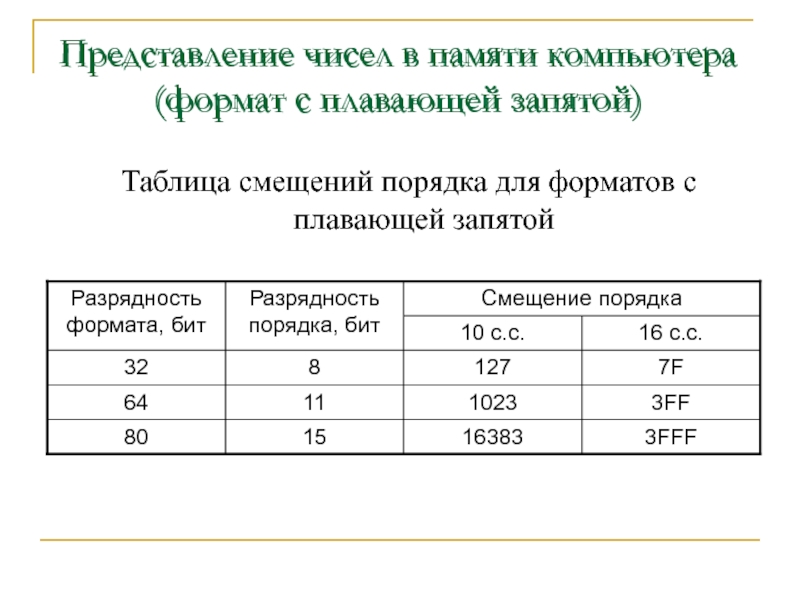
Слайд 21Представление чисел в памяти компьютера (формат с плавающей запятой)
Таблица смещений порядка
Представление чисел в памяти компьютера (формат с плавающей запятой)
Слайд 22Алгоритм получения представления действительного числа в памяти компьютера:
1) перевести модуль данного
2) нормализовать двоичное число, т.е. записать в виде M ⋅ 2p, где M — мантисса (ее целая часть равна 1) и p — порядок, записанный в десятичной системе счисления;
3) прибавить к порядку смещение и перевести смещенный порядок в двоичную систему счисления;
4) учитывая знак заданного числа (0 — положительное; 1 — отрицательное), выписать его представление в памяти компьютера. При этом из мантиссы выбросить целую часть, т.к. она всегда равна 1.
Представление чисел в памяти компьютера (формат с плавающей запятой)
Слайд 23Пример 1. Записать число –312,3125(10) в формате компьютера с плавающей запятой
Решение.
1) Двоичная запись модуля этого числа: 100111000,0101.
2) Нормализуем число, т.е. переносим запятую так, чтобы в целой части была одна 1.Имеем:
100111000,0101 = 1,001110000101 ⋅ 28.
3) Получаем смещенный порядок, добавляя к порядку смещение для 32-х битного формата (12710 или 7F16). Выполнять действия удобнее в 16-ой с.с.:
810 = 10002 = 816
816 + 7F16 = 8716 = 1000 01112 .
Представление чисел в памяти компьютера (формат с плавающей запятой)
Слайд 24Представление чисел в памяти компьютера (формат с плавающей запятой)
4) Выпишем элементы
Знак: 1 (т.к. число меньше 0)
Смещенный порядок: 1000 01112
Мантисса: 0011100001012 (целую часть не берем)
5) «Собираем» элементы формата:
1 10000111 001110000101 - всего 21 разряд, а нужно 32.
6) Добавляем еще 11 нулевых разрядов справа, т.к. это будут незначащие нули:
1100 0011 1001 1100 0010 1000 0000 00002
Это запись ответа в 2-ой с.с. Для более компактной записи используем 16-ю с.с.:
C39C2800
Слайд 25Представление чисел в памяти компьютера (формат с плавающей запятой)
Пример 2. Задано
Решение.
1) Двоичная запись этого числа:
1100 0001 0000 0100 0000 0000 0000 0000
2) Выделяем элементы формата:
Знак: 1 (т.е. число отрицательное)
Смещенный порядок: 1000 0010 или 8216
Мантисса: 000 0100 0000 0000 0000 0000
Слайд 26Представление чисел в памяти компьютера (формат с плавающей запятой)
3) Получаем порядок
8216 – 7F16 = 316
4) Получаем мантиссу – целая часть равна 1, а дробную часть берем из формата, отбрасывая незначащие нули:
1, 00001
5) Записываем двоичное число в нормальной форме:
-1,000012∙23
6) Порядок говорит о том, что запятую надо сдвинуть на 3 разряда вправо:
-1000,012 = - (8+1/4 ) = -8,2510
Слайд 27Представление чисел в памяти компьютера (формат с плавающей запятой)
Особенности формата с
Если при вычислениях с действительными числами результат выходит за пределы допустимого диапазона, то выполнение программы прерывается. Такое происходит, например, при делении на ноль, или на очень маленькое число, близкое к нулю.
Действительные числа, разрядность мантиссы которых превышает число разрядов, выделенных под мантиссу в памяти, представляются в компьютере приближенно (с “обрезанной” мантиссой). Например, рациональное десятичное число 0,1 в компьютере будет представлено приближенно (округленно), поскольку в двоичной системе счисления его мантисса имеет бесконечное число цифр. Следствием такой приближенности является погрешность машинных вычислений с вещественными числами.
Вычисления с вещественными числами компьютер выполняет приближенно. Погрешность таких вычислений называют погрешностью машинных вычислений.
Множество вещественных чисел, точно представимых в памяти компьютера в форме с плавающей точкой, является ограниченным и дискретным. Их количество можно вычислить.
Слайд 28Представление графической
информации
Рассмотрим растровую графику.
Для кодирования любого изображения его разбивают
Например, черно-белую картинку можно закодировать, используя два бита: 11 — белый цвет, 10 — светло-серый, 01 — темно-серый и 00 — черный цвет.
Для кодировки 256 различных цветов требуется 8 бит. Для кодирования полноцветных изображений в современных компьютерах для хранения цвета одной точки используется 3 байта.
Слайд 29Представление графической
информации
Система кодирования цветной графической информации RGB
(Red, Green, Blue)
Каждый
Белый цвет кодируется максимальной интенсивностью всех трех составляющих (255, 255, 255 или в 2-й с.с. 111111111, 11111111, 11111111). Черный цвет — отсутствие всех цветовых составляющих — (0,0,0). Красный цвет может быть темным — (120,0,0) или ярко-красным (255,0,0).
Система RGB обеспечивает однозначное определение 16,5 млн. различных цветов и оттенков (224).
Слайд 30Представление графической
информации
Качество графического изображения зависит также от количества точек (пикселей)
Расчет объема графической информации сводится к вычислению произведения количества точек в изображении на количество разрядов, необходимых для кодирования цвета одной точки.
Например, для цветной картинки размером 640 × 480, составленной из 256 цветов, требуется:
8 • 640 • 480 = 23 • 64 • 10 • 6 • 8 • 10 = 23 • 26 • 2 • 5 • 2 • 3 • 23 • 2 • 5 = 210 •5 •25 • 3 • 5 = 22 • 75 • 23 • 210 бит = 4•75 Кбайт = 300 Кбайт.
Слайд 31Представление графической
информации
Число цветов, воспроизводимых на экране (K), и число бит,
K=2N
Число бит N, отводимых под каждый пиксель называют битовой глубиной.
Слайд 32Представление звуковой
информации
Звуковая волна преобразуется в двоичный код с помощью звуковой
В процессе записи звука аудиоадаптер с определенным периодом измеряет амплитуду электрического тока и заносит в регистр двоичный код полученной величины.
Затем полученный код из регистра переписывается в оперативную память компьютера. Качество компьютерного звука определяется характеристиками аудиоадаптера: частотой дискретизации и разрядностью.
Слайд 33Представление звуковой
информации
Частота дискретизации – это количество измерений входного сигнала за
Одно измерение в секунду соответствует частоте 1 Гц.
1000 измерений в секунду соответствует частоте 1 кГц (килогерц).
Слайд 34Представление звуковой
информации
Разрядность регистра – это число бит в регистре аудиоадаптера.
Если разрядность 8, то при измерении входного сигнала можно получить 256 различных значений. Очевидно, чем больше разрядность аудиоадаптера, тем точнее воспроизводится звук.
Слайд 35Представление звуковой
информации
Пример. Определить размер V в байтах цифрового аудиофайла, время
Решение.
Формула: V = ν ∙ i ∙ t бит
22050∙10 ∙8 / 8 байт = 220500 байт