- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие информации. Свойства информации. Количество информации. Предмет информатики презентация
Содержание
- 1. Понятие информации. Свойства информации. Количество информации. Предмет информатики
- 2. Основные положения Информация – это продукт взаимодействия
- 3. СВОЙСТВА ИНФОРМАЦИИ: дуализм (двойственность); полнота; достоверность; доступность; актуальность
- 4. Первичная информация – это та, которая воспринимается
- 5. Понятие количества информации Свойство полноты информации негласно
- 6. Дуализм затрудняет определение количества информации. Существует несколько
- 7. Широко используются ещё более крупные производные единицы
- 8. Объемы информации необходимые для нормальной жизни современного
- 9. Информационные процессы Момент слияния данных и методов
- 10. Информация в жизни человечества В истории человечества
- 11. Третья информационная революция связывается с открытием электричества
- 12. Наше время отмечается как четвертая информационная революция.
- 13. Появляется, так называемое, информационное общество, где акцент
- 14. Развитие мировых информационных ресурсов позволило: повысить обоснованность
- 15. Предмет и структура информатики Термин информатика, как
- 16. методы реализации информационных процессов средствами вычислительной техники
- 17. состав, структура, общие принципы функционирования СВТ; используются
- 18. принципы управления СВТ. В разработке методов управления
- 19. Представление (кодирование) данных Типы данных: Числовые
- 20. Чтобы создать возможность работы с данными различных
- 21. Кодирование данных для обработки на компьютере (представление
- 22. В то же время, весьма просто реализуются
- 23. Предполагается, что данные располагаются в некоторых ячейках,
- 24. Итак, внутренняя азбука компьютера очень бедна,
- 25. Системы счисления Совокупность приемов записи и наименования
- 26. Позиционные системы счисления для записи чисел используют
- 27. В повседневной жизни мы пользуемся десятичной позиционной
- 28. в общем виде это запишется так
- 29. В информатике, большое значение имеет двоичная система
- 30. Это очень упростит конструкцию аппаратной части компьютера,
- 31. Восьмеричная система счисления имеет восемь цифр:
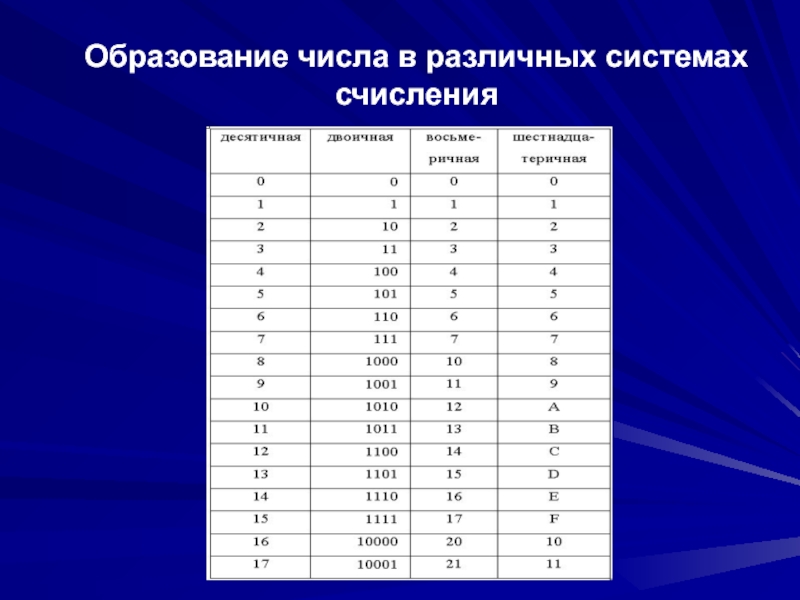
- 32. Образование числа в различных системах счисления
- 33. Преобразование чисел из одной системы счисления в
- 34. Преобразование из десятичной в прочие системы счисления
- 35. 231=115×21+1×20. Число 115 (такой двоичной цифры
- 36. 7÷2=3 остаток 1; 231=(((((3×2+1)×2+0)×2+0)×2+1)×2+1)×2+1=3×26+1×25+1×22+1×21+1×20 3÷2=1;
- 37. Читая частное и остатки от деления в
- 38. Для дробных чисел правило последовательного деления заменяется
- 39. Попутно заметим, что в десятичной системе счисления
- 40. Перевод из 2 ⬄ 8 и
- 41. Представление чисел в двоичном коде. Все данные
- 42. Целые числа Целые положительные числа от 0
- 43. Если нужны и отрицательные числа, то знак
- 44. Рассмотренный способ представления целых чисел называется прямым
- 45. В дополнительном коде хорошо реализуется арифметика, т.к.
- 46. Аналогично целые числа от 0 до 65536
- 47. Действительные числа Действительные числа в математике
- 48. Для представления действительных чисел, как очень маленьких,
- 49. Если мантисса находится в диапазоне 1/q≤|m|
- 50. Действительные числа в различных компьютер-ных системах записываются
- 51. Величина порядка представляется харак-теристикой (или смещенным порядком).
- 52. Чем больше разрядов отводится под запись мантиссы,
- 53. Понятие типа данных. Как уже говорилось, минимально
- 54. Для представления основных видов информации (числа целые,
- 55. Представление символьных и текстовых данных Тексты
- 56. Символы. Двоичное кодирование символьных данных производится
- 57. таблица CP 866 (ASCII 1981 г.
- 58. таблица CP 1251 (ASCII 1991 г.
- 59. Текстовые строки. Текстовая (символьная строка) -
- 60. Текстовые документы. Текстовые документы используются для
- 61. Представление звуковых данных в двоичном коде
- 62. Во время оцифровки сигнал дискретизируется по времени
- 63. Дискретизация по уровню, она еще называется квантованием,
- 64. Высокое качество воспроизведения получается в формате лазерного
- 65. Представление графических данных в двоичном коде
- 66. Модель RGB. Чтобы оцифровать цвет, прежде
- 67. Модель CMYK. В полиграфических системах напечатанный
- 68. Оцифровка изображения. изображение проецируется на светочувствительную матрицу
- 69. Очевидно, графические данные занимают очень большие объемы
- 70. Проблема сжатия информации Большие размеры файлов порождают
- 71. Структуры данных Доступность информации обеспечивается созданием структур
- 72. Табличная структура данных. Табличная структура данных -
- 73. Иерархическая структура. Нерегулярные данные, которые трудно
- 74. В линейной и табличной структурах доступ к
- 75. Хранение данных Здесь мы ответим на
- 76. Компьютерные системы хранят сотни тысяч файлов, доступ
- 77. Некоторые форматы файлов стандартизированы и поддерживаются многими
- 78. Программы начинают свою работу с чтения служебной
- 79. Подавляющей части пользователей практически ничего не нужно
- 80. Математические основы информатики. (Алгебра высказываний) Под простым
- 81. Логические операции Операцией отрицания A называют
- 82. Конъюнкцией двух высказываний A и
- 83. Дизъюнкцией двух высказываний A и
- 84. Импликацией двух высказываний A
- 85. Эквиваленцией двух высказываний A
- 86. Логические выражения С помощью логических
- 87. Зависимости между логическими операциями Операции не
- 88. (A∧B)∧C=A∧(B∧C) ассоциативный закон для конъюнкции
- 89. Одну и ту же зависимость между логическими
- 90. Мудрая мысль Любую логическую функцию можно привести к ДНФ и КНФ.
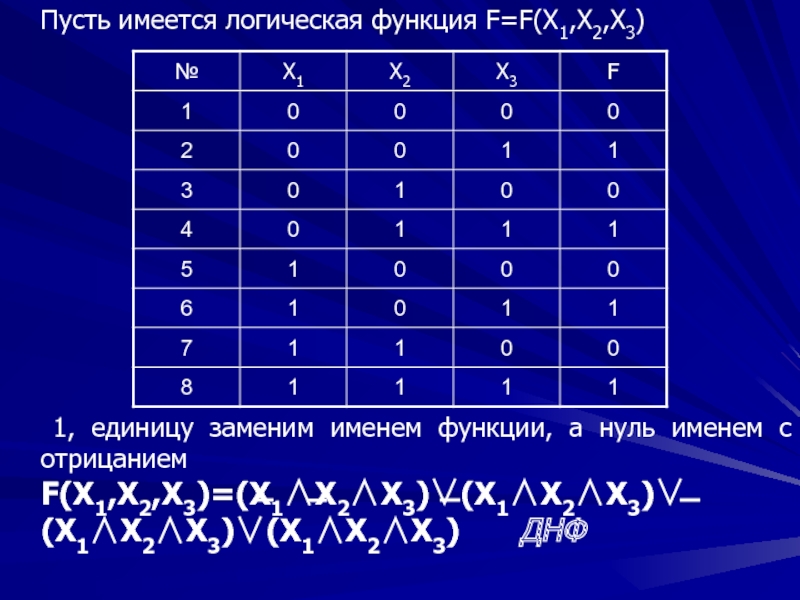
- 91. Пусть имеется логическая функция F=F(X1,X2,X3)
- 92. Еще более мудрая мысль Любое преобразование (обработка)
Слайд 2Основные положения
Информация – это продукт взаимодействия данных и адекватных методов.
Информация нужна
осмысления объекта или явления;
принятия решения (управление, созидание);
Слайд 4 Первичная информация – это та, которая воспринимается органами чувств (зрением, слухом,
она может существовать в виде: рисунков, фотографий, звуковых, вкусовых ощущений, запахов
На основе первичных данных сознанием могут быть построены вторичные абстрактные (смысловые, семантические) данные.
Вторичная может существовать в виде: в виде чисел, символов, текстов, чертежей, радиоволн, магнитных записей и т.д.
Слайд 5Понятие количества информации
Свойство полноты информации негласно предполагает, что имеется возможность измерять
Важнейшим результатом теории информации является вывод о том, что в определенных, весьма широких условиях, можно пренебрегая качественными особенностями информации, выразить её количество числом, а, следовательно, сравнивать количество информации, содержащейся в различных группах данных.
Слайд 6Дуализм затрудняет определение количества информации.
Существует несколько подходов к понятию количество информации.
Текстовый.
Шенона. За единицу информации принимается один бит (англ. bit — binary digit — двоичная цифра). Это количество информации, при котором неопределенность, уменьшается вдвое или другими словами, это ответ на вопрос, требующий односложного разрешения – да или нет.
Слайд 7Широко используются ещё более крупные производные единицы информации:
210 байт
220 байт = 1024 Кбайт =1 Мегабайт (Мбайт)
230 байт = 1024 Мбайт =1 Гигабайт (Гбайт)
240 байт = 1024 Гбайт = 1 Терабайт (Тбайт)
Слайд 8Объемы информации необходимые для нормальной жизни современного общества чрезвычайно велики
Человеческих возможностей
Слайд 9Информационные процессы
Момент слияния данных и методов называется информационным процессом.
Основные виды ИП:
Сбор
Передача данных – это процесс обмена данными.
Хранение данных – это поддержание данных в форме постоянно готовой к выдаче потребителю.
Обработка данных – это процесс преобразования информации от исходной ее формы до определенного результата.
Слайд 10Информация в жизни человечества
В истории человечества были четыре информационные революции
На первых
Письменные труды одного человека могли быть достоянием небольшого окружения создание печатного станка разрешило возникшее противоречие Эта веха в истории цивилизации характеризуется как вторая информационная революция (началась в XVI веке).
Слайд 11 Третья информационная революция связывается с открытием электричества и появлением (в конце
Слайд 12Наше время отмечается как четвертая информационная революция. Пользователями информации стали миллионы
Слайд 13 Появляется, так называемое, информационное общество, где акцент внимания и значимости смещается
Информационные ресурсы – это отдельные документы и массивы документов в информационных системах (библиотеках, архивах, фондах, банках данных, других информационных системах).
Слайд 14Развитие мировых информационных ресурсов позволило:
повысить обоснованность и оперативность принимаемых решений в
превратить деятельность по оказанию информационных услуг в глобальную человеческую деятельность;
сформировать мировой и внутригосударственный рынок информационных услуг;
Слайд 15Предмет и структура информатики
Термин информатика, как название науки, получил распространение с
Информатика – это наука изучающая:
методы реализации информационных процессов средствами вычислительной техники (СВТ);
состав, структуру, общие принципы функционирования СВТ;
принципы управления СВТ.
Кроме того, информатика – практическая наука, которая не только занимается описательным изучением перечисленных вопросов, но и во многих случаях предлагает способы их решения. В этом смысле информатика технологична и часто смыкается с информационными технологиями.
Слайд 16методы реализации информационных процессов средствами вычислительной техники (СВТ);
В этом разделе изучаются
представление различных типов данных (числа, символы, текст, звук, графика, видео и т.д.) в виде, удобном для обработки СВТ (кодирование данных), их форматы представления данных (предполагается, что одни и те же данные могут быть представлены разными способами);
теоретические проблемы сжатия данных;
структуры данных, т.е. способы хранения с целью удобного доступа к данным.
Слайд 17состав, структура, общие принципы функционирования СВТ;
используются научные положения из электроники, автоматики,
В этом разделе изучаются вопросы:
основы построения элементов цифровых устройств, принципы функционирования цифровых вычислительных устройств;
архитектура СВТ – основные принципы функционирования систем, предназначенных для автоматической обработки данных;
приборы и аппараты, составляющие аппаратную конфигурацию вычислительных систем;
приборы и аппараты, составляющие аппаратную конфигурацию компьютерных сетей.
Слайд 18принципы управления СВТ.
В разработке методов управления средствами вычислительной техники (средствами цифровой
В этом разделе изучаются вопросы:
средства взаимодействия аппаратного и программного обеспечения;
средства взаимодействия человека с аппаратным и программным обеспечением, объединяемые понятием интерфейс;
программное обеспечение СВТ (ПО);
Слайд 19Представление (кодирование) данных
Типы данных:
Числовые
Текстовые
Звуковые
Графические
Видео
Запахи
Вкусы
ДНК
И т.д.
Формы представления данных:
Непрерывная
Дискретная
СВТ (компьютеры)
Чтобы обрабаты-вать
Слайд 20Чтобы создать возможность работы с данными различных видов, необходимо унифицировать форму
Кодированием мы занимаемся довольно часто, например, человек мыслит весьма расплывчатыми понятиями, и, чтобы донести мысль от одного человека к другому, применяется язык. Язык – это система кодирования понятий. Чтобы записать слова языка, применяется, опять же, кодирование – азбука. Проблемами универсального кодирования занимаются различные области науки, техники, культуры. Вспомним, что чертежи, ноты, математические выкладки являются тоже некоторым кодированием различных информационных объектов.
Слайд 21Кодирование данных для обработки на компьютере (представление данных) в информатике имеет
Рассмотрим ее. Например, мы хотим проводить расчеты на компьютере. При этом нам придется закодировать цифры, которыми записаны числа. На первый взгляд, представляется вполне естественным кодировать цифру ноль состоянием электронной схемы, где напряжение на некотором элементе будет равно 0 вольт, цифру единица – 1 вольт, двойку – 2 вольт, и т.д. девятку – 9 вольт. Для записи каждого разряда числа в этом случае потребуется элемент электронной схемы, имеющий десять состояний. Однако, элементная база электронных схем имеет разброс параметров, что может привести к появлению напряжения, скажем, 3,5 вольт, а оно может быть истолковано и как тройка и как четверка, т.е. потребуется на уровне электронных схем объяснить компьютеру, где заканчивается тройка, а где начинается четверка. Кроме того, придется создавать весьма непростые электронные элементы для производства арифметических операций с числами, т.е. на схемном уровне должны быть созданы таблица умножения - 10х10=100 схем и таблица сложения – тоже 100 схем. Для электроники сороковых годов (время, когда появились первые вычислительные машины) это была непосильная задача. Еще сложнее выглядела бы задача обработки текстов, ведь русский алфавит содержит 33 буквы. Очевидно, такой путь построения вычислительных систем не состоятелен.
Слайд 22 В то же время, весьма просто реализуются электронные схемы с двумя
Слайд 23Предполагается, что данные располагаются в некоторых ячейках, представляющих упорядоченную совокупность из
Слайд 24Итак,
внутренняя азбука компьютера очень бедна, содержит всего два символа 0,
Слайд 25Системы счисления
Совокупность приемов записи и наименования чисел называется системой счисления.
Системы
Если для записи числа используется бесконечное множество символов, то система счисления называется непозиционной. Пример (достаточно плохой) – римская с.с.
Слайд 26 Позиционные системы счисления для записи чисел используют конечный набор символов, называемых
Количество цифр, используемых для записи числа, называется основанием системы счисления, в дальнейшем обозначим q.
По основанию именуется система счисления, например десятичная двоичная.
Слайд 27 В повседневной жизни мы пользуемся десятичной позиционной системой счисления, q=10, т.е.
0 1 2 3 4 5 6 7 8 9.
Число в позиционной системе счисления с основанием q может быть представлено в виде разложения по степеням q.
Например, в десятичной системе число
123,45(10)= 1*102+2*101+3*100+4*10-1+5*10-2
Слайд 28 в общем виде это запишется так
X(q)=xn-1qn-1+xn-2qn-2+…+x1q1+x0q0+
Здесь X(q) – запись числа в системе счисления с основанием q;
xi – цифры;
n – число разрядов целой части;
m– число разрядов дробной части.
Записывая слева направо цифры числа, мы получим закодированную запись числа в q-ичной системе счисления:
X(q)=xn-1xn-2x1x0 , x-1x-2x-3
Слайд 29 В информатике, большое значение имеет двоичная система счисления, q=2 т.к. таблица
Слайд 30 Это очень упростит конструкцию аппаратной части компьютера, но запись числа в
Что делает невозможным применение двоичной с.с. в повседневной жизни
Слайд 31 Восьмеричная система счисления имеет восемь цифр:
0 1 2 3 4
Шестнадцатеричная - шестнадцать:
0 1 2 3 4 5 6 7 8 9 A B C D E F.
Например, число 231, записанное в десятичной системе, запишется в двоичной, восьмеричной и шестнадцатеричной системах счисления так:
231(10)=11100111(2)=347(8)=E7(16)
Слайд 33Преобразование чисел из одной системы счисления в другую.
Преобразование чисел из произвольной
11100111(2)= 1×27+1×26+1×25+0×24+0×23+1×22+1×21+1×20=
128+64+32+4+2+1=231(10),
или
347(8)= 3×82+4×81+7×80=3×64+4×8+7=231(10)
Слайд 34 Преобразование из десятичной в прочие системы счисления проводится с помощью правил
Рассмотрим алгоритм на примере перевода десятичного числа 231 в двоичную систему, перевод из десятичной системы в любую q-ичную будет совершенно аналогичен.
Слайд 35231=115×21+1×20.
Число 115 (такой двоичной цифры нет) тоже может быть разделено
231=(57×2+1)×2+1= 57×22+1×11+1×20
аналогично продолжим процесс дальше
57÷2=28 остаток 1; 231=((28×2+1)×2+1)×2+1= 28×23+1×22+1×21+1×20
28÷2=14 остаток 0; 231=(((14×2+0)×2+1)×2+1)×2+1=14×24+1×22+1×21+1×20
14÷2=7 остаток 0; 231=((((7×2+0)×2+0)×2+1)×2+1)×2+1=7×25+1×22+1×21+1×20
Слайд 367÷2=3 остаток 1; 231=(((((3×2+1)×2+0)×2+0)×2+1)×2+1)×2+1=3×26+1×25+1×22+1×21+1×20
3÷2=1; остаток 1; далее процесс продолжать
231=((((((1×2+1)×2+1)×2+0)×2+0)×2+1)×2+1)×2+1=1×27+1×26+1×25+1×22+1×21+1×20
Таким образом, последовательное деление нацело позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа.
231 =1×27+1×26+1×25+0×24+0×23 +1×22+1×21+1×20 = 11100111(2)
Слайд 37 Читая частное и остатки от деления в порядке обратном получению, получим
Эти выкладки можно сократить, записав процесс в виде
алгоритма последовательного деления.
Слайд 38 Для дробных чисел правило последовательного деления заменяется правилом последовательного умножения.
0.8125(10) =1×2-1+1×2-2+1×2-4=0.1101(2).
Слайд 39 Попутно заметим, что в десятичной системе счисления правильная дробь переводится в
Аналогично, в двоичной системе счисления конечный вид получают дроби, где в знаменателе только степени двойки, т.е. большинство десятичных конечных дробей в двоичной системе счисления будут бесконечными периодическими дробями
Слайд 40Перевод из
2 ⬄ 8 и 2⬄16
Для того, чтобы перевести число
231(10)=11100111(2) =Е7(16)
запись числа в десятичной и шестнадцатеричной примерно одинаковы, но перевод чисел из 16 в 2 много проще.
Е
7
Слайд 41Представление чисел в двоичном коде.
Все данные содержатся в памяти компьютера в
Для каждого типа в отдельности создается собственный способ представления.
Слайд 42Целые числа
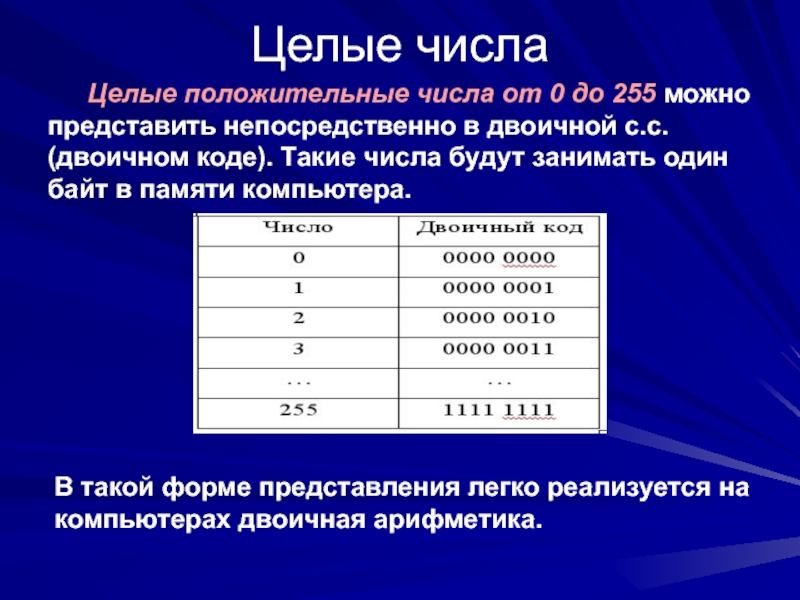
Целые положительные числа от 0 до 255 можно представить непосредственно
В такой форме представления легко реализуется на компьютерах двоичная арифметика.
Слайд 43 Если нужны и отрицательные числа, то знак числа может быть закодирован
причем двоичная арифметика будет несколько усложнена, т.к. в этом случае существуют два кода, изображающих число ноль 0000 0000 и 1000 0000, и в компьютерах на аппаратном уровне это потребуется предусмотреть.
Слайд 44 Рассмотренный способ представления целых чисел называется прямым кодом. Положение с отрицательными
Например, число –3 получит код
_ 1 0000 0000
0000 0011
1111 1101
Слайд 45В дополнительном коде хорошо реализуется арифметика, т.к. каждый последующий код получается
+ 0000 0101
1111 1101
1 0000 0010, т.е. отбрасывая подчеркнутый старший разряд получим 2
Слайд 46 Аналогично целые числа от 0 до 65536 и целые числа от
Слайд 47Действительные числа
Действительные числа в математике представ-ляются конечными или бесконечными дробями,
Однако в компьютерах числа хранятся в регист-рах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количест-вом разрядов.
Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в компьютер-ном представлении выступают как приближенные.
Слайд 48Для представления действительных чисел, как очень маленьких, так и очень больших,
X = m · qp, где
m — мантисса числа,
q – основание системы счисления,
p — целое число, называемое порядком.
Такой способ записи чисел называется представлением числа с плавающей точкой.
Т.е. число 1234.56 может быть записано в одном из видов
1234.56=123,456*101=12,3456*102 =1,23456*103 =0,123456*104
Слайд 49Если мантисса находится в диапазоне
1/q≤|m|
При фиксированном количестве разрядов, отведённых под мантиссу, в нормализованной форме обеспечивается запись максимального количества значащих цифр числа, т.е. максимальная точность.
Слайд 50 Действительные числа в различных компьютер-ных системах записываются по-разному, тем не менее,
Рассмотрим на примере 4 байтного числа.
32 31 30 24
Смещенный порядок
М а н т и с с а
Знак числа
23 22 21 2 1
Так как порядок может быть положительным или отрицательным, нужно решить проблему его знака.
Слайд 51 Величина порядка представляется харак-теристикой (или смещенным порядком). Для получения характеристики необходимо
Например, при использовании для хранения порядка семи бит, для хранения значений от –64 до +63 используется смещение 64.
Использование смещенной формы позволяет производить операции над порядками, как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.
Слайд 52Чем больше разрядов отводится под запись мантиссы, тем выше точность представления
Как и в случае целых чисел, в программных системах могут использоваться несколько типов данных, реализующих модель с плавающей точкой.
Слайд 53 Понятие типа данных. Как уже говорилось, минимально адресуемой единицей памяти является
Резюмируя вышесказанное, можно сделать вывод, что кроме задачи представления данных в двоичном коде, параллельно решается обратная задача – задача интерпретации кодов, т.е. как из кодов восстановить первоначальные данные.
Слайд 54 Для представления основных видов информации (числа целые, числа с плавающей запятой,
Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных. В дальнейшем для каждого типа данных будут определены и соответствующие ему операции обработки.
Слайд 55Представление символьных и текстовых данных
Тексты являются важнейшим источником информации. Для
Рассмотрим, как кодируются символы, символьные строки, текстовые документы.
Слайд 56Символы.
Двоичное кодирование символьных данных производится заданием кодовых таблиц, согласно которым
Обратная задача - интерпретация кодов осложнена тем, что в одном языке, как правило, существуют несколько кодовых таблиц. Это связано с тем, что кодовые таблицы разрабатывались в разных странах в разные времена.
Слайд 57таблица CP 866
(ASCII 1981 г. использовалась в MS-DOS. )
Для
Коды с 0 до 127 составляют базовую (основную) таблицу; коды со 128 по 255 расширенную (дополнительную) таблицу.
В основной таблице управляющие команды, спецсимволы, знаки арифметических действий и знаки препинания, цифры, латинские буквы - прописные и строчные.
Дополнительная таблица отдана национальным алфавитам и символам псевдографики.
Слайд 58таблица CP 1251 (ASCII 1991 г. использовалась в OS WINDOWS. )
базовая таблица осталась прежней, а расширенная - изменилась.
таблица Unicode 3.0
Код построен по 31 битной схеме, но используются только два байта для кодирования одного символа. Два байта 16 бит создает 216 = 65536 кодов, которые описывают цифры, буквы латинского и многих национальных алфавитов, спецсимволы, знаки арифметических операций и т.д.
Все текстовые документы в этой кодировке длинее вдвое, что сначала задерживало ее внедрение, но современный уровень технических средств допускает такую возможность.
Слайд 59Текстовые строки.
Текстовая (символьная строка) - это конечная последовательность символов. Это
Записывается в память символьная строка двумя способами: либо число, обозначающее длину текста, затем текст, либо текст затем разделитель строк.
Слайд 60Текстовые документы.
Текстовые документы используются для хранения и обмена данными/
Сплошной, не
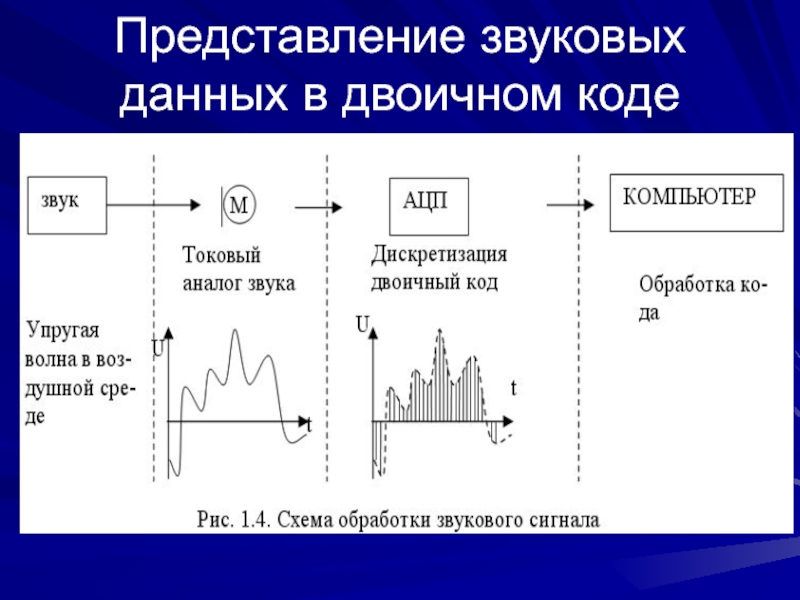
Слайд 62 Во время оцифровки сигнал дискретизируется по времени и по уровню.
Дискретизация
Слайд 63 Дискретизация по уровню, она еще называется квантованием, выполняется так: область изменения
ΔX=( Xmax- Xmin)/N
Точками X1,X2,…Xn. Xi=Xmin+ΔX⋅(i-1)
Возникают две задачи:
как часто по времени надо измерять сигнал,
с какой точностью надо измерять сигнал.
Ответ на первую задачу дает теорема Найквиста, которая утверждает, что, если сигнал оцифрован с частотой ν, то высшая «слышимая» частота будет не более ν/2. Вторая задача решается подбором числа уровней так, чтобы звук не имел высокого уровня шума и «электронного» оттенка звучания.
Слайд 64 Высокое качество воспроизведения получается в формате лазерного аудио диска при следующих
Таким образом, 1 сек. стерео звука займет
2байт*44100байт/сек*2кан*1сек=176 400 байт дисковой памяти. Качество звука при этом получается очень высоким.
Для телефонных переговоров удовлетворительное качество получается при частоте дискретизации 8 кгц и частоте квантования 255 уровней, т.е. 1 байт, при этом 1 сек звуковой записи займет на диске
1 байт*8000байт/сек*1сек=8000 байт
Слайд 65Представление графических данных в двоичном коде
Есть два основных способа представле-ния
Первый - графические объекты создают-ся как совокупности линий, векторов, точек - называется векторной графикой.
Второй - графические объекты форми-руются в виде множества точек (пикселей) разных цветов и разных яркостей, распреде-ленных по строкам и столбцам - называется растровой графикой.
Слайд 66Модель RGB.
Чтобы оцифровать цвет, прежде необходимо его измерить. Немецкий ученый
закон непрерывности - к любому цвету можно подобрать бесконечно близкий;
закон 3х-мерности - любой цвет может быть представлен комбинацией трех основных цветов;
закон аддитивности - цвет смеси зависит только от яркости составляющих.
За основные три цвета приняты красный (Red), зеленый (Green), синий (Blue). Эта модель (называется аддитивной) применяется для создания графических образов в устройствах, излучающих свет – мониторах, телевизорах.
Слайд 67Модель CMYK.
В полиграфических системах напечатанный на бумаге графический объект сам
голубой (Cyan=B+G), дополняющий красного;
пурпурный (Magenta=R+B) дополняющий зеленого;
желтый (Yellow=R+G) дополняющий синего.
Но т.к. цветные красители по отражающим свойствам не одинаковы, то для повышения контрастности применяется еще черный (blacK). Модель CMYK названа по первым буквам слов Cyan, Magenta, Yellow и последней букве слова blacK. Т.к. цвета вычитаются, модель называется субстрактивной.
Слайд 68Оцифровка изображения.
изображение проецируется на светочувствительную матрицу m строк и n столбцов,
Если для кодирования яркости каждой точки использовать по одному байту (8 бит) на каждый из трех цветов (всего 3*8=24 бита), то система обеспечит представление 224≈16.7 млн. распознаваемых цветов, что близко цветовосприятию человеческого зрения. Режим представления цветной графики двоичным кодом из 24 разрядов называется полноцветным или True Color.
Слайд 69Очевидно, графические данные занимают очень большие объемы на носителях. Например, экран
800×600×3= 1 440 000 байт.
В случае, когда не требуется высокое качество отображения цвета, применяют режим High Color, который кодирует одну точку растра двумя байтами (16 разрядов дают 216 ≈65.5 тысячи цветов).
Режим, который при кодировании одной точки растра использует один байт, называется индексным, в нем различаются 256 цветов. Этого не достаточно, чтобы передать весь диапазон цветов, код каждой точки при этом выражает собственно не цвет, а некоторый номер цвета (индекс) из таблицы цветов, называемой палитрой. Палитра должна прикладываться к файлам с графическими данными и используется при воспроизведении изображения.
Слайд 70Проблема сжатия информации
Большие размеры файлов порождают проблему сжатия информации. Теоретически доказано,
Проблема сжатия тесно связанная с моделями представления информации. Разработаны и применяется два типа алгоритмов сжатия: сжатие с изменением струк-туры данных (оно происходит без потери данных) и сжатие с частичной потерей данных.
Первые предусматривают восстановление данных точно в исходном виде.
Вторые не позволяют полностью восстановить оригинал и, потому применяются для хранения графики или звука, для текстов.
Слайд 71Структуры данных
Доступность информации обеспечивается созданием структур различают следующие структуры: линейные (списки),
Линейная структура.
Линейная структура данных (или список) - это упорядочен-ная структура, в которой адрес данного однозначно опреде-ляется его номером (индексом).
В линейной структуре необходим разделитель между элементами. Поиск осуществляется по разделителям.
Если элементы списка одной длины, структура называется вектором данных, разделители не требуются.
Слайд 72Табличная структура данных.
Табличная структура данных - это упорядоченная структура, в которой адрес
Если элементы располагаются в строчку, нужно внести два разделительных знака - разделительный знак между элементами строки и разделительный знак между строками.
Если элементы таблицы одной длины, структура называется матрицей данных, разделители в ней не требуются.
Таблица может быть и трехмерная, тогда три числа характеризуют положение элемента и требуются три типа разделителей, а может быть и n-мерная.
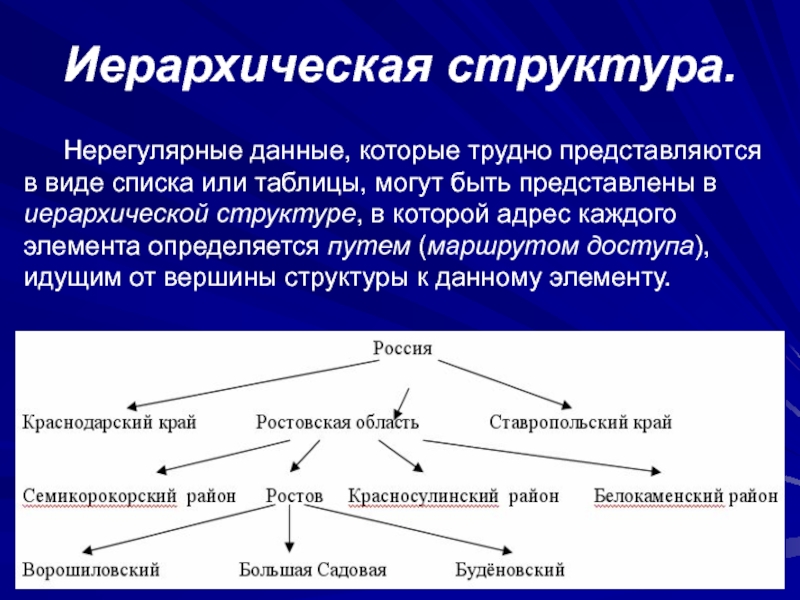
Слайд 73Иерархическая структура.
Нерегулярные данные, которые трудно представляются в виде списка или таблицы,
Слайд 74 В линейной и табличной структурах доступ к данным прост, но изменение
В иерархической структуре введение нового элемента не нарушает структуры дерева, недостатком ее является трудоемкость записи адреса и сложность поиска.
Реально существующие структуры часто представляют комбинации трех вышеописанных.
Слайд 75Хранение данных
Здесь мы ответим на вопрос как хранить громадные массивы
Единицей хранения информации является файл. Файл – это:
поименованная область на внешнем носителе произвольной длины,
содержащая данные различных типов, объединенные по какому либо признаку,
данные представлены в двоичном коде.
Слайд 76Компьютерные системы хранят сотни тысяч файлов, доступ к ним осуществляется с
Имя файла уникально (в рамках ФС) и несет в себе адресные функции в иерархической структуре реализуемой ФС.
Кроме того, имя может иметь расширение, в котором хранятся сведения о типе данных.
Физически файл является последовательностью байтов. Способ отображения, т.е. интерпретация определяется форматом файла.
Естественно, что для хранения различных видов информации, необходимо использовать по-разному устроенные файлы. Способ организации данных в файле (структура файла) называют его форматом.
Слайд 77Некоторые форматы файлов стандартизированы и поддерживаются многими приложениями (JPEG, MP3, AVI).
Структура файла может быть тривиальной. (Например, текст может сохраняться в виде последовательности байтов.) Но чаще вместе с данными приходится дополнительно сохранять служебную информацию.
Рассмотрим примеры.
Форматированный текст. Здесь нужно иметь два типа кодов: для кодирования самого текста, и для указания символов управляющих форматированием.
Таблица. Здесь также два типа кодов: для размера таблицы и для самих значений таблицы.
Слайд 78Программы начинают свою работу с чтения служебной информации и проверки, возможности
Современные программы, позволяют одновременно включать в файл данные разных видов, а это требует разработки очень сложных форматов. Например, работая с программой MS Word, мы можем включать в один документ текст, картинки, таблицы и др. Например, для хранения документов MS Office строятся так называемые структурированные хранилища — фактически целые файловые системы, спрятанные в едином с точки зрения пользователя файле.
Слайд 79Подавляющей части пользователей практически ничего не нужно знать о внутреннем устройстве
Попутно заметим, что наличие разных форматов для хранения данных одного и того же типа затрудняет переносимость их из среды одного приложения (программы) в среду другого. Проблема обычно решается использованием специальных программ, называемых конверторами.
Слайд 80Математические основы информатики. (Алгебра высказываний)
Под простым высказыванием понимается предло-жение, о котором
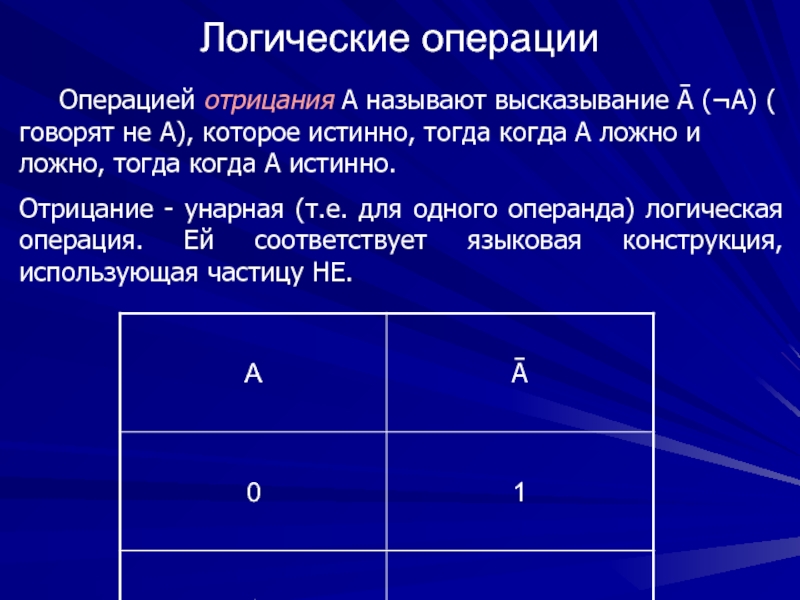
Слайд 81Логические операции
Операцией отрицания A называют высказывание Ā (¬A) ( говорят
Отрицание - унарная (т.е. для одного операнда) логическая операция. Ей соответствует языковая конструкция, использующая частицу НЕ.
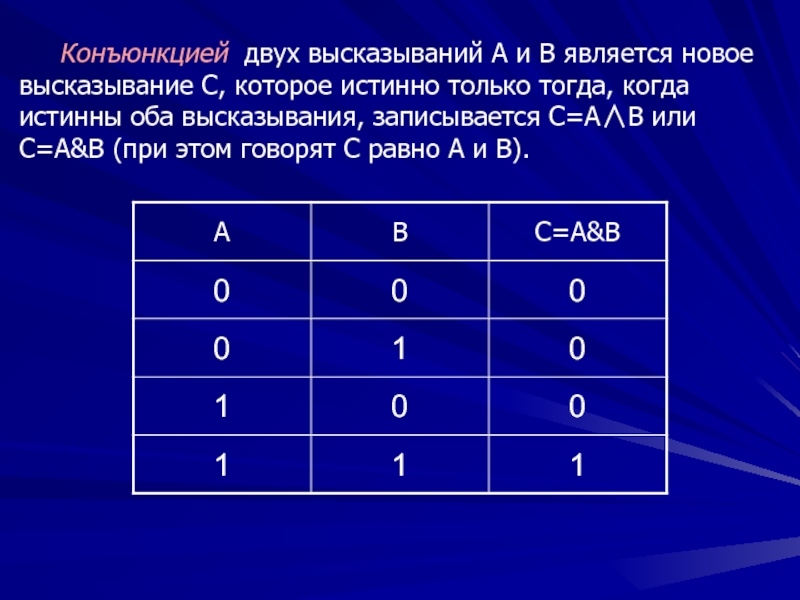
Слайд 82
Конъюнкцией двух высказываний A и B является новое высказывание C,
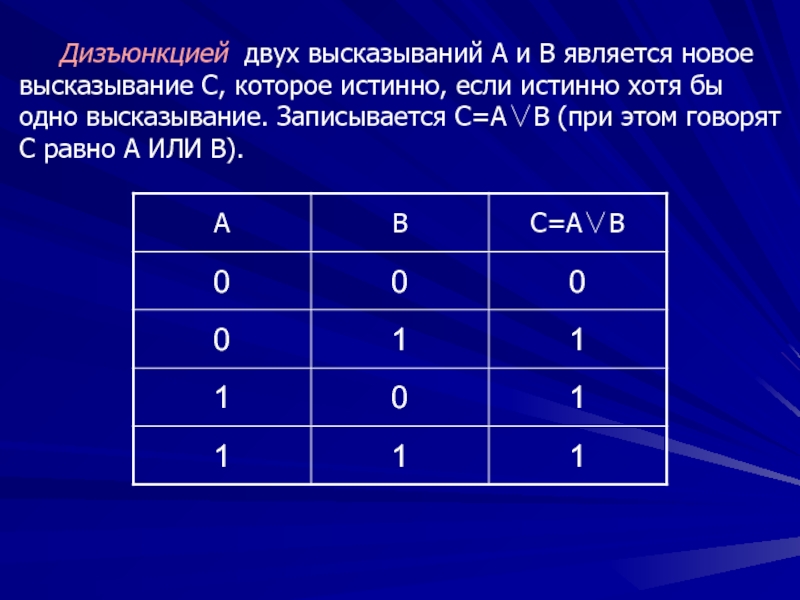
Слайд 83
Дизъюнкцией двух высказываний A и B является новое высказывание C,
Слайд 84
Импликацией двух высказываний A (называется посылкой) и B (называется
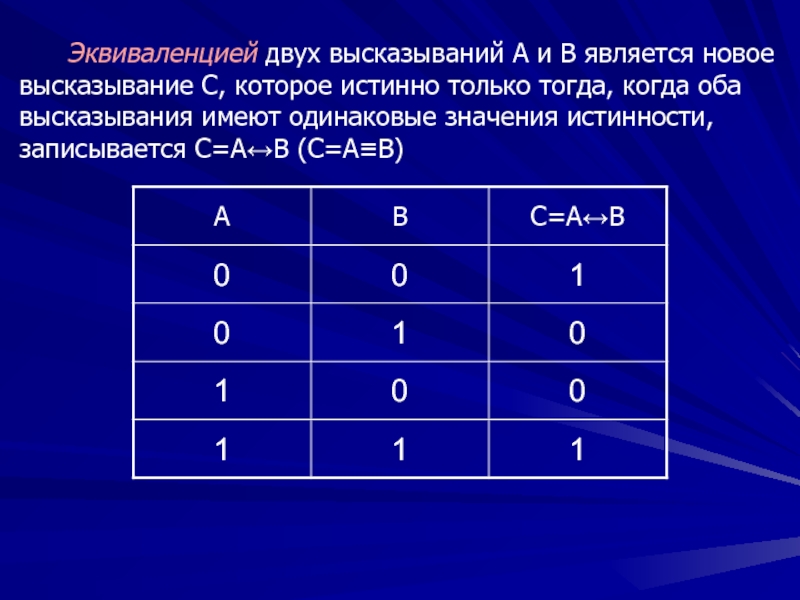
Слайд 85
Эквиваленцией двух высказываний A и B является новое высказывание
Слайд 86 Логические выражения
С помощью логических операций из простых высказываний (логических
Порядок операций:
операции в скобках
отрицание
конъюнкция и дизъюнкция слева на право
импликация, эквиваленция.
Слайд 87Зависимости между логическими операциями
Операции не являются независимыми; одни из них
A→B= Ā ∨B
A=A закон двойного отрицания.
A∧B=B∧A коммутативный закон для конъюнкции
A∨B=B∨A коммутативный закон для дизъюнкции
Слайд 88 (A∧B)∧C=A∧(B∧C) ассоциативный закон для конъюнкции (A∨B)∨C=A∨(B∨C) ассоциативный закон для
A∧(B∨C)=(A∧B)∨(A∧C) дистрибутивные законы A∨ (B∧C)=(A∨B)∧(A∨C)
(A∧B)=A∨B законы де Моргана
(A∨B)=A∧B
A∧1=A закон единицы для конъюнкции
A∧0=0 закон нуля для конъюнкции
A∨1=1 закон единицы для дизъюнкции
A∨0=A закон нуля для дизъюнкции
(A∧B)∧C=A∧(B∧C) ассоциативный закон для конъюнкции
(A∨B)∨C=A∨(B∨C) ассоциативный закон для дизъюнкции
A∧(B∨C)=(A∧B)∨(A∧C) дистрибутивные законы
A∨ (B∧C)=(A∨B)∧(A∨C)
(A∧B)=A∨B законы де Моргана
(A∨B)=A∧B
A∧1=A закон единицы для конъюнкции
A∧0=0 закон нуля для конъюнкции
A∨1=1 закон единицы для дизъюнкции
A∨0=A закон нуля для дизъюнкции
Слайд 89 Одну и ту же зависимость между логическими переменными можно выразить различными
A1∨A2∨…∨An, где каждое из составляющих есть конъюнкция простых высказываний и их отрицаний, например
B=(A1∧A2∧A3)∨(A1∧A2)
Вторая – конъюнктивная нормальная форма (КНФ), имеет вид
A1∧A2∧…∧An, где каждое из составляющих есть дизъюнкция простых высказываний и их отрицаний, например
B=(A1∨A2∨A3)∧(A2∧A3)∧( A1∨A2∨A3)
Слайд 91Пусть имеется логическая функция F=F(X1,X2,X3)
1, единицу заменим именем функции, а
Слайд 92Еще более мудрая мысль
Любое преобразование (обработка) двоич-ной информации может быть представлена
А каждую функцию можно представить в КНФ или ДНФ.
Если электронное устройство, способно моделировать двоичный сигнал и может выпол-нить отрицание, конъюнкцию и дизъюнкцию двух сигналов, то такое устройство может обрабаты-вать информацию.
Если же добавить еще устройство хранящее информацию, то возможна работа по программе.