- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы криптографической защиты информации. (Тема 3.8) презентация
Содержание
- 1. Основы криптографической защиты информации. (Тема 3.8)
- 2. Занятие 8
- 3. Криптография – наука о шифрах.
- 4. Криптография была поставлена на научную
- 5. Криптография Криптография в переводе с греческого языка означает тайнопись
- 6. Классическая задача криптографии Классической задачей криптографии
- 7. Основные понятия открытая информация
- 8. Основные понятия конфиденциальная, секретная, приватная информация, информация с ограниченным доступом
- 9. Важная информация Информация, причинение ущерба которой может
- 10. Основные задачи защиты информации обеспечение конфиденциальности информации
- 11. Основные задачи защиты информации обеспечение целостности информации
- 12. Основные задачи защиты информации обеспечение достоверности информации
- 13. Основные задачи защиты информации обеспечение оперативности доступа
- 14. Основные задачи защиты информации обеспечение юридической значимости
- 15. Основные задачи защиты информации обеспечение неотслеживаемости действий
- 16. Основу обеспечения информационной безопасности в информационно-телекоммуникационных системах составляют криптографические методы и средства защиты информации.
- 17. Криптографические методы защиты информации и ресурсов
- 18. Варианты защиты
- 19. Система засекреченной связи Система засекреченной связи –
- 20. Основные термины Зашифрование – процесс криптографического преобразования
- 21. Система засекреченной связи Система засекреченной связи —
- 22. Система засекреченной связи Отображения должны обладать свойством
- 23. Система засекреченной связи Зашифрование Расшифрование Открытый текст
- 24. Основные термины Выбор конкретного типа преобразования определяется
- 25. Работа системы засекреченной связи Из ключевого пространства
- 26. Работа системы засекреченной связи Зашифрованное сообщение С
- 27. Формула вычисления числа необходимых ключей N=(время жизни
- 28. Криптостойкость
- 29. Криптостойкость Стойкость алгоритма шифрования (криптостойкость) — способность противостоять всем возможным атакам против него
- 30. Раскрытие системы засекреченной связи (алгоритма шифрования) полное
- 31. Раскрытие системы засекреченной связи (алгоритма шифрования) нахождение
- 32. Атаки на криптоалгоритмы Атака с известным шифртекстом
- 33. Атаки на криптоалгоритмы Атака с известным открытым
- 34. Атаки на криптоалгоритмы Атака с выбором открытого
- 35. Криптостойкость Стойким считается алгоритм, в котором перехват
- 36. Криптостойкость Криптограмма1 Ключn …
- 37. Криптостойкость Криптограмма1 КлючK От. текст1К
- 38. Криптостойкость Стойким считается алгоритм, который для своего
- 39. Время жизни информации
- 40. Типы алгоритмов шифрования
- 41. Типы алгоритмов шифрования В криптографии существуют только
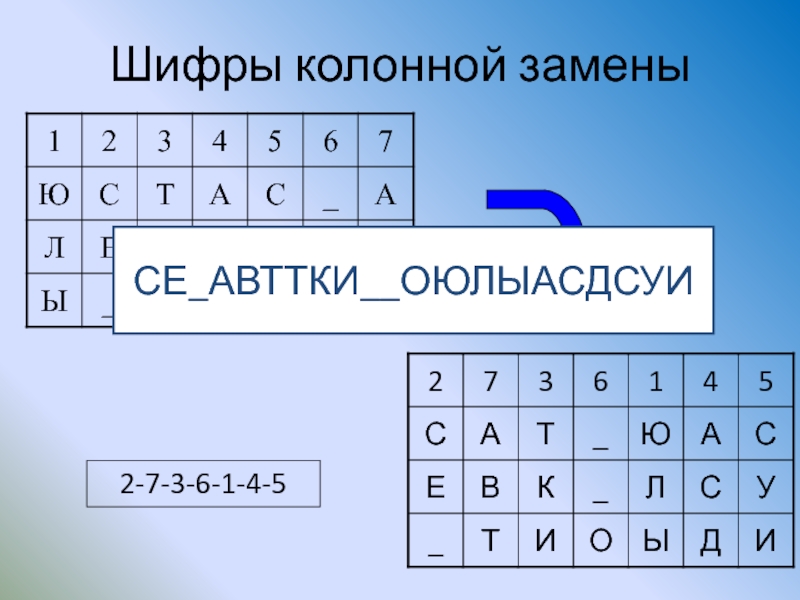
- 42. Шифры колонной замены 2-7-3-6-1-4-5 СЕ_АВТТКИ__ОЮЛЫАСДСУИ
- 43. Перестановки КРЕПИ ДРУЖБУ КПДЖРИРБЕ УУ УБЖУРД ИПЕРК РКПЕ ИРДЖУУБ
- 44. Шифры замены В шифрах замены один символ
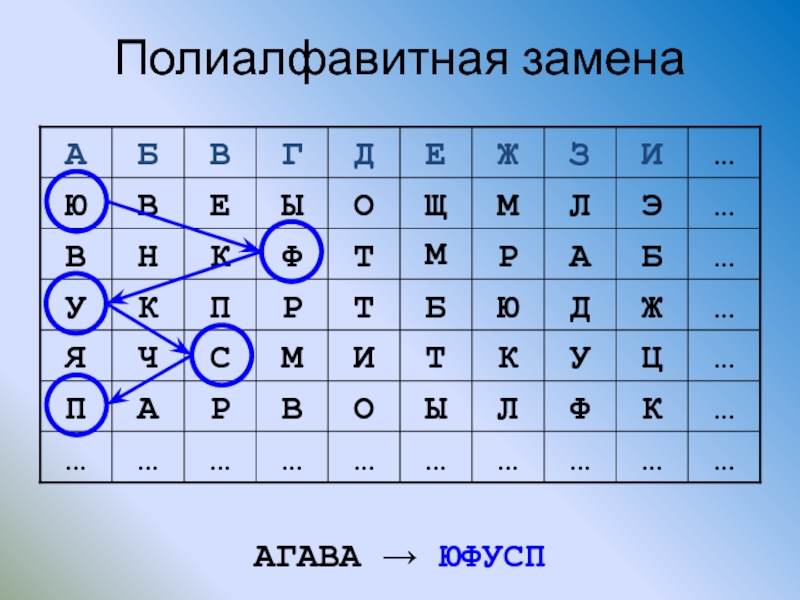
- 45. Полиалфавитная замена АГАВА → ЮФУСП
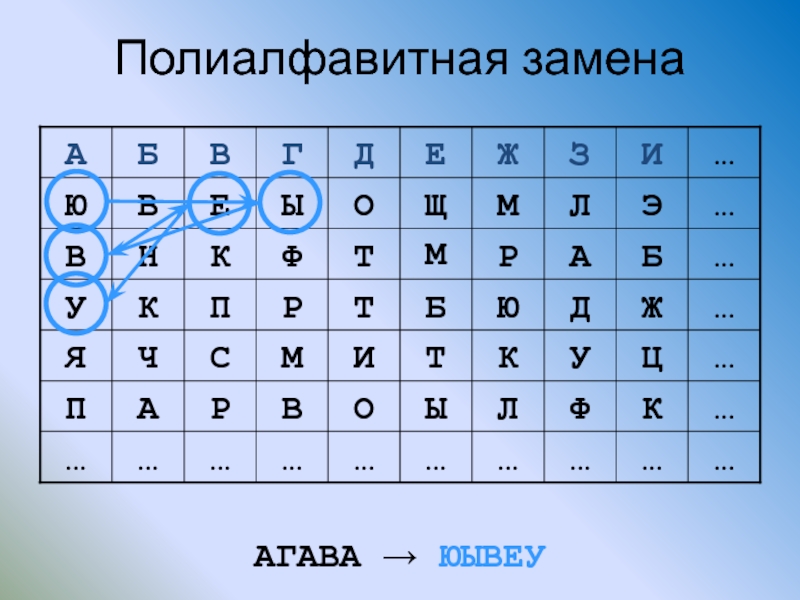
- 46. Полиалфавитная замена АГАВА → ЮЫВЕУ
- 47. Типы алгоритмов шифрования В блочных шифрах открытый
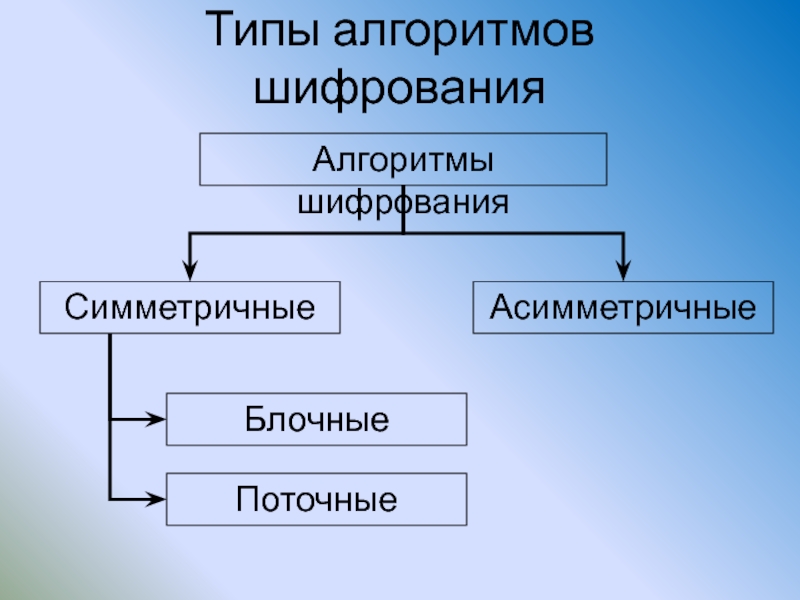
- 48. Типы алгоритмов шифрования Алгоритмы шифрования Симметричные Асимметричные Блочные Поточные
- 49. Система засекреченной связи Зашифрование Расшифрование Открытый текст
- 50. Типы алгоритмов шифрования Классическая схема: ключи зашифрования
- 51. Абсолютно стойкие шифры
- 52. Необходимое условие абсолютной стойкости шифра по К.Шеннону
- 53. Правило Керкхоффа «Компрометация системы не должна причинять
- 54. Правило Керкхоффа Шифр – параметризованный алгоритм, состоящий
- 55. Преимущества разглашение конкретного шифра (алгоритма и ключа)
- 56. Преимущества ключи можно отчуждать от остальных компонентов системы шифрования – хранить отдельно от реализации алгоритма;
- 57. Преимущества появляется возможность для точной оценки «степени
- 58. Абсолютно стойкие шифры Абсолютно стойкие или совершенные
- 59. Условие абсолютной стойкости для шифров удовлетворяющих
- 60. Причины осуществления успешных атак на алгоритмы шифрования
- 61. Методы, затрудняющие криптоанализ Рассеивание (Diffusion). Влияние одного
- 62. Абсолютно стойкие шифры шифр Вернама
- 63. Абсолютно стойкие шифры
- 64. Абсолютно стойкие шифры
- 65. Абсолютно стойкие шифры
- 66. Абсолютно стойкие шифры
- 67. Абсолютно стойкие шифры
- 68. Абсолютно стойкие шифры
- 69. Абсолютно стойкие шифры
- 70. Абсолютно стойкие шифры
- 71. Симметричные алгоритмы
- 72. Симметричные алгоритмы Простейшие: шифр Вернама, Цезаря, Виженера,
- 73. АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ_
- 74. Ю→А С→Т Т→Ц А→П С→Я _→И А→Е Л→С Е→Ш К→Ш С→Т У→Д Шифр Виженера сообщение:
- 75. Шифр Плэйфера Ключ: криптография ПР ИМ ЕР
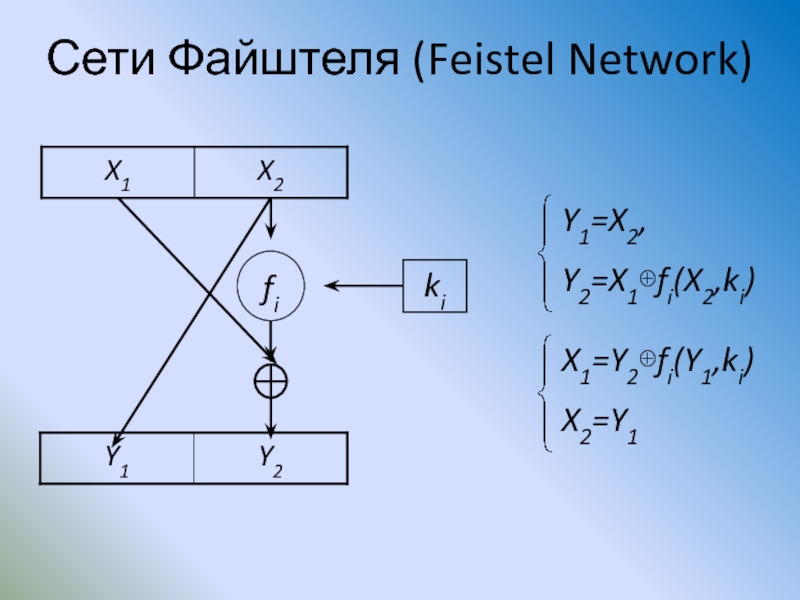
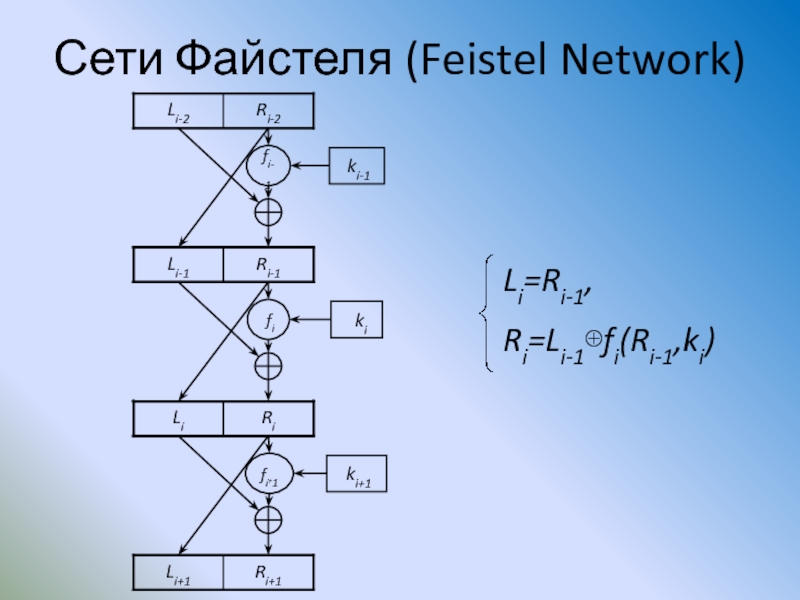
- 76. Сети Файштеля (Feistel Network)
- 77. Сети Файстеля (Feistel Network) Ri-2 Li-2 fi-1
- 78. DES Data Encryption Standard. Разработан в 1977
- 79. Шифрование с открытым ключом Alice (открытый ключ
- 80. DES Доработка: TripleDES Ключ 168 бит:
- 81. ГОСТ 28147-89 Системы обработки информации. Защита криптографическая.
- 82. ГОСТ 28147-89 4 режима работы: простая замена гаммирование гаммирование с обратной связью выработка имитовставки
- 83. ГОСТ 28147-89: Структура
- 84. Образующая функция ГОСТ 28147-89 32 компоненты
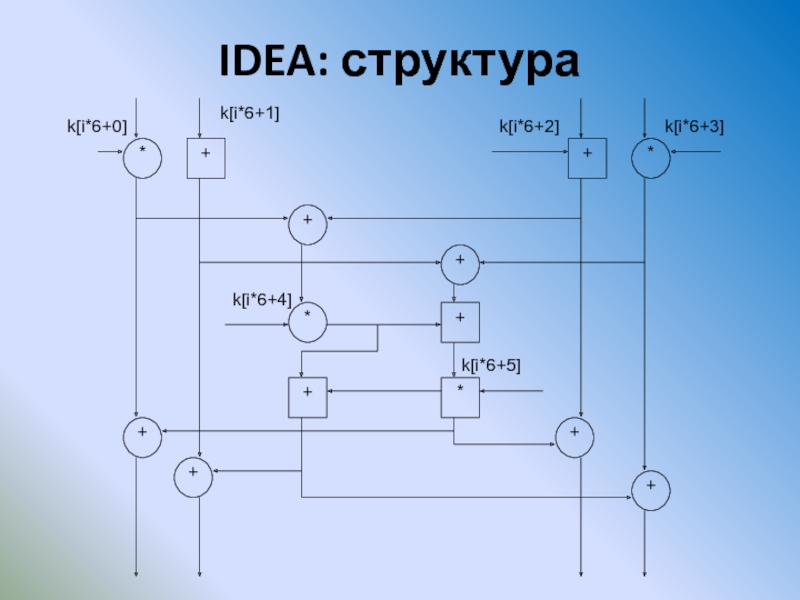
- 85. IDEA: структура
- 86. Алгоритм IDEA IDEA: расширение ключа k[0]...k[7]=key
- 87. Oсновные термины Гамма шифра — псевдослучайная двоичная
- 88. Простая замена Накопитель N2 Накопитель N1 Блок открытого текста
- 89. Простая замена Накопитель N2 Накопитель N1 Блок открытого текста +
- 90. Простая замена Накопитель N2 Накопитель N1 Блок открытого текста Таблица подстановок + Регистр сдвига
- 91. Порядок использования ключей Шифрование: Раунды с 1-го
- 92. Гаммирование Накопитель N2 Накопитель N1 Синхропосылка S Таблица подстановок + Регистр сдвига
- 93. Гаммирование Накопитель N2 Накопитель N1 E (S) Накопитель N4 Накопитель N3
- 94. Гаммирование Накопитель N2 Накопитель N1 E (S)
- 95. Гаммирование Накопитель N2 Накопитель N1 Накопитель N4 Накопитель N3
- 96. Гаммирование Накопитель N2 Накопитель N1 Гамма шифра
- 97. Гаммирование Накопитель N2 Накопитель N1 Гамма шифра Открытый текст2 Открытый текст1 Шифртекст Выход
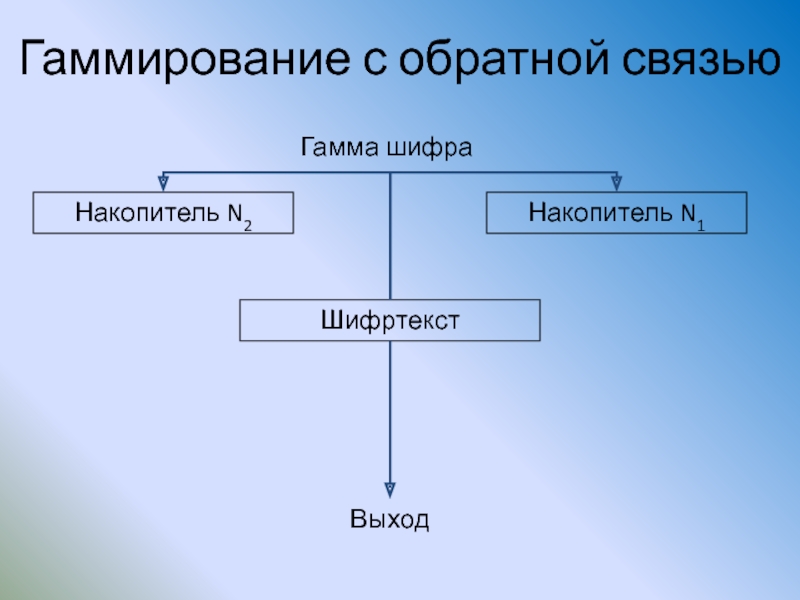
- 98. Гаммирование с обратной связью Накопитель N2 Накопитель N1 Шифртекст Выход Гамма шифра
- 99. Основные термины Имитозащита — защита системы шифрованной
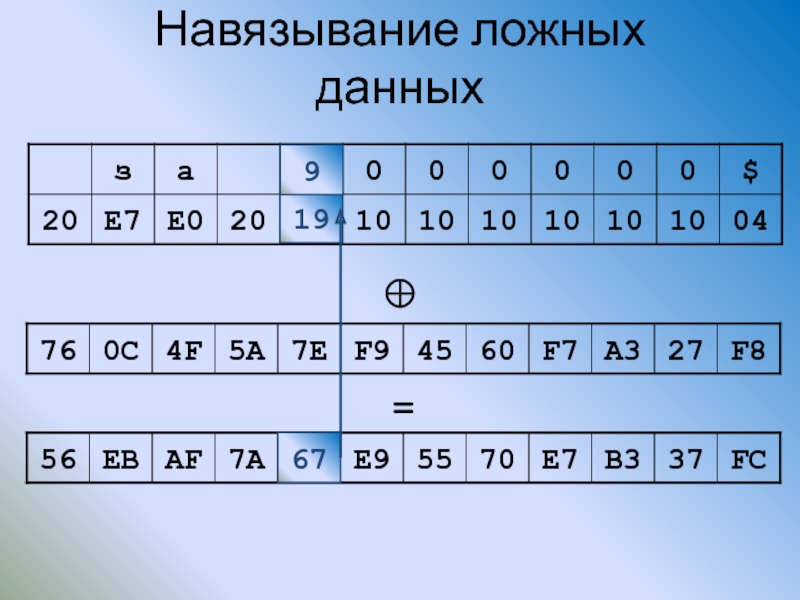
- 100. Навязывание ложных данных 67
- 101. Выработка имитовставки Накопитель N2 Накопитель N1 Открытый текст Таблица подстановок + Регистр сдвига
- 102. Выработка имитовставки Накопитель N2 Накопитель N1 Открытый
- 103. ГОСТ 28147-89 Достоинства: на сегодняшний день не
- 104. AES Advanced Encryption Standard (Rijndael) Авторы: Йон
- 105. AES Каждый блок кодируемых данных представляется в
- 106. Табличная подстановка
- 107. Сдвиг строк нет сдвига >> 1 >> 2 >> 3
- 108. Перемешивание
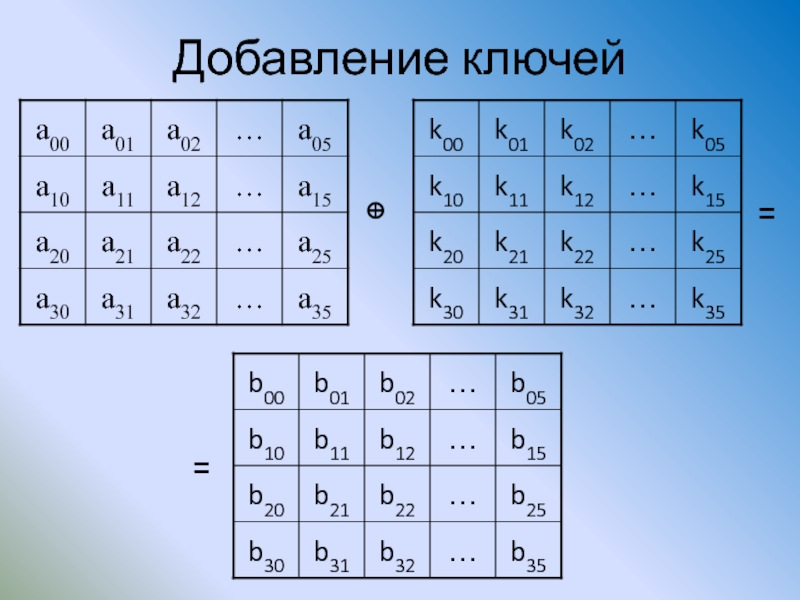
- 109. Добавление ключей
- 110. AES Достоинства: эффективен как на 8-битных так
- 111. Зашифрование и расшифрование осуществляется, например, путем сложения
- 112. Поточные алгоритмы. Проблемы Стойкость зависит от обеспечения
- 113. Методы обеспечения синхронизации самосинхронизирующиеся шифраторы (очередной символ
- 114. Методы обеспечения синхронизации синхронные шифраторы (осуществляют синхронизацию
- 115. Скремблеры Единственная операция: сложение по модулю 2
- 116. Скремблеры Основная проблема: зацикливание Зацикливание неустранимо:
- 117. Асимметричные алгоритмы
- 118. Асимметричные алгоритмы Уитфрид Диффи, Мартин Хеллман: «Новые
- 119. Односторонние функции Необратимые или односторонние функции: y=f(x)
- 120. Проблема На сегодняшний день теоретически не доказано
- 121. Асимметричные алгоритмы Односторонние функции с секретом: fz(x):
- 122. RSA Авторы: Rivest, Shamir, Adleman Обнародован в
- 123. Пример 16444757698990888364317098853 – простое? 189435747774163 • 878634363654631 = 16444757698990888364317098853
- 124. Генерация ключей Выбираются два очень больших
- 125. Генерация ключей Выбирается достаточно большое
- 126. Секретным ключом является пара чисел (n, d),
- 127. RSA Секретным ключом является пара чисел (n,
- 128. Выбираем: p = 3; q = 11
- 129. Сообщение: ПОРА (04h, 03h, 05h, 02h) 47
- 130. Шифртекст: (16, 9, 14, 29) или (10h, 09h, 0Еh,
- 131. Проблемы RSA Некорректный выбор p и q Наличие нешифруемых блоков Критичность к некоторым видам атак
- 132. Основные разновидности асимметричных алгоритмов RSA (разложение на множители) Эль-Гамаля (дискретное логарифмирование) на основе эллиптических кривых
- 133. Хэш-функции
- 134. Хэш-функции Хэш-функции — функции, отображающие последовательность произвольной
- 135. Хэш-функции Основные требования: отсутствие коллизий, т.е. невозможность
- 136. Хэш-функции SHA (Security Hash Algorithm) Разработчики: NIST
- 137. Электронно-цифровая подпись
- 138. ЭЦП Цель подписи: гарантирование истинности письма путем
- 139. Схемы построения ЭЦП Шифрование электронного документа на
- 140. Схемы построения ЭЦП Использование асимметричных алгоритмов шифрования Сообщение Антон Борис Владимир
- 141. Схемы построения ЭЦП На основе хэш-функции при помощи асимметричного алгоритма Сообщение Антон Борис Владимир
- 142. Схемы построения ЭЦП На основе хэш-функции при
- 143. Нарушения в процессе информационного обмена, обнаруживаемые при помощи ЭЦП
- 144. Отказ (ренегатство) Сообщение А заявляет, что он
- 145. Модификация Сообщение Б, приняв сообщение, изменяет
- 146. Подделка Сообщение Б формирует сообщение и
- 147. Навязывание Сообщение Злоумышленник В перехватывает обмен
- 148. Имитация Сообщение Злоумышленник В пытается отправлять
- 149. Основные достоинства и недостатки «классических» (симметричных) и
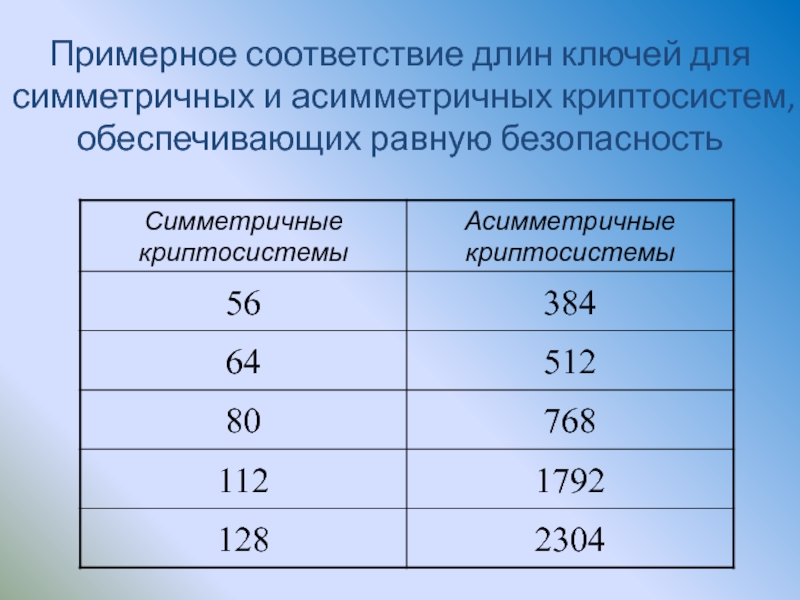
- 150. Примерное соответствие длин ключей для симметричных и асимметричных криптосистем, обеспечивающих равную безопасность
- 151. «Гибридная» схема криптографической защиты Генерация сеансового ключа
- 152. «Гибридная» схема криптографической защиты Сообщение Сообщение Симметричный ключ
- 153. Вероятностные шифры Одним из перспективных способов повышения
- 154. Вероятностные шифры Сообщение: ЮСТАС АЛЕКСУ А →
Слайд 3Криптография – наука о шифрах.
Криптография базируется на самых последних
Слайд 4 Криптография была поставлена на научную основу во многом благодаря
Слайд 6Классическая задача криптографии
Классической задачей криптографии является обратимое преобразование некоторого понятного
Слайд 8Основные понятия
конфиденциальная, секретная, приватная информация, информация с ограниченным доступом
Слайд 9Важная информация
Информация, причинение ущерба которой может повлечь за собой существенные материальные,
Слайд 10Основные задачи защиты информации
обеспечение конфиденциальности информации
Конфиденциальность – свойство информации быть доступной
Слайд 11Основные задачи защиты информации
обеспечение целостности информации
Под целостностью понимается свойство информации
Слайд 12Основные задачи защиты информации
обеспечение достоверности информации
Достоверность – отсутствие случайных ошибок
Слайд 13Основные задачи защиты информации
обеспечение оперативности доступа к информации
Под оперативностью доступа
Слайд 14Основные задачи защиты информации
обеспечение юридической значимости информации, представленной в виде электронного
Юридическая значимость означает, что документ обладает юридической силой.
Необходимо: повсеместное принятие некоторых атрибутов информации, выражающих ее способность быть юридически значимой
Слайд 15Основные задачи защиты информации
обеспечение неотслеживаемости действий клиента
Неотслеживаемость – способность совершать
Слайд 16Основу обеспечения информационной безопасности в информационно-телекоммуникационных системах составляют криптографические методы и средства защиты
Слайд 17Криптографические методы защиты информации и ресурсов
шифрование всего информационного трафика
криптографическая
защита трафика средствами имитозащиты и ЭЦП
шифрование данных, представленных в виде файлов либо хранящихся в базе данных
контроль целостности
обеспечение юридической значимости документов
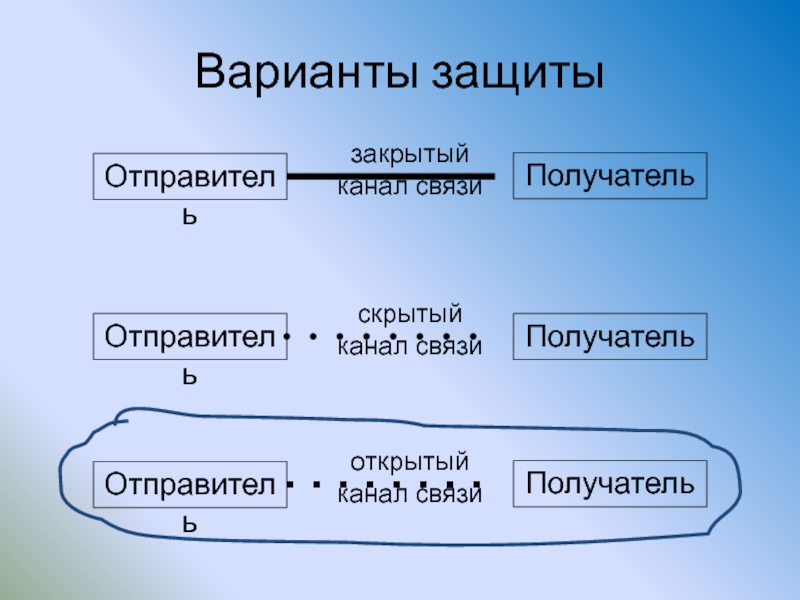
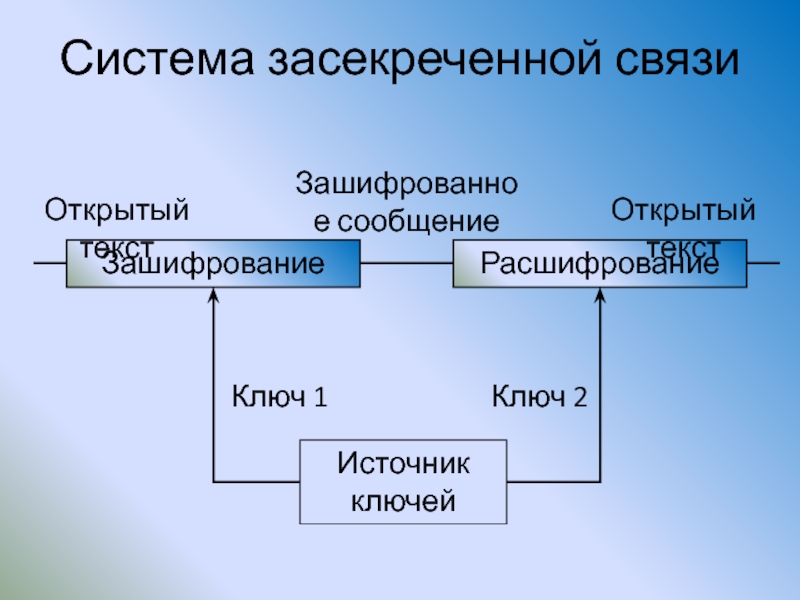
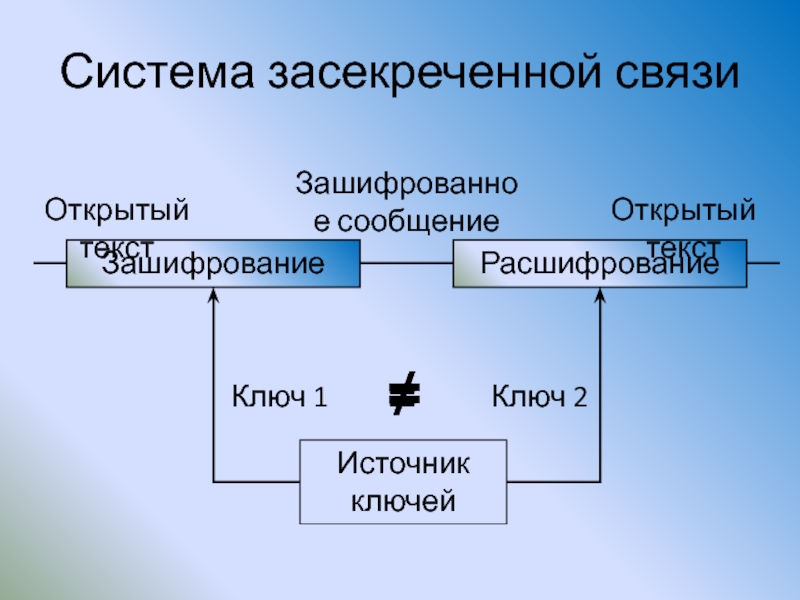
Слайд 19Система засекреченной связи
Система засекреченной связи – это система передачи информации, в
Слайд 20Основные термины
Зашифрование – процесс криптографического преобразования множества открытых сообщений в множество
Расшифрование – процесс криптографического преобразования закрытых сообщений в открытые
Дешифрование – процесс нахождения открытого сообщения, соответствующего заданному закрытому при неизвестном криптографическом преобразовании
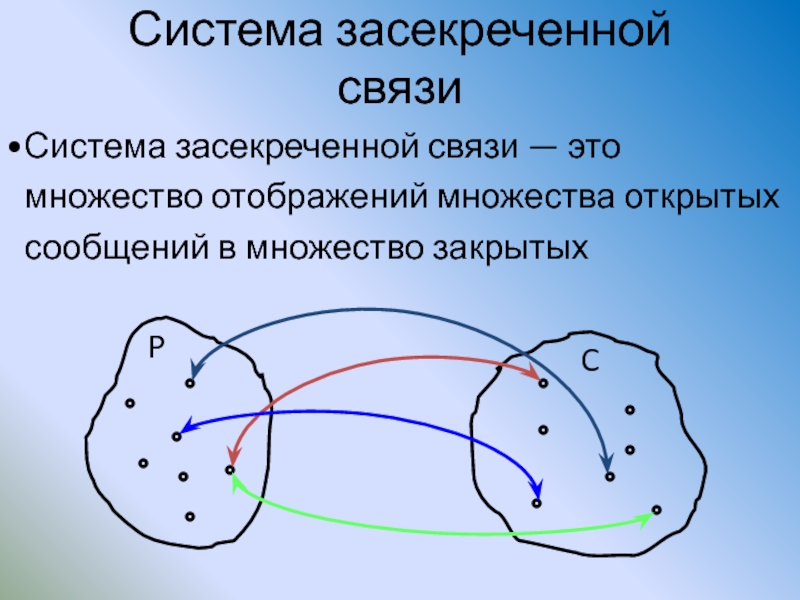
Слайд 21Система засекреченной связи
Система засекреченной связи — это множество отображений множества открытых
P
C
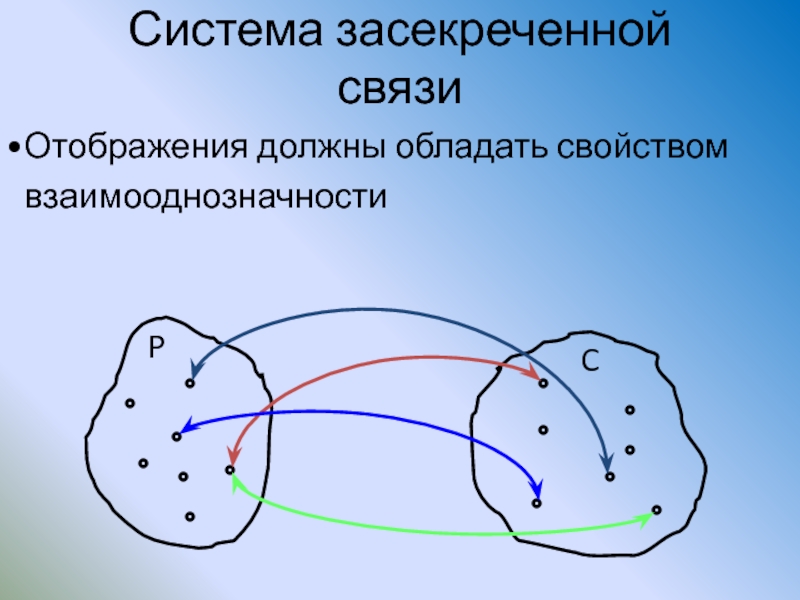
Слайд 23Система засекреченной связи
Зашифрование
Расшифрование
Открытый текст
Зашифрованное сообщение
Открытый текст
Источник ключей
Ключ 1
Ключ 2
Слайд 24Основные термины
Выбор конкретного типа преобразования определяется ключом расшифрования (или зашифрования)
Множество, из
Слайд 25Работа системы засекреченной связи
Из ключевого пространства выбираются ключи К1 и К2
Зашифрованное сообщение С пересылают по каналу передачи данных
Слайд 26Работа системы засекреченной связи
Зашифрованное сообщение С пересылают по каналу передачи данных
На
Слайд 27Формула вычисления числа необходимых ключей
N=(время жизни ключа) /
Время жизни ключа. Меньше 25 лет.
Скорость подбора ключа. Например, рассмотрим алгоритм DES. За 20 млн. долл. можно создать ЭВМ, которая раскроет шифр за сутки. Но на создание такой ЭВМ уйдет до пяти лет, а это приемлемый срок жизни стандартов и шифров.
Шанс взлома. Весьма индивидуальная величина. Обычно она равна 10-3 – 10-6 в зависимости от области применения.
Слайд 29Криптостойкость
Стойкость алгоритма шифрования (криптостойкость) — способность противостоять всем возможным атакам
против него
Слайд 30Раскрытие системы засекреченной связи (алгоритма шифрования)
полное раскрытие. Противник находит путем вычислений
нахождение эквивалентного алгоритма. Противник находит алгоритм, функционально эквивалентный алгоритму зашифрования, не имея при этом представления об используемом секретном ключе;
Слайд 31Раскрытие системы засекреченной связи (алгоритма шифрования)
нахождение открытого сообщения. Противник находит открытое
частичное раскрытие. Противник получает частичную информацию об используемом ключе или об открытом сообщении.
Слайд 32Атаки на криптоалгоритмы
Атака с известным шифртекстом (ciphertext-only attack). Противнику известен лишь
Это соответствует модели внешнего нарушителя, который имеет физический доступ к линии связи, но не имеет доступа к аппаратуре шифрования и дешифрования;
Слайд 33Атаки на криптоалгоритмы
Атака с известным открытым текстом (known plaintext attack). Предполагается,
Слайд 34Атаки на криптоалгоритмы
Атака с выбором открытого текста (chosen-plaintext attack). Противник имеет
Это соответствует модели внутреннего нарушителя, имеющего доступ к аппаратуре, но не имеющего доступа к ключам.
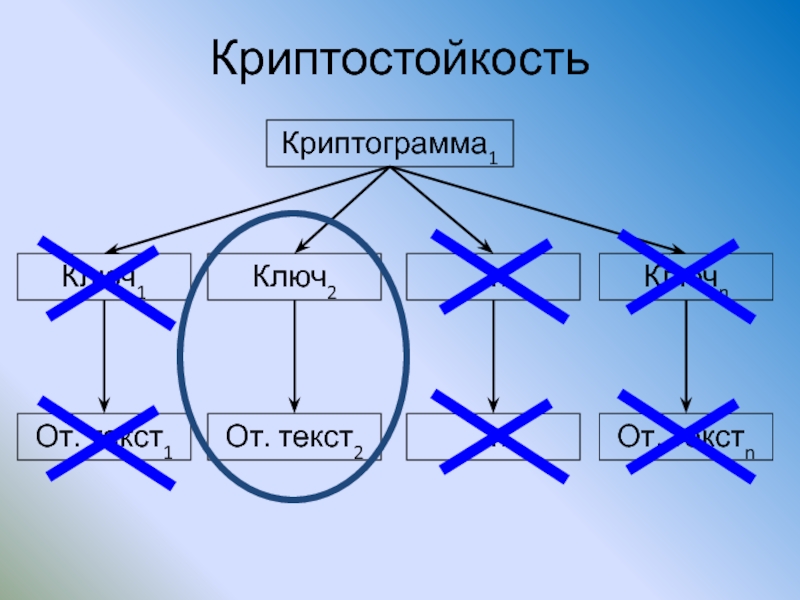
Слайд 35Криптостойкость
Стойким считается алгоритм, в котором перехват зашифрованных сообщений не приводит к
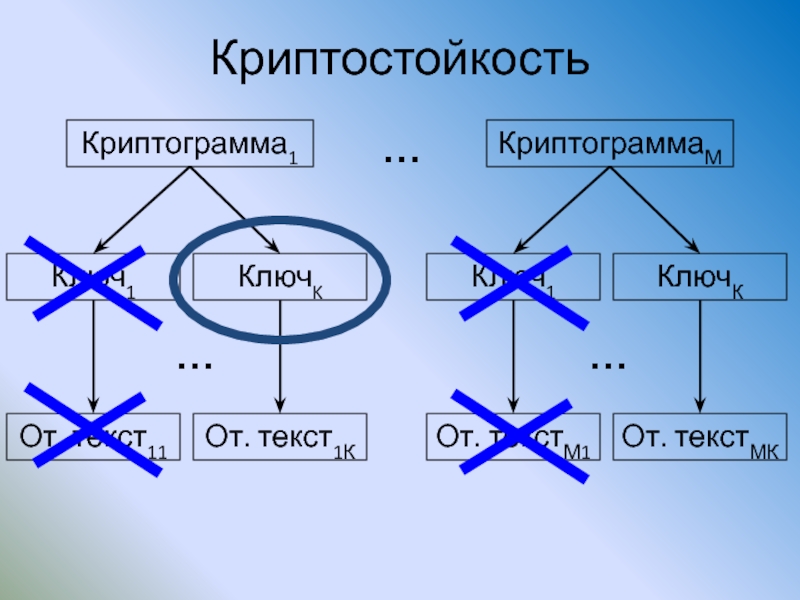
Слайд 37Криптостойкость
Криптограмма1
КлючK
От. текст1К
От. текст11
КриптограммаМ
КлючК
Ключ1
От. текстМК
От. текстМ1
…
…
…
Ключ1
Слайд 38Криптостойкость
Стойким считается алгоритм, который для своего вскрытия требует от противника:
практически недостижимых
недостижимого объема перехваченных зашифрованных сообщений или
времени раскрытия, превышающего время жизни защищенной информации
Слайд 41Типы алгоритмов шифрования
В криптографии существуют только два основных типа преобразований –
В перестановочных шифрах символы открытого текста изменяют свое местоположение.
Слайд 44Шифры замены
В шифрах замены один символ открытого текста замещается символом зашифрованного
В классической криптографии различают четыре типа шифров замены:
Шифры простой замены А → +
Шифры сложной замены А → РО4Е
Шифры блочной замены АВС → СРТ
Полиалфавитные шифры замены
Слайд 47Типы алгоритмов шифрования
В блочных шифрах открытый текст разбивается на блоки подходящей
В поточных алгоритмах каждый символ открытого текста зашифровывается независимо от других и расшифровывается таким же образом
Слайд 49Система засекреченной связи
Зашифрование
Расшифрование
Открытый текст
Зашифрованное сообщение
Открытый текст
Источник ключей
Ключ 1
Ключ 2
=
≠
Слайд 50Типы алгоритмов шифрования
Классическая схема:
ключи зашифрования и расшифрования идентичны
(симметричные криптоалгоритмы)
Схема с открытым
(асимметричные криптоалгоритмы)
Слайд 52Необходимое условие абсолютной стойкости шифра по К.Шеннону
Для того, чтобы шифр был
(т. е. алгоритм неизвестен)
Слайд 53Правило Керкхоффа
«Компрометация системы не должна причинять неудобств корреспондентам»
Стойкость (или надёжность) шифра
Оценка качества шифра должна проводиться при условии, что о данном шифре известно все, кроме использованного ключа
Слайд 54Правило Керкхоффа
Шифр – параметризованный алгоритм, состоящий из:
процедурной части (описания того, какие
параметров (различных элементов данных, используемых в преобразованиях)
Раскрытие процедурной части не должно приводить к увеличению вероятности успешного дешифрования сообщения выше допустимого предела.
Слайд 55Преимущества
разглашение конкретного шифра (алгоритма и ключа) не приводит к необходимости полной
Слайд 56Преимущества
ключи можно отчуждать от остальных компонентов системы шифрования – хранить отдельно
Слайд 57Преимущества
появляется возможность для точной оценки «степени неопределенности» алгоритма шифрования – она
Слайд 58Абсолютно стойкие шифры
Абсолютно стойкие или совершенные шифры – шифры, которые не
Слайд 59Условие абсолютной стойкости
для шифров удовлетворяющих правилу Керкхоффа:
Для того, чтобы шифр
Размер использованного для шифрования ключа должен быть не меньше размера шифруемых данных;
Ключ используется только один раз;
Все возможные значения ключа равновероятны.
Слайд 60Причины осуществления успешных атак на алгоритмы шифрования
Наличие статистической структуры исторически сложившихся
Наличие вероятных слов. (Некоторые слова и выражения более вероятны)
Слайд 61Методы, затрудняющие криптоанализ
Рассеивание (Diffusion). Влияние одного символа открытого сообщения на множество
Запутывание. Влияние одного символа ключа на множество символов зашифрованного сообщения
Перемешивание (Confusion). Рассеивание вероятных последовательностей по всему пространству возможных открытых сообщений
Слайд 72Симметричные алгоритмы
Простейшие: шифр Вернама, Цезаря, Виженера, Плэйфера
Современные:
США: DES, AES (Rijndael),
Слайд 73АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ_
Ю→А С→Ф Т→Х А→Г С→Ф _→В А→Г Л→О Е→И К→Н С→Ф У→Ц
Шифр Цезаря
сообщение: ЮСТАС АЛЕКСУ…
ключ: 3
шифртекст: АФХГФВГОИНФЦ …
Шифр Виженера.
шифртекст:АТЦПЯВБПФШФФ
Слайд 74Ю→А С→Т Т→Ц А→П С→Я _→И А→Е Л→С Е→Ш К→Ш С→Т У→Д
Шифр Виженера
сообщение: ЮСТАС АЛЕКСУ…
ключ: ВАГОНИДЕТНАСЕВЕР …
шифртекст: АТЦПЯИЕСШШТД
Наложение белого
Одноразовые системы невскрываемы!!!
Слайд 78DES
Data Encryption Standard.
Разработан в 1977 году
Длина ключа 56 бит (256 ≈7.2*1016
Размер блока 64 бита
16 раундов шифрования
Недостатки:
малая длина ключа: вскрыт за 140 дней, 450 MIPS-лет
наличие слабых ключей
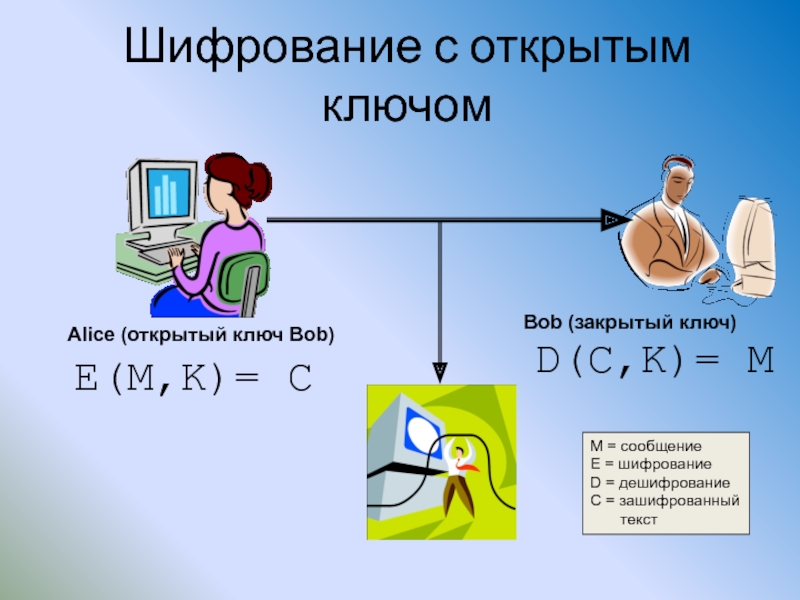
Слайд 79Шифрование с открытым ключом
Alice (открытый ключ Bob)
Bob (закрытый ключ)
E(M,K)= C
D(C,K)= M
M
E = шифрование
D = дешифрование
C = зашифрованный
текст
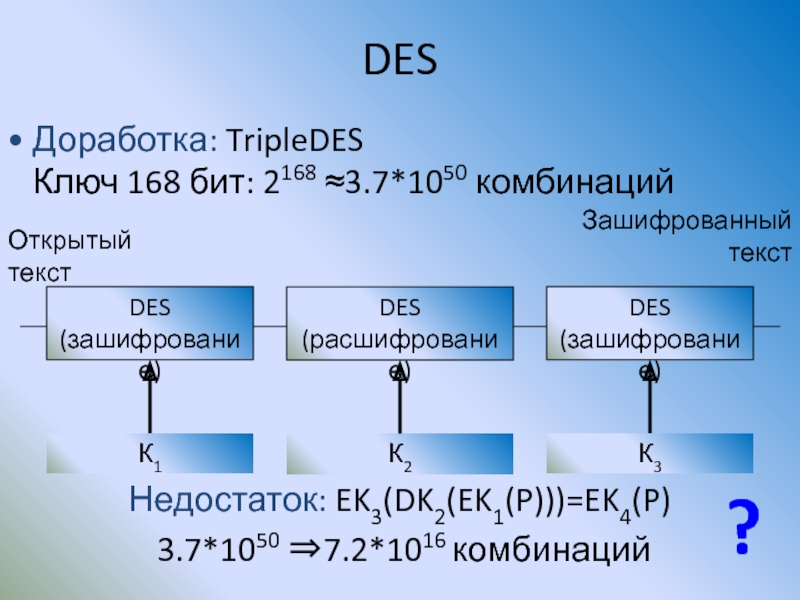
Слайд 80DES
Доработка: TripleDES
Ключ 168 бит: 2168 ≈3.7*1050 комбинаций
DES
(зашифрование)
DES
(расшифрование)
DES
(зашифрование)
Зашифрованный
текст
Открытый текст
К1
К2
К3
Недостаток: EK3(DK2(EK1(P)))=EK4(P)
3.7*1050
?
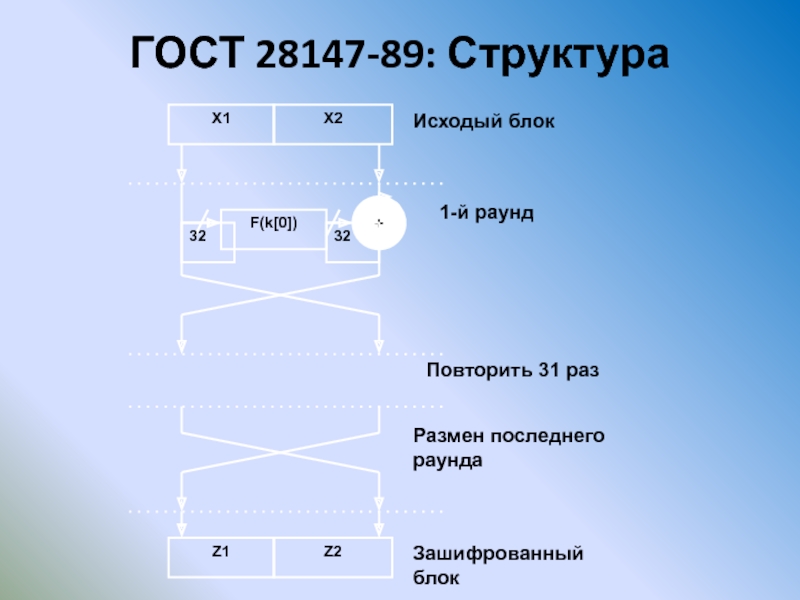
Слайд 81ГОСТ 28147-89
Системы обработки информации.
Защита криптографическая.
Алгоритм криптографического преобразования.
Принят в качестве стандарта в
Длина ключа 256 бит (2256 ≈1.2*1077 комбинаций)
32 раунда шифрования
Слайд 82ГОСТ 28147-89
4 режима работы:
простая замена
гаммирование
гаммирование с обратной связью
выработка имитовставки
Слайд 84Образующая функция ГОСТ 28147-89
32 компоненты материала ключа получаются их применением
k[0]...k[32]= К0 К1... К6 К7 К0 К1... К6 К7 К0 К1... К6 К7 К7 К6... К1 К0
Для дешифрования (по свойству симметричной сети Файштеля) используется тот же код, но с обратным порядком ключей раунда:
К0 К1... К6 К7 К7 К6... К1 К0 К7 К6... К1 К0 К7 К6... К1 К0
Слайд 86Алгоритм IDEA
IDEA: расширение ключа
k[0]...k[7]=key
key=key ROL 25
k[8]...k[15]=key
key=key ROL 25
. . .
Слайд 87Oсновные термины
Гамма шифра — псевдослучайная двоичная последовательность, вырабатываемая по заданному алгоритму,
Гаммирование — процесс наложения по определенному закону гаммы шифра на открытые данные
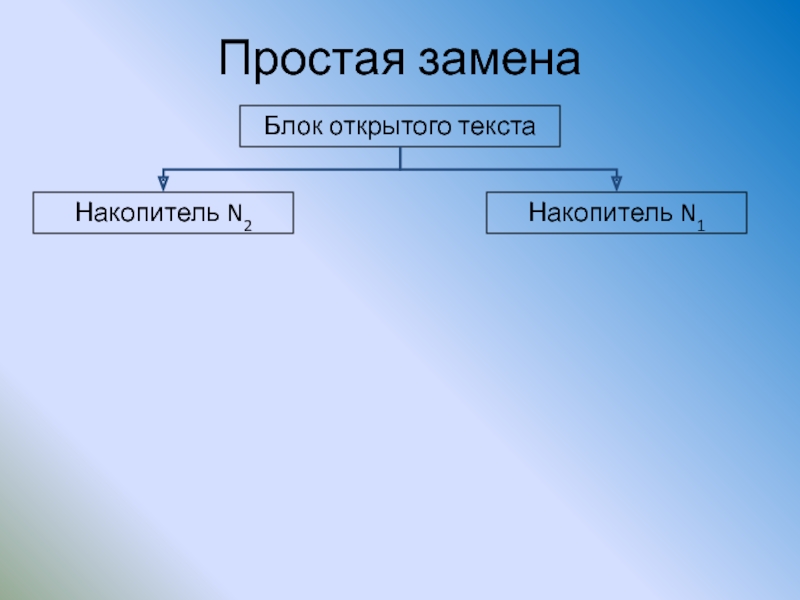
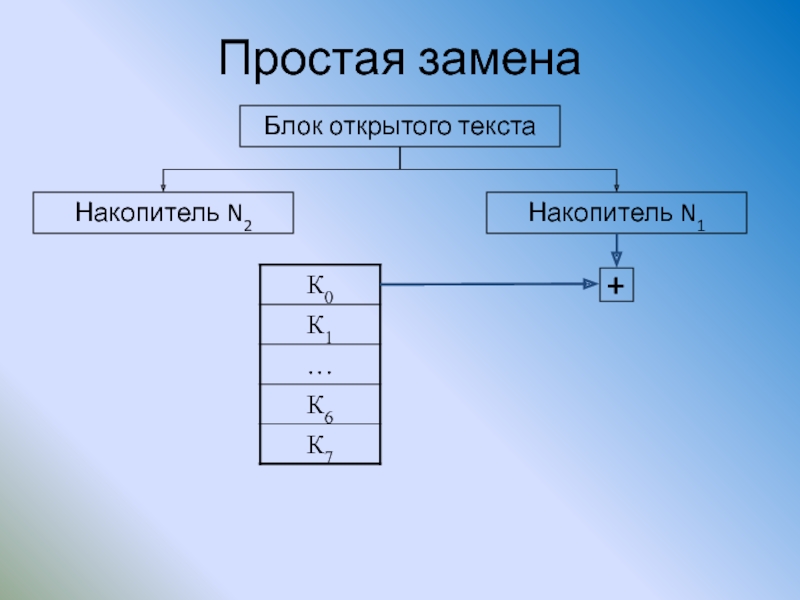
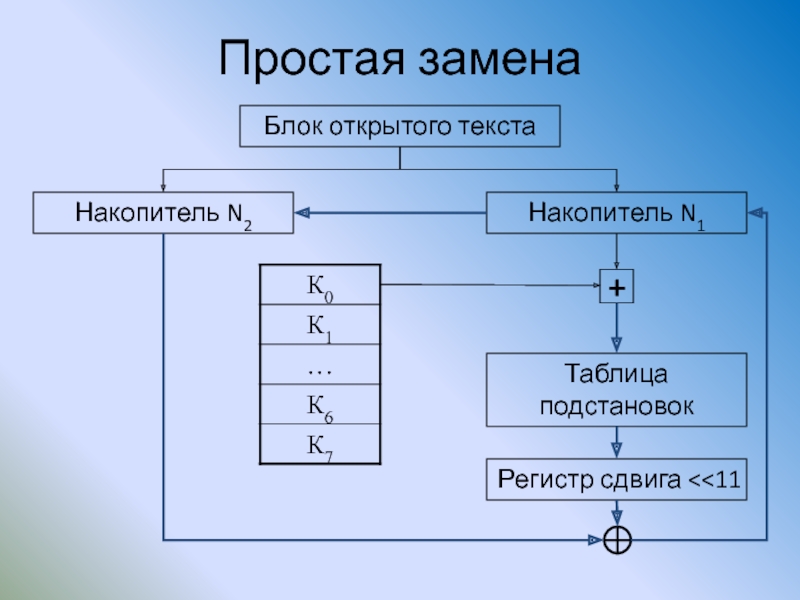
Слайд 90Простая замена
Накопитель N2
Накопитель N1
Блок открытого текста
Таблица подстановок
+
Регистр сдвига
Слайд 91Порядок использования ключей
Шифрование:
Раунды с 1-го по 24-й:
К0, K1, K2, K3, K4,
Расшифрование:
Раунды с 1-го по 24-й:
K7, K6, K5, K4, K3, K2, K1, К0
Раунды с 25-го по 32-й:
К0, K1, K2, K3, K4, K5, K6, K7
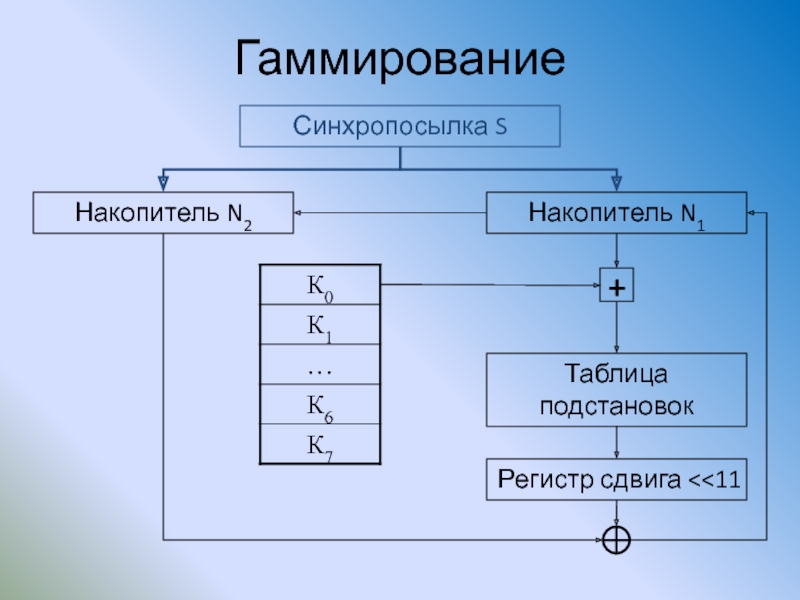
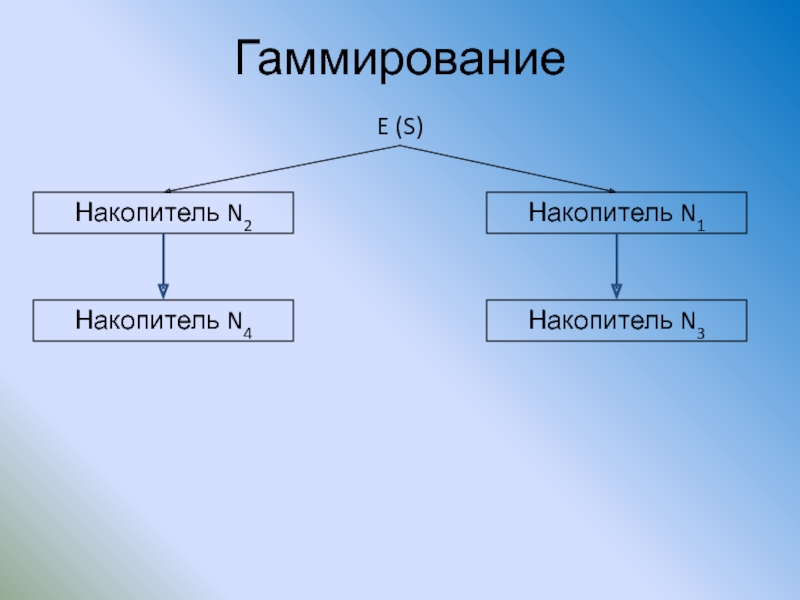
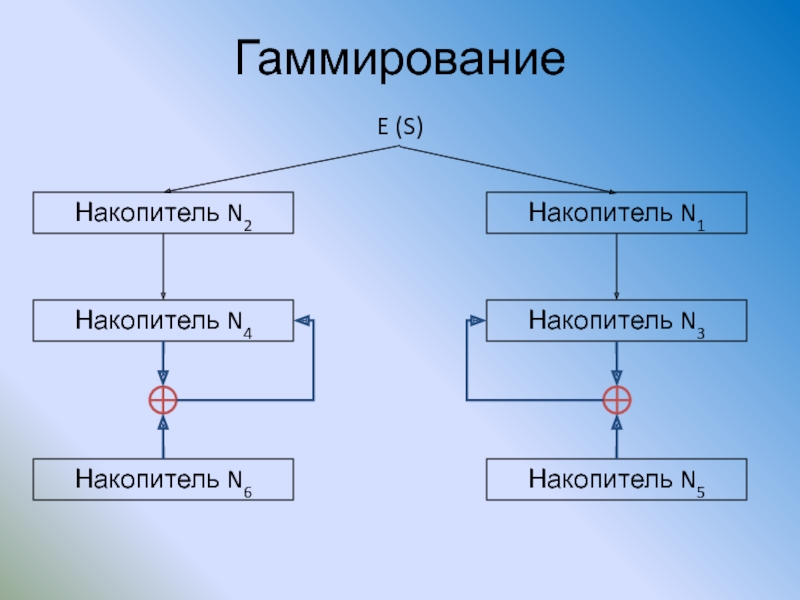
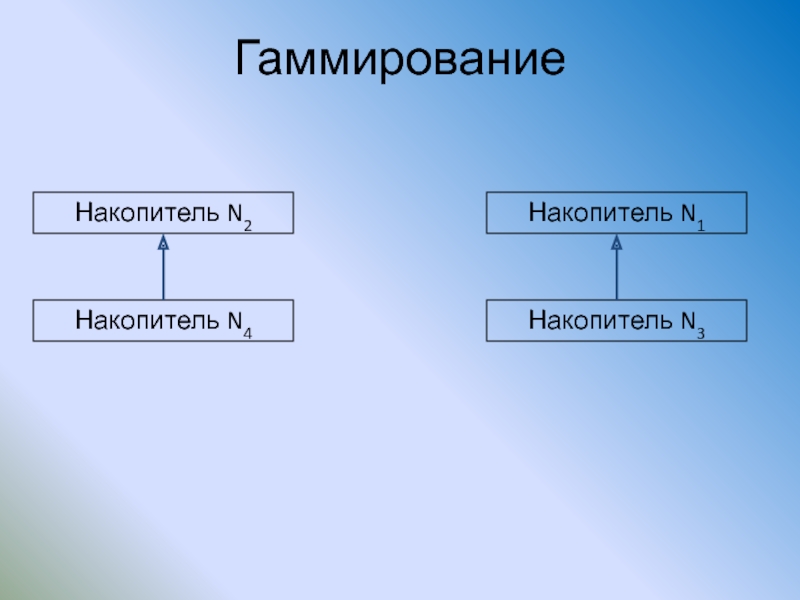
Слайд 94Гаммирование
Накопитель N2
Накопитель N1
E (S)
Накопитель N4
Накопитель N3
Накопитель N6
Накопитель N5
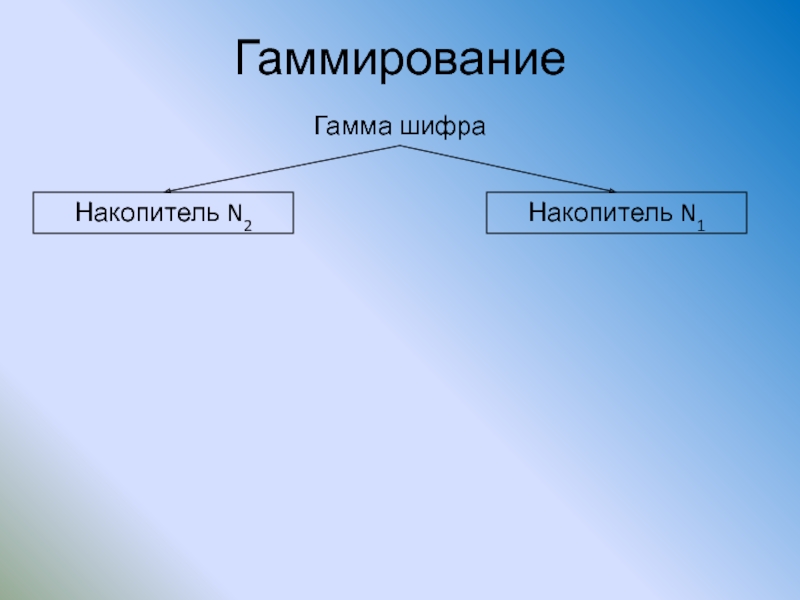
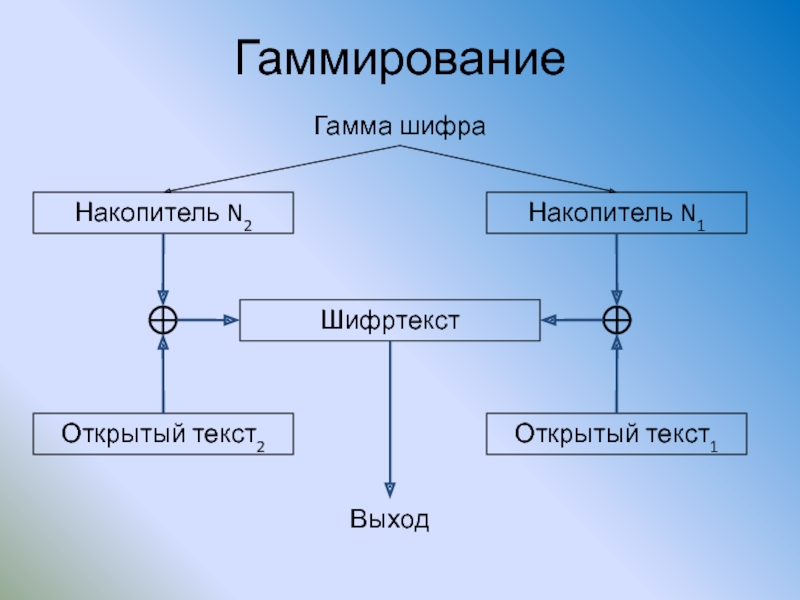
Слайд 97Гаммирование
Накопитель N2
Накопитель N1
Гамма шифра
Открытый текст2
Открытый текст1
Шифртекст
Выход
Слайд 99Основные термины
Имитозащита — защита системы шифрованной связи от навязывания ложных данных
Имитовставка
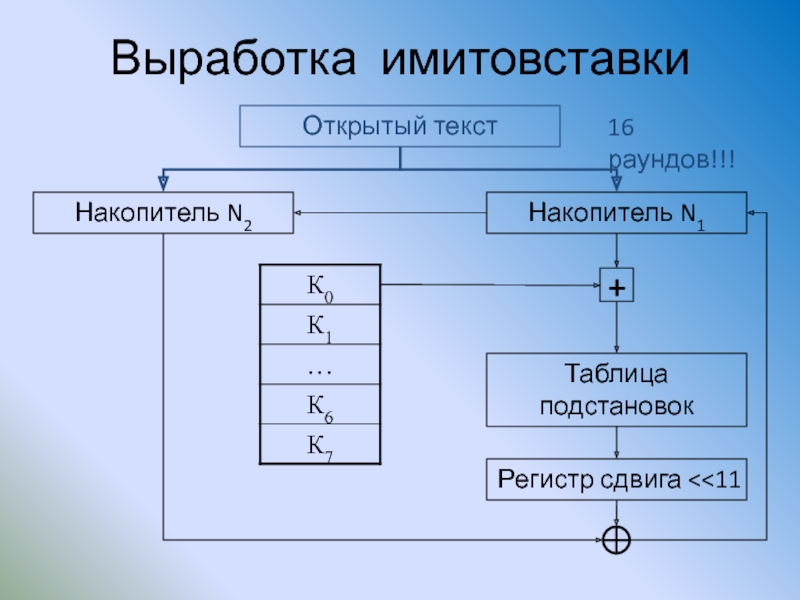
Слайд 101Выработка имитовставки
Накопитель N2
Накопитель N1
Открытый текст
Таблица подстановок
+
Регистр сдвига
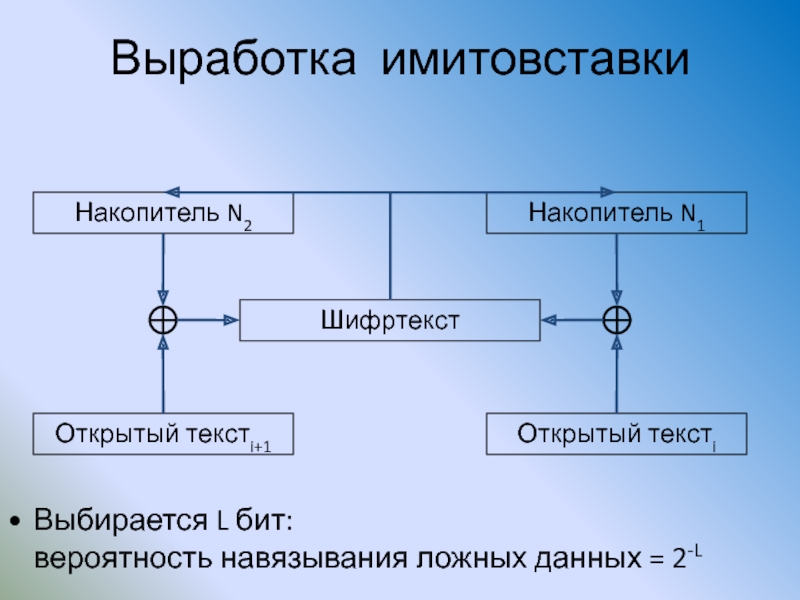
Слайд 102Выработка имитовставки
Накопитель N2
Накопитель N1
Открытый текстi+1
Открытый текстi
Шифртекст
Выбирается L бит:
вероятность навязывания ложных данных
Слайд 103ГОСТ 28147-89
Достоинства:
на сегодняшний день не предложено практически реализуемых атак, более эффективных,
большáя длина ключа (bruteforce можно пренебречь)
заполнение таблицы подстановок является секретом
Проблемы:
выбор заполнения таблицы подстановок
работа с 4-разрядными векторами
Слайд 104AES
Advanced Encryption Standard (Rijndael)
Авторы: Йон Дамен и Винсент Рэмен (Бельгия)
(J.Daemen and
размер блока 128 бит
длина ключа 128, 192, 256 бит; 10 – 14 раундов
принят 2.10.2000 NIST (www.nist.gov)
скорость работы: 7 Мбайт/с (Assembler, 200 Mhz)
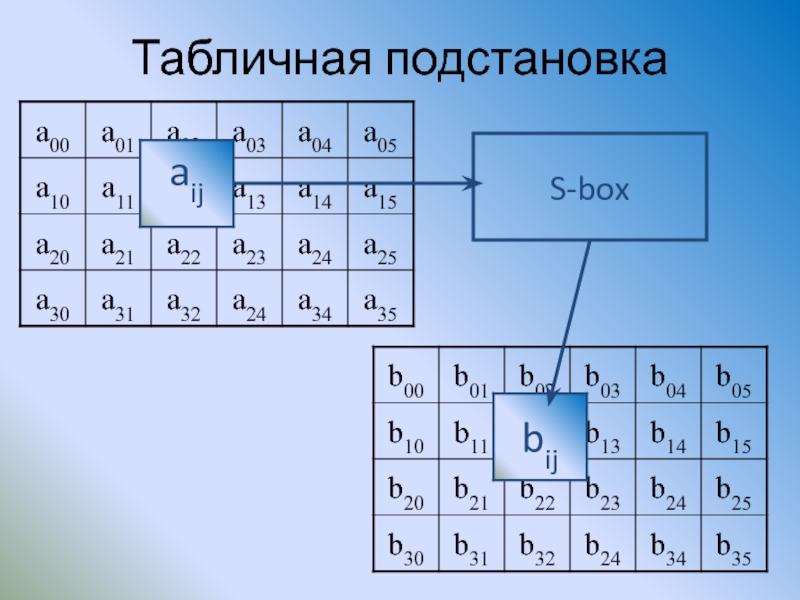
Слайд 105AES
Каждый блок кодируемых данных представляется в виде двумерного массива байт размером
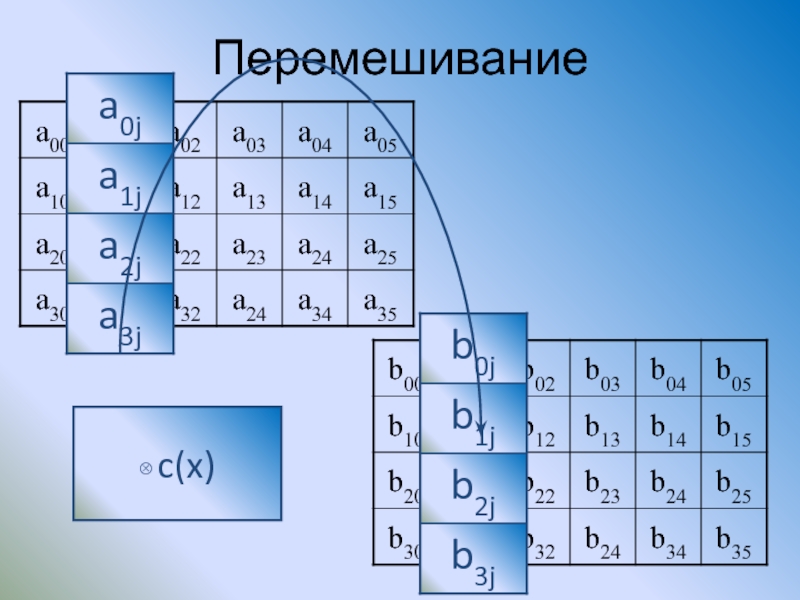
Далее преобразования производятся
либо над независимыми столбцами,
либо над независимыми строками,
либо над отдельными байтами в таблице
Слайд 110AES
Достоинства:
эффективен как на 8-битных так и на 32-битных процессорах
на многопроцессорных рабочих
Слайд 111Зашифрование и расшифрование осуществляется, например, путем сложения по модулю 2 символа открытого
Поточные алгоритмы
Главная идея: выработка на основе секретного ключа последовательности символов из входного алфавита (гаммы, ключевого потока)
Слайд 112Поточные алгоритмы. Проблемы
Стойкость зависит от обеспечения равновероятности появления очередного символа гаммы
Недопустимо
Для правильного расшифрования необходима синхронизация шифраторов
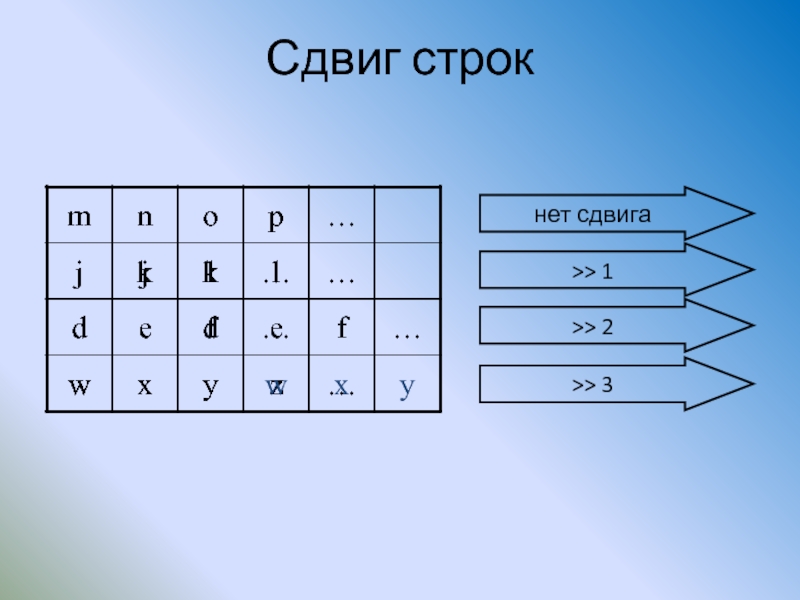
Слайд 113Методы обеспечения синхронизации
самосинхронизирующиеся шифраторы (очередной символ гаммы зависит от определенного количества
Недостаток: разрастание ошибок при расшифровании, если произошла ошибка
в ходе передачи
Достоинства: относительно стойки к пропуску символов
Слайд 114Методы обеспечения синхронизации
синхронные шифраторы (осуществляют синхронизацию только при вхождении в связь)
Недостатки:
Достоинства:полностью отсутствует размножение ошибки
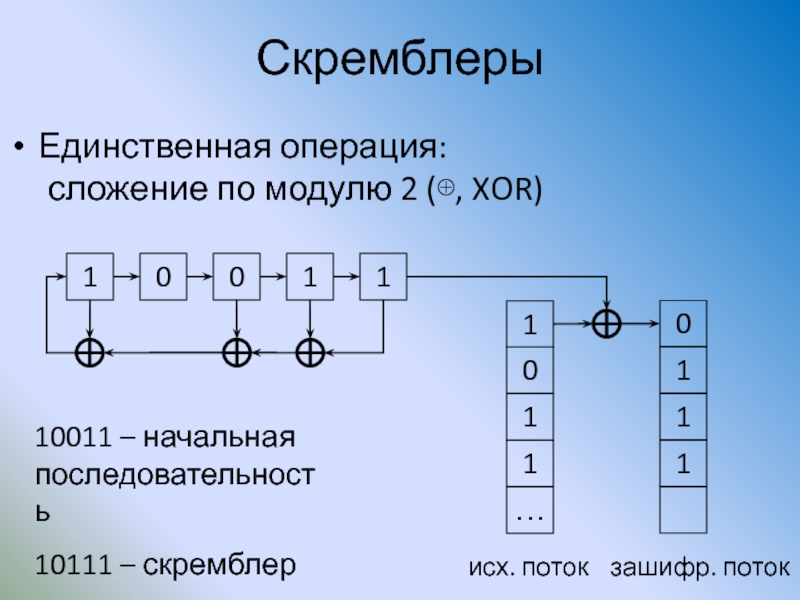
Слайд 115Скремблеры
Единственная операция:
сложение по модулю 2 (⊕, XOR)
1
1
0
1
0
1
0
1
1
…
0
1
1
1
исх. поток
зашифр. поток
10011 – начальная
10111 – скремблер
Слайд 116Скремблеры
Основная проблема: зацикливание
Зацикливание неустранимо:
N разрядов →
через 2N-1 циклов начнется повторение
Чем
Слайд 118Асимметричные алгоритмы
Уитфрид Диффи, Мартин Хеллман:
«Новые направления в криптографии», 1976 год
Идея асимметричных
с теорией односторонних функций;
с теорией сложности
Слайд 119Односторонние функции
Необратимые или односторонние функции:
y=f(x) — вычисляется легко для любого x;
найти
Под необратимостью понимают не теоретическую, а практическую невозможность вычисления обратного значения, используя современные вычислительные средства за обозримый интервал времени.
Слайд 120Проблема
На сегодняшний день теоретически не доказано существование односторонних функций
Использование односторонних функций
Слайд 121Асимметричные алгоритмы
Односторонние функции с секретом:
fz(x): Х →Y, x ∈ X
Для данного
но практически для всех z и y ∈ Y, нахождение
вычислительно неосуществимо
даже при известном Ez
Слайд 122RSA
Авторы: Rivest, Shamir, Adleman
Обнародован в 1993 г.
Принят в качестве стандарта
Стойкость базируется
Слайд 123Пример
16444757698990888364317098853 – простое?
189435747774163 • 878634363654631 =
16444757698990888364317098853
Слайд 124Генерация ключей
Выбираются два очень больших простых натуральных числа p и q,
увеличение порядка чисел ведет к замедлению работы
увеличение порядка чисел ведет к увеличению стойкости алгоритма
Правила:
Слайд 125Генерация ключей
Выбирается достаточно большое число
e, такое что 1 < e
Вычисляется большое целое d, такое что ed = 1 (mod ϕ (n)) и 1 < d < ϕ (n)
Правила:
Вычисляется модуль системы: n = p • q и
функция Эйлера: ϕ (n) = (p-1) • (q-1)
Слайд 126Секретным ключом является пара чисел (n, d),
Открытым — пара чисел
Входное сообщение разбивается на блоки mi, их размер определяется целым k, таким что
10k-1 < n < 10k
RSA
Слайд 127RSA
Секретным ключом является пара чисел (n, d),
Открытым — пара чисел
Входное сообщение разбивается на блоки mi, их размер определяется целым k, таким что
10k-1 < n < 10k
Вычисляется
Слайд 128Выбираем: p = 3; q = 11
Вычисляем: n = p •
Вычисляем: ϕ (n) = (p-1) • (q-1); ϕ (n) = 20
Выбираем: e, 1 < e < ϕ (n), взаимно простое с ϕ (n) e = 7
Выбираем: d, ed = 1 (mod ϕ (n)) и 1 < d < ϕ (n) d = 3
(7, 33) – открытый ключ; (3, 33) - закрытый
Пример
Слайд 129Сообщение:
ПОРА (04h, 03h, 05h, 02h)
47 mod 33 = 16
16384 mod
37 mod 33 = 9 2187 mod 33 = 66•33 + 9
57 mod 33 = 14 78125 mod 33 = 2367•33 + 14
27 mod 33 = 29 128 mod 33 = 3•33 + 29
Пример
Слайд 130Шифртекст: (16, 9, 14, 29)
или (10h, 09h, 0Еh, 1Dh)
163 mod 33 = 4
93 mod 33 = 3 729 mod 33 = 22•33 + 3
143 mod 33 = 5 2744 mod 33 = 83•33 + 5
293 mod 33 = 2 24389 mod 33 = 739•33 + 2
Пример
Слайд 131Проблемы RSA
Некорректный выбор p и q
Наличие нешифруемых блоков
Критичность к некоторым видам
Слайд 132Основные разновидности асимметричных алгоритмов
RSA (разложение на множители)
Эль-Гамаля (дискретное логарифмирование)
на основе эллиптических
Слайд 134Хэш-функции
Хэш-функции — функции, отображающие последовательность произвольной длины в значение фиксированной длины,
Варианты на основе:
На основе трудновычисляемой математической задачи;
На основе алгоритмов блочного шифрования;
Разработанные с нуля.
Слайд 135Хэш-функции
Основные требования:
отсутствие коллизий, т.е. невозможность найти такие значения x ≠ y,
отсутствие корреляции, т.е. отсутствие пар значений x ≠ y,
таких что H (h(x) ⊕ h(y)) < H(M)
Слайд 136Хэш-функции
SHA (Security Hash Algorithm)
Разработчики: NIST & RSA
Последовательности до 264 бит
Генерирует хэш-код
ГОСТ Р 34.11 – 94
На основе ГОСТ 28147-89
Нет ограничения на длину входной последовательности
Генерирует хэш-код длиной 256 бит
Слайд 138ЭЦП
Цель подписи:
гарантирование истинности письма путем сличения подписи с имеющимся образцом
гарантирование авторства
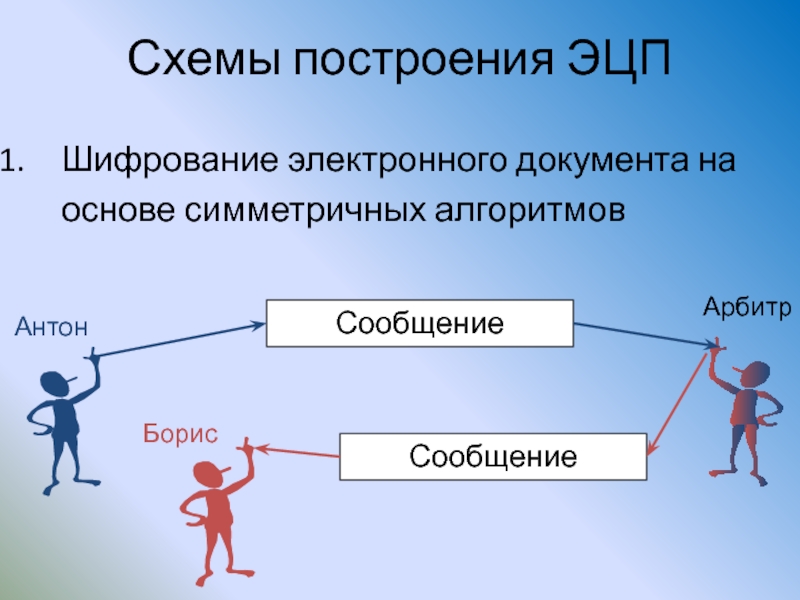
Слайд 139Схемы построения ЭЦП
Шифрование электронного документа на основе симметричных алгоритмов
Сообщение
Сообщение
Арбитр
Антон
Борис
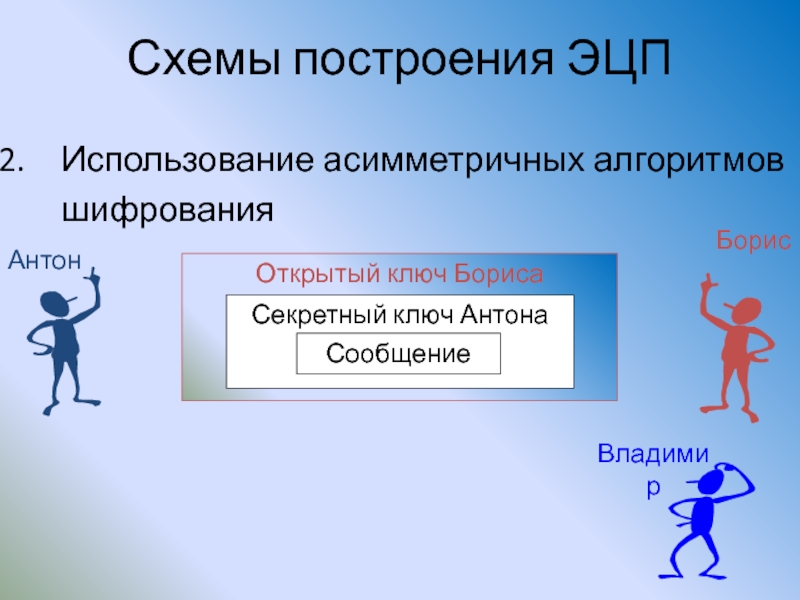
Слайд 140Схемы построения ЭЦП
Использование асимметричных алгоритмов шифрования
Сообщение
Антон
Борис
Владимир
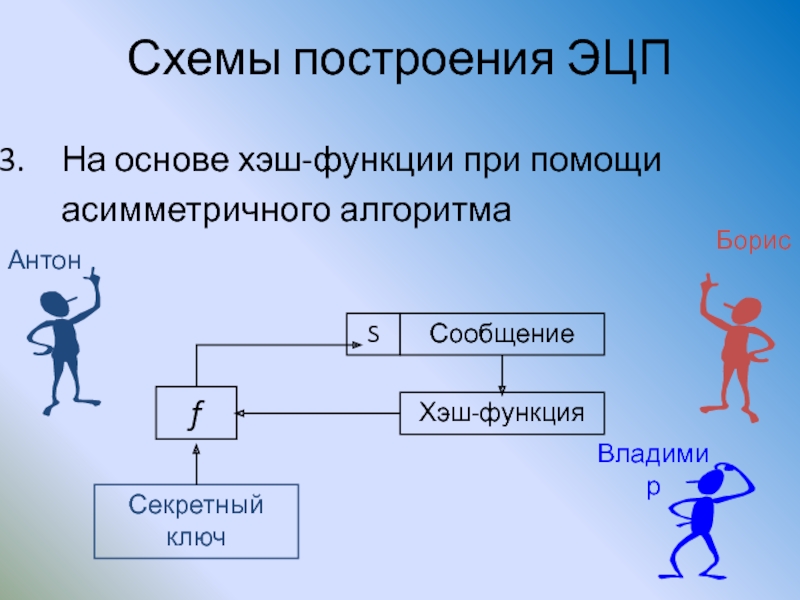
Слайд 141Схемы построения ЭЦП
На основе хэш-функции при помощи асимметричного алгоритма
Сообщение
Антон
Борис
Владимир
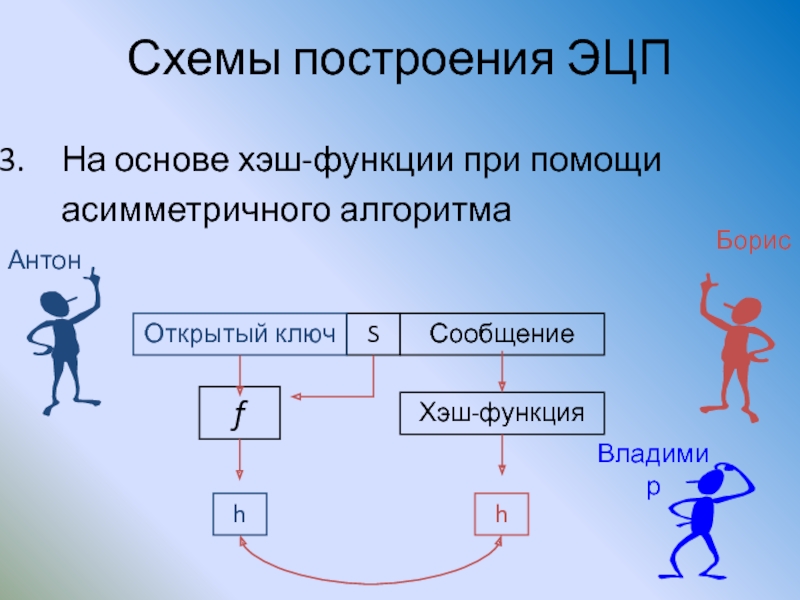
Слайд 142Схемы построения ЭЦП
На основе хэш-функции при помощи асимметричного алгоритма
Сообщение
S
Открытый ключ
Антон
Борис
Владимир
Слайд 144Отказ (ренегатство)
Сообщение
А заявляет, что он не посылал сообщения участнику Б, хотя
Антон
Борис
Слайд 145Модификация
Сообщение
Б, приняв сообщение, изменяет его и утверждает, что именно данное
Антон
Борис
Слайд 146Подделка
Сообщение
Б формирует сообщение и утверждает, что именно данное (сформированное) сообщение
Антон
Борис
Слайд 147Навязывание
Сообщение
Злоумышленник В перехватывает обмен сообщениями между А и Б и
Антон
Борис
Владимир
Слайд 148Имитация
Сообщение
Злоумышленник В пытается отправлять сообщения от имени одного из участников
Антон
Борис
Владимир
Слайд 149Основные достоинства и недостатки «классических» (симметричных)
и «новых» (асимметричных) алгоритмов
Симметричные
быстрые;
стойкие при относительно
проблема распространения ключей
Асимметричные
медленные;
требуется использовать более длинные ключи;
не требуется распространять секретные ключи
Конечно, речь идет о хороших профессиональных шифрах; сравнение - при прочих равных условиях.
Слайд 150Примерное соответствие длин ключей для симметричных и асимметричных криптосистем, обеспечивающих равную
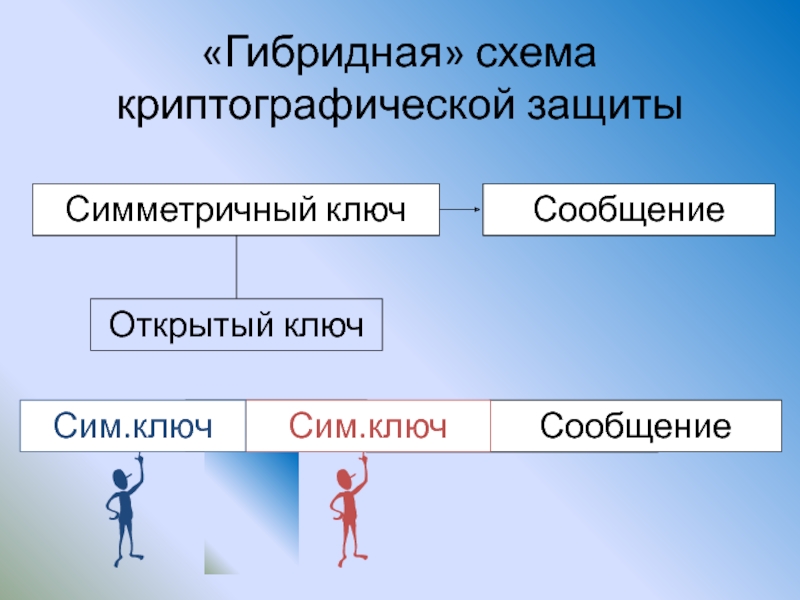
Слайд 151«Гибридная» схема
криптографической защиты
Генерация сеансового ключа
и распространение его
в зашифрованном с использованием
Использование сеансового ключа
в качестве ключа шифрования
и расшифрования всей передаваемой
в течение данного сеанса информации по «классической» схеме
Слайд 153Вероятностные шифры
Одним из перспективных способов повышения стойкости известных шифров является задание
Ti, i = 1,…, L – исходный алфавит
fi , i = 1,…, L – частоты появления букв
Ti → ψ∈Ψi, Ψi ∩ Ψj = 0, i ≠ j,
количество элементов в Ψi = fi
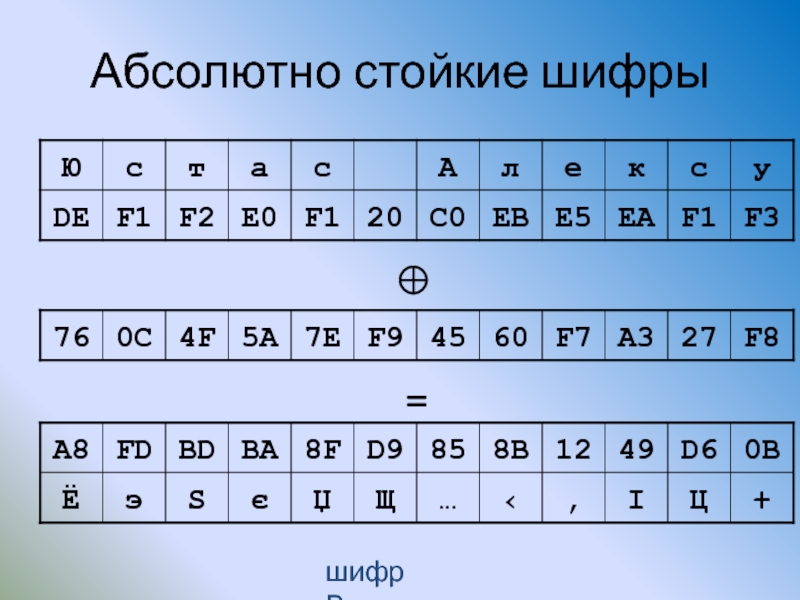
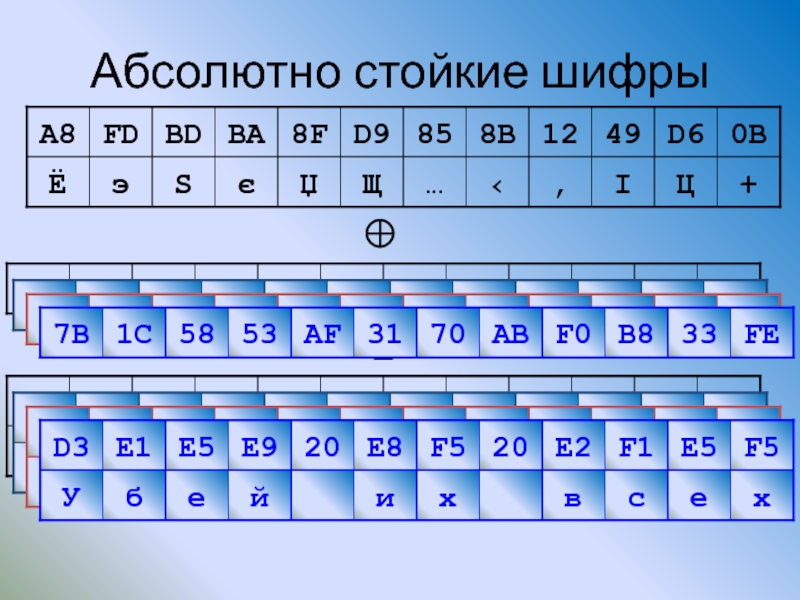
Слайд 154Вероятностные шифры
Сообщение: ЮСТАС АЛЕКСУ
А → {Б, В} Е → {Г} К →
Шифртекст: МЗКБЖНВЕДИЛ,
МЖКВИНБЕДЗЛ
Все символы сообщения равновероятны!
































































![Образующая функция ГОСТ 28147-89 32 компоненты материала ключа получаются их применением в следующем порядке:k[0]...k[32]= К0](/img/tmb/4/300268/2c59d192639915211f8fba4d3d1f2ce1-800x.jpg)
![Алгоритм IDEA IDEA: расширение ключаk[0]...k[7]=keykey=key ROL 25k[8]...k[15]=keykey=key ROL 25. . .](/img/tmb/4/300268/8723ba107013887f44903cdb85b7be1a-800x.jpg)