- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия алгебры логики. Логические выражения и логические операции презентация
Содержание
- 1. Основные понятия алгебры логики. Логические выражения и логические операции
- 2. Логика (древнегреч. – слово logos, означает «мысль,
- 3. Клод Шеннон (1916-2001). Его исследования позволили применить
- 4. Джордж Буль (1815-1864) английский математик и
- 5. В русском языке высказывания выражаются повествовательными предложениями:
- 6. Высказывание или нет? Зимой идет дождь. Снегири
- 7. Если высказывание истинно, то значение соответствующей ему
- 8. Сложное логическое высказывание строится из простых с
- 9. Инверсия - логическая операция, которая каждому высказыванию
- 10. Все операции алгебры логики определяются таблицами истинности
- 11. Вывод: если исходное выражение истинно, то результат
- 12. Дизъюнкция - логическая операция, которая каждым двум
- 13. Вывод: Логическая операция дизъюнкция ложна, если оба
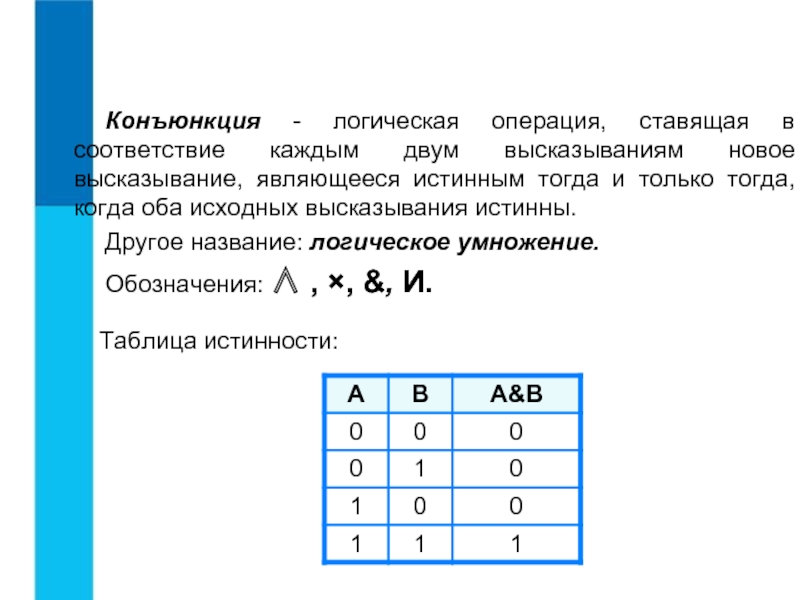
- 14. Конъюнкция - логическая операция, ставящая в соответствие
- 15. Вывод: Логическая операция конъюнкция истинна только в
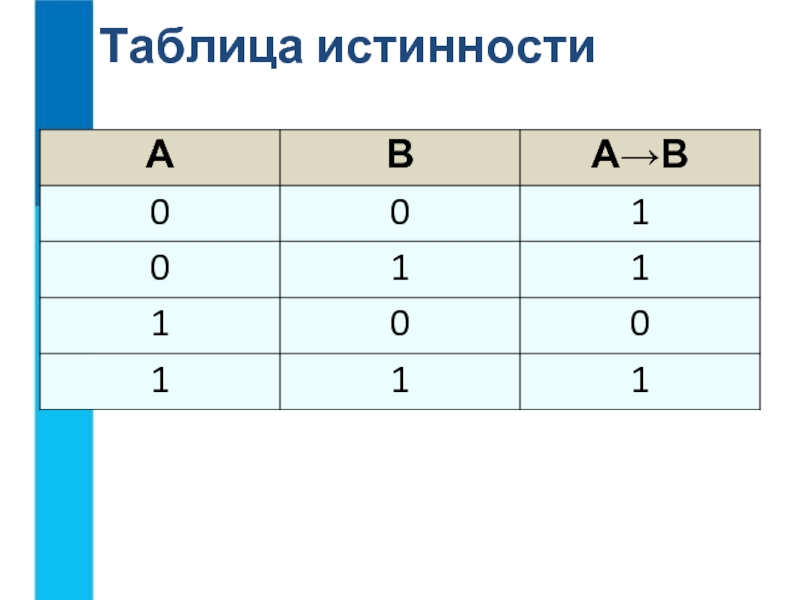
- 16. Следование (импликация) – эта операция связывает два
- 17. Вывод: Результат операции следования (импликации) ложен только
- 18. Таблица истинности
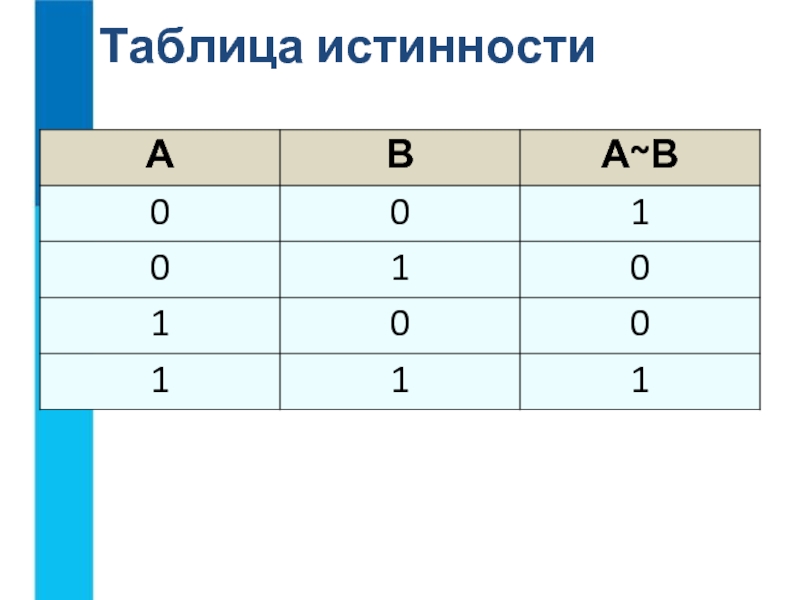
- 19. Равнозначность (эквивалентность) –логическое выражение содержит конструкцию «А
- 20. Вывод: результат операции эквивалентность истинен только тогда,
- 21. Таблица истинности
- 22. Инверсия Конъюнкция Дизъюнкция Импликация Эквивалентность Для
Слайд 2Логика (древнегреч. – слово logos, означает «мысль, понятие, рассуждение, закон») -
Алгебра логики изучает общие операции над высказываниями.
Слайд 3Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной
Логика
Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).
Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).
Слайд 4Джордж Буль
(1815-1864) английский математик и логик
Основы алгебры логики (булева алгебра)
Слайд 5В русском языке высказывания выражаются повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва -
Высказывание
Высказывание (суждение) - это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывания можно сказать истинно оно или ложно.
Слайд 6Высказывание или нет?
Зимой идет дождь.
Снегири живут в Крыму.
Кто к нам пришел?
У
Как пройти в библиотеку?
Переведите число в десятичную систему.
Запишите домашнее задание
Слайд 7Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей
0 и 1 называются логическими значениями.
Логические выражения бывают простые или сложные.
Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В нём возможно только два результата – либо «истина», либо «ложь».
Слайд 8Сложное логическое высказывание строится из простых с помощью связок «И», «ИЛИ»,
Основные логические операции:
НЕ (логическое отрицание, инверсия)
ИЛИ (логическое сложение, дизъюнкция)
И (логическое умножение, конъюнкция)
Слайд 9Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое
Другое название: логическое отрицание.
Обозначения: НЕ, ¬ , ¯ .
Логические операции
Таблица истинности:
Слайд 10 Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет
Слайд 11Вывод: если исходное выражение истинно, то результат его отрицания будет ложным,
Слайд 12Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие
Другое название: логическое сложение.
Обозначения: V, |, ИЛИ, +.
Таблица истинности:
Слайд 13Вывод: Логическая операция дизъюнкция ложна, если оба простых высказывания ложны. В
Слайд 14Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое
Другое название: логическое умножение.
Обозначения: ∧ , ×, &, И.
Таблица истинности:
Слайд 15Вывод: Логическая операция конъюнкция истинна только в том случае, если оба
Слайд 16Следование (импликация) – эта операция связывает два простых логических выражения, из
Обозначается →.
Слайд 17Вывод: Результат операции следования (импликации) ложен только тогда, когда предпосылка А
Слайд 19Равнозначность (эквивалентность) –логическое выражение содержит конструкцию «А ТОГДА И ТОЛЬКО ТОГДА,
Обозначается ~.