- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные этапы разработки и исследования моделей на компьютере презентация
Содержание
- 1. Основные этапы разработки и исследования моделей на компьютере
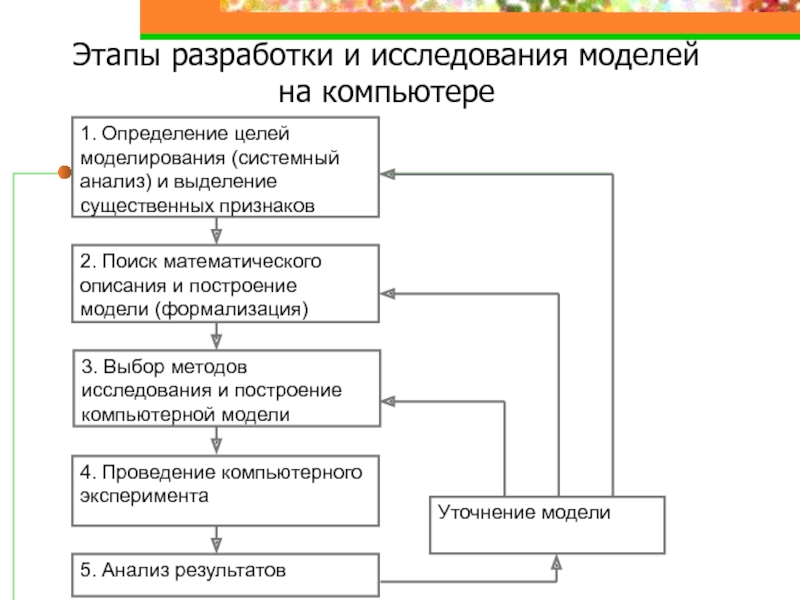
- 2. Этапы разработки и исследования моделей на компьютере
- 3. Задание 1 На научный семинар собрались ученые
- 4. Решение Постановка задачи. Пусть x – количество
- 5. Решение Математическая модель. В3=В1*(В1-1) Компьютерный эксперимент.
- 6. Решение В результате проведенного эксперимента получаем ответ:
- 7. Ответ: 15 человек.
- 8. Задание 2 Знаменатель правильной дроби на 2
- 9. Решение Постановка задачи. Пусть x – числитель
- 10. Решение Математическая модель. В математической модели уравнение
- 11. Решение Компьютерный эксперимент.
- 12. Решение Анализ полученных результатов. Проверить правильность нашей модели можно, решив линейное уравнение.
- 13. Ответ: 3/5
- 14. Задание 3 Участники шахматного турнира после окончания
- 15. Решение Указание: Данную задачу следует решать, используя
- 16. Ответ: 21 человек
Слайд 3Задание 1
На научный семинар собрались ученые и обменялись друг с другом
визитными карточками. Всего было роздано 210 визитных карточек. Сколько ученых приехало на семинар, если известно, что их было не более 20?
Слайд 4Решение
Постановка задачи. Пусть x – количество ученых, приехавших на семинар. Так
как в процессе обмена каждый раздает по одной карточке всем, кроме себя, то он раздаст (x-1) карточку. Следовательно, всего будет роздано n = x*(x-1) карточек.
Слайд 5Решение
Математическая модель. В3=В1*(В1-1)
Компьютерный эксперимент.
Начнем эксперимент, последовательно вводя в ячейку В1 числа
2, 3, 4 и т.д.
Слайд 6Решение
В результате проведенного эксперимента получаем ответ: 15 человек.
Анализ полученных результатов.
Проверим результат,
решив уравнение.
Удовлетворяющий условию задачи корень уравнения x = 15.
Удовлетворяющий условию задачи корень уравнения x = 15.
Слайд 8Задание 2
Знаменатель правильной дроби на 2 больше числителя. Если числитель увеличить
в 5 раз, а к знаменателю прибавить 5 и сократить дробь, то в результате получится 3/2. Найти исходную дробь.
Слайд 9Решение
Постановка задачи. Пусть x – числитель исходной дроби. Тогда x +
2 – знаменатель исходной дроби, 5x – новый числитель, (x + 2) + 5 = x + 7 – новый знаменатель.
Так как по условию задачи новая дробь после сокращения равна 3/2, составляем уравнение: 5x/(x + 7)=3/2.
Так как по условию задачи новая дробь после сокращения равна 3/2, составляем уравнение: 5x/(x + 7)=3/2.
Слайд 10Решение
Математическая модель. В математической модели уравнение представляет собой пропорцию. Воспользуемся основным
свойством пропорции – произведение крайних членов равно произведению средних членов, т.е. 5x * 2=(x +7) * 3.
Слайд 11Решение
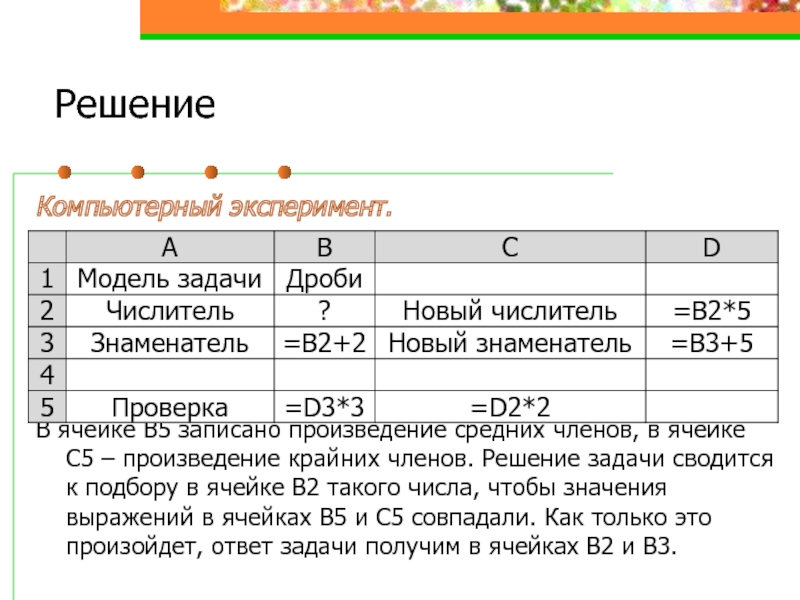
Компьютерный эксперимент.
В ячейке В5 записано произведение средних членов, в ячейке С5
– произведение крайних членов. Решение задачи сводится к подбору в ячейке В2 такого числа, чтобы значения выражений в ячейках В5 и С5 совпадали. Как только это произойдет, ответ задачи получим в ячейках В2 и В3.
Слайд 12Решение
Анализ полученных результатов.
Проверить правильность нашей модели можно, решив линейное уравнение.
Слайд 14Задание 3
Участники шахматного турнира после окончания очередной партии обменялись друг с
другом рукопожатиями. Всего сыграно 210 партий, значит, 210 раз противники пожали друг другу руки. Сколько человек принимали участие в турнире, если каждый сыграл по одному разу со всеми остальными и известно, что участников было не более 30?
Слайд 15Решение
Указание: Данную задачу следует решать, используя таблицу задания 1, исправив содержимое
ячейки В3.
Математическая модель. Пусть n – количество рукопожатий, x – количество участников. Тогда…
Математическая модель. Пусть n – количество рукопожатий, x – количество участников. Тогда…