- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы сортировки данных презентация
Содержание
- 1. Методы сортировки данных
- 2. Сортировка объектов – расположение объектов по возрастанию или убыванию согласно определенному линейному отношению порядка
- 3. Сортировка объектов: Внутренняя Внешняя
- 4. Внутренняя сортировка оперирует с массивами, целиком помещающимися
- 6. Алгоритм сортировки вставкой
- 7. Суть сортировки: Упорядочиваются два элемента
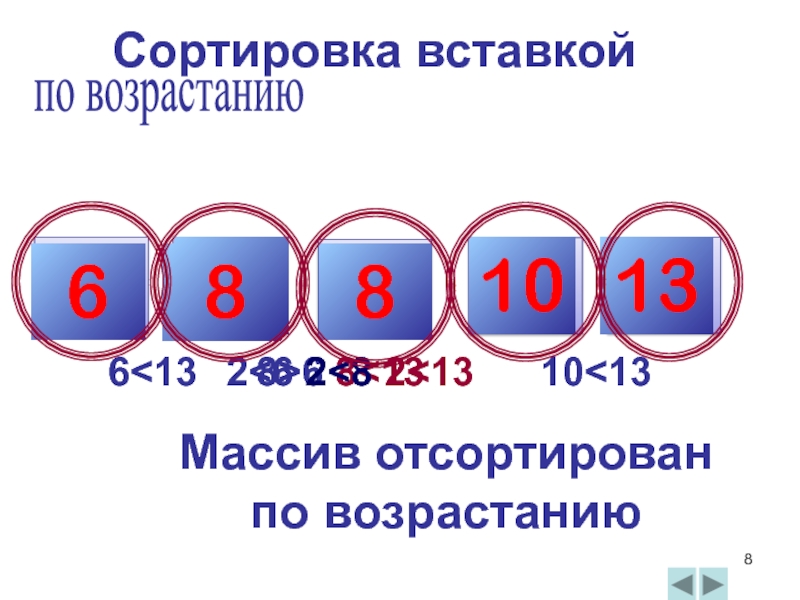
- 8. Сортировка вставкой 13 6 2 10 8
- 9. Пусть нужно отсортировать массив А по возрастанию,
- 10. Начало алгоритма. Шаг 1 j:=2, Шаг 2
- 11. Начало алгоритма. Шаг 1 j:=2, Шаг 2
- 12. Начало алгоритма. Шаг 1 j:=2, Шаг 2
- 13. Начало алгоритма. Шаг 1 j:=2, Шаг 2
- 14. Начало алгоритма. Шаг 1 j:=2, Шаг 2
- 15. Начало алгоритма. Шаг 1 j:=2, Шаг 2
- 16. Начало алгоритма. Шаг 1 j:=2, Шаг 2
- 17. Алгоритм сортировки выбором
- 18. Суть сортировки: Выбирается элемент с наименьшим значением
- 19. 13 6 2 10 8 Сортировка выбором
- 20. Постановка задачи Пусть нужно отсортировать массив А
- 21. Начало алгоритма. Шаг 1 j:=1, Шаг 2 Пока j
- 22. Начало алгоритма. Шаг 1 j:=1, Шаг 2 Пока j
- 23. Начало алгоритма. Шаг 1 j:=1, Шаг 2 Пока j
- 24. Алгоритм сортировки обменом («пузырьковая»)
- 25. Суть сортировки: Последовательно просматривается массив и
- 26. Сортировка обменом 13 6 2 10 8
- 27. Пусть нужно отсортировать массив А по возрастанию,
- 28. Начало алгоритма. Шаг 1 j:=N, Шаг 2
- 29. Начало алгоритма. Шаг 1 j:=N, Шаг 2
- 30. Начало алгоритма. Шаг 1 j:=N, Шаг 2
- 31. Алгоритм сортировки Шелла
- 32. Классифицируется как «слияние вставкой»; Называется «сортировкой
- 33. Условия реализации: Конкретная последовательность шагов может
- 34. Суть сортировки: Сначала сортируются все элементы, отстоящие
- 35. 12 Сортировка Шелла 8 14 6 4
- 36. Сортировка Шелла 4 1 6 3 шаг.
- 37. Пусть нужно отсортировать массив А по возрастанию,
- 38. Начало алгоритма. Шаг 1. M=целая часть N/2
- 39. Начало алгоритма. Шаг 1. M=целая часть N/2
- 40. Зачем необходимо это действие? Начало алгоритма. Шаг
- 41. Зачем необходимо это действие? Начало алгоритма. Шаг
- 42. Почему условие выхода из цикла такое? Начало
- 43. Алгоритм быстрой сортировки
- 44. Придумана Ч.А.Р. Хоаром (Charles Antony Richard Hoare);
- 45. Суть сортировки: Выбирается некоторое значение (x)-
- 46. Суть сортировки: Меняем найденные элементы местами.
- 47. Быстрая сортировка 8 12 3 7 19
- 48. Пусть нужно отсортировать массив А по возрастанию,
- 49. Начало алгоритма. Шаг 1 i=m j=t Шаг 2 x=A[округление до целого(m+t)/2] Шаг 3 Пока i
- 50. Начало алгоритма. Шаг 1 i=m j=t Шаг 2 x=A[округление до целого(m+t)/2] Шаг 3 Пока i
- 51. Начало алгоритма. Шаг 1 i=m j=t Шаг 2 x=A[округление до целого(m+t)/2] Шаг 3 Пока i
- 52. Начало алгоритма. Шаг 1 i=m j=t Шаг 2 x=A[округление до целого(m+t)/2] Шаг 3 Пока i
- 53. Начало алгоритма. Шаг 1 i=m j=t Шаг 2 x=A[округление до целого(m+t)/2] Шаг 3 Пока i
- 54. Начало алгоритма. Шаг 1 i=m j=t Шаг 2 x=A[округление до целого(m+t)/2] Шаг 3 Пока i
- 55. Начало алгоритма. Шаг 1 i=m j=t Шаг 2 x=A[округление до целого(m+t)/2] Шаг 3 Пока i
- 56. Основывается: количестве необходимых сравнений количестве пересылок Оценка эффективности
- 57. Параметры оценки алгоритмов Время сортировки -
- 58. Устойчивость – отсортированный массив не меняет порядок
- 59. Естественность поведения - эффективность метода при
- 60. Оценка алгоритма сортировки выбором Общее количество
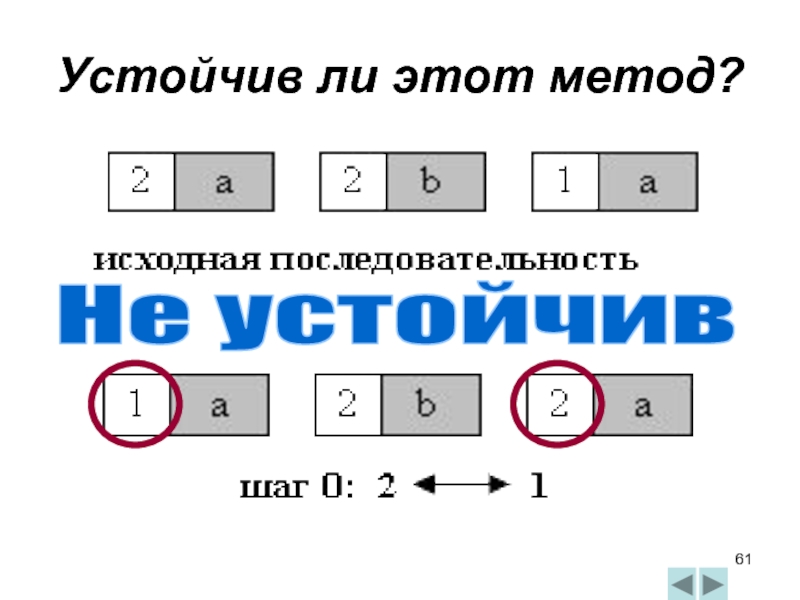
- 61. Устойчив ли этот метод? Не устойчив
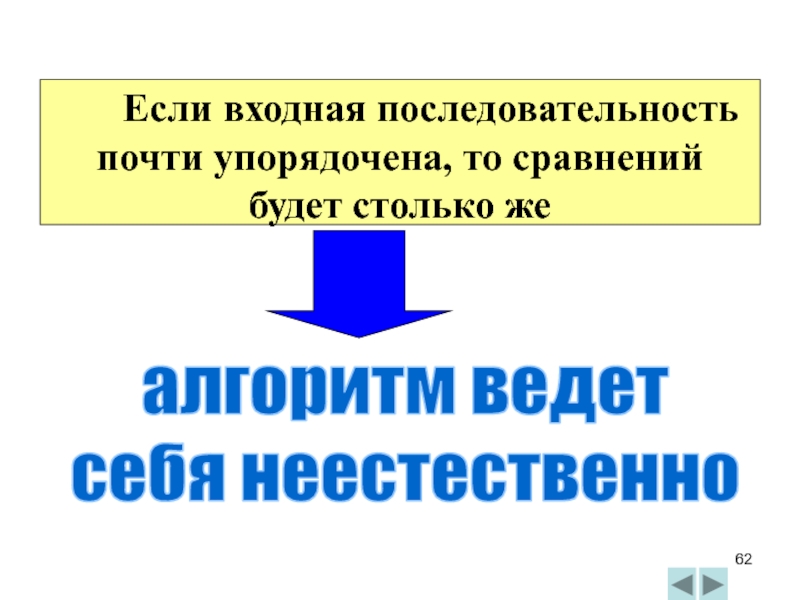
- 62. Если входная последовательность почти упорядочена, то сравнений
- 63. Оценка алгоритма сортировки вставкой Для массива
- 64. Устойчив ли этот метод? Устойчив порядок элементов с одинаковыми ключами не изменяется
- 65. Наименьшие оценки эффективности, когда элементы предварительно упорядочены,
- 66. Не эффективный метод, так как включение элемента
- 67. Оценка алгоритма сортировки обменом Количество сравнений (n2-n)/2 Общее количество операций Theta(n2)
- 68. Ответьте на следующие вопросы: Устойчив ли этот метод? Естественное ли поведение этого алгоритма?
- 69. Очень медленен и малоэффективен. На практике,
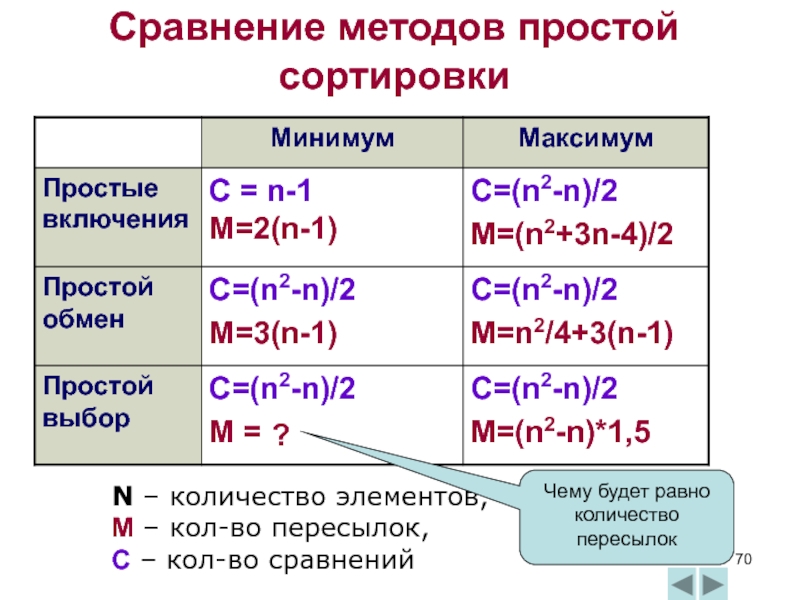
- 70. Сравнение методов простой сортировки N – количество
- 71. Выбор метода сортировки При сортировке маленьких массивов
- 72. Оценка алгоритма Шелла Время выполнения пропорционально
- 73. Оценка алгоритма быстрой сортировки Если размер
- 74. Общее количество операций Theta(n). Количество
- 75. Метод неустойчив. Поведение довольно естественно,
- 76. Итоги: Предпочтительным является метод прямого включения;
- 77. Контрольные вопросы Что такое «сортировка»? В чем
- 78. Контрольные вопросы Какой алгоритм сортировки считается самым
Слайд 1Методы сортировки
данных
Молчан Олег Николаевич, преподаватель спец. дисциплин
дисциплина «Основы алгоритмизации
Слайд 2Сортировка объектов – расположение объектов по возрастанию или убыванию согласно определенному
Слайд 4Внутренняя сортировка оперирует с массивами, целиком помещающимися в оперативной памяти с
Данные обычно сортируются на том же месте, без дополнительных затрат
Слайд 7Суть сортировки:
Упорядочиваются два элемента массива
Вставка третьего элемента в соответствующее место
Этот процесс повторяется до тех пор, пока все элементы не будут упорядочены.
Слайд 9Пусть нужно отсортировать массив А по возрастанию, в котором N элементов
Вспомогательные переменные
j – номер первого элемента остатка.
i – номер перемещаемого элемента.
f – условие выхода из цикла (если f=1, то выход)
Val – промежуточное значение, используемое для перемещения элементов массив
Постановка задачи
Слайд 10Начало алгоритма.
Шаг 1 j:=2,
Шаг 2 Пока j
Шаг 2.2.1 Если A[i-1]>A[i]
то Val:=A[i-1];
A[i-1]:=A[i];
A[i]:=Val,
иначе f:=1,
Шаг 2.2.2 i:=i-1,
Шаг 2.3 j:=j+1.
Конец алгоритма.
Слайд 11Начало алгоритма.
Шаг 1 j:=2,
Шаг 2 Пока j
Шаг 2.2.1 Если A[i-1]>A[i]
то Val:=A[i-1];
A[i-1]:=A[i];
A[i]:=Val,
иначе f:=1,
Шаг 2.2.2 i:=i-1,
Шаг 2.3 j:=j+1.
Конец алгоритма.
Что обозначает данное условие?
Слайд 12Начало алгоритма.
Шаг 1 j:=2,
Шаг 2 Пока j
Шаг 2.2.1 Если A[i-1]>A[i]
то Val:=A[i-1];
A[i-1]:=A[i];
A[i]:=Val,
иначе f:=1,
Шаг 2.2.2 i:=i-1,
Шаг 2.3 j:=j+1.
Конец алгоритма.
Почему стартовое значение j =2 ?
Слайд 13Начало алгоритма.
Шаг 1 j:=2,
Шаг 2 Пока j
Шаг 2.2.1 Если A[i-1]>A[i]
то Val:=A[i-1];
A[i-1]:=A[i];
A[i]:=Val,
иначе f:=1,
Шаг 2.2.2 i:=i-1,
Шаг 2.3 j:=j+1.
Конец алгоритма.
Почему стартовое значение i =2 ?
Слайд 14Начало алгоритма.
Шаг 1 j:=2,
Шаг 2 Пока j
Шаг 2.2.1 Если A[i-1]>A[i]
то Val:=A[i-1];
A[i-1]:=A[i];
A[i]:=Val,
иначе f:=1,
Шаг 2.2.2 i:=i-1,
Шаг 2.3 j:=j+1.
Конец алгоритма.
Всегда ли происходит обмен входного j элемента
с отсортированным элементом ?
Слайд 15Начало алгоритма.
Шаг 1 j:=2,
Шаг 2 Пока j
Шаг 2.2.1 Если A[i-1]>A[i]
то Val:=A[i-1];
A[i-1]:=A[i];
A[i]:=Val,
иначе f:=1,
Шаг 2.2.2 i:=i-1,
Шаг 2.3 j:=j+1.
Конец алгоритма.
Возможно ли заменить цикл ПОКА и ЕСЛИ
одним циклом ПОКА с условием i>=2 и A[i-1]>A[i] ?
Слайд 16Начало алгоритма.
Шаг 1 j:=2,
Шаг 2 Пока j
Шаг 2.2.1 Если A[i-1]>A[i]
то Val:=A[i-1];
A[i-1]:=A[i];
A[i]:=Val,
иначе f:=1,
Шаг 2.2.2 i:=i-1,
Шаг 2.3 j:=j+1.
Конец алгоритма.
Для чего нужен этот оператор?
Слайд 18Суть сортировки:
Выбирается элемент с наименьшим значением и делается его обмен с
Затем находится элемент с наименьшим значением из оставшихся n-1 элементов и делается его обмен со вторым элементом и т.д. до обмена двух последних элементов.
Слайд 1913
6
2
10
8
Сортировка выбором
Min
2
Min
6
Min
8
13
Min
10
13
Отсортиро-ванная часть
Отсортированная часть
Отсортированная часть
Массив отсортирован по возрастанию
по возрастанию
Слайд 20Постановка задачи
Пусть нужно отсортировать массив А по возрастанию, в котором N
Вспомогательные переменные
j – номер первого элемента остатка.
i – номер перемещаемого элемента.
min – минимальное число в массиве.
Imin – номер минимального числа в массиве
Слайд 21Начало алгоритма.
Шаг 1 j:=1,
Шаг 2 Пока j
Шаг 2.2 Пока i<=N выполнять:
Шаг 2.2.1 Если A[i]
Шаг 2.2.2 i:=i+1,
Шаг 2.3 A[Imin]:=A[j], A[j]:=min
Шаг 2.4 j:=j+1.
Конец алгоритма.
Слайд 22Начало алгоритма.
Шаг 1 j:=1,
Шаг 2 Пока j
Шаг 2.2 Пока i<=N выполнять:
Шаг 2.2.1 Если A[i]
Шаг 2.2.2 i:=i+1,
Шаг 2.3 A[Imin]:=A[j], A[j]:=min
Шаг 2.4 j:=j+1.
Конец алгоритма.
Что происходит в выделенном фрагменте?
Слайд 23Начало алгоритма.
Шаг 1 j:=1,
Шаг 2 Пока j
Шаг 2.2 Пока i<=N выполнять:
Шаг 2.2.1 Если A[i]
Шаг 2.2.2 i:=i+1,
Шаг 2.3 A[Imin]:=A[j], A[j]:=min
Шаг 2.4 j:=j+1.
Конец алгоритма.
Что происходит в выделенном фрагменте?
Слайд 25
Суть сортировки:
Последовательно просматривается массив и сравнивается каждая пара элементов между собой.
При этом "неправильное" расположение элементов устраняется путем их перестановки.
Процесс просмотра и сравнения элементов повторяется до просмотра всего массива.
Слайд 26Сортировка обменом
13
6
2
10
8
Первый просмотр
6
13
8
13
13
2
10
13
Второй просмотр
6
8
2
8
Третий просмотр
6
2
6
Четвертый просмотр
2
6
6<8
8>2
8<10
6>2
6<8
6>2
по возрастанию
Слайд 27Пусть нужно отсортировать массив А по возрастанию, в котором N элементов
Вспомогательные переменные
j – номер первого элемента остатка.
i – номер перемещаемого элемента.
Val – промежуточное значение, используемое для перемещения элементов массива
Постановка задачи
Слайд 28Начало алгоритма.
Шаг 1 j:=N,
Шаг 2 Пока j>=2 выполнять:
Шаг 2.1 i:=1; ,
Шаг
Шаг 2.2.1 Если A[i]>A[i+1]
то Val:=A[i];
A[i]:=A[i+1];
A[i+1]:=Val,
Шаг 2.2.2 i=i+1,
Шаг 2.3 j:=j-1.
Конец алгоритма.
Сравнение соседних элементов
Обмен соседних элементов местами, в случае если левый больше правого
Формируется отсортированная часть
Слайд 29Начало алгоритма.
Шаг 1 j:=N,
Шаг 2 Пока j>=2 выполнять:
Шаг 2.1 i:=1; ,
Шаг
Шаг 2.2.1 Если A[i]>A[i+1]
то Val:=A[i];
A[i]:=A[i+1];
A[i+1]:=Val,
Шаг 2.2.2 i=i+1,
Шаг 2.3 j:=j-1.
Конец алгоритма.
Почему условие такое?
Слайд 30Начало алгоритма.
Шаг 1 j:=N,
Шаг 2 Пока j>=2 выполнять:
Шаг 2.1 i:=1; ,
Шаг
Шаг 2.2.1 Если A[i]>A[i+1]
то Val:=A[i];
A[i]:=A[i+1];
A[i+1]:=Val,
Шаг 2.2.2 i=i+1,
Шаг 2.3 j:=j-1.
Конец алгоритма.
Почему значение j уменьшается?
Можно ли увеличивать? Что нужно изменить?
Слайд 32Классифицируется как «слияние вставкой»;
Называется «сортировкой с убывающим шагом»
Общий метод, который использует
Слайд 33Условия реализации:
Конкретная последовательность шагов может быть другой, но последний шаг должен
Следует избегать последовательность, которые являются степенями 2 (т.е. нельзя использовать последовательность шагов – 4,2)
?
?
Слайд 34Суть сортировки:
Сначала сортируются все элементы, отстоящие друг от друга на три
Затем сортируются элементы, расположенные на расстоянии двух позиций
Наконец, сортируются все соседние элементы
Слайд 3512
Сортировка Шелла
8
14
6
4
1
2
3
4
1
2
1 шаг. 4 группы из 2-х элементов
1
7
3
4
12
4
8
9
9
1
14
7
6
2 шаг. 2 группы
1
2
1
2
1
2
1
2
4
1
6
8
4<12
8<9
1<14
6<7
4>1
8>6
по возрастанию
4<12
12
1<4
8<9
9
6<8
12<14
14
9>7
9
7
8>7
8
7
6<7
Слайд 36Сортировка Шелла
4
1
6
3 шаг. 1 группа из 8-ми элементов
Массив отсортирован по возрастанию
по
12
14
9
8
7
1<6
6>4
6
4
1<4
6<7
4<6
7<12
12>8
8
12
7<8
12<14
8<12
14>9
9
14
12>9
9
12
8<9
Слайд 37Пусть нужно отсортировать массив А по возрастанию, в котором N элементов
Вспомогательные переменные
j – номер первого элемента остатка.
i – номер перемещаемого элемента.
M- оптимальный шаг
P– промежуточное значение, используемое для перемещения элементов массива
Постановка задачи
Слайд 38Начало алгоритма.
Шаг 1. M=целая часть N/2
Шаг 2. Пока M0 выполнять
Шаг
Шаг 2.2. Пока i<=N выполнять
Шаг 2.2.1. P=A[i]
Шаг 2.2.2. j=i-M
Шаг 2.2.3. Пока j>0 и P
Шаг 2.2.4. A[j+M]=P
Шаг 2.2.5. i=i+1
Шаг 2.3. M=целая часть M/2
Конец алгоритма.
Слайд 39Начало алгоритма.
Шаг 1. M=целая часть N/2
Шаг 2. Пока M0 выполнять
Шаг
Шаг 2.2. Пока i<=N выполнять
Шаг 2.2.1. P=A[i]
Шаг 2.2.2. j=i-M
Шаг 2.2.3. Пока j>0 и P
Шаг 2.2.4. A[j]=P
Шаг 2.2.5. i=i+1
Шаг 2.3. M=целая часть M/2
Конец алгоритма.
Определение максимальной величины шага
Определение первого и последнего элемента сравнения для текущего шага
Сортировка элементов последовательности
Определение нового шага сравнения
Определение первого и последнего элемента сравнения для текущего шага
Слайд 40Зачем необходимо это действие?
Начало алгоритма.
Шаг 1. M=целая часть N/2
Шаг 2. Пока
Шаг 2.1. i:=M+1
Шаг 2.2. Пока i<=N выполнять
Шаг 2.2.1. P=A[i]
Шаг 2.2.2. j=i-M
Шаг 2.2.3. Пока j>0 и P
Шаг 2.2.4. A[j]=P
Шаг 2.2.5. i=i+1
Шаг 2.3. M=целая часть M/2
Конец алгоритма.
Слайд 41Зачем необходимо это действие?
Начало алгоритма.
Шаг 1. M=целая часть N/2
Шаг 2. Пока
Шаг 2.1. i:=M+1
Шаг 2.2. Пока i<=N выполнять
Шаг 2.2.1. P=A[i]
Шаг 2.2.2. j=i-M
Шаг 2.2.3. Пока j>0 и P
Шаг 2.2.4. A[j]=P
Шаг 2.2.5. i=i+1
Шаг 2.3. M=целая часть M/2
Конец алгоритма.
Слайд 42Почему условие выхода из цикла такое?
Начало алгоритма.
Шаг 1. M=целая часть N/2
Шаг
Шаг 2.1. i:=M+1
Шаг 2.2. Пока i<=N выполнять
Шаг 2.2.1. P=A[i]
Шаг 2.2.2. j=i-M
Шаг 2.2.3. Пока j>0 и P
Шаг 2.2.4. A[j]=P
Шаг 2.2.5. i=i+1
Шаг 2.3. M=целая часть M/2
Конец алгоритма.
Слайд 44Придумана Ч.А.Р. Хоаром (Charles Antony Richard Hoare);
В основе – сортировка обменами;
Основана
Слайд 45Суть сортировки:
Выбирается некоторое значение (x)- барьерный элемент, который определяется округлением до
Просматриваем массив, двигаясь слева направо, пока не найдется элемент, больший x
Затем просматриваем его справа налево, пока не найдется элемент, меньший x
Слайд 46Суть сортировки:
Меняем найденные элементы местами. В случае, если не найден наибольший
Дойдя до середины имеем 2 части массива;
Процесс продолжается для каждой части, пока массив не будет отсортирован
Слайд 47Быстрая сортировка
8
12
3
7
19
11
4
16
Барьерный элемент
4
3
7
8
12
3
4
Барьерный элемент
8
12
11
19
Барьерный элемент
12
19
16
19
8>7 переносим в правую часть, т. к.
16>7 не переносим, 4<7 поэтому меняем местами 4 и 8
12>7 переносим в правую часть, т. к. 16>7, 8>7,11>7, 19>7 не переносим,
7=7 поэтому меняем местами 7 и 12
4>3
Отсортиро-ванная часть
12>11 переносим в правую часть, т. к.
16>11 не переносим, 8<11
поэтому меняем местами 12 и 8
19>11 переносим в правую часть, т. к. 16>11, 12>11,не переносим,
11=11 поэтому меняем местами 11 и 19
Отсортированная часть
19>12 переносим в правую часть, т. к. 16>12,не переносим,
12=12 поэтому меняем местами 12 и 19
19>16
Массив отсортирован по возрастанию
по возрастанию
Слайд 48Пусть нужно отсортировать массив А по возрастанию, в котором n элементов
Вспомогательные переменные:
t –конечный элемент массива
m - начальный элемент массива
x – элемент относительно которого перемещаются все остальные элементы.
w – промежуточное значение, используемое для перемещения элементов массива
Постановка задачи
Слайд 49Начало алгоритма.
Шаг 1 i=m j=t
Шаг 2 x=A[округление до целого(m+t)/2]
Шаг 3 Пока
Шаг 3.1 Если A[i]
Если A[j]>x то j:=j-1
иначе
w:=A[i]; A[i]:=A[j]; A[j]:=w
i:=i+1, j:=j-1
Шаг 4 Если m
Рекурсивный вызов процедуры
Слайд 50Начало алгоритма.
Шаг 1 i=m j=t
Шаг 2 x=A[округление до целого(m+t)/2]
Шаг 3 Пока
Шаг 3.1 Если A[i]
Если A[j]>x то j:=j-1
иначе
w:=A[i]; A[i]:=A[j]; A[j]:=w
i:=i+1, j:=j-1
Шаг 4 Если m
Зачем необходимо это действие?
Слайд 51Начало алгоритма.
Шаг 1 i=m j=t
Шаг 2 x=A[округление до целого(m+t)/2]
Шаг 3 Пока
Шаг 3.1 Если A[i]
Если A[j]>x то j:=j-1
иначе
w:=A[i]; A[i]:=A[j]; A[j]:=w
i:=i+1, j:=j-1
Шаг 4 Если m
Если исключить условие и просто вызвать процедуру, что может произойти?
Слайд 52Начало алгоритма.
Шаг 1 i=m j=t
Шаг 2 x=A[округление до целого(m+t)/2]
Шаг 3 Пока
Шаг 3.1 Если A[i]
Если A[j]>x то j:=j-1
иначе
w:=A[i]; A[i]:=A[j]; A[j]:=w
i:=i+1, j:=j-1
Шаг 4 Если m
Если изменить условие цикла на i
Слайд 53Начало алгоритма.
Шаг 1 i=m j=t
Шаг 2 x=A[округление до целого(m+t)/2]
Шаг 3 Пока
Шаг 3.1 Если A[i]
Если A[j]>x то j:=j-1
иначе
w:=A[i]; A[i]:=A[j]; A[j]:=w
i:=i+1, j:=j-1
Шаг 4 Если m
Что происходит в выделенном фрагменте?
Слайд 54Начало алгоритма.
Шаг 1 i=m j=t
Шаг 2 x=A[округление до целого(m+t)/2]
Шаг 3 Пока
Шаг 3.1 Если A[i]
Если A[j]>x то j:=j-1
иначе
w:=A[i]; A[i]:=A[j]; A[j]:=w
i:=i+1, j:=j-1
Шаг 4 Если m
Что происходит в выделенном фрагменте?
Слайд 55Начало алгоритма.
Шаг 1 i=m j=t
Шаг 2 x=A[округление до целого(m+t)/2]
Шаг 3 Пока
Шаг 3.1 Если A[i]
Если A[j]>x то j:=j-1
иначе
w:=A[i]; A[i]:=A[j]; A[j]:=w
i:=i+1, j:=j-1
Шаг 4 Если m
Что происходит с равными элементами?
Слайд 57Параметры оценки алгоритмов
Время сортировки - основной параметр, характеризующий быстродействие алгоритма
Память – выделяется ли дополнительная память под временное хранение данных
Слайд 58Устойчивость – отсортированный массив не меняет порядок элементов с одинаковыми значениями.
Взаимное
не изменилось
изменилось
Параметры оценки алгоритмов
Слайд 59 Естественность поведения - эффективность метода при обработке уже отсортированных, или
Параметры оценки алгоритмов
Слайд 60Оценка алгоритма сортировки выбором
Общее количество сравнений
C =N-l +
Общее количество операций n + (n-1) + (n-2) + (n-3) + ... + 1 = 1/2 * ( n2+n ) = Theta(n2)
Число обменов < числа сравнений = время сортировки растет квадратично относительно количества элементов
Слайд 62Если входная последовательность почти упорядочена, то сравнений будет столько же
алгоритм ведет
Слайд 63Оценка алгоритма сортировки вставкой
Для массива 1 2 3 4 5 6
Для массива 8 7 6 5 4 3 2 1 потребуется (N2-N)/2 сравнение.
Общее количество операций Theta(n2)
Слайд 65Наименьшие оценки эффективности, когда элементы предварительно упорядочены, а наибольшие – когда
алгоритм ведет
себя естественно
Слайд 66Не эффективный метод, так как включение элемента связано со сдвигом всех
В совокупности устойчивость и естественность поведения алгоритма, делает метод хорошим выбором в соответствующих ситуациях
Слайд 67Оценка алгоритма сортировки обменом
Количество сравнений
(n2-n)/2
Общее количество операций
Theta(n2)
Слайд 68Ответьте на следующие вопросы:
Устойчив ли этот метод?
Естественное ли поведение этого алгоритма?
Слайд 69Очень медленен и малоэффективен.
На практике, даже с улучшениями, работает, слишком
Прост, и его можно улучшать
Слайд 70Сравнение методов простой сортировки
N – количество элементов,
M – кол-во пересылок,
C – кол-во сравнений
?
Чему будет равно количество пересылок
Слайд 71Выбор метода сортировки
При сортировке маленьких массивов (менее 100 элементов) лучше использовать
Если известно, что список уже почти отсортирован, то подойдет любой метод;
Слайд 72Оценка алгоритма Шелла
Время выполнения пропорционально n1.2, т. к. при каждом проходе
Слайд 73Оценка алгоритма быстрой сортировки
Если размер массива равен числу, являющемуся степенью двойки
C=N+2*(N/2)+4*(N/4)+...+N*(N/N).
Если N не является степенью двойки, то оценка будет иметь тот же порядок
Слайд 74Общее количество операций Theta(n).
Количество шагов деления (глубина рекурсии) составляет приблизительно
Если каждый раз в качестве центрального элемента выбирается максимум или минимум входной последовательности, тогда быстродействие O(n2)
Слайд 75Метод неустойчив.
Поведение довольно естественно, если учесть, что при частичной упорядоченности
Сортировка использует дополнительную память
Слайд 76Итоги:
Предпочтительным является метод прямого включения;
Сортировка методом простого обмена является наихудшей;
Быстрая сортировка
Слайд 77Контрольные вопросы
Что такое «сортировка»?
В чем заключается метод сортировки отбором?
В чем заключается
В чем заключается метод пузырьковой сортировки?
В чем заключается метод быстрой сортировки?
В чем заключается метод сортировки Шелла?
Слайд 78Контрольные вопросы
Какой алгоритм сортировки считается самым простым?
Какой алгоритм сортировки считается самым
Сколько существует групп алгоритмов сортировки?
По каким признакам характеризуются алгоритмы сортировки?
Что нужно учитывать при выборе алгоритма сортировки?







![Начало алгоритма.Шаг 1 j:=2,Шаг 2 Пока j=2 и f=0 выполнять: Шаг 2.2.1 Если A[i-1]>A[i] то](/img/tmb/3/275819/4089ecfee744947f93358177a0486606-800x.jpg)
![Начало алгоритма.Шаг 1 j:=2,Шаг 2 Пока j=2 и f=0 выполнять: Шаг 2.2.1 Если A[i-1]>A[i] то](/img/tmb/3/275819/342b6c10389fdb1520dfea94667d4e14-800x.jpg)
![Начало алгоритма.Шаг 1 j:=2,Шаг 2 Пока j=2 и f=0 выполнять: Шаг 2.2.1 Если A[i-1]>A[i] то](/img/tmb/3/275819/e90ae1695bc7eaddc24b8472e8d81a99-800x.jpg)
![Начало алгоритма.Шаг 1 j:=2,Шаг 2 Пока j=2 и f=0 выполнять: Шаг 2.2.1 Если A[i-1]>A[i] то](/img/tmb/3/275819/6780de3bb48ba4913a1ebd91cdb75f78-800x.jpg)
![Начало алгоритма.Шаг 1 j:=2,Шаг 2 Пока j=2 и f=0 выполнять: Шаг 2.2.1 Если A[i-1]>A[i] то](/img/tmb/3/275819/474a9cef032864ee09759aadc99ccaf0-800x.jpg)
![Начало алгоритма.Шаг 1 j:=2,Шаг 2 Пока j=2 и f=0 выполнять: Шаг 2.2.1 Если A[i-1]>A[i] то](/img/tmb/3/275819/23b40efccd420539332723909e213431-800x.jpg)
![Начало алгоритма.Шаг 1 j:=2,Шаг 2 Пока j=2 и f=0 выполнять: Шаг 2.2.1 Если A[i-1]>A[i] то](/img/tmb/3/275819/307dd41f98f8782c3561929fb98c74c8-800x.jpg)











![Начало алгоритма.Шаг 1 j:=N,Шаг 2 Пока j>=2 выполнять: Шаг 2.1 i:=1; , Шаг 2.2 Пока iA[i+1]](/img/tmb/3/275819/9791ef68f5f5e51661cfd600b451f25b-800x.jpg)
![Начало алгоритма.Шаг 1 j:=N,Шаг 2 Пока j>=2 выполнять: Шаг 2.1 i:=1; , Шаг 2.2 Пока iA[i+1]](/img/tmb/3/275819/e42ddd44fd28ad48924f1606ab34ee35-800x.jpg)
![Начало алгоритма.Шаг 1 j:=N,Шаг 2 Пока j>=2 выполнять: Шаг 2.1 i:=1; , Шаг 2.2 Пока iA[i+1]](/img/tmb/3/275819/bd03dca02953337c15d9c640b38e158b-800x.jpg)


















![Начало алгоритма.Шаг 1 i=m j=tШаг 2 x=A[округление до целого(m+t)/2]Шаг 3 Пока i](/img/tmb/3/275819/5b6d6f4f654e3a7c6f7e65fe9a3c4c4b-800x.jpg)
![Начало алгоритма.Шаг 1 i=m j=tШаг 2 x=A[округление до целого(m+t)/2]Шаг 3 Пока i](/img/tmb/3/275819/189e712bba62f45bbb83bfb5e6b49ee8-800x.jpg)
![Начало алгоритма.Шаг 1 i=m j=tШаг 2 x=A[округление до целого(m+t)/2]Шаг 3 Пока i](/img/tmb/3/275819/13f2c56b036688e9dc1c13fa7fdacdd4-800x.jpg)
![Начало алгоритма.Шаг 1 i=m j=tШаг 2 x=A[округление до целого(m+t)/2]Шаг 3 Пока i](/img/tmb/3/275819/fd354bc7ed7bd5a88f5b9a9ec7ab7490-800x.jpg)
![Начало алгоритма.Шаг 1 i=m j=tШаг 2 x=A[округление до целого(m+t)/2]Шаг 3 Пока i](/img/tmb/3/275819/ec337094c773b7363318590ef215d35e-800x.jpg)
![Начало алгоритма.Шаг 1 i=m j=tШаг 2 x=A[округление до целого(m+t)/2]Шаг 3 Пока i](/img/tmb/3/275819/64bed3e2b402b93bb9ca7af5fb0f3f1a-800x.jpg)
![Начало алгоритма.Шаг 1 i=m j=tШаг 2 x=A[округление до целого(m+t)/2]Шаг 3 Пока i](/img/tmb/3/275819/dcb45810b16b5dbc15e2ec8033eb4ccc-800x.jpg)