- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические модели в расчетах на ЭВМ презентация
Содержание
- 1. Математические модели в расчетах на ЭВМ
- 2. Общая характеристика математических методов для инженерных
- 3. Задачи, решаемые с помощью математических моделей, заложенных
- 4. Математические модели - являются основой математического обеспечения
- 5. Математическое обеспечение АИС или САПР
- 6. Математические модели: основные понятия Под математической моделью
- 7. Математические модели: основные понятия Структура ММ –
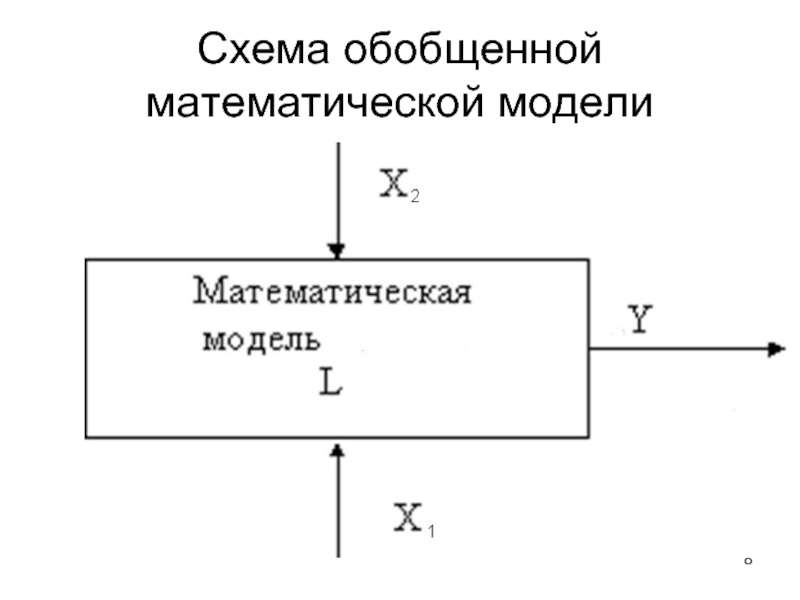
- 8. Схема обобщенной математической модели
- 9. Данные математических моделей X (X1,X2,…) - множество
- 10. Математическое моделирование по статистическим или экспериментальным
- 11. Входные данные математических моделей Множество независимых переменных
- 12. Методы получения математических моделей Получение математических моделей
- 13. Теоретические методы разработки ММ - основаны
- 14. Экспериментальные методы разработки ММ - методы основаны
- 15. Порядок разработки ММ 1. Выбор свойств объекта,
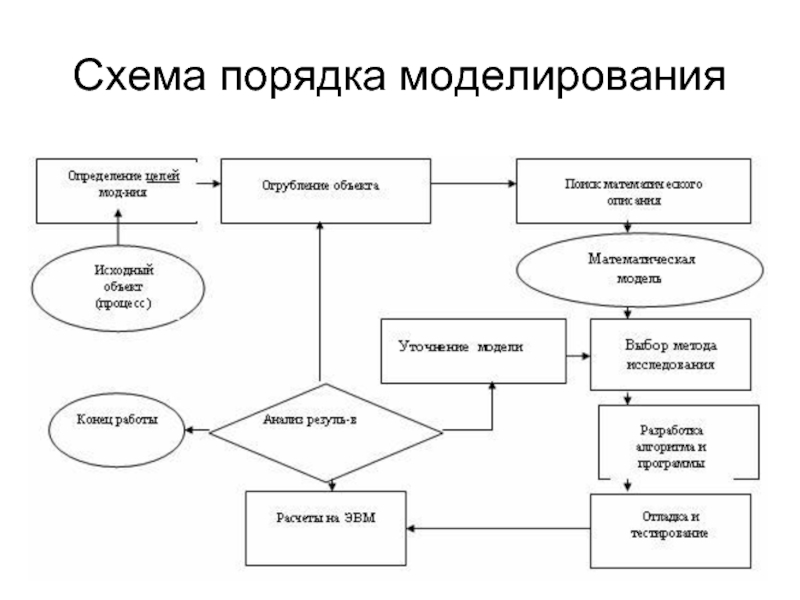
- 16. Схема порядка моделирования
- 17. Цели моделирования ММ нужна для того, чтобы
- 18. Примеры целей моделирования Какой режим эксплуатации технического
- 19. Программное обеспечение ЭВМ, используемое на различных этапах
- 20. Программное обеспечение ЭВМ, используемое на различных этапах
- 21. SMathStudio программа для проведения математических вычислений и
- 22. EXCEL Использование именно Excel в качестве средства
- 23. Регрессионные математические модели Регрессионные ММ применяются для
- 24. Примеры регрессионных математических моделей Пример 1. Запись
- 25. Пример 2. Запись ММ в виде формулы
- 26. Примеры математических моделей Пример 3. Запись ММ
- 27. Примеры математических моделей 3.3. Степенная – y(x)=a▪x
- 28. Математические модели определяются по экспериментальным или
- 29. Ранжирование факторов х 1. для
- 30. Пример 1. Ранжирование факторов х по коэффициенту
- 31. Пример 2. Ранжирование факторов х экспертами
- 32. Неизвестные а, b, c и т.п.
- 33. Проверка регрессионных математических моделей Проверка правильности ММ
- 34. Нахождение коэффициентов линейной ММ в EXCEL 1.
- 35. Нахождение коэффициентов линейной ММ в EXCEL
- 36. Нахождение коэффициентов линейной ММ в EXCEL
- 37. Нахождение коэффициентов линейной ММ в EXCEL 7.
- 38. Нахождение коэффициентов линейной ММ в EXCEL
- 39. Нахождение коэффициентов линейной ММ в EXCEL
- 40. Нахождение коэффициентов линейной ММ в EXCEL
- 41. Нахождение коэффициентов линейной ММ в EXCEL Так
- 42. Метод наименьших квадратов (МНК) в матричной форме
- 43. Применение МНК в MathCAD
- 44. Применение МНК в SmathStudio Как видно из
- 45. Определение коэффициентов нелинейных однофакторных математических моделей Дана
- 46. Пример определения коэффициентов нелинейных однофакторных математических моделей
- 47. Пример определения коэффициентов нелинейных однофакторных математических моделей
- 48. Пример определения коэффициентов нелинейных однофакторных математических моделей в Excel методом линеаризации
- 49. Пример определения коэффициентов нелинейных однофакторных математических моделей
- 50. Пример определения коэффициентов нелинейных однофакторных математических моделей
- 51. Пример определения коэффициентов нелинейных однофакторных математических моделей
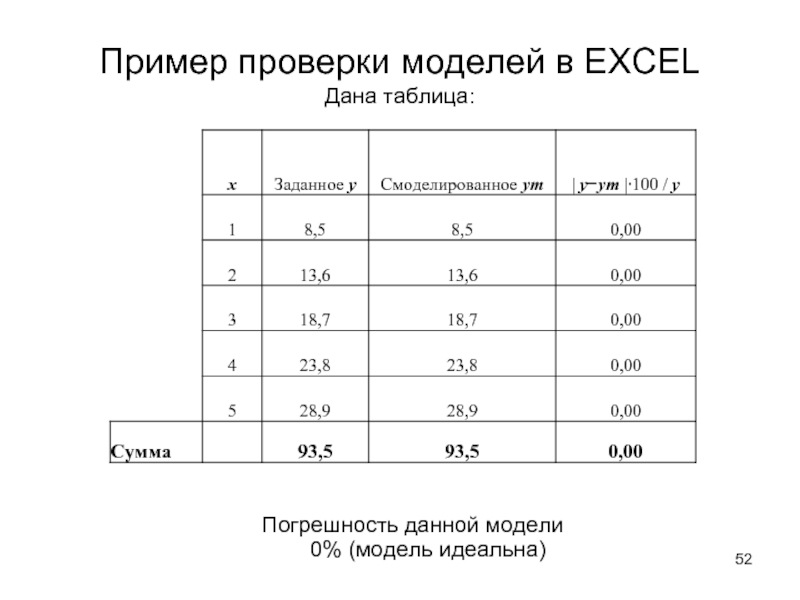
- 52. Пример проверки моделей в EXCEL Дана таблица: Погрешность данной модели 0% (модель идеальна)
- 53. Фиктивные переменные в моделях Переменные Х могут
- 54. Регрессионные математические модели могут быть объединены в
- 55. Аналитические математические модели в виде системы уравнений/неравенств
- 56. Формулировка задачи линейного программирования (ЗЛП) Реализуются линеаризованные
- 57. Пример решения задачи линейного программирования Постановка задачи.
- 58. Решение задачи линейного программирования 1. Неравенства (1)…(3)
- 59. Решение задачи линейного программирования 4.Находят точки пересечения
- 60. Рассмотрим еще примеры применения математических моделей различных форм и записей
- 61. Пример записи ММ в виде табличного алгоритма
- 62. 1. Составляется комплекс условий применимости (КУП) для
- 63. Пример разработки ММ в аналитической форме и
- 64. Пример разработки ММ в аналитической форме и
- 65. ММ в виде блок-схемы
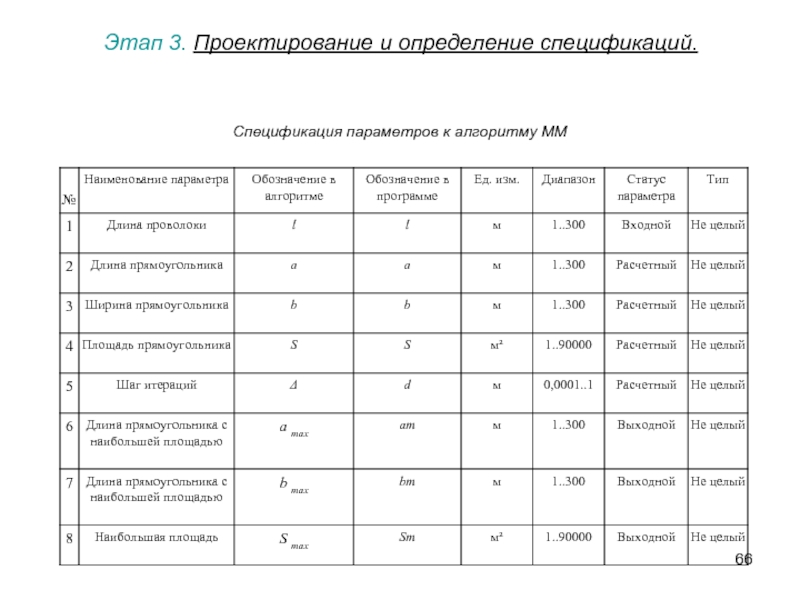
- 66. Этап 3. Проектирование и определение спецификаций. Спецификация параметров к алгоритму ММ
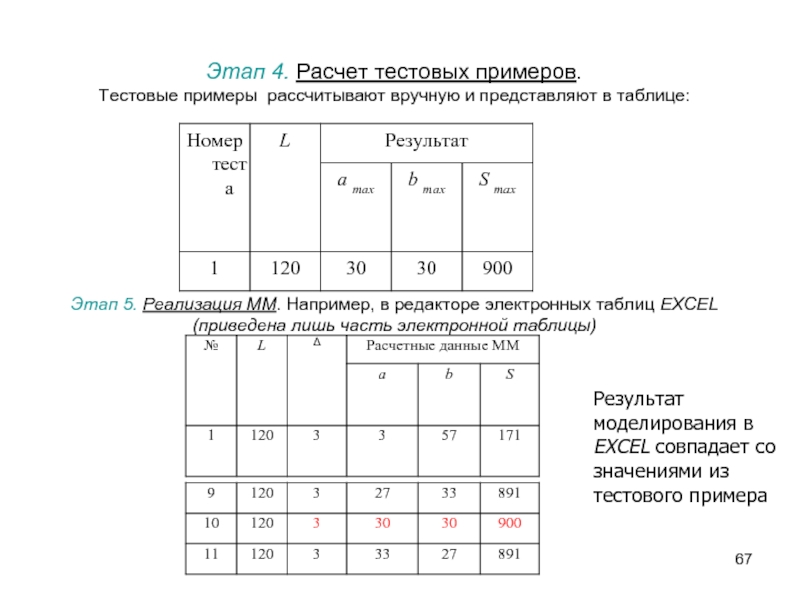
- 67. Этап 4. Расчет тестовых примеров. Тестовые примеры
- 68. Многокритериальные ММ В предыдущих примерах мы рассматривали
- 69. Комплексная целевая функция моделирования где m –
- 70. Пример использования комплексной оценки Задача: Требуется оценить
- 71. Пример использования комплексной оценки Результаты расчета Для
- 72. Спасибо за внимание ☺ Следующие занятия будут
Слайд 1«Математические модели в расчетах на ЭВМ»
Основное содержание курса лекций и
Преподаватель: к.т.н., доцент Уразбахтина Анжелика Юрьевна
2016 г
Слайд 2
Общая характеристика математических методов для инженерных расчетов на ЭВМ
Применение математических методов
Автоматизация проектирования особенно эффективна, когда от автоматизации выполнения отдельных инженерных расчетов переходят к использованию автоматизированных информационных систем (АИС) или систем автоматизированного проектирования (САПР).
Слайд 3Задачи, решаемые с помощью математических моделей, заложенных в АИС или САПР:
Моделирование и мониторинг разработки месторождений;
Информационные технологии в проектировании объектов обустройства месторождений;
Стандартизация и техническое регулирование;
Комплексные решения для корпоративных информационных систем;
Моделирование последствий экологических катастроф.
Слайд 4Математические модели -
являются основой математического обеспечения (МО) САПР или АИС.
Слайд 5Математическое обеспечение АИС или САПР
Математическое обеспечение
Слайд 6Математические модели: основные понятия
Под математической моделью (ММ) объекта и его элементов
При построении ММ используют различные математические средства описания объекта – теорию множеств, графов, вероятностей, математическую логику, математическое программирование, дифференциальные или интегральные уравнения и т.д.
Слайд 7Математические модели: основные понятия
Структура ММ – общий вид математических отношений модели
Математическая модель описывает зависимость между исходными (входными) данными и искомыми величинами.
Слайд 9Данные математических моделей
X (X1,X2,…) - множество входных данных (факторов, независимых переменных),
L - математический оператор, определяющий операции над входными данными; это полная система математических операций, описывающих численные или логические соотношения между множествами входных и выходных данных;
Y - множество выходных данных (зависимых переменных); представляет собой совокупность критериев оценки моделируемого объекта или целевых функций улучшения объекта.
Слайд 10Математическое моделирование
по статистическим или экспериментальным данным называется аппроксимацией или регрессионным
Цели регрессионного анализа: определить силу влияния факторов X (X1,X2,…) на результат Y и найти неизвестные коэффициенты математической модели а,b,c и т.д.
При этом используются методы замены для преобразования нелинейных функций в линейные.
Слайд 11Входные данные математических моделей
Множество независимых переменных (констант) из числа X (X1,X2,…)
Это могут быть:
технические параметры объекта, не подлежащие изменению в процессе проектирования;
физические возмущения среды, с которой взаимодействует объект проектирования;
тактические параметры, которые должен достигать объект проектирования.
Разделение входных параметров X (X1,X2,…) по степени важности влияния их изменений на выходные данные Y называется ранжированием.
Слайд 12Методы получения математических моделей
Получение математических моделей (ММ) - процедура неформализованная, т.е.
Разработка ММ обычно выполняется специалистами конкретных областей с помощью традиционных экспериментальных исследований.
Методы получения математических моделей делят на теоретические и экспериментальные.
Слайд 13Теоретические методы разработки ММ -
основаны на изучении физических закономерностей протекающих
Слайд 14Экспериментальные методы разработки ММ -
методы основаны на использовании внешних проявлений свойств
Слайд 15Порядок разработки ММ
1. Выбор свойств объекта, которые подлежат отражению в модели.
2. Сбор исходной информации о выбранных свойствах объекта (входной, выходной информации. Источниками ее являются: опыт и знания человека, разрабатывающего модель; содержание научно-технической литературы; описания прототипов – имеющихся ММ для элементов, близких по своим свойствам к исследуемому; результаты экспериментального измерения параметров и т.п.
3. Синтез структуры ММ в виде алгоритма, блок-схемы, аналитической формы, матрицы решения. Синтез структуры – это поиск и упорядочивание аналитических, логических и других зависимостей для преобразования входных параметров в выходные.
4. Расчет числовых значений параметров ММ (разработка тестового или контрольного примера). На этом этапе решается задача минимизации погрешности математической модели.
5. Оценка точности и адекватности ММ. Здесь устанавливается степень расхождения с тестовым примеров или с реальным объектом.
6. Разработка и оформление документации к ММ завершает ее проектирование.
Слайд 17Цели моделирования
ММ нужна для того, чтобы понять, как устроен конкретный объект,
ММ нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);
ММ нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).
Слайд 18Примеры целей моделирования
Какой режим эксплуатации технического объекта выбрать для того, чтобы
2. Как составить график выполнения сотен видов взаимозависимых работ на объекте, чтобы они закончились в максимально короткие сроки?
3. Проследить (предсказать) экологические и климатические последствия прорыва крупного нефтепровода.
4. Проследить (предсказать) социальные последствия изменений цен на нефть.
Слайд 19Программное обеспечение ЭВМ, используемое на различных этапах математического моделирования
Пакет MATLAB
Система
Используя пакет MATLAB можно как из кубиков построить довольно сложную математическую модель, или написать свою программу.
Слайд 20Программное обеспечение ЭВМ, используемое на различных этапах математического моделирования
MATHCAD
Универсальный математический пакет,
Ориентирован на естественный математический язык и “непрограммирующего пользователя”.
Пакет объединяет в себе: редактор математических формул, интерпретатор для вычислений, библиотеку математических функций, процессор символьных преобразований, текстовый редактор, графические средства представления результатов, возможности структурного программирования.
Слайд 21SMathStudio
программа для проведения математических вычислений и построения графиков, позволяет работать с
Поддерживается использование примитивного программирования - циклов FOR и WHILE, условий IF и т.д. Пользователь программы имеет возможность быстрой вставки единиц измерения, может экспортировать созданные проекты в форматы HTML и MathCad или сохранять их в виде изображений BMP, GIF, JPG и PNG.
В SMathStudio есть встроенный справочник, посвященный тригонометрии, логарифмам, производным, пределам и прочим математическим понятиям.
Также в программе имеется коллекция примеров по решению математических задач.
Слайд 22EXCEL
Использование именно Excel в качестве средства разработки математических моделей оправдывается не
Модели, разрабатываемые на базе этого поистине «народного» инструмента, как правило, наиболее просты в освоении, и даже их самостоятельная адаптация к меняющимся условиям может быть для более или менее квалифицированных пользователей Excel вполне посильной задачей.
К тому же, на рабочих местах использование иных программных средств может оказаться затруднительным – хотя бы в силу ресурсных ограничений (это могут быть и устаревшие компьютеры, и отсутствие локальной сети, и низкая квалификация пользователей).
Слайд 23Регрессионные математические модели
Регрессионные ММ применяются для исследования зависимости изучаемой переменной Y
В регрессионных моделях зависимая (объясняемая) переменная Y может быть представлена в виде функции
где - независимые (объясняющие) переменные, или факторы.
ММ регрессии можно использовать не только для анализа, но и для прогнозирования явлений различной природы.
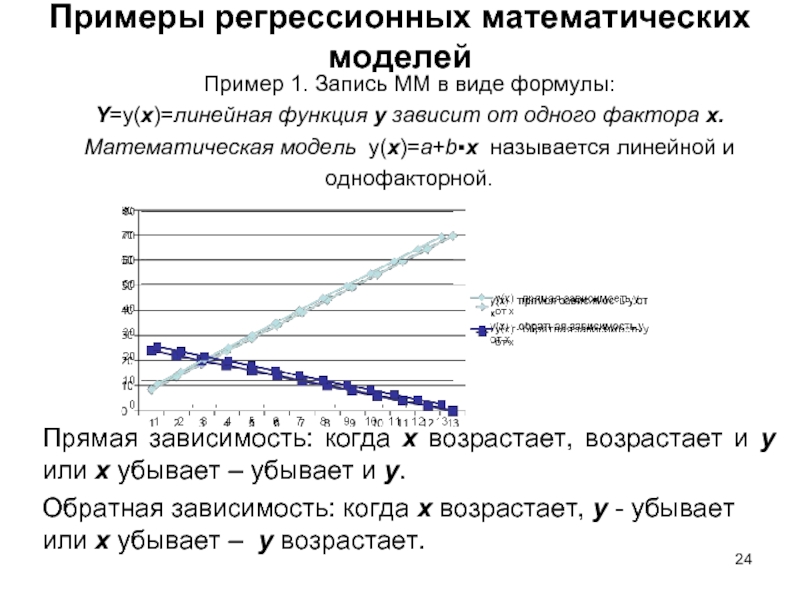
Слайд 24Примеры регрессионных математических моделей
Пример 1. Запись ММ в виде формулы:
Y=y(x)=линейная
Математическая модель у(х)=а+b▪x называется линейной и однофакторной.
Прямая зависимость: когда х возрастает, возрастает и у или х убывает – убывает и у.
Обратная зависимость: когда х возрастает, у - убывает или х убывает – у возрастает.
Слайд 25Пример 2. Запись ММ в виде формулы
y(x1,х2,…)= линейная функция у
Математическая модель у(х)=а+b ▪ x1+ с ▪ х2 + … называется линейной и многофакторной. Ее график и зависимости аналогичны однофакторной модели
Примеры математических моделей
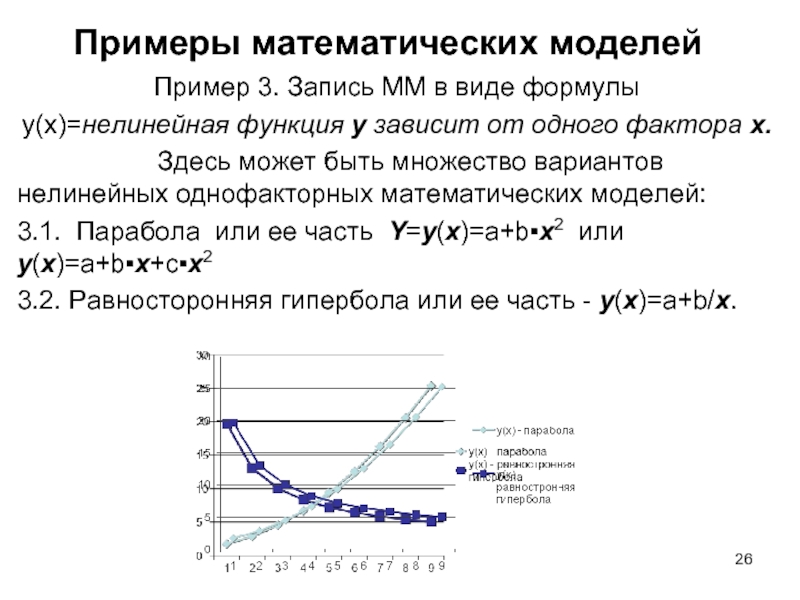
Слайд 26Примеры математических моделей
Пример 3. Запись ММ в виде формулы
y(x)=нелинейная функция
Здесь может быть множество вариантов нелинейных однофакторных математических моделей:
3.1. Парабола или ее часть Y=y(x)=a+b▪x2 или y(x)=a+b▪х+с▪x2
3.2. Равносторонняя гипербола или ее часть - y(x)=a+b/x.
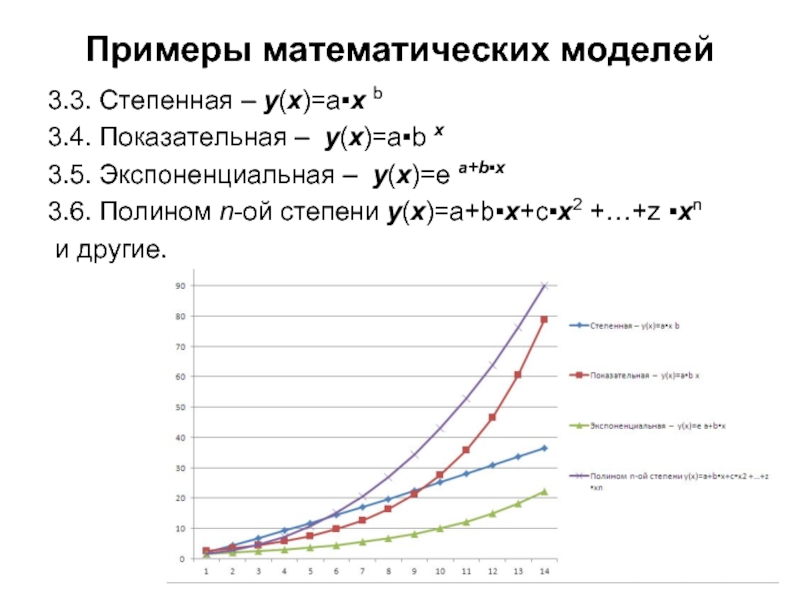
Слайд 27Примеры математических моделей
3.3. Степенная – y(x)=a▪x b
3.4. Показательная –
3.5. Экспоненциальная – y(x)=е а+b▪х
3.6. Полином n-ой степени y(x)=a+b▪х+с▪x2 +…+z ▪xn
и другие.
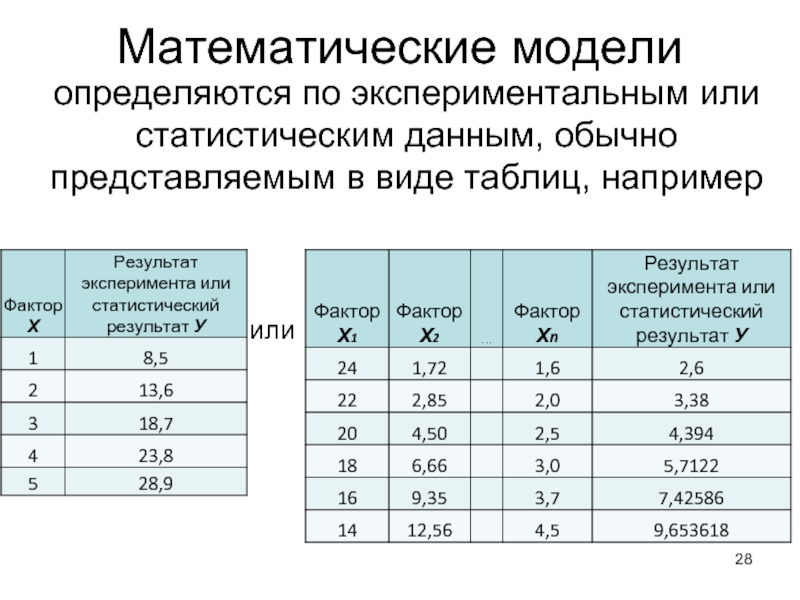
Слайд 28Математические модели
определяются по экспериментальным или статистическим данным, обычно представляемым в
или
Слайд 29Ранжирование факторов х
1. для линейных моделей можно производить по
2. по значимости фактора х для правильного функционирования объекта моделирования. Значимость устанавливается путем опроса экспертов в нефтегазодобывающей промышленности.
При разработке регрессионных математических моделей проводят ранжирование факторов (X1,X2,…) . В результате ранжирования определяется – будет ли фактор хi входить в модель или нет.
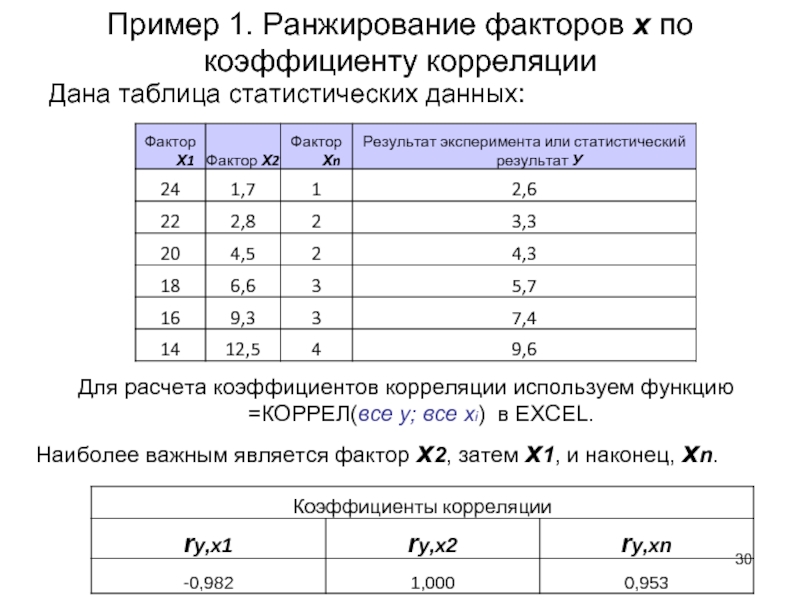
Слайд 30Пример 1. Ранжирование факторов х по коэффициенту корреляции
Дана таблица статистических данных:
Для
Наиболее важным является фактор х2, затем х1, и наконец, xn.
Слайд 32
Неизвестные а, b, c и т.п. математических моделей находятся с помощью
Слайд 33Проверка регрессионных математических моделей
Проверка правильности ММ заключается в разработке и проведении
визуальной проверке по графикам заданного у и смоделированного умм.
сравнении сумм заданного у и смоделированного умм.
Проверке, что ∑ (заданное у – смоделированное умм)2 → min.
определении относительной погрешности аппроксимации EОТН (%) по формуле
Относительная погрешность модели должны быть меньше 7%
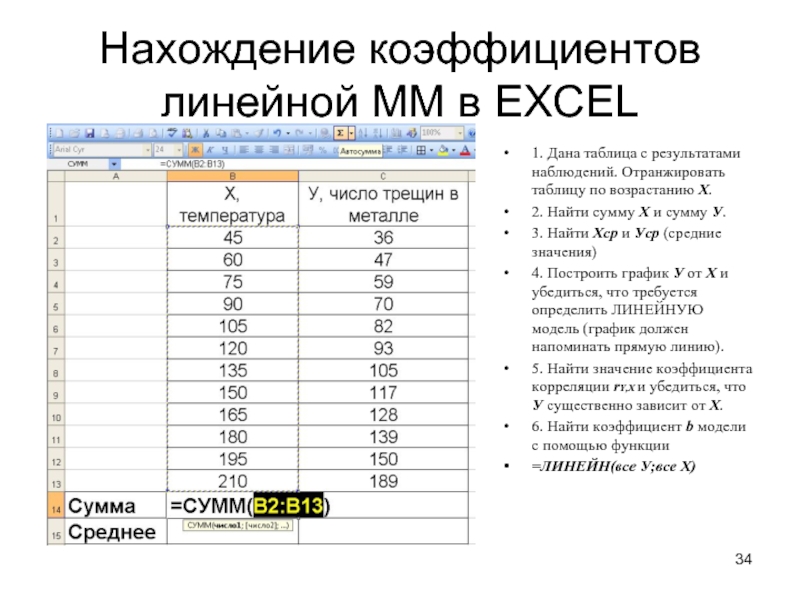
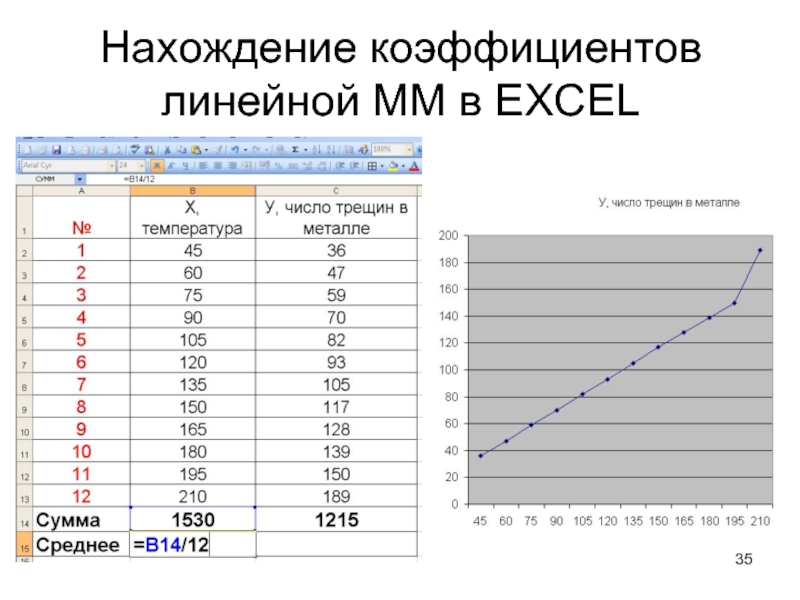
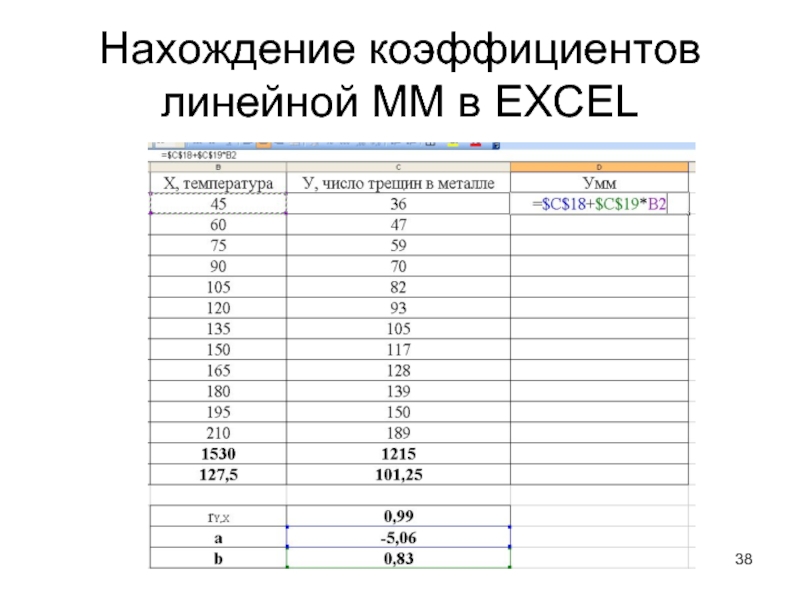
Слайд 34Нахождение коэффициентов линейной ММ в EXCEL
1. Дана таблица с результатами наблюдений.
2. Найти сумму Х и сумму У.
3. Найти Хср и Уср (средние значения)
4. Построить график У от Х и убедиться, что требуется определить ЛИНЕЙНУЮ модель (график должен напоминать прямую линию).
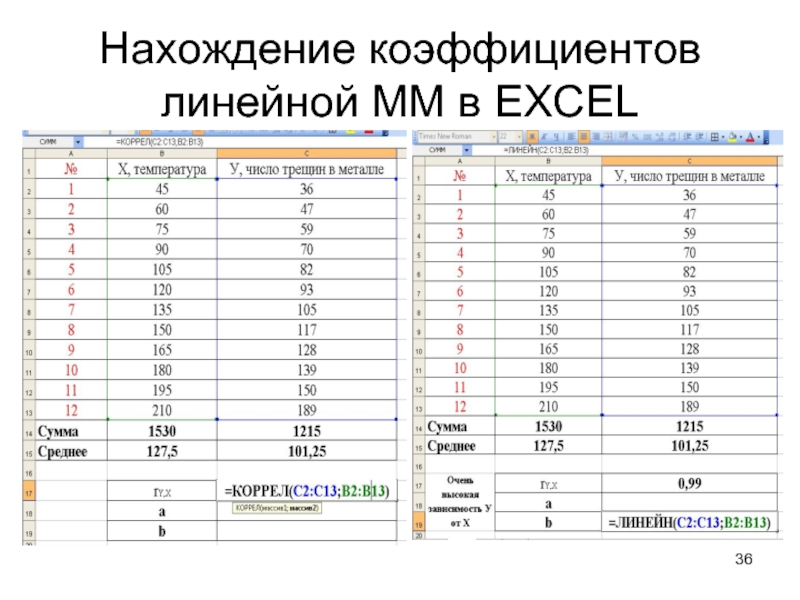
5. Найти значение коэффициента корреляции rY,X и убедиться, что У существенно зависит от Х.
6. Найти коэффициент b модели с помощью функции
=ЛИНЕЙН(все У;все Х)
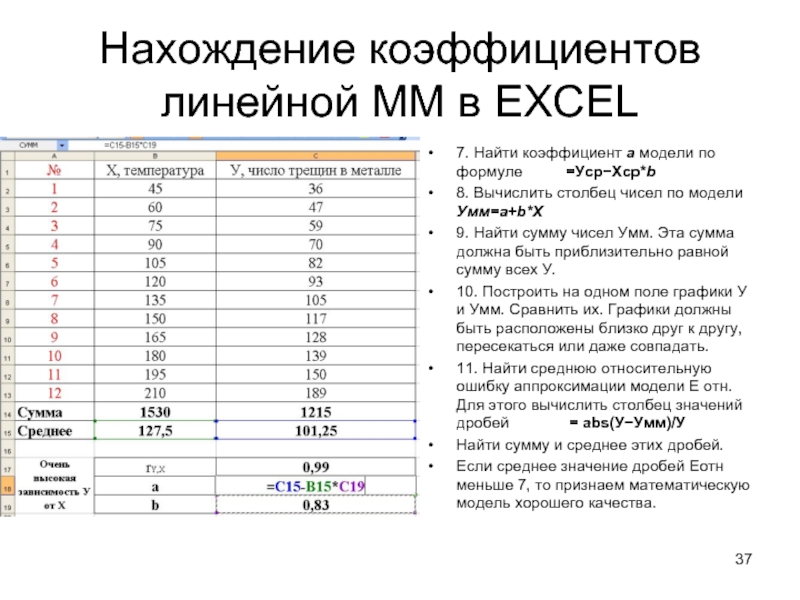
Слайд 37Нахождение коэффициентов линейной ММ в EXCEL
7. Найти коэффициент а модели по
8. Вычислить столбец чисел по модели Умм=a+b*X
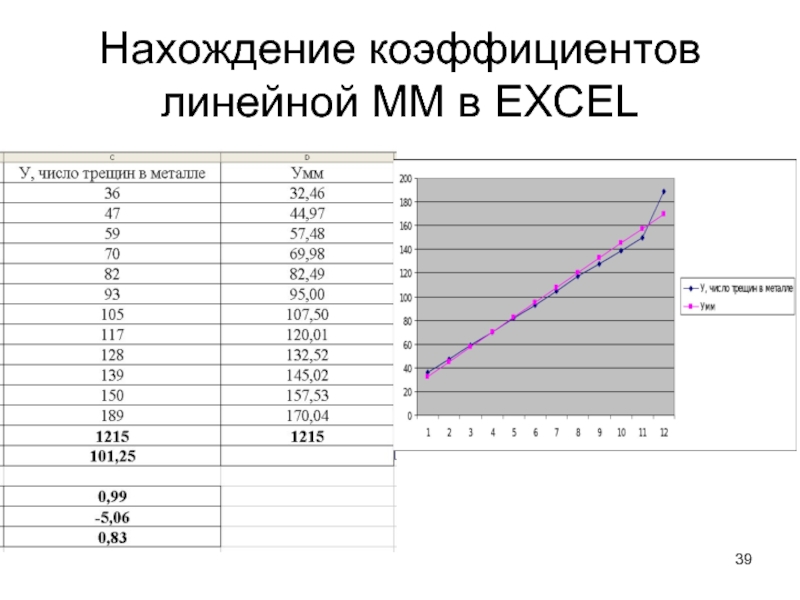
9. Найти сумму чисел Умм. Эта сумма должна быть приблизительно равной сумму всех У.
10. Построить на одном поле графики У и Умм. Сравнить их. Графики должны быть расположены близко друг к другу, пересекаться или даже совпадать.
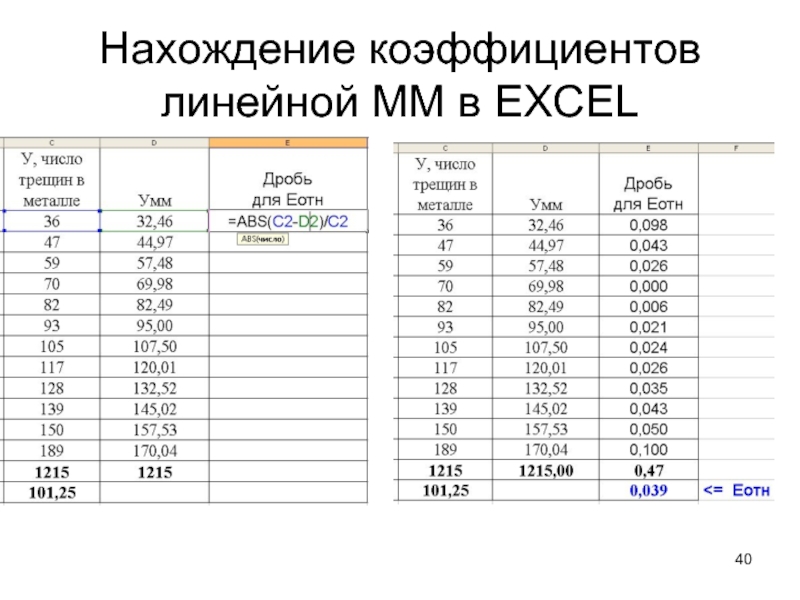
11. Найти среднюю относительную ошибку аппроксимации модели Е отн. Для этого вычислить столбец значений дробей = abs(У−Умм)/У
Найти сумму и среднее этих дробей.
Если среднее значение дробей Еотн меньше 7, то признаем математическую модель хорошего качества.
Слайд 41Нахождение коэффициентов линейной ММ в EXCEL
Так как Еотн=0,039 и существенно меньше
Слайд 42Метод наименьших квадратов (МНК) в матричной форме для определения коэффициентов регрессионных
матрица независимых факторов х, в первый столбец этой матрицы обязательно записываются только 1. Состав остальных столбцов зависит от предполагаемой математической формулы модели.
матрица результирующих значений процесса или работы производственной системы
где
Слайд 43Применение МНК в MathCAD
покажем на примере определения коэффициентов
Таким образом определили линейные математические модели 3,4+5,1⋅x и -4,796+0,176⋅x1+0,385⋅x2+1,585⋅xn
Слайд 44Применение МНК в SmathStudio
Как видно из примеров, результаты применения МНК не
Слайд 45Определение коэффициентов нелинейных однофакторных математических моделей
Дана таблица с экспериментальными данными.
Отранжируем все
Строим график у.
По графику убеждаемся, что функция ММ y(x) нелинейная.
Высказываем предположение, какая это функция (парабола, гипербола, степенная и т.д.)
Формируем матрицу Х в соответствии с выбранной нелинейной функцией.
Определяем коэффициенты модели.
Оцениваем точность модели.
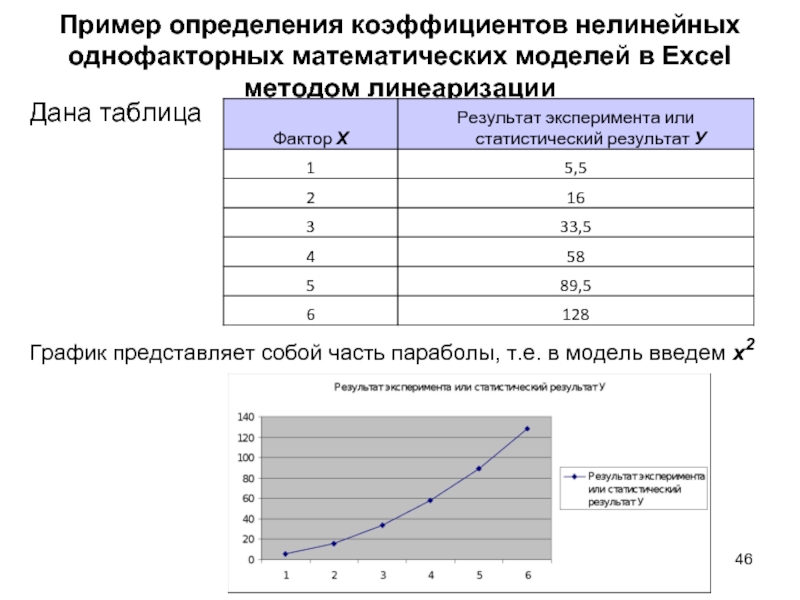
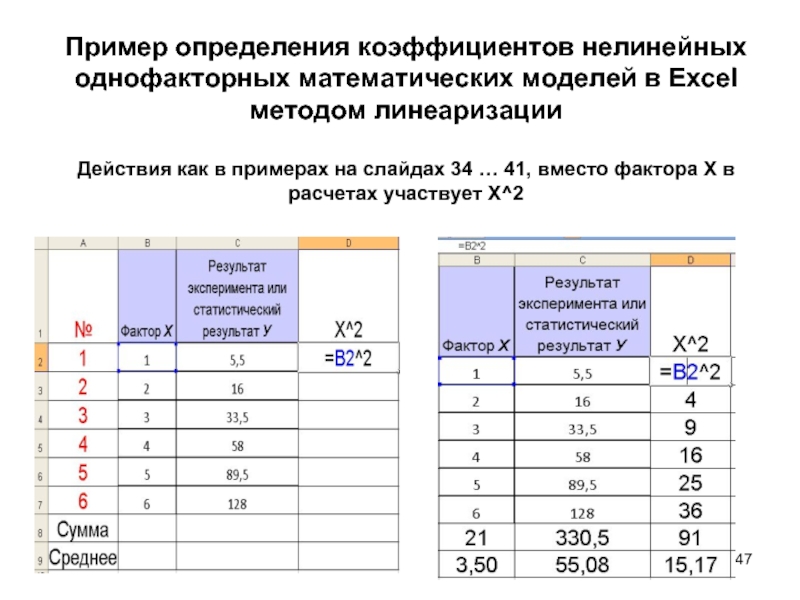
Слайд 46Пример определения коэффициентов нелинейных однофакторных математических моделей в Excel методом линеаризации
Дана
График представляет собой часть параболы, т.е. в модель введем x2
Слайд 47Пример определения коэффициентов нелинейных однофакторных математических моделей в Excel методом линеаризации Действия
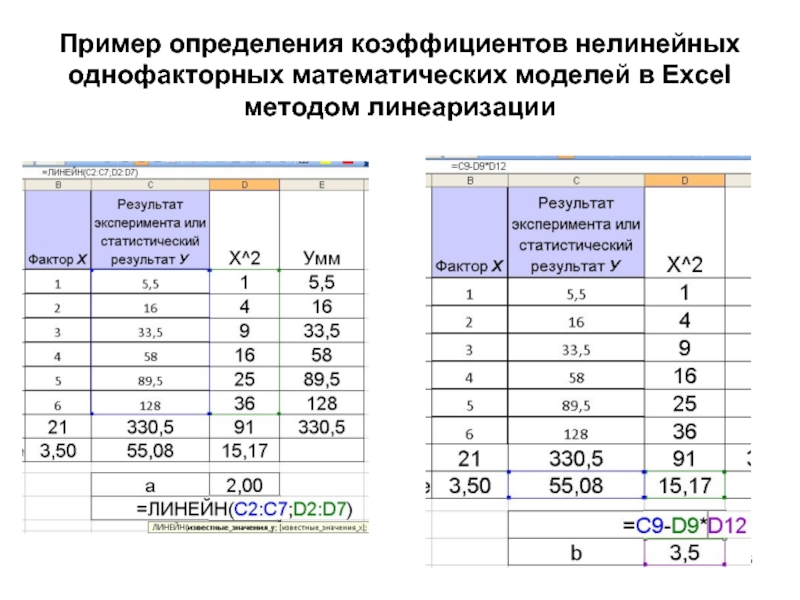
Слайд 48Пример определения коэффициентов нелинейных однофакторных математических моделей в Excel методом линеаризации
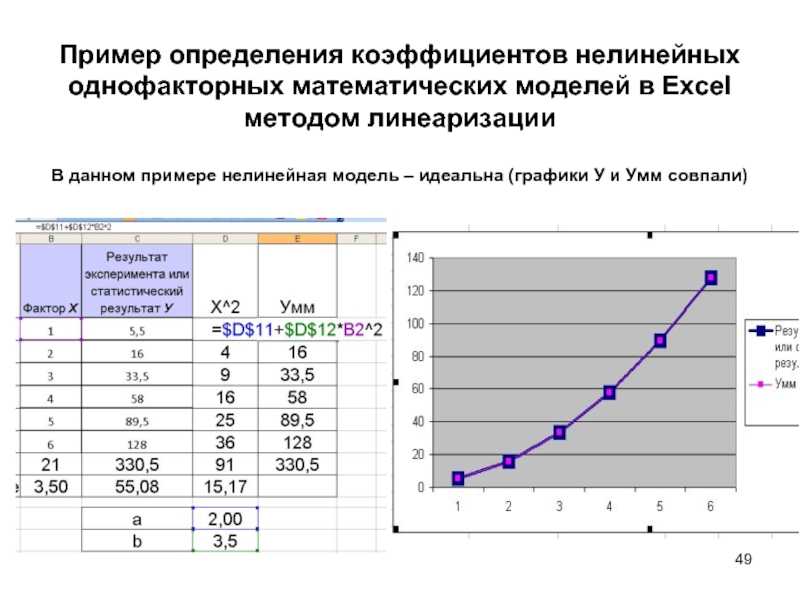
Слайд 49Пример определения коэффициентов нелинейных однофакторных математических моделей в Excel методом линеаризации В
Слайд 50Пример определения коэффициентов нелинейных однофакторных математических моделей в Excel
I. При линеаризации
вместо Х во всех расчетах используется дробь 1/Х.
II. Для степенных моделей при линеаризации используются натуральные логарифмы ln:
1) Y=a*bX
Ln(Y)=Ln(a*bX )=Ln(a)+Ln(bX )=Ln(a)+X*Ln(b),
2) Y=a*Xb
Ln(Y)=Ln(a*Xb )=Ln(a)+Ln(Xb )=Ln(a)+b*Ln(X),
и в расчетах участвуют столбцы чисел Ln(Y) и Ln(X)
Слайд 51Пример определения коэффициентов нелинейных однофакторных математических моделей в MathCAD
Первый столбец в ней заполняем 1, второй столбец заполняем значениями x2.
Применяем МНК.
Получаем коэффициенты модели.
Результат – математическая модель y(x)=2+3,5x2.
Слайд 53Фиктивные переменные в моделях
Переменные Х могут быть не только количественными (числами),
Например, Х=1 – вертикальное расположение; Х=0 – горизонтальное расположение.
Слайд 54Регрессионные математические модели могут быть объединены в системы, в которые включаются
Слайд 55Аналитические математические модели в виде системы уравнений/неравенств
Аналитические модели представляют собой явно
Пример линеаризованной аналитической математической модели:
ММ=
где
, - параметры моделируемого объекта;
− ограничения, накладываемые на функционирование объекта окружающей средой;
- целевая функция моделирования.
Слайд 56Формулировка задачи линейного программирования (ЗЛП)
Реализуются линеаризованные математические модели в виде систем
«Имеется некоторая величина, являющаяся линейной функцией ряда переменных, которые, в свою очередь, должны удовлетворять ограничениям, выраженным в виде системы линейных равенств или неравенств. Требуется отыскать такие неотрицательные значения переменных, удовлетворяющих системе ограничений, при которых величина, являющаяся их линейной функцией, принимала бы наименьшее или наибольшее значение.»
Слайд 57Пример решения задачи линейного программирования
Постановка задачи. Найти минимум целевой функции:
где х и y − объем добычи нефти и газа;
a и b − трудоемкость добычи нефти и газа;
- ограничение по количеству резервуаров;
- ограничение по количеству используемого оборудования;
- ограничение по количеству используемых месторождений.
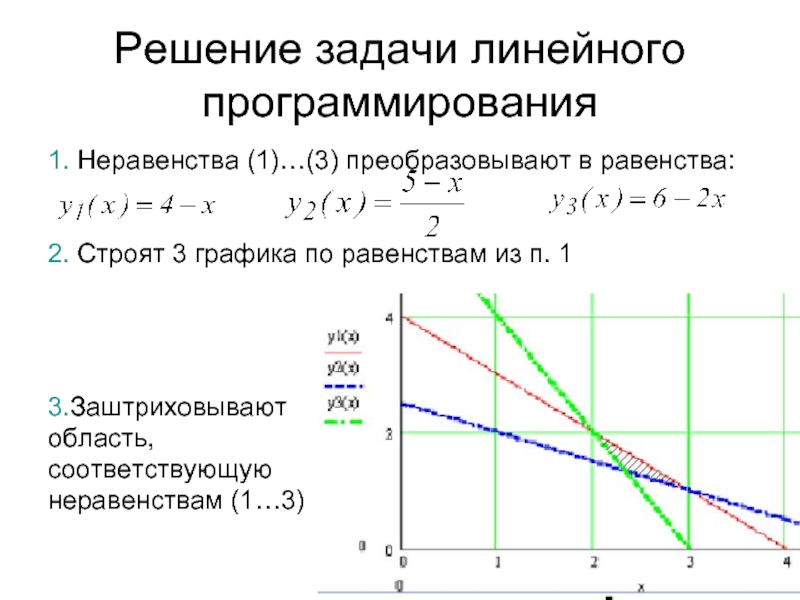
Слайд 58Решение задачи линейного программирования
1. Неравенства (1)…(3) преобразовывают в равенства:
2. Строят 3
3.Заштриховывают
область,
соответствующую
неравенствам (1…3)
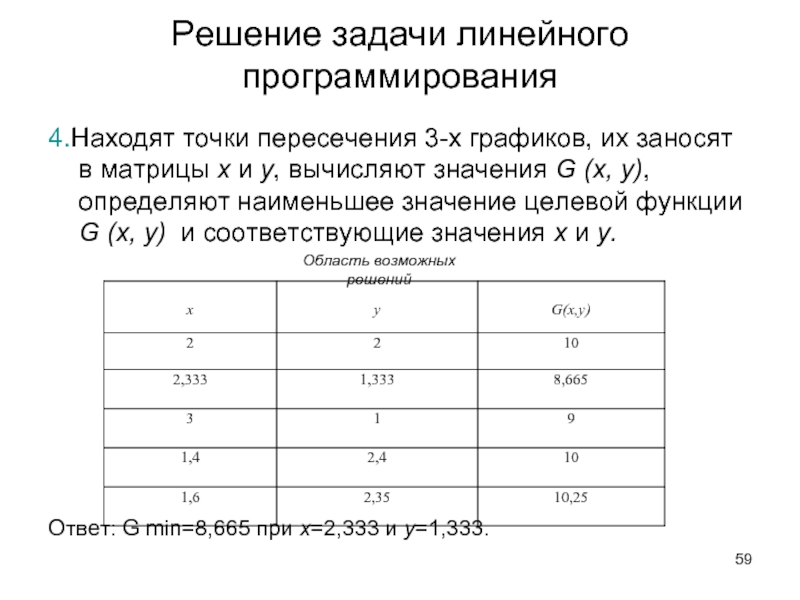
Слайд 59Решение задачи линейного программирования
4.Находят точки пересечения 3-х графиков, их заносят в
Ответ: G min=8,665 при х=2,333 и y=1,333.
Область возможных решений
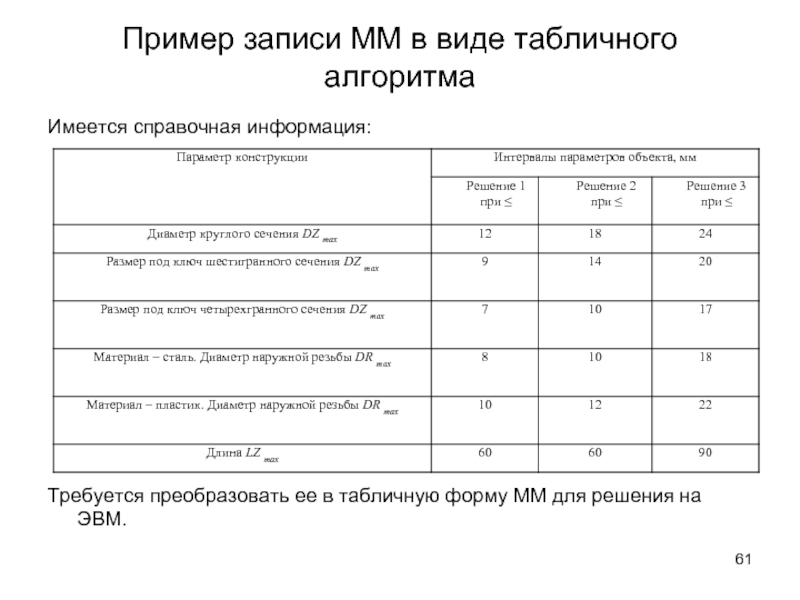
Слайд 61Пример записи ММ в виде табличного алгоритма
Имеется справочная информация:
Требуется преобразовать ее
Слайд 621. Составляется комплекс условий применимости (КУП) для принятия решения:
2. где М
Слайд 63Пример разработки ММ в аналитической форме и словесного алгоритма
Постановка задачи:
Кусок
Этап 1. Анализ требований. На рисунке представлен прямоугольник и его стороны: а – длина прямоугольника, b – ширина прямоугольника.
Периметр прямоугольника L=2a+2b
Площадь прямоугольника S=a⋅b, эта функция будет являться целевой функцией поиска значений параметров а и b.
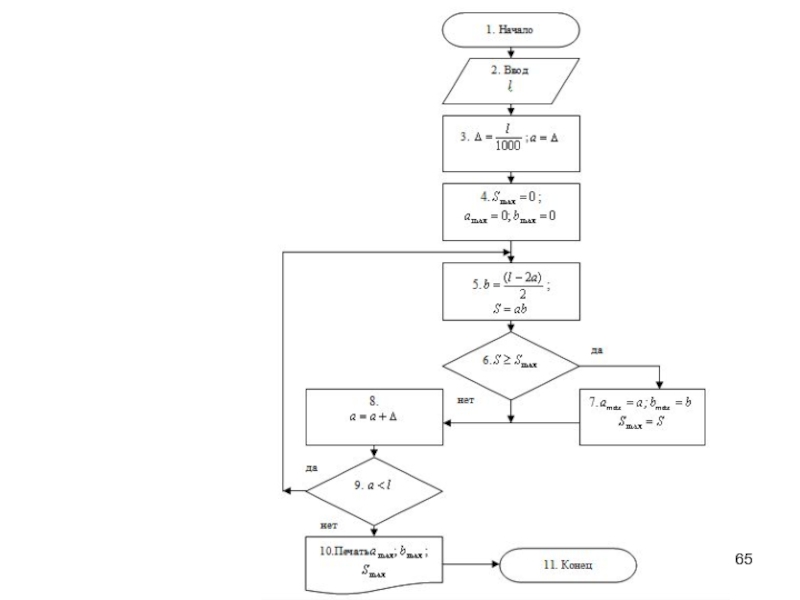
Слайд 64Пример разработки ММ в аналитической форме и словесного алгоритма
Этап 2. Разработка
Сформулируем словесный алгоритм:
Ввести значение L.
Вычислить Δ=L/1000.
Назначить a=Δ; S max =0; a max =0; b max =0;.
Вычислить b=(L−2a)/2.
Вычислить S= a ⋅ b.
Если S≥ S max, то a max =a; b max =b; S max =S.
Вычислить a=a+Δ.
Если a
Конец.
Слайд 67Этап 4. Расчет тестовых примеров. Тестовые примеры рассчитывают вручную и представляют в
Результат моделирования в EXCEL совпадает со значениями из тестового примера
Слайд 68Многокритериальные ММ
В предыдущих примерах мы рассматривали одну целевую функцию
Для реализации ММ на ЭВМ требуется множество целевых функции
свести к одной формуле. Например, аддитивный критерий объединяет (свертывает) несколько целевых функций в одну:
где λi − важность i -ой целевой функции для заказчика моделирования, выраженная в весовых коэффициентах; m − количество целевых функций.
Недостатки аддитивного критерия − субъективный подход к выбору весовых коэффициентов и все целевые функции должны стремиться либо к min, либо к max.
В случае, когда одни целевые функции стремятся к min, другие - к max, применяется минимаксный метод.
Слайд 69Комплексная целевая функция моделирования
где m – количество альтернативных вариантов решения; Pi,j
Каждый из параметров «стремится» к своему оптимальному значению opt.
Решение сводится к поиску наибольшего значения целевой функции F из m вариантов.
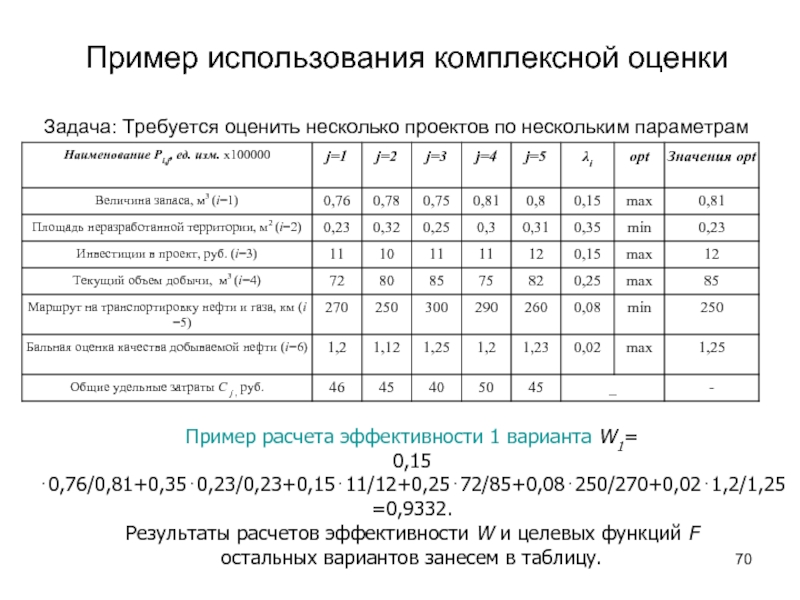
Слайд 70Пример использования комплексной оценки
Задача: Требуется оценить несколько проектов по нескольким параметрам
Пример
0,15⋅0,76/0,81+0,35⋅0,23/0,23+0,15⋅11/12+0,25⋅72/85+0,08⋅250/270+0,02⋅1,2/1,25
=0,9332.
Результаты расчетов эффективности W и целевых функций F
остальных вариантов занесем в таблицу.
Слайд 71Пример использования комплексной оценки
Результаты расчета
Для наглядности представления результатов моделирования строится
диаграмма
Вывод:
лучший – 3-й вариант,
так как значение
целевой функции
здесь достигает
максимума.
Слайд 72Спасибо за внимание ☺
Следующие занятия будут практическими.
1. Перед первым практическим
2. Скачайте файл «Перечень тем и заданий самостоятельной работы по ММ в расчетах на ЭВМ 2016»