- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Машина Тьюринга и ее устройство презентация
Содержание
- 1. Машина Тьюринга и ее устройство
- 2. Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический
- 3. 1) Внешний алфавит А = {a0,
- 4. 2) Внутренний алфавит Q = {q0,
- 5. 3) Внешняя память (лента) Машина имеет
- 6. 3) Внешняя память (лента) Устройство
- 7. 4) Каретка (управляющая головка) Каретка машины
- 8. 5) Функциональная схема (программа) Программа машины
- 9. Замечание 1) В недетерминированной машине может появиться
- 10. К началу работы машины на ленту
- 11. Описание работы машины Тьюринга Стандартное положение
- 12. Находясь в не заключительном состоянии, машина совершает
- 13. Описание работы машины Тьюринга В соответствии
- 14. При переходе машины в заключительное состояние q0
- 15. Машинным словом (конфигурацией) машины Тьюринга называется
- 16. Конфигурация α1qkal α2 интерпретируется следующим образом:
- 17. Пример Дана машина Тьюринга с внешним алфавитом
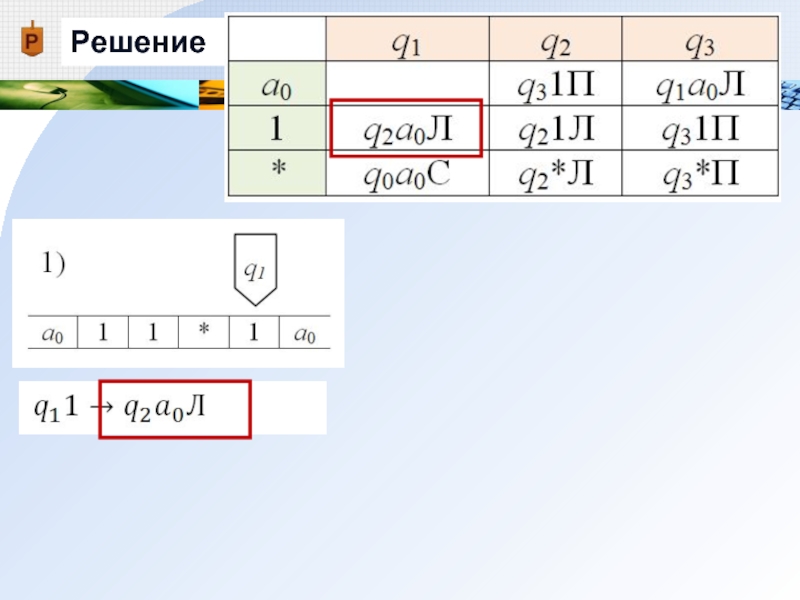
- 18. Решение
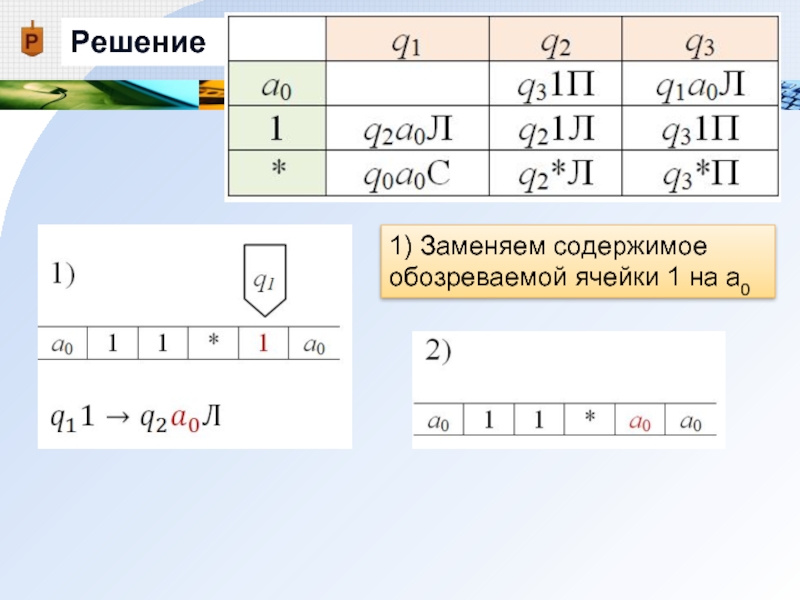
- 19. Решение 1) Заменяем содержимое обозреваемой ячейки 1 на а0
- 20. Решение 2) Машина переходит в новое состояние q2
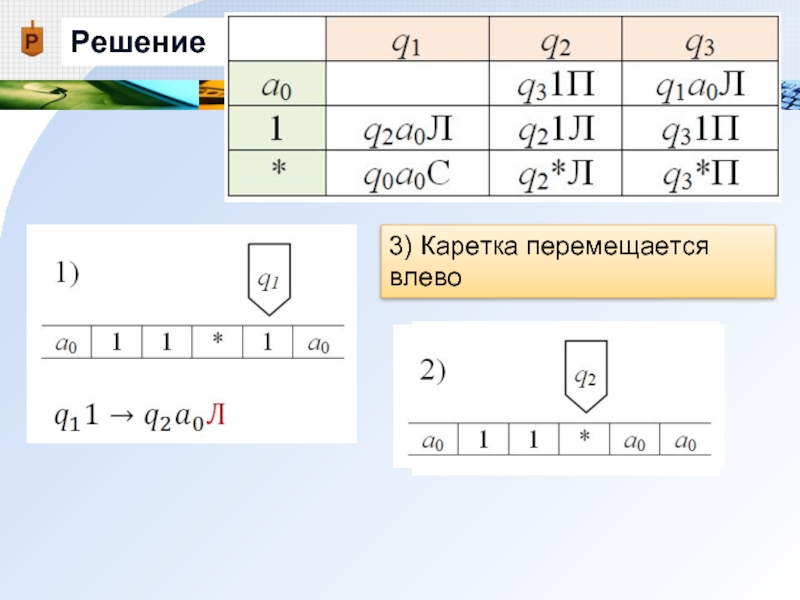
- 21. Решение 3) Каретка перемещается влево
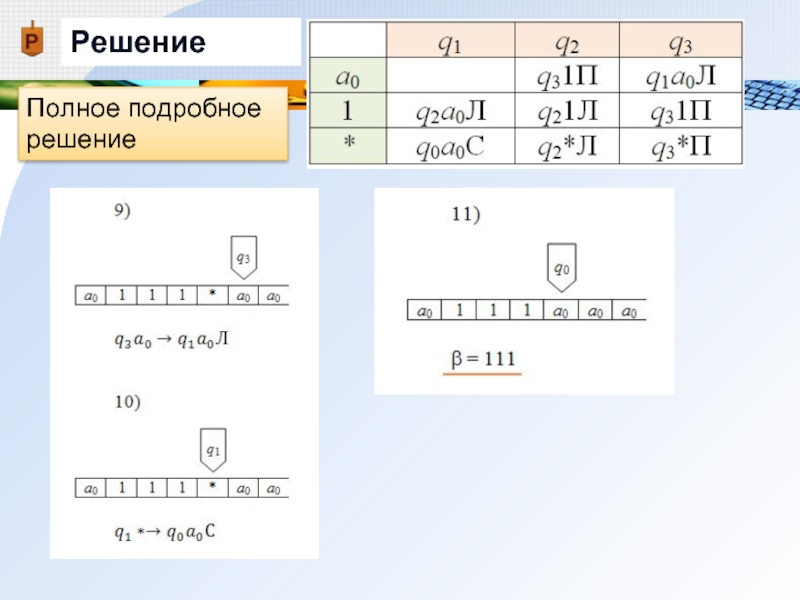
- 22. Решение Полное подробное решение
- 23. Решение Полное подробное решение
- 24. Решение Полное подробное решение
- 25. Решение Решение, записанное с помощью конфигураций (в строчку)
- 26. α = 1*11 Ответ: β = 111
- 27. Литература Игошин В.И. Математическая логика и теория
- 28. Люди могут вести себя по-разному в
Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический процесс Это математический объект, а не физическая машина Предложена Аланом Тьюрингом в 1936 году
Слайд 2Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический процесс
Это математический объект, а
не физическая машина
Предложена Аланом Тьюрингом в 1936 году
Предложена Аланом Тьюрингом в 1936 году
Слайд 3
1) Внешний алфавит
А = {a0, a1, …, an}
Элемент a0 называется пустой
символ
В этом алфавите в виде слова кодируется исходный набор данных и результат работы алгоритма
В этом алфавите в виде слова кодируется исходный набор данных и результат работы алгоритма
Устройство машины Тьюринга
Слайд 4
2) Внутренний алфавит
Q = {q0, q1, …, qm}, {П, Л, С}
В
любой момент времени машина М находится в одном из состояний q0, q1, …, qm
При этом: q1 - начальное состояние
q0 - заключительное состояние
Символы {П, Л, С} – символы сдвига (вправо, влево, на месте)
При этом: q1 - начальное состояние
q0 - заключительное состояние
Символы {П, Л, С} – символы сдвига (вправо, влево, на месте)
Устройство машины Тьюринга
Слайд 5
3) Внешняя память (лента)
Машина имеет ленту, разбитую на ячейки, в каждую
из которых может быть записана только одна буква
Устройство машины Тьюринга
Слайд 6
3) Внешняя память (лента)
Устройство машины Тьюринга
Пустая клетка содержит a0.
В каждый
момент времени на ленте записано конечное число непустых букв
Лента является конечной, но дополняется в любой момент ячейками слева и справа для записи новых непустых символов.
Это соответствует принципу абстракции потенциальной осуществимости
Лента является конечной, но дополняется в любой момент ячейками слева и справа для записи новых непустых символов.
Это соответствует принципу абстракции потенциальной осуществимости
Слайд 7
4) Каретка (управляющая головка)
Каретка машины располагается над некоторой ячейкой ленты –
воспринимает символ, записанный в ячейке
В одном такте работы каретка сдвигается на одну ячейку (вправо, влево) или остается на месте
В одном такте работы каретка сдвигается на одну ячейку (вправо, влево) или остается на месте
Устройство машины Тьюринга
Слайд 8
5) Функциональная схема (программа)
Программа машины состоит из команд:
Устройство машины Тьюринга
Для каждой
пары (qi, aj) программа машины должна содержать одну команду (детерминированная машина Тьюринга)
Слайд 9Замечание
1) В недетерминированной машине может появиться несколько параллельных вычислительных процессов
2) Разные
машины Тьюринга отличаются своими программами
Для каждого алгоритма создается своя машина Тьюринга, точнее ее программа
Для каждого алгоритма создается своя машина Тьюринга, точнее ее программа
Слайд 10
К началу работы машины на ленту подается исходный набор данных в
виде слова α
Описание работы машины Тьюринга
Будем говорить, что непустое слово α в алфавите А\{a0} воспринимается машиной в стандартном положении, если:
- оно задано в последовательных ячейках ленты,
- все другие ячейки пусты,
- машина обозревает крайнюю правую ячейку из тех, в которых записано слово α
Слайд 11
Описание работы машины Тьюринга
Стандартное положение называется начальным (заключительным), если машина, воспринимающая
слово в стандартном положении, находится в начальном состоянии q1 (стоп-состоянии q0)
Слайд 12Находясь в не заключительном состоянии, машина совершает шаг, который определяется текущим
состоянием qi и обозреваемым символом aj
Описание работы машины Тьюринга
Слайд 13
Описание работы машины Тьюринга
В соответствии с командой qiaj → qkal Х
выполняются следующие действия:
1) Содержимое обозреваемой ячейки aj стирается и в нее записывается символ al (который может совпадать с aj)
2) Машина переходит в новое состояние qk (оно может совпадать с состоянием qi)
3) Каретка перемещается в соответствии с управляемым символом Х ∈ {П, Л, С}
Слайд 14При переходе машины в заключительное состояние q0 ее работа прекращается
На ленте
записан результат работы алгоритма – слово β в алфавите А\{a0}
Описание работы машины Тьюринга
Слайд 15
Машинным словом (конфигурацией) машины Тьюринга называется слово вида α1qkal α2, где
α1 и α2 - слова в алфавите А.
Слайд 16Конфигурация α1qkal α2 интерпретируется следующим образом:
- машина находится в состоянии qk
-
каретка обозревает на ленте символ al
- α1 и α2 – это содержимое ленты до и после символа al
- α1 и α2 – это содержимое ленты до и после символа al
Слайд 17Пример
Дана машина Тьюринга с внешним алфавитом А = {a0, 1, *
}, алфавитом внутренних состояний Q = {q0, q1, q2, q3}, и следующей функциональной схемой:
Применить машину Тьюринга к слову α=11*1, начиная со стандартного начального положения
Слайд 27Литература
Игошин В.И. Математическая логика и теория алгоритмов. – М.: Академия, 2008.
- 448 с.
Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. – СПб.: Лань, 1999. - 288 с.
Ильиных А.П. Теория алгоритмов. Учебное пособие. – Екатеринбург, 2006. - 149 с.
Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. – СПб.: Лань, 1999. - 288 с.
Ильиных А.П. Теория алгоритмов. Учебное пособие. – Екатеринбург, 2006. - 149 с.
Слайд 28
Люди могут вести себя по-разному в одинаковых ситуациях, и этим они
принципиально отличаются от машин.
