- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические основы построения компьютера презентация
Содержание
- 1. Логические основы построения компьютера
- 2. История развития алгебры логики В 1842 году
- 3. «LOGOS» -- СЛОВО, МЫСЛЬ, ПОНЯТИЕ, РАССУЖДЕНИЕ, ЗАКОН
- 4. ОСНОВНЫЕ ФОРМЫ МЫШЛЕНИЯ Понятие Высказывание (Суждение, утверждение) Умозаключение
- 5. Понятие Понятие – это форма мышления, фиксирующая
- 6. ВЫСКАЗЫВАНИЕ Высказывание – это форма мышления, в
- 7. Примеры высказываний Ложь Истина Истина Ложь Истина
- 8. может быть простым и сложным
- 9. УМОЗАКЛЮЧЕНИЕ Умозаключение – это форма мышления, с
- 10. Алгебра высказываний
- 11. Алгебра высказываний была разработана для того, чтобы
- 12. Высказывание может принимать одно из двух возможных
- 13. Простые высказывания в алгебре логики обозначаются прописными
- 14. Составное высказывание на естественном языке образуется с
- 15. Логические операции
- 16. Инверсия - логическое отрицание Логическое отрицание
- 17. Операция И - логическое умножение (конъюнкция)
- 18. Операция ИЛИ - логическое сложение (дизъюнкция, объединение)
- 19. Импликация - логическое следование Результат операции следования
- 20. Операция «А тогда и только тогда, когда
- 21. Порядок выполнения логических операций Действия
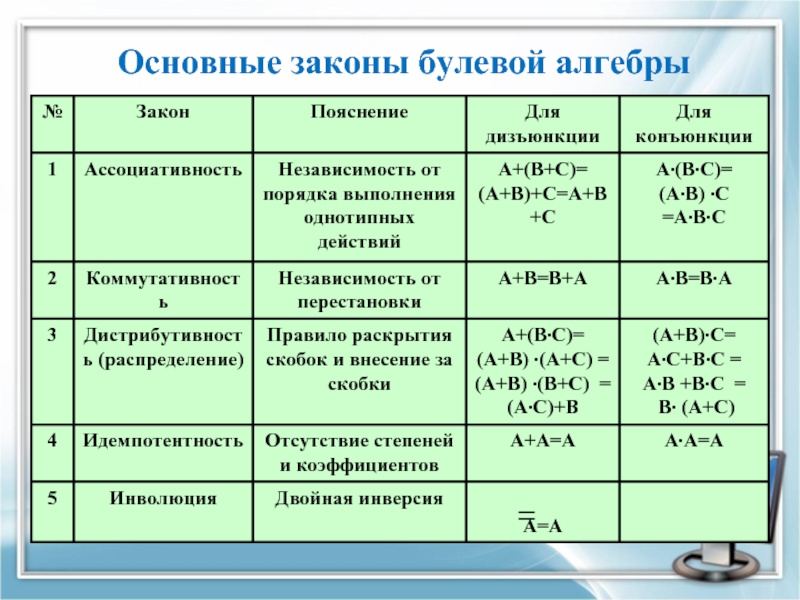
- 22. Основные законы булевой алгебры
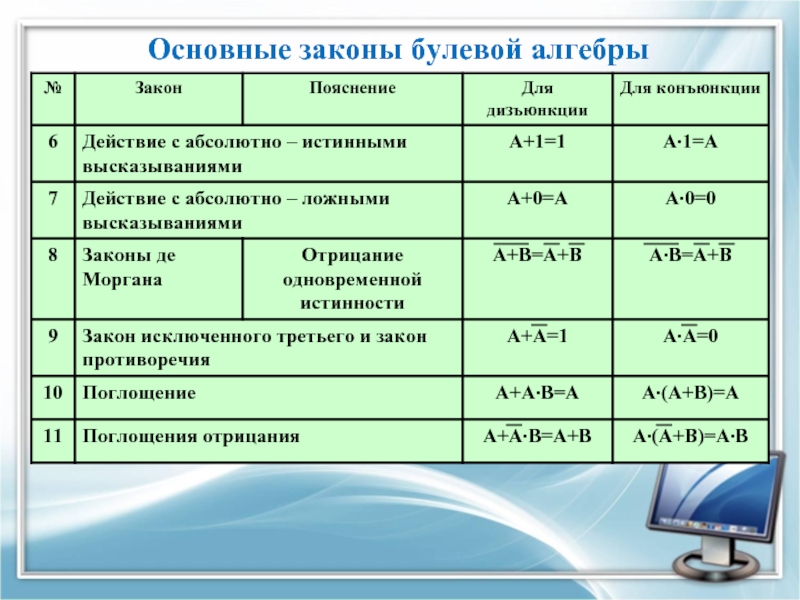
- 23. Основные законы булевой алгебры
- 24. РЕШЕНИЕ ЗАДАЧ
- 25. Задача. Формулой логического высказывания: «Если Катя
- 26. Составление таблиц истинности по логической формуле
- 27. Составление таблиц истинности по логической формуле
- 28. Задача. " Кто преступник"
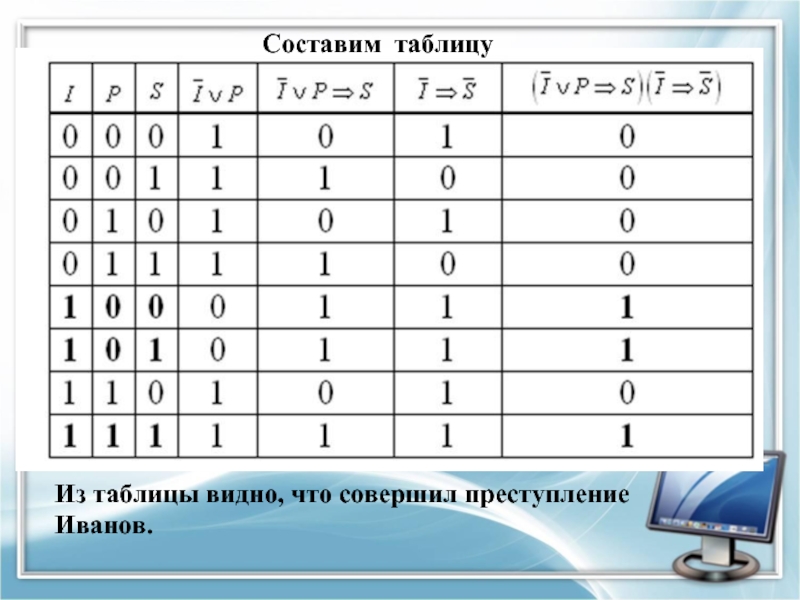
- 29. Из таблицы видно, что совершил преступление Иванов. Составим таблицу
- 30. Применим для решения этой же задачи преобразования
Слайд 2История развития алгебры логики
В 1842 году английский математик Джорж Буль разработал
Джорж Буль
2 .11.1815г. -8.12.1864 г.
Слайд 3«LOGOS» -- СЛОВО, МЫСЛЬ, ПОНЯТИЕ, РАССУЖДЕНИЕ, ЗАКОН
ЛОГИКА -- ЭТО УЧЕНИЕ О
Слайд 5Понятие
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
Например: компьютер,
Понятие
Содержание
Объем
Совокупность существенных признаков объекта
Например: содержание понятия ПК – универсальное электронное устройство для автоматической обработки информации
Совокупность предметов, на которую распространяется понятие
Например: понятие город – это множество городов;
Понятие ПК – совокупность существующих в мире ПК
Слайд 6ВЫСКАЗЫВАНИЕ
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается
Высказывание является повествовательным предложением.
Высказывание
Истинное
Ложное
Вопросительные и восклицательные предложения не являются высказываниями, так как в них ни чего не утверждается и не отрицается.
Слайд 7Примеры высказываний
Ложь
Истина
Истина
Ложь
Истина
Выражения, не являющиеся высказываниями
Не высказывание
Не высказывание
Не высказывание
Не высказывание
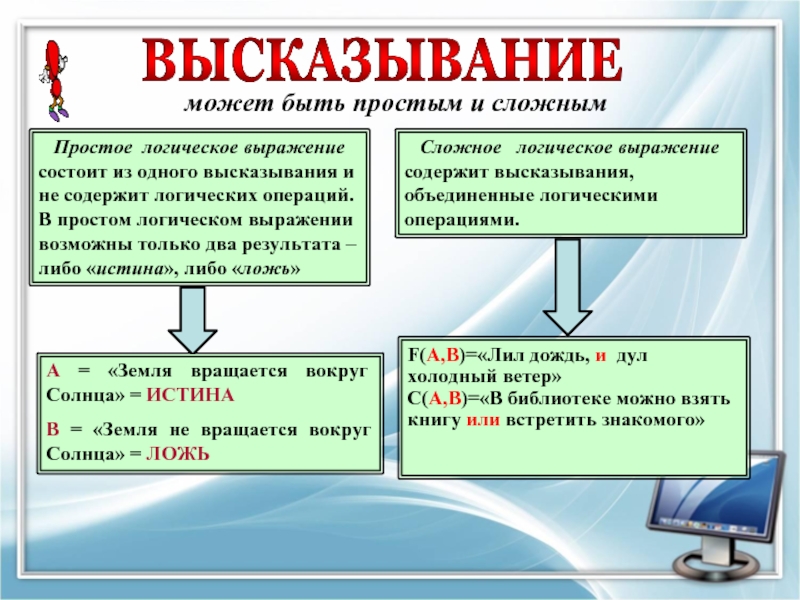
Слайд 8 может быть простым и сложным
Простое логическое выражение
состоит
А = «Земля вращается вокруг Солнца» = ИСТИНА
В = «Земля не вращается вокруг Солнца» = ЛОЖЬ
Сложное логическое выражение
содержит высказывания, объединенные логическими операциями.
F(A,B)=«Лил дождь, и дул холодный ветер»
С(A,B)=«В библиотеке можно взять книгу или встретить знакомого»
Слайд 9УМОЗАКЛЮЧЕНИЕ
Умозаключение – это форма мышления, с помощью которой из одного или
Посылками умозаключения – могут быть только
истинные суждения.
Например:
Слайд 11Алгебра высказываний была разработана для того, чтобы можно было определять истинность
Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно или ложно.
Слайд 12Высказывание может принимать одно из двух возможных логических значений:
ИСТИНА
ЛОЖЬ
ЛОГИЧЕСКИЕ ПОСТОЯННЫЕ
Или
ЛОГИЧЕСКИЕ КОНСТАНТЫ
1
0
Слайд 13Простые высказывания в алгебре логики обозначаются прописными латинскими буквами.
А – «Два
В – «Два умножить на два равно пяти».
Какова истинность высказываний?
Первое высказывание истинно (А = 1).
Второе высказывание ложно (В = 0).
Слайд 14Составное высказывание на естественном языке образуется с помощью связок и, или,
которые в алгебре логики заменяются на логические операции умножения, сложения и отрицания.
Логические операции задаются таблицами истинности.
Слайд 16
Инверсия - логическое отрицание
Логическое отрицание делает истинное высказывание ложным и, наоборот,
Таблица истинности функции логического отрицания
Пример: Даны высказывания
А – «Число 4 – четное» = ИСТИНА
Не А – «Неверно, что число 4 – четное» = ЛОЖЬ
В переводе на естественный язык «Не А», «Неверно, что А»
ИСТИНА – 1 ЛОЖЬ - 0
или
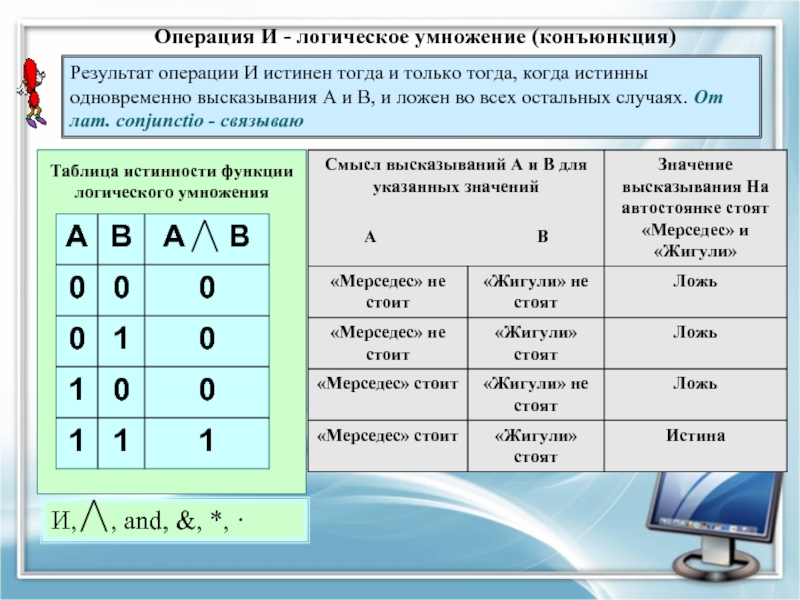
Слайд 17Операция И - логическое умножение (конъюнкция)
Таблица истинности функции логического умножения
И,
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях. От лат. conjunctio - связываю
Слайд 18Операция ИЛИ - логическое сложение (дизъюнкция, объединение)
Таблица истинности функции логического сложения
ИЛИ,
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложно тогда, когда аргументы А и В –ложны От лат. disjunctio – различаю.
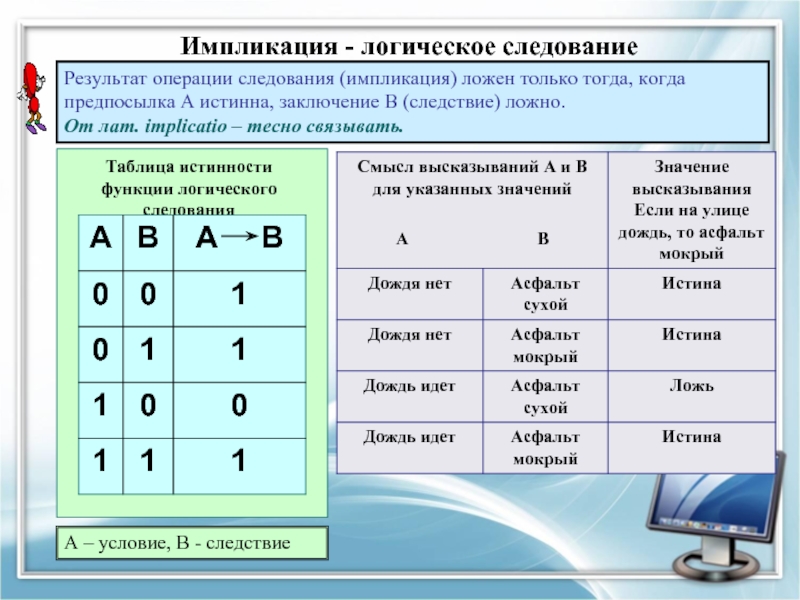
Слайд 19Импликация - логическое следование
Результат операции следования (импликация) ложен только тогда, когда
Таблица истинности функции логического следования
А – условие, В - следствие
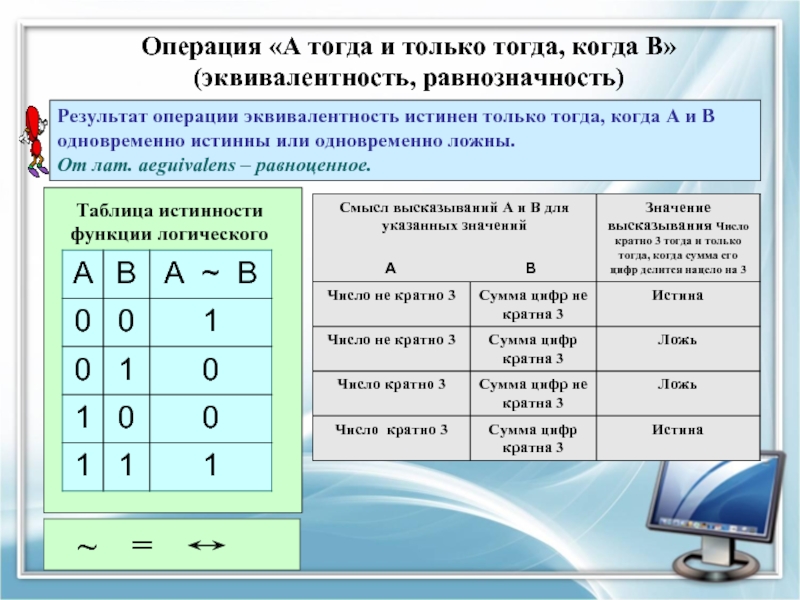
Слайд 20Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
Результат операции
Таблица истинности функции логического равенства
~ =
Слайд 21Порядок выполнения логических операций
Действия в скобках.
Операция отрицания (“не”).
Конъюнкция (“и”).
Дизъюнкция (“или”).
Эквивалентность .
Слайд 25Задача. Формулой логического высказывания:
«Если Катя окончит четверть без «троек» и
А => (В & С);
(А│В) &С;
(A&B) =>C;
(A=> B)&C.
ОТВЕТ: (A&B) =>C.
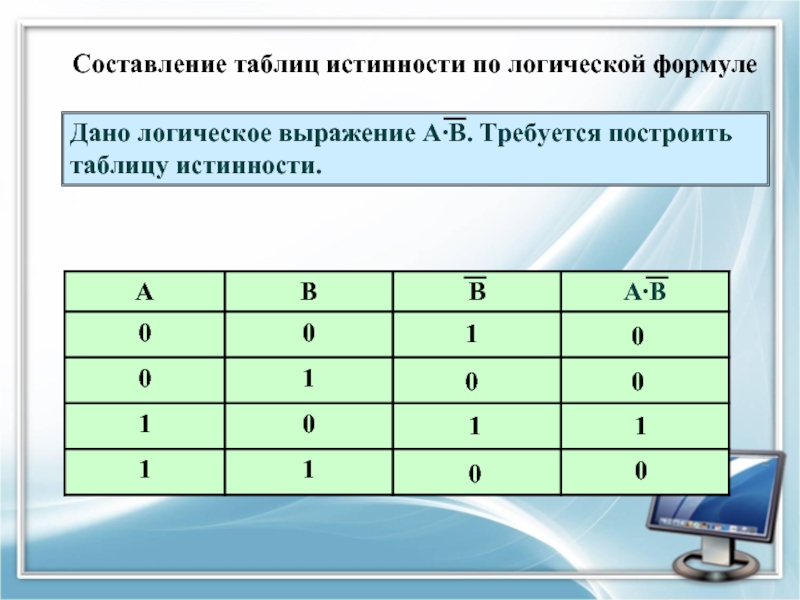
Слайд 26Составление таблиц истинности по логической формуле
Дано логическое выражение А∙В. Требуется
1
0
1
0
0
0
1
0
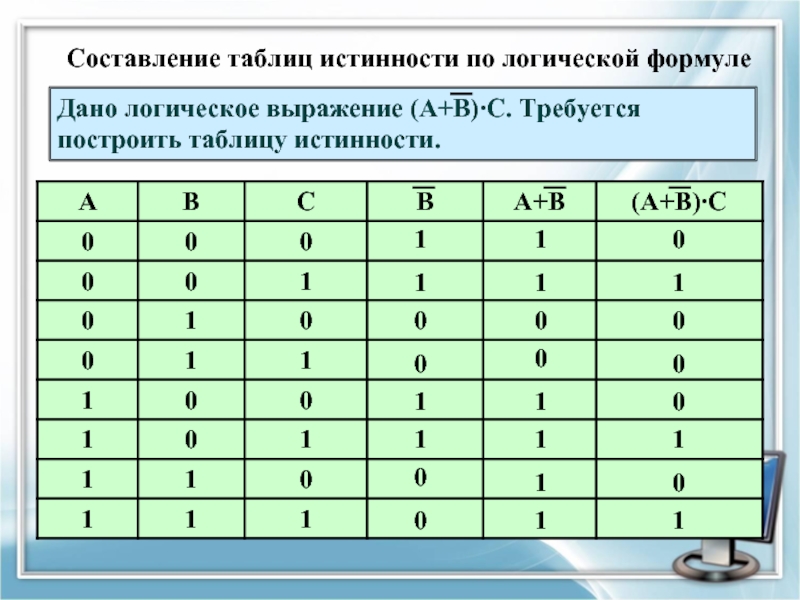
Слайд 27Составление таблиц истинности по логической формуле
Дано логическое выражение (А+В)∙С. Требуется
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
1
0
1
0
0
0
1
0
1
Слайд 28 Задача. " Кто преступник"
Определить участника преступления, исходя
1) "Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал";
2) "Если Иванов не участвовал, то Сидоров не участвовал".
Решение
Составим выражения:
I - "Иванов участвовал в преступлении";
P - "Петров участвовал в преступлении";
S - "Сидоров участвовал в преступлении".
Запишем посылки в виде формул:
¬I˅P→S и ¬I→¬S
Слайд 30Применим для решения этой же задачи преобразования с помощью законов
Тогда имеем:
F(I,P,S)=( ¬I˅P→S) &( ¬I→¬S)=(¬(¬I˅P)˅S) & (I˅¬S) =
= (I & ¬P ˅S) & (I ˅¬S) = I&¬P˅ I & S˅ I &¬P &¬S ˅0 = = I&¬P ˅ I & S = I & (¬P˅S)
Из последнего выражения видно, что выражение верно, если I=1, значит преступник - Иванов.