- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические основы ЭВМ презентация
Содержание
- 1. Логические основы ЭВМ
- 2. Алгебра логики – это раздел
- 3. Алгебра высказываний Алгебра высказываний была разработана для
- 4. Основными элементами логики высказываний являются логическая переменная
- 5. Логические переменные Логические переменные–
- 6. СПОСОБЫ ЗАПИСИ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ Истина
- 7. «2 × 2 = 4» истина (1)
- 8. В алгебре высказываний высказывания обозначаются именами логических
- 9. В алгебре высказываний над логическими переменными (над
- 10. Составные высказывания Высказывания, состоящие из нескольких простых
- 11. Каждое составное высказывание можно выразить в
- 12. ЛОГИЧЕСКАЯ ОПЕРАЦИЯ
- 13. Объединение двух или нескольких высказываний в одно
- 14. Запись конъюнкции на формальном языке алгебры высказываний
- 15. Логическая функция, полученная в результате конъюнкции, истинна
- 16. Конъюнкция. Определите истинность логической функции «2
- 17. Значение логической функции определяется по
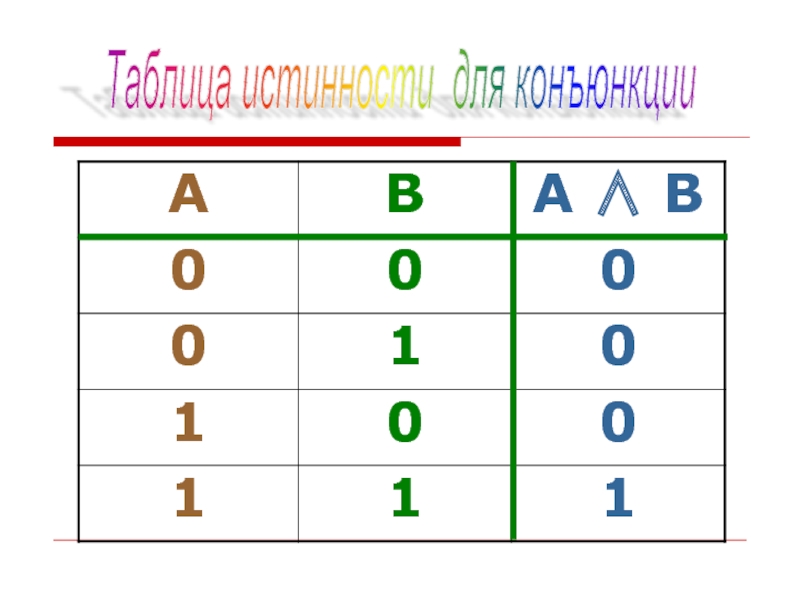
- 18. Таблица истинности для конъюнкции
- 19. Таблица истинности для конъюнкции
- 20. Объединение двух или нескольких высказываний в одно
- 21. Запись дизъюнкции на формальном языке алгебры
- 22. Логическая функция, полученная в результате дизъюнкции, истинна
- 23. Дизъюнкция. Определите истинность логической функции «2
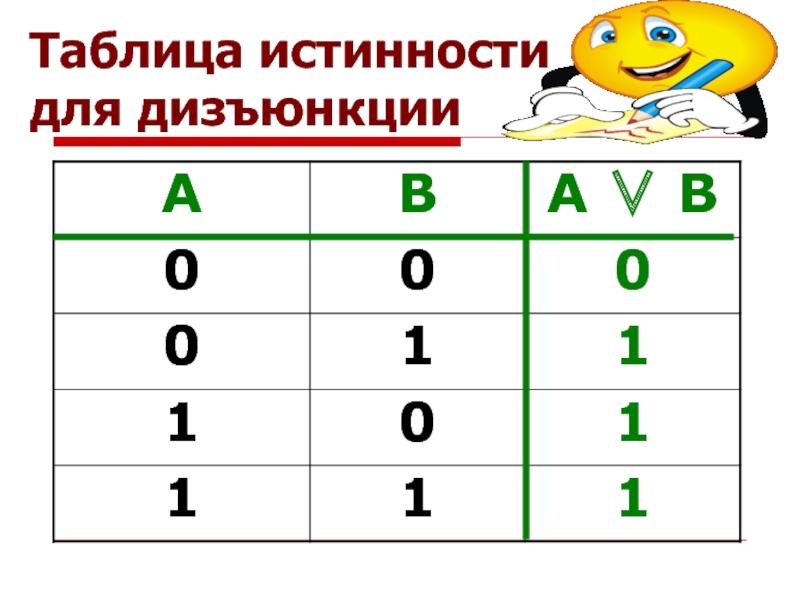
- 24. Таблица истинности для дизъюнкции
- 25. Таблица истинности для дизъюнкции
- 26. Присоединение частицы «НЕ» к высказыванию называется операцией
- 27. Запись инверсии на формальном языке алгебры высказываний
- 28. Логическое отрицание (инверсия) делает истинное высказывание ложным,
- 29. Инверсия Пусть A = «2 ×
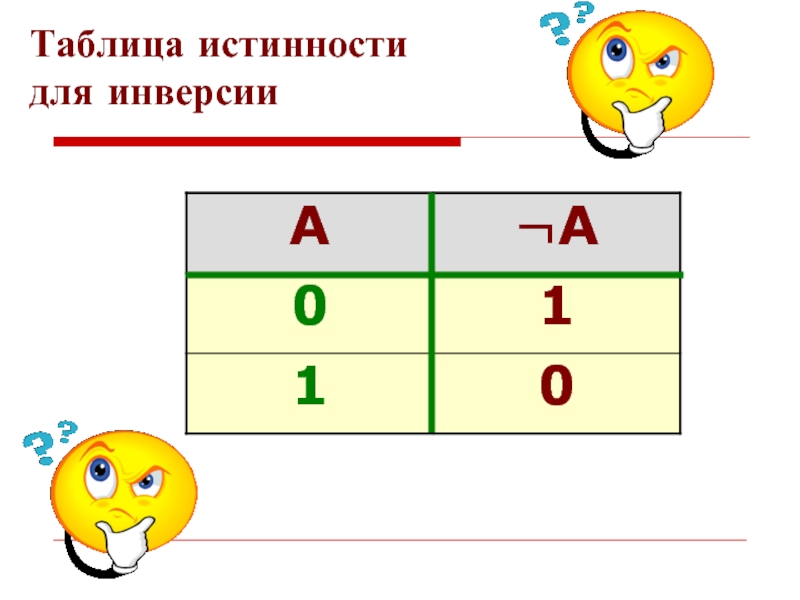
- 30. Таблица истинности для инверсии
- 31. Дополнительные логические функции Импликацию и
- 32. Объединение двух высказываний, из которых первое является
- 33. Импликация ложна тогда и только тогда,
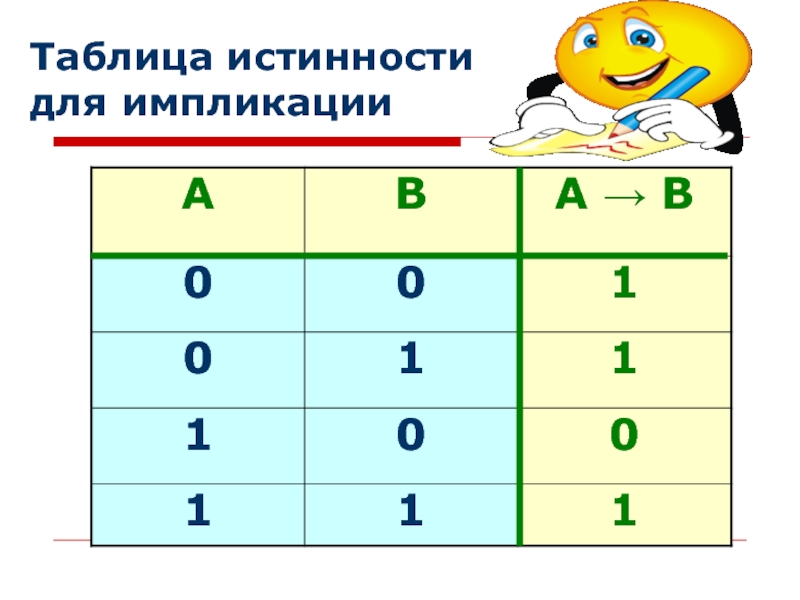
- 34. Таблица истинности для импликации
- 35. Эквивалентность Эквивалентность (равнозначность)– это логическая операция, объединяющая
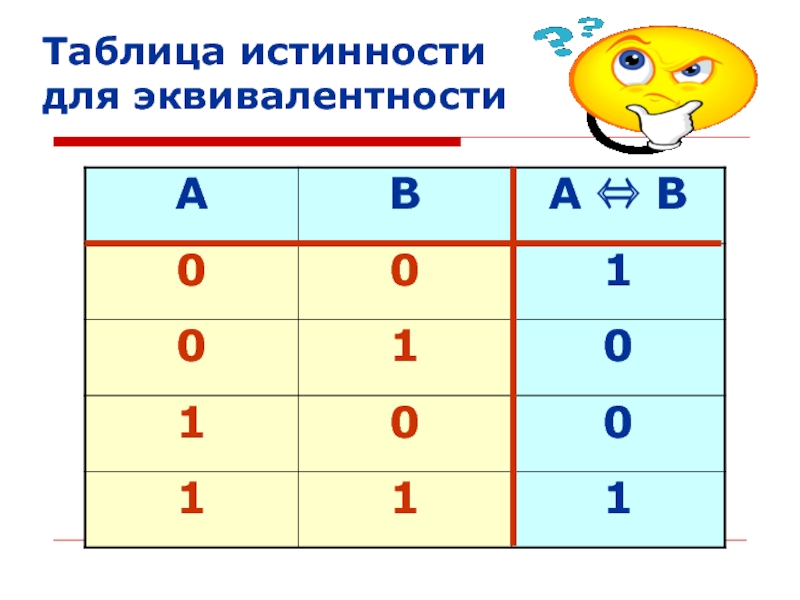
- 36. Таблица истинности для эквивалентности
- 37. ЗАКРЕПЛЕНИЕ ПРИВЕДИТЕ ПРИМЕРЫ КОНЪЮНКЦИИ Приведите примеры
- 38. ЗАДАНИЯ Найдите правильно построенное отрицание
- 39. Запишите схематически следующие высказывания Быть иль
- 40. НА ДОМ: КОНСПЕКТ Формула Высказывание
Слайд 1Логические основы ЭВМ
СОДЕРЖАНИЕ
Алгебра высказываний
Логические переменные
Логические функции
4. Логические операции
5. Виды
6. Таблица истинности функций
Слайд 2
Алгебра логики – это раздел математики, изучающий сложные высказывания, рассматриваемые со
Алгебра логики возникла в середине 19 века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Слайд 3Алгебра высказываний
Алгебра высказываний была разработана для того, чтобы определять истинность или
Слайд 4Основными элементами логики высказываний являются логическая переменная и логическая формула Некоторые
Для таких действий, для изменения изначального выражения без внесения изменений в результат, используют тождественно истинные высказывания.
ОСНОВЫ ЛОГИКИ
Слайд 5Логические
переменные
Логические переменные– простые высказывания, содержащие только одну мысль.
Обозначаются буквами латинского алфавита: A, B, C…
Логические переменные могут принимать лишь два значения: «ИСТИНА» (1) или «ЛОЖЬ» (0)
Слайд 7
«2 × 2 = 4» истина (1)
Например, два простых высказывания:
являются логическими переменными
«2
А
и В
А =
В =
Слайд 8В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать
ВЫВОД
Слайд 9В алгебре высказываний над логическими переменными (над высказываниями) можно производить определенные
Слайд 10Составные высказывания
Высказывания, состоящие из нескольких простых суждений и содержащие в себе
Обозначаются F(A,B,C…)
Также могут принимать значения «ИСТИНА» или «ЛОЖЬ» в зависимости от того, какие значения имеют входящие в их состав логические переменные и от действий над ними
Слайд 11
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в
Для записи составного высказывания в виде логического выражения на формальном языке в составном высказывании нужно выделить простые высказывания и логические связи между ними.
запишем в форме логического выражения составное высказывание "(2*2=5 или 2*2=4) и (2*2 5 или 2*2 4)".Проанализируем составное высказывание. Оно содержит два простых высказывания:
А= "2*2=5" - ложно (0)
В= "2*2=4" - истинно (1)
Тогда составное высказывание можно записать в следующей форме: "(А или В) и ( А или В)".
Слайд 12 ЛОГИЧЕСКАЯ ОПЕРАЦИЯ
способ построения сложного высказывания из
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция
Слайд 13Объединение двух или нескольких высказываний в одно с помощью союза «И»
КОНЪЮНКЦИЯ
Слайд 14Запись конъюнкции на формальном языке алгебры высказываний
F(A,B) = A & B
или
F(A,B) = A ∧ B
Также может встретиться запись, типа:
F(A,B) = A * B
или
F(A,B) = A and B
Слайд 15Логическая функция, полученная в результате конъюнкции, истинна тогда и только тогда,
F(A,B) = A ∧ B
Слайд 16Конъюнкция. Определите истинность логической функции
«2 × 2 = 5» И «3
«2 × 2 = 5» И «3 × 3 = 9»
«2 × 2 = 4» И «3 × 3 = 10»
«2 × 2 = 4» И «3 × 3 = 9»
Истинна только функция (4)
Слайд 17Значение логической
функции определяется
по ее таблице истинности
Таблица истинности показывает какие
Слайд 20Объединение двух или нескольких высказываний в одно с помощью союза «ИЛИ»
ДИЗЪЮНКЦИЯ
Слайд 21Запись дизъюнкции на формальном языке
алгебры высказываний
F(A,B) = A ∨ B
Также может встретиться запись, типа:
F(A,B) = A + B
или
F(A,B) = A or B
Слайд 22Логическая функция, полученная в результате дизъюнкции, истинна тогда, когда истинна хотя
F(A,B) = A ∨ B
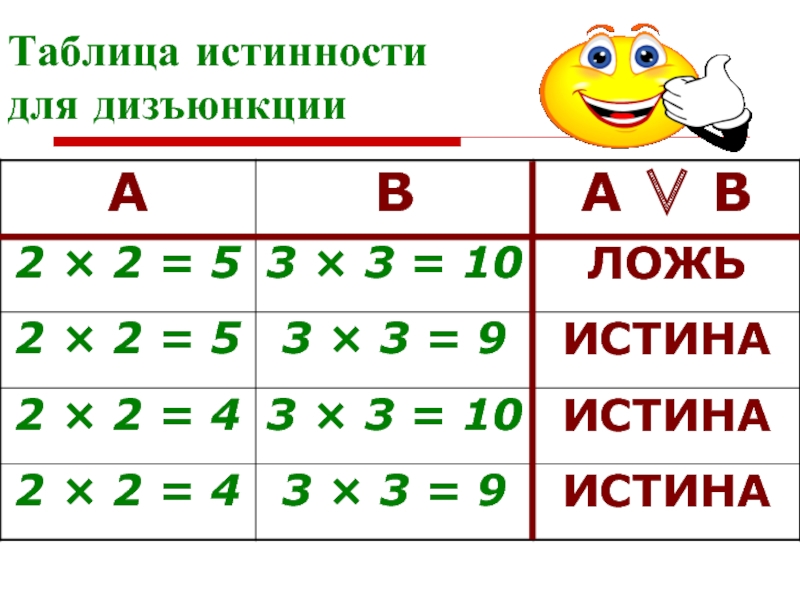
Слайд 23Дизъюнкция. Определите истинность логической функции
«2 × 2 = 5» ИЛИ «3
«2 × 2 = 5» ИЛИ «3 × 3 = 9»
«2 × 2 = 4» ИЛИ «3 × 3 = 10»
«2 × 2 = 4» ИЛИ «3 × 3 = 9»
Ложна только функция
(1), остальные истинны
Слайд 26Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания, или инверсией
И
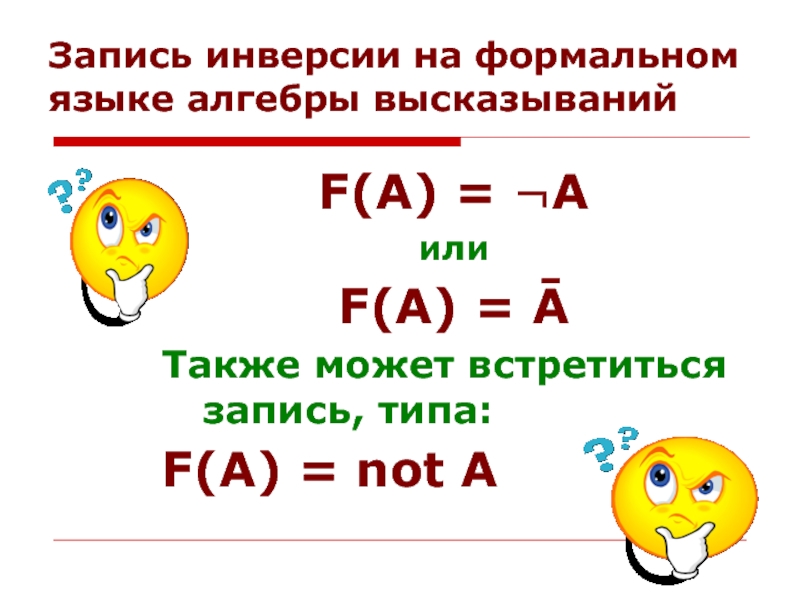
Слайд 27Запись инверсии на формальном языке алгебры высказываний
F(A) = ¬A
или
F(A) = Ā
Также
F(A) = not А
Слайд 28Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным
F(A) = Ā
Слайд 29Инверсия
Пусть
A = «2 × 2 = 4»
– истинное высказывание, тогда
F(A)
– ложное высказывание
Слайд 31Дополнительные
логические функции
Импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию
Импликация:
А → В = ¬A ∨ В или
А ⊃ В = ¬A ∨ В или
А ⇒ В = ¬A ∨ В
Эквивалентность:
А ↔ В = (¬A ∨ В) ∧ (¬B ∨ A) или
А ⇔ В = (¬A ∨ В) ∧ (¬B ∨ A) или
А ≡ В = (¬A ∨ В) ∧ (¬B ∨ A)
Слайд 32Объединение двух высказываний, из которых первое является условием, а второе –
Импликация
Слайд 33Импликация ложна тогда и только тогда, когда условие истинно, а следствие
Пример:
Если выучишь материал, то сдашь зачет
Это высказывание ложно только тогда, когда материал выучен, а зачет не сдан, т.к. сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой
Импликация
A => B
Слайд 35Эквивалентность
Эквивалентность (равнозначность)– это логическая операция, объединяющая два простых высказывания в одно
<=>
A
B
Слайд 37ЗАКРЕПЛЕНИЕ
ПРИВЕДИТЕ ПРИМЕРЫ КОНЪЮНКЦИИ
Приведите примеры истинной и ложной конъюнкции двух или
Приведите примеры истинной и ложной дизъюнкции двух или нескольких высказываний.
Как в русском языке может обозначаться дизъюнкция?
Слайд 38ЗАДАНИЯ
Найдите правильно построенное отрицание суждения "Все воздушные шары зелёные":
Все воздушные
Не верно, что все воздушные шары зелёные.
Докажите свою точку зрения с помощью определения. Запишите отрицания следующих высказываний:
Сегодня хорошая погода.
Число 3 - чётное.
Некоторые млекопитающие не живут на суше.
Во всякой школе некоторые ученики увлекаются программированием.
Слайд 39Запишите схематически следующие высказывания
Быть иль не быть - вот в
"Если хочешь быть красивым, поступи в гусары." (К. Прутков)
Ядерная энергия - это не электричество, не тяготение, просто химия - словом, неизвестно что.
Если краткость - сестра таланта, то сокращение - дитя гения.
А V Ā <=> В
А => В
А <=> B v C < = > D v P
А => В
Слайд 40НА ДОМ:
КОНСПЕКТ
Формула Высказывание Тигр Волк Бурундук Заяц Медведь
В Зверь хищный
не A
не B
A и B
A или B
Заполнить таблицу